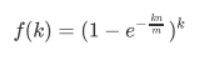判断值存在 - 布隆过滤器Bloom Filter
- 业务场景:大量数据判断单值是否存在,且大量数据远远超出服务器的内存,无法使用HashMap,因为HashMap的时间复杂度虽然为O(1),但是其数据都是在内存中的。
1、布隆过滤器数据结构
一种占比空间很小、空间效率很高的随机数据结构,有一个很长的二进制向量和一组Hash映射函数组成。
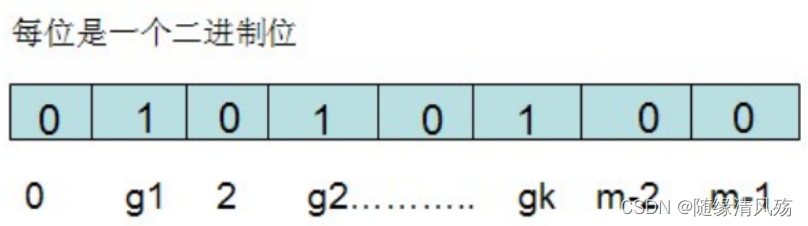
- 一个大型位数组(二进制数组)
- 多个Hash映射函数:元素的hash值均匀映射到位数组中
2、实现原理
(1)初始状态
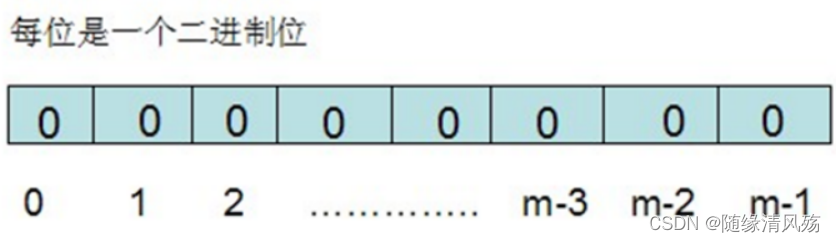
布隆过滤器需要的是一个位数组和K个映射函数,在初始状态时,对于长度为m的位数组array,他的所有位被置0。
(2)数据插入
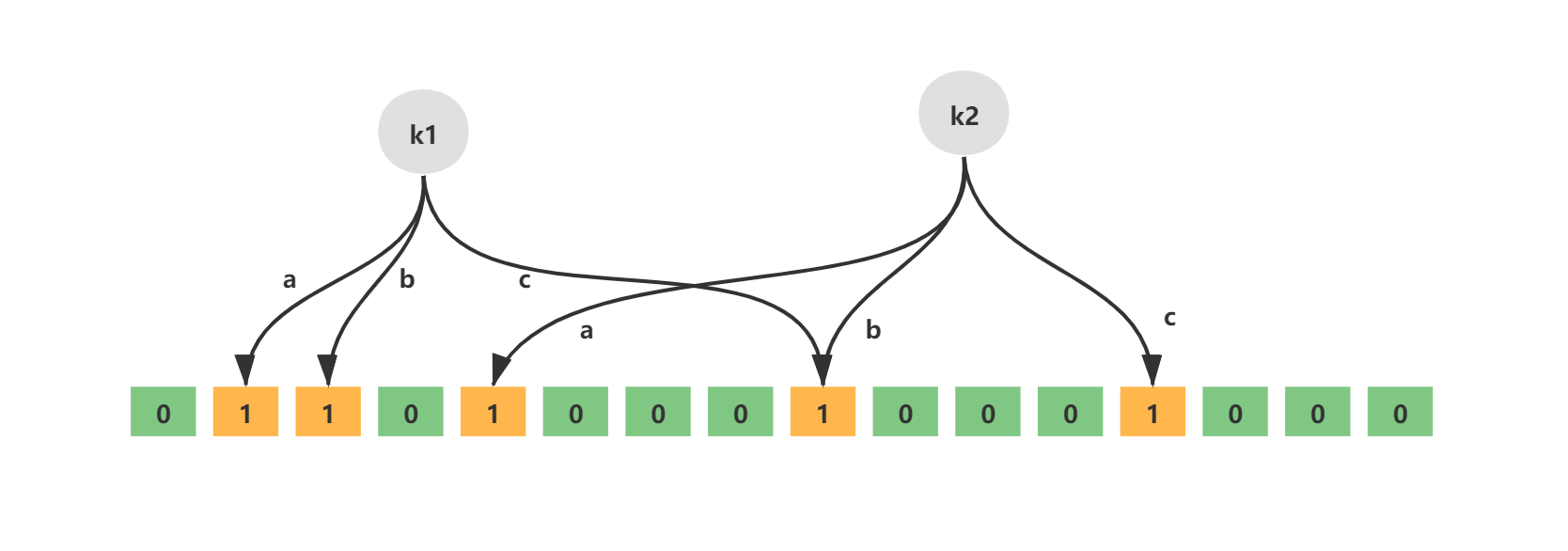
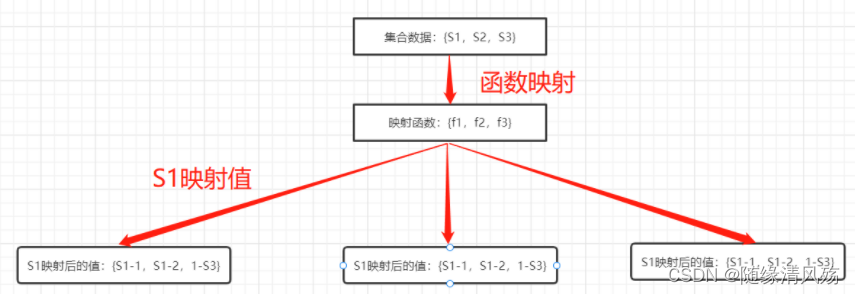
对于有n个元素的集合S={S1,S2…Sn},通过k个映射函数{f1,f2…fk},将集合中的每个元素都映射为K个值{g1,g2…gk},然后再将数组array中相对应的array[g1],array[g2]…array[gk]置为1
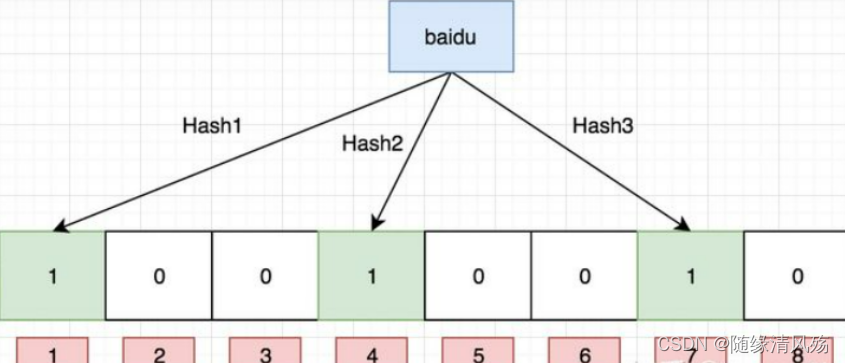
- 插入案例1:“baidu” 和三个不同的哈希函数分别生成了哈希值 1、4、7。
- 插入案例2:“tencent” 和三个不同的哈希函数分别生成了哈希值 3、4、8。
(3)数据查找
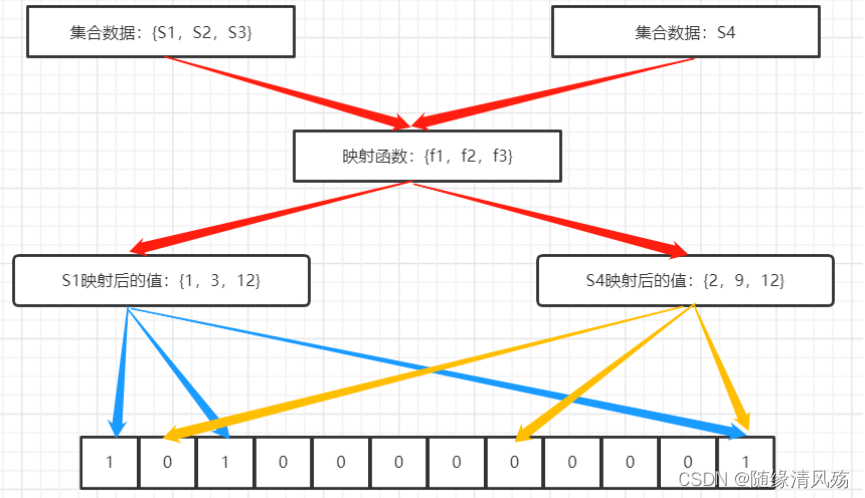
要查找某个元素item是否在S中,则通过映射函数{f1,f2,…fk}得到k个值{g1,g2…gk},然后再判断 array[g1],array[g2]…array[gk]是否都为1,若全为1,则item在S中,否则item不在S中。这个就是布隆 过滤器的实现原理。
S1的Hash查找结果:1,3,12 位数组中都有相关值,则判定存在
S4的Hash查找结果:2,9,12 为数组中只有一个存在,则判定不存在
1.3、布隆过滤器优缺点
(1)优点
①远远缩小存储空间的数据规模
-
布隆过滤器不需要存储元素本身;
-
布隆过滤器可以表示全集,其他任何数据结构都不能。
②能快速判断元素存在不存在
- Hash函数相互之间没有关系,方便由硬件并行执行;
- k和m相同,使用同一组Hash函数的两个布隆过滤器的交并差运算可以使用位操作进行。
(2)缺点
①有一定误判率
- 本质上是由Hash冲突引起的,原本不存在于该集合的元素,布隆过滤器有可能会判断说它存在,但是如果布隆过滤器判断某一个元素不存在该集合,那么该元素一定不在该集合内。
②不支持删除操作
- 删除元素首先确保元素的确在布隆过滤器里面,但是布隆过滤器无法保证
1.4、误判率估计
误判本质上是Hash冲突导致的,布隆过滤器解决哈希冲突的方法是多哈希法;
(1)多哈希法
设计二种甚至多种哈希函数,可以避免冲突,但是冲突几率还是有的,函数设计的越好或越多都可以将几率降到最低(除非人品太差,否则几乎不可能冲突)。
(2)误判率计算
- 业务场景
位数组大小:m
总共数据大小为:n
hash函数的个数为:k
①对某一特定bit位在一个元素,调用hash函数之后,其改成1的概率是
1
/
m
1/m
1/m
②对某一特定bit位在一个元素由单个hash函数没有置为1的概率
1
−
1
/
m
1-1/m
1−1/m
③对某一特定bit位在一个元素由k个hash函数没有置为1的概率
(
1
−
1
/
m
)
k
(1-1/m)^k
(1−1/m)k
④当n个数据插入进来,某一个bit位没有被置为1的概率
[
(
1
−
1
/
m
)
k
]
n
[(1-1/m)^k]^n
[(1−1/m)k]n
⑤当n个数据插入进来,某一个bit位被置为1的概率
1
−
[
(
1
−
1
/
m
)
k
]
n
1-[(1-1/m)^k]^n
1−[(1−1/m)k]n
⑥查询单个元素,则调用k个hash函数得到k个位置值,然后再去判断这k个位置值是不是1
计
算
出
来
的
k
个
位
置
值
都
是
1
的
概
率
=
[
1
−
[
(
1
−
1
/
m
)
k
]
n
]
k
计算出来的k个位置值都是1的概率 = [1-[(1-1/m)^k]^n]^k
计算出来的k个位置值都是1的概率=[1−[(1−1/m)k]n]k
-
总而言之:当m增大或者n减小时,都会使误差率减小
-
总结:
- 位数组长度:长度会直接影响误报率,布隆过滤器越长其误报率越高
- 哈希函数个数:个数越多则布隆过滤器bit位置变1的速度越快,且布隆过滤器的效率越低,个数太少,则误报率会变高。
1.5、最优哈希个数
对于给定的m和n时,k为何值时可以使误判率最低,设误判率的函数如下:
当m和n确定了以后,k为以下值时,误判率是最低的。
k
≈
0.7
∗
(
m
/
n
)
k≈0.7*(m/n)
k≈0.7∗(m/n)
- 总结:如想保持某固定误判率不变,布隆过滤器的bit数m和被add的元素数n应该是线性同步增加的。
1.6、布隆过滤器设计实战
(1)业务场景
有两个URL集合A,B,每个集合中大约有1亿个URL,每个URL占64字节,有1G的内存,如何找出两个集合中重复的URL。
(2)解决思路
①直接利用Hash表会超出内存限制的范围
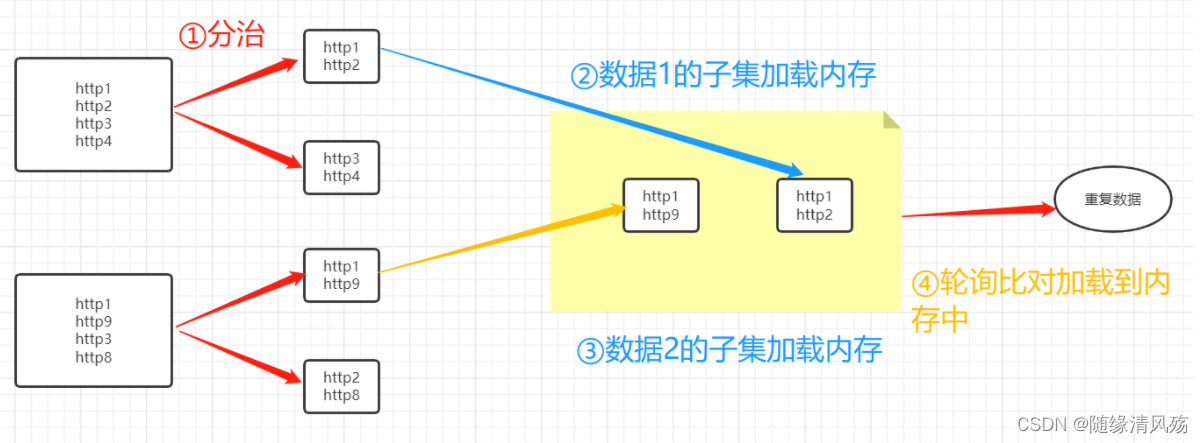
②如果不允许一定的错误率的话,则使用分治思想
将A,B两个集合中的URL分别存到若干个文件中{f1,f2…fk}和{g1,g2…gk}中,然后取f1和g1的内容读入内存,将f1的内容存储到hash_map当中,然后再取g1中的url,若有相同的url,则写入到文件中,然后直到g1的内容读取完毕,再取g2…gk。然后再取f2的内容读入内存…,依次类推,知道找出所有的重复url。
③如果允许有一定错误率的话,则可以使用布隆过滤器
public class MyBloomFilter {
// 位数组的大小
private final static int DEFAULT_CAPACITY = 2 << 22;
// 实现不同hash函数的参数数组
private final static int[] SEEDS = {3, 13, 46, 76, 91, 138};
// 定义位数组
private final BitSet bits = new BitSet(DEFAULT_CAPACITY);
// 存放哈希函数的类数组
private final SimpleHash[] func = new SimpleHash[SEEDS.length];
// 对哈希函数进行初始化
public MyBloomFilter() {
for (int i = 0; i < SEEDS.length; i++) {
func[i] = new SimpleHash(DEFAULT_CAPACITY, SEEDS[i]);
}
}
// 添加元素到位数组操作
public void add(Object value) {
for (int i = 0; i < SEEDS.length; i++) {
bits.set(func[i].hash(value), true);
}
}
// 判断是否存在操作
public boolean contains(Object value) {
boolean ret = true;
for (SimpleHash f : func) {
ret &= bits.get(f.hash(value));
}
return ret;
}
/*
静态内部类:用于实现不同的哈希函数
*/
private static class SimpleHash {
private final int cap;
private final int seed;
public SimpleHash(int cap, int seed) {
this.cap = cap;
this.seed = seed;
}
/**
* 计算哈希值
*/
public int hash(Object key) {
int h;
return (key == null) ? 0 : Math.abs(seed * (cap - 1) & ((h = key.hashCode()) ^ (h >>> 16)));
}
}
}