光流跟踪算法对车位进行跟踪
概念
光流是空间运动物体在观察成像平面上的像素运动的瞬时速度,是利用图像序列中像素在时间域上的变化以及相邻帧之间的相关性来找到上一帧跟当前帧之间存在的对应关系,从而计算出相邻帧之间物体的运动信息的一种方法。
一般而言,光流是由于场景中前景目标本身的移动、相机的运动,或者两者的共同运动所产生的。
- 当描述部分像素时,称为:稀疏光流
- 当描述全部像素时,称为:稠密光流
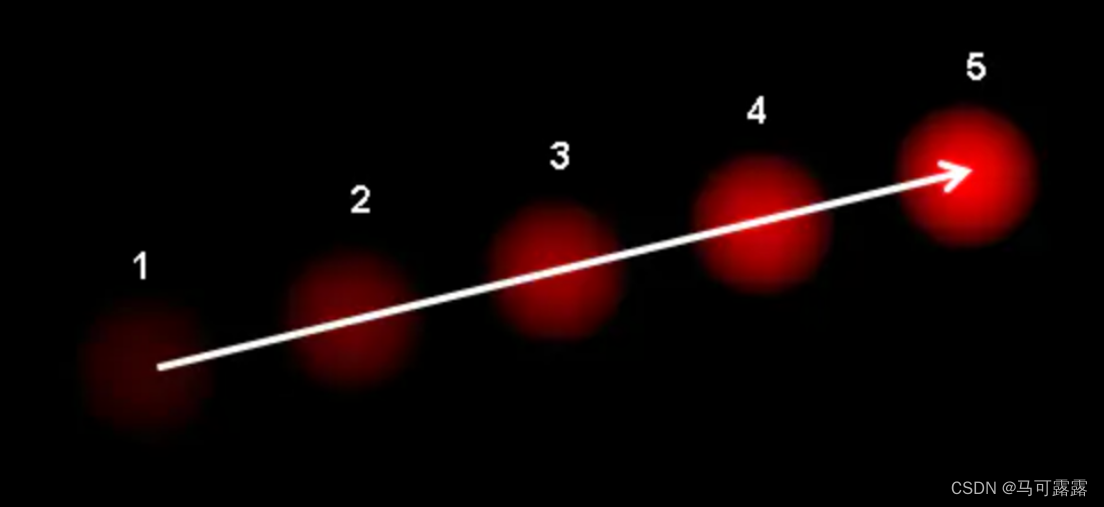
图中表示一个小球在连续5帧图像中的移动,箭头则表示小球的位移矢量。
简单来说,光流是空间运动物体在观测成像平面上的像素运动的“瞬时速度”,光流的研究是利用图像序列中的像素强度数据的时域变化和相关性来确定各自像素位置的“运动”,研究光流场的目的就是为了从图片序列中近似得到不能直接得到的现实中的运动场。
光流应用于诸多领域:
基于运动的三维重建
视频压缩
视频稳像
目标跟踪与行为识别
Lucas-Kanade 算法
光流生效的3个假设
1:亮度恒定:同一个像素点随着时间的变化,也就是说同一个像素点在位置变化前后的亮度值基本保持不变。
2:小范围运动:随着时间的变化,运动的变化,物体的运动不会产生剧烈的变化。这个情况下,灰度对位置的偏导数就可以近似
3:空间一致性:一个场景上,相临近的一块小区域内的点在运动变化后也是相临近的。
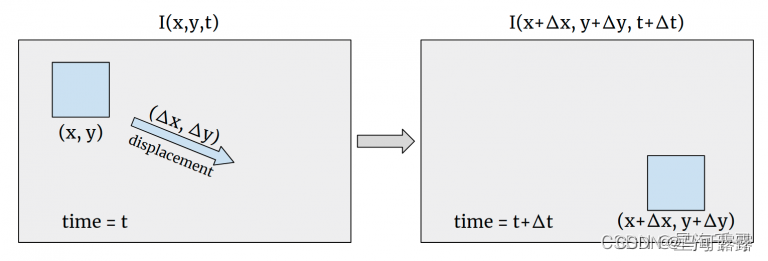
如上图展示的就是一张图像在时刻t到另一个时刻的某个像素的运动变化情况。

我们回想下之前的角点检测的
1、 在平面处,x的偏导的y的偏导是等于0的。
2、 在直线处,x的偏导的y的偏导有一个是等于0的。
3、 在角点处,x的偏导的y的偏导都变化很大,是有数值的。
这样看来,最有可能在角点处才能有方程的解。因此我们一般都是求角点的前后变化。
那么我们只需要比较前后帧的角点变化来做对比即可得到目标的运动方向。
Lucas-Kanade改进算法–图像金字塔
使用图像金字塔来改善LK光流
import cv2
import numpy as np
# cap = cv2.VideoCapture("images/kk 2022-01-23 18-21-21.mp4")
cap = cv2.VideoCapture(0)
# 定义角点检测的参数
feature_params = dict(
maxCorners=100, # 最多多少个角点
qualityLevel=0.3, # 品质因子,在角点检测中会使用到,品质因子越大,角点质量越高,那么过滤得到的角点就越少
minDistance=7 # 用于NMS,将最有可能的角点周围某个范围内的角点全部抑制
)
# 定义 lucas kande算法的参数
lk_params = dict(
winSize=(10, 10), # 这个就是周围点临近点区域的范围
maxLevel=2 # 最大的金字塔层数
)
# 拿到第一帧的图像
ret, prev_img = cap.read()
prev_img_gray = cv2.cvtColor(prev_img, cv2.COLOR_BGR2GRAY)
# 先进行角点检测,得到关键点
prev_points = cv2.goodFeaturesToTrack(prev_img_gray, mask=None, **feature_params)
# 制作一个临时的画布,到时候可以将新的一些画的先再mask上画出来,再追加到原始图像上
mask_img = np.zeros_like(prev_img)
while True:
ret, curr_img = cap.read()
if curr_img is None:
print("video is over...")
break
curr_img_gray = cv2.cvtColor(curr_img, cv2.COLOR_BGR2GRAY)
# 光流追踪下
curr_points, status, err = cv2.calcOpticalFlowPyrLK(prev_img_gray,
curr_img_gray,
prev_points,
None,
**lk_params)
# print(status.shape) # 取值都是1/0, 1表示是可以追踪到的,0表示失去了追踪的。
good_new = curr_points[status == 1]
good_old = prev_points[status == 1]
# 绘制图像
for i, (new, old) in enumerate(zip(good_new, good_old)):
a, b = new.ravel()
c, d = old.ravel()
mask_img = cv2.line(mask_img, pt1=(int(a), int(b)), pt2=(int(c), int(d)), color=(0, 0, 255), thickness=1)
mask_img = cv2.circle(mask_img, center=(int(a), int(b)), radius=2, color=(255, 0, 0), thickness=2)
# 将画布上的图像和原始图像叠加,并且展示
img = cv2.add(curr_img, mask_img)
cv2.imshow("desct", img)
if cv2.waitKey(60) & 0xFF == ord('q'):
print("Bye...")
break
# 更新下原始图像,以及重新得到新的点
prev_img_gray = curr_img_gray.copy()
prev_points = good_new.reshape(-1, 1, 2)
if len(prev_points) < 5:
# 当匹配的太少了,就重新获得当前图像的角点
prev_points = cv2.goodFeaturesToTrack(curr_img_gray, mask=None, **feature_params)
mask_img = np.zeros_like(prev_img) # 重新换个画布
cv2.destroyAllWindows()
cap.release()
DOF Dense Optical Flow in OpenCV
import numpy as np
import cv2
# cap = cv2.VideoCapture('./1.mp4')
cap = cv2.VideoCapture(0)
#获取第一帧
ret, frame1 = cap.read()
prvs = cv2.cvtColor(frame1, cv2.COLOR_BGR2GRAY)
hsv = np.zeros_like(frame1)
#遍历每一行的第1列
hsv[..., 1] = 255
#while True:
while(1):
ret, frame2 = cap.read()
next = cv2.cvtColor(frame2, cv2.COLOR_BGR2GRAY)
# 返回一个两通道的光流向量,实际上是每个点的像素位移值
flow = cv2.calcOpticalFlowFarneback(prvs, next, None, 0.5, 3, 15, 3, 5, 1.2, 0)
#print(flow.shape)
print(flow)
# 笛卡尔坐标转换为极坐标,获得极轴和极角
mag, ang = cv2.cartToPolar(flow[..., 0], flow[..., 1])
hsv[..., 0] = ang*180/np.pi/2
hsv[..., 2] = cv2.normalize(mag, None, 0, 255, cv2.NORM_MINMAX)
rgb = cv2.cvtColor(hsv, cv2.COLOR_HSV2BGR)
cv2.imshow('frame2', rgb)
k = cv2.waitKey(30) & 0xff
if k == 27:
break
elif k == ord('s'):
cv2.imwrite('opticalfb.png', frame2)
cv2.imwrite('opticalhsv.png', rgb)
prvs = next
cap.release()
cv2.destroyAllWindows()
CalcOpticalFlowFarneback()
是利用Gunnar Farneback的算法计算全局性的稠密光流算法(即图像上所有像素点的光流都计算出来),由于要计算图像上所有点的光流,故计算耗时,速度慢。它的核心思想主要源于”Two-Frame Motion Estimation Based on PolynomialExpansion”论文
CalcOpticalFlowFarneback()原理