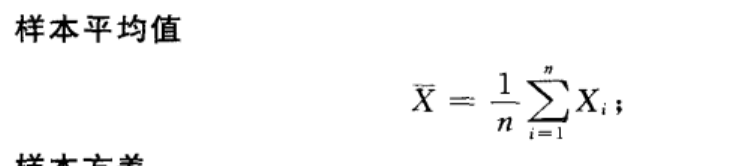定义：

在已知概率分布函数构造的情况下，概率分布的一些参数未知，如高斯分布的namda、方差，而利用采集到的参数来对未知参数进行估计就是参数估计。比较基础的有矩估计、最大似然估计。而不同的方法对未知参数估计可能有优劣之分，因此引出了如何评价参数估计方法的方法。

首先在参数估计中待估计参数也是一个随机变量，因此对此随机变量进行分析来判断其好坏

如何计算

待估计量的数学期望咋算？首先，前面的参数估计方法是采用采样得到的数据进行估计的，如x1,x2,x3...xn是采样得到的数据，而

g(x1,x2,x3,...,xn)是样本数据的函数，基本上参数估计方法都是类似函数g，而数据中xi每个都是一个随机变量，在概率论中，随机变量的函数也是一个随机变量，因此可以按照期望的规则来算，举个简单例子：

等式右边E(1\n*累加（xi))=1\n*累加（E(xi))由于E(xi)等于x的均值，因此最后说明样本均值的算法也是无偏估计。

具体计算的话就是利用那些公式，如E(X+Y)=E(X)+E(Y)等