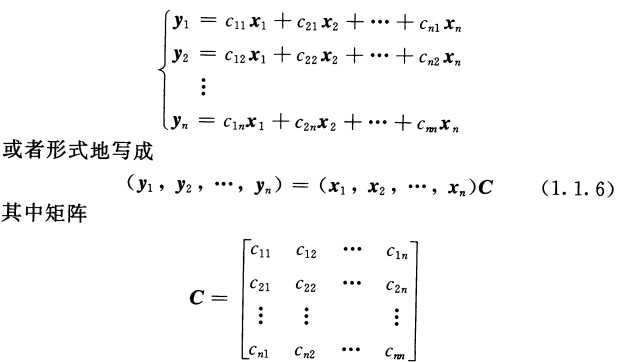PCA（Principal Component Analysis），即主成分分析，通常用于数据的降维处理。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维。
先从向量的内积(即点积)开始。首先，要解释的是，二维向量和这个二维向量在二维空间中对应的矩阵(线性变换)之间的关系。

• 1x2矩阵与二维向量之间的联系：二维空间中的二维向量所对应的1x2的矩阵，实际上就是改空间在这个二维向量方向上投影所做的线性变换的矩阵。

（其实如果注意到的话，实质上还与对偶性相关，即每一个坐标投影$(a,b)$都能找到唯一对应向量$(a,b)^T$）
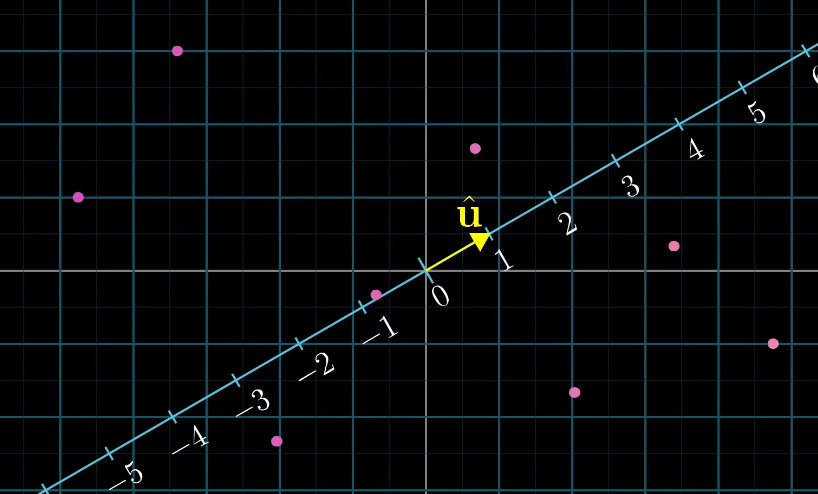
如下图所示，在二维空间中，我们有一个二维单位向量u，同时在该二维空间中，有多个二维向量(圆点表示)，则这些二维向量投影到u方向上的一维数轴上所对应的线性变换的矩阵，就是u在该二维空间所对应的坐标。

因此，向量的内积，实际上就是在一个向量方向上做线性变换。也就是高维空间的向量到低维子空间投影。
以三维为例，在三维空间中给定一个向量 U，以及由向量 V1，V2 构成的一个二维平面，向量 P 为 u 到这个平面的投影，它是 V1，V2 的线性组合：$P=c_{1}V_{1} +c_{2}V_{2}$ .
利用性质$(U-P)⊥(V1，V2)$,
也就是求：
$(U-P)^{T}V=\bar{0}$ ，
从而可以求得：
$C=(V^{T} V)^{-1} V^{T} U$

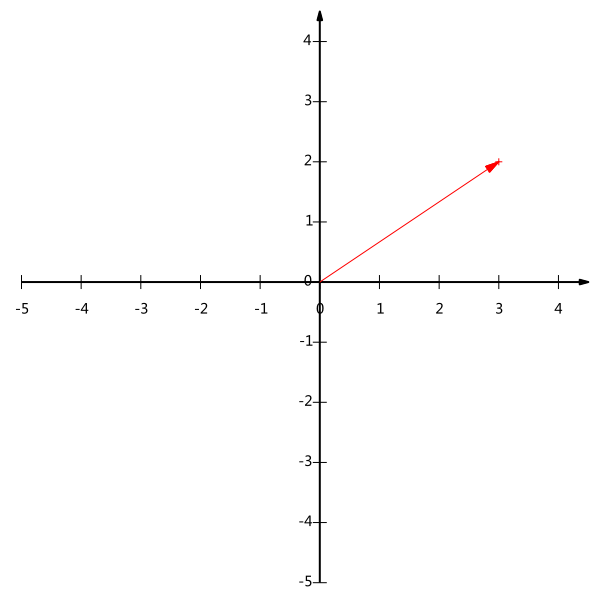
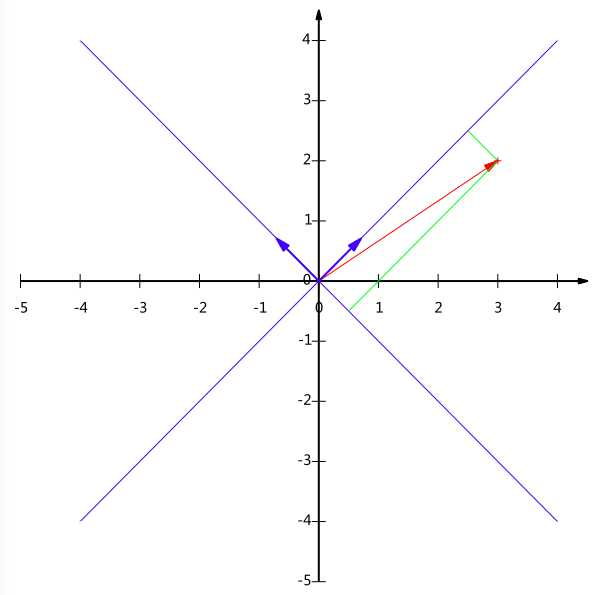
下面我们继续在二维空间内讨论向量。上文说过，一个二维向量可以对应二维笛卡尔直角坐标系中从原点出发的一个有向线段。例如下面这个向量：

在代数表示方面，我们经常用线段终点的点坐标表示向量，例如上面的向量可以表示为(3,2)，这是我们再熟悉不过的向量表示。

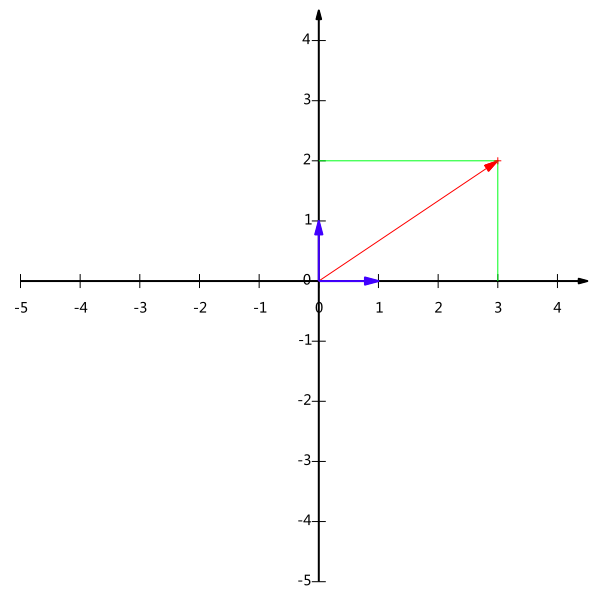
不过我们常常忽略，只有一个(3,2)本身是不能够精确表示一个向量的。我们仔细看一下，这里的3实际表示的是向量在x轴上的投影值是3，在y轴上的投影值是2。也就是说我们其实隐式引入了一个定义：以x轴和y轴上正方向长度为1的向量为标准。那么一个向量(3,2)实际是说在x轴投影为3而y轴的投影为2。注意投影是一个矢量，所以可以为负。
更正式的说，向量(x,y)实际上表示线性组合：
$x(1,0)^T+y(1,0)^T$

其中，$x(1,0)^T、y(1,0)^T$ 为二维空间中的一对基。

所以，要准确描述向量，首先要确定一组基，然后给出在基所在的各个直线上的投影值，就可以了。

我们之所以默认选择(1,0)和(0,1)为基，当然是比较方便，只不过我们经常省略第一步，而默认以(1,0)和(0,1)为基。因为它们分别是x和y轴正方向上的单位向量，因此就使得二维平面上点坐标和向量一一对应，非常方便。但实际上任何两个线性无关的二维向量都可以成为一组基，所谓线性无关在二维平面内可以直观认为是两个不在一条直线上的向量。

例如，(1,1)和(-1,1)也可以成为一组基。一般来说，我们希望基的模是1，因为从内积的意义可以看到，如果基的模是1，那么就可以方便的用向量点乘基而直接获得其在新基上的坐标了！实际上，对应任何一个向量我们总可以找到其同方向上模为1的向量，只要让两个分量分别除以模就好了。例如，上面的基可以变为

$(\frac{1}{\sqrt2},\frac{1}{\sqrt2}),(-\frac{1}{\sqrt2},\frac{1}{\sqrt2})$

现在我们想获得（3,2）在新基上的坐标，即在两个方向上的投影矢量值。
根据程云鹏的矩阵论11页上的定义：设x1，x2，…，xn是Vn的旧基，y1，y2，…，yn为其新基，则由基的定义可以写为（y1，y2，…，yn）=（x1，x2，…，xn）C（此处y和x均为列向量）

其中C称之为过渡矩阵

所以我们有$Y=X*C$

其中Y为$\left( \begin{array}{ccc}\frac{1}{\sqrt{2} } &-\frac{1}{\sqrt{2} } \\\frac{1}{\sqrt{2} }&\frac{1}{\sqrt{2} }\end{array}\right) ,X为\left( \begin{array}{ccc}1&0 \\0&1 \end{array}\right) ,可得C为\left( \begin{array}{ccc}\frac{1}{\sqrt{2} } &-\frac{1}{\sqrt{2} } \\\frac{1}{\sqrt{2} }&\frac{1}{\sqrt{2} }\end{array}\right)$

那么根据程云鹏的矩阵论书中，坐标在新基中的表示为$C^{-1}*\left( \begin{array}{ccc}3 \\2 \end{array}\right) =\left( \begin{array}{ccc}\frac{5}{\sqrt{2} } \\-\frac{1}{\sqrt{2} } \end{array}\right)$

我们可以看到C明显为正交矩阵，正交矩阵的性质为：正交矩阵的逆等于其转置

正交矩阵的逆等于其转置,所以本来C的第一列为基，求逆矩阵之后变成C的第一行为基。
所以推导出下面这个式子。
一般的，如果我们有M个N维向量，想将其变换为由R个N维向量表示的新空间中，那么首先将R个基按行组成矩阵A，然后将向量按列组成矩阵B，那么两矩阵的乘积AB就是变换结果，其中AB的第m列为A中第m列变换后的结果。

数学表示为：

特别要注意的是，这里R可以小于N，而R决定了变换后数据的维数。也就是说，我们可以将一N维数据变换到更低维度的空间中去，变换后的维度取决于基的数量。因此这种矩阵相乘的表示也可以表示降维变换。

最后，上述分析同时给矩阵相乘找到了一种物理解释：两个矩阵相乘的意义是将右边矩阵中的每一列列向量变换到左边矩阵中每一行行向量为基所表示的空间中去。更抽象的说，一个矩阵可以表示一种线性变换。

了解了内积的定义后，我们就可以对PCA有进一步的了解。

明天更？