【机器学习基础】第三课：模型性能度量

【机器学习基础】系列博客为参考周志华老师的《机器学习》一书，自己所做的读书笔记。

1.均方误差

使用不同的性能度量往往会导致不同的评判结果。

例如， $f (x)$ 为预测结果， $y$ 为真实标记。

回归问题中，最常用的性能度量为“均方误差”：

$E(f;D)=\frac{1}{m}\sum_{i=1}^m(f(x_i)-y_i)^2$

更一般的，对于数据分布 $D$ 和概率密度函数 $p(\cdot)$ ，均方误差可描述为：

$E(f;D)=\int_{x\sim D}(f(x)-y)^2 p(x)dx$

2.错误率与精度

更一般的，对于数据分布 $D$ 和概率密度函数 $p(\cdot)$

错误率： $E(f;D)=\int_{x\sim D}\Pi (f(x)\neq y)p(x)dx$
精度： $acc(f;D)=\int_{x\sim D}\Pi (f(x)=y)p(x)dx=1-E(f;D)$

$\Pi (\cdot)$ ：指示函数，在 $\cdot$ 为真和假时分别取值为1，0。

3.查准率、查全率与 $F_1$

查准率，亦称“准确率”：precision
查全率，亦称“召回率”：recall

混淆矩阵：

查准率： $P=\frac{TP}{TP+FP}$

查全率： $R=\frac{TP}{TP+FN}$

一般情况下，查全率和查准率是一对矛盾的度量，一个高一个底。
通常只有在一些简单任务中，才可能使查全率和查准率都很高。

3.1.“P-R曲线”

根据学习器的预测结果对样例进行排序，排在前面的是学习器认为“最可能”是正例的样本，排在最后的则是学习器认为“最不可能”是正例的样本，按此顺序逐个把样本作为正例进行预测，则每次可以计算出当前的查全率、查准率。

举例解释一下：例如一个二分类问题，按照预测为正例的概率从大到小进行排序：

绘制“P-R”曲线的步骤：

预测为正例的概率从大到小排列。
构建二维直角坐标系，横轴为查全率，纵轴为查准率。
阈值在(0)处时，有 $TP = FP = 0$ ，即分类器预测全为负例，此时 $P = R = 0$ ，得到“P-R曲线”的第一个点(0,0)。
阈值在(1)处时，大于该阈值的样本被预测为正例，小于该阈值的样本被预测为负例，结合样本的真实标记构建混淆矩阵，从而计算查准率和查全率，得到第二个点的坐标。
其余点以此类推。
阈值在(n)时，得到最后一个点，分类器预测全为正例， $FN = TN = 0$ ，此时查全率为1，查准率实际为数据集中正例所占的比例（如果数据集为平衡数据， $P\approx 0.5$ ，此时最后一个点的坐标为(1,0.5)）。

因此，根据上述步骤，将得到的多个点连接起来，得到“P-R曲线”（或者叫“P-R图”）。

⚠️为绘图方便和美观，“P-R曲线”通常绘制成单调平滑曲线，但现实任务中的“P-R曲线”常是非单调、不平滑的，在很多局部有上下波动。

3.1.1.通过“P-R曲线”评价模型性能的优劣

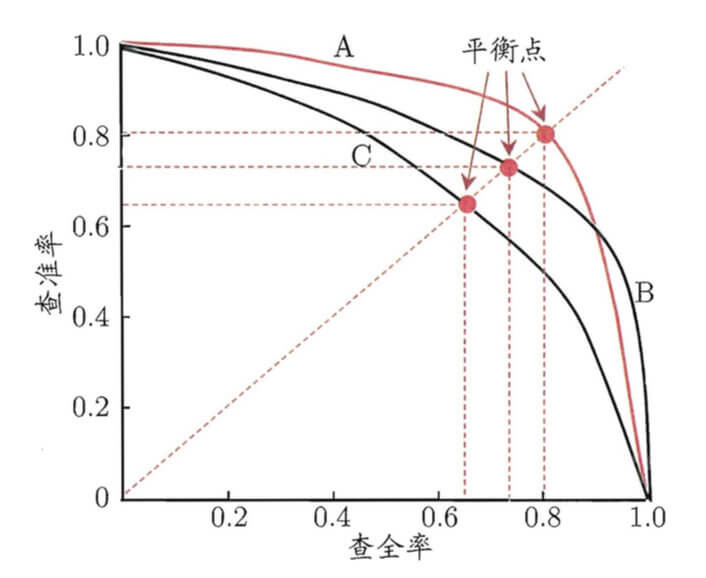
“P-R曲线”与平衡点示意图：

若一个学习器的“P-R曲线”被另一个学习器的曲线完全“包住”，则可断言后者的性能优于前者，如上图中学习器A的性能优于学习器C。

如果两个学习器的“P-R曲线”发生了交叉，例如A和B，则难以一般性地断言两者孰优孰劣，只能在具体的查准率或查全率下进行比较。

常用的比较方法有以下三种：

曲线下面积。
平衡点（Break-Event Point，简称BEP），它是“查准率=查全率”时的取值。如C的 $BEP = 0.64$ ，A优于B（因为A的BEP>B的BEP）等。
BEP还是过于简单，引入F值。

3.2.F值

$F_\beta=\frac{(1+\beta^2)\times P\times R}{(\beta^2 \times P)+R}$

其中 $\beta (\beta >0)$ 度量了查全率对查准率的相对重要性。

$\beta =1$ 时，即 $F_1$ ，查全率和查准率的重要性相当。
$\beta >1$ 时，查全率有更大影响。
$\beta <1$ 时，查准率有更大影响。

$F_1$ 是基于查准率和查全率的调和平均，定义为： $\frac{1}{F_1}=\frac{1}{2}(\frac{1}{P}+\frac{1}{R})$

$F_\beta$ 则是加权调和平均， $\frac{1}{F_\beta}=\frac{1}{1+\beta^2}(\frac{1}{P}+\frac{\beta^2}{R})$

tips：与算数平均 $(\frac{P+R}{2})$ 和几何平均 $(\sqrt{P\times R})$ 相比，调和平均更重视较小值（更适合评价不平衡数据的分类问题）。

相关知识补充：

常见的三种平均数：算数平均数、几何平均数、调和平均数。

这里主要介绍一下调和平均数。

调和平均数（harmonic mean）又称倒数平均数，是各种统计变量倒数的算数平均数的倒数。主要分为两种类型：简单调和平均数和加权调和平均数。

简单调和平均数：

$H_n=\frac{1}{\frac{1}{n}\sum_{i=1}^n\frac{1}{x_i}}=\frac{n}{\sum_{i=1}^n\frac{1}{x_i}}$

加权调和平均数：

$\begin{align} H_n & = \frac{1}{\frac{1}{m_1+m_2+\cdots +m_n}(\frac{1}{x_1}m_1+\frac{1}{x_2}m_2+\cdots +\frac{1}{x_n}m_n)} \\&= \frac{\sum_{i=1}^n m_i}{\sum_{i=1}^n \frac{m_i}{x_i}} \end{align}$

3.2.1.宏 $F_1$ 和微 $F_1$

如果：

进行多次训练/测试，每次得到一个混淆矩阵；
在多个数据集上进行训练/测试，希望估计算法的“全局”性能；
执行多分类任务，每两两类别的组合都对应一个混淆矩阵；
其他类似情况…

解决办法：引入宏 $F_1$ 和微 $F_1$ 。

3.2.1.1.宏 $F_1$

先在各混淆矩阵上分别计算查全率和查准率，记为( $P_1,R_1$ )，( $P_2,R_2$ )，…，( $P_n,R_n$ )，再计算平均值。

宏查准率： $macro-P=\frac{1}{n}\sum_{i=1}^n P_i$

宏查全率： $macro-R=\frac{1}{n}\sum_{i=1}^n R_i$

宏 $F_1$ ： $macro-F_1=\frac{2\times macro-P\times macro-R}{macro-P+macro-R}$

3.2.1.2.微 $F_1$

先将各混淆矩阵的对应元素进行平均，得到 $TP, FP, TN, FN$ 的平均值，分别记为 $\overline{TP},\overline{FP},\overline{TN},\overline{FN}$ ，再基于这些平均值计算。

微查准率： $micro-P=\frac{\overline{TP}}{\overline{TP}+\overline{FP}}$

微查全率： $micro-R=\frac{\overline{TP}}{\overline{TP}+\overline{FN}}$

微 $F_1$ ： $micro-F_1=\frac{2\times micro-P \times micro-R}{micro-P+micro-R}$

4.ROC与AUC

很多学习器是为测试样本产生一个实值或者概率预测，然后将这个预测值与一个分类阈值(threshold)进行比较，若大于阈值则分为正类，否则为反类。

依旧使用前文3.1部分的概率输出结果作为一个例子：

若更重视“查准率”，则可选择排序靠前的位置进行截断。
若更重视“查全率”，则可选择排序靠后的位置进行截断。

ROC：“受试者工作特征”（Receiver Operating Characteristic）曲线。

在ROC中：

横轴：“假阳性率”（False Positive Rate,FPR）。

$FPR=\frac{FP}{TN+FP}$

纵轴：“真阳性率”（True Positive Rate,TPR）。

$TPR=\frac{TP}{TP+FN}$

绘制ROC步骤：

当阈值设在(0)处时，分类器将所有样本预测为负例，此时 $FPR = TPR = 0$ ，得到第一个点：(0,0)。
其余点以此类推。
当阈值设在(n)处时，分类器将所有样本预测为正例，即 $TN = FN = 0$ ，有 $FPR = TPR = 1$ ，得到最后一个点：(1,1)。

根据上述步骤可得到ROC，见下图：

点(0,1)处完美分类。

现实任务中通常是利用有限个测试样例来绘制ROC图，此时仅能获得有限个(FPR,TPR)坐标对，无法产生图(a)中光滑的ROC曲线，只能绘制出如图(b)中所示的近似ROC曲线（类比“P-R曲线”的绘制）。

进行学习器比较时，使用AUC（Area Under ROC Curve）值，即ROC曲线下面积。

5.代价敏感错误率与代价曲线

不同类型的错误所造成的后果不同。如错误地把患者诊断为健康人与错误地把健康人诊断为患者，造成的后果的代价是不同的。

为权衡不同类型错误所造成的损失，可为错误赋予“非均等代价”。

以二分类任务为例，可根据任务的领域知识设定一个“代价矩阵”，其中 $cost_{ij}$ 表示将第i类样本预测为第j类样本的代价。二分类代价矩阵见下图：

一般来说， $cost_{ii}=0$ 。
若将第0类判别为第1类所造成的损失更大，则 $cost_{01}>cost_{10}$ 。
损失程度相差越大， $cost_{01}$ 与 $cost_{10}$ 值的差别越大。
一般情况下，重要的是代价比值而非绝对值，例如 $cost_{01}:cost_{10}=5:1$ 与 $50 : 10$ 所起效果相当。

前面介绍的性能度量，它们大都隐式地假设了均等代价。在非均等代价下，目标应该是最小化“总体代价”。

将第0类作为正类，第1类作为反类，令 $D^+$ 与 $D^-$ 分别代表样例集D的正例子集和反例子集，则“代价敏感错误率”为：

$E(f;D;cost)=\frac{1}{m}(\sum_{x_i\in D^+}\prod (f(x_i)\neq y_i)\times cost_{01}+\sum_{x_i\in D^-}\prod (f(x_i)\neq y_i)\times cost_{10})$

（结合上文中的错误率公式进行理解。类似的，可给出基于分布定义的代价敏感错误率。若令 $cost_{ij}$ 中的i,j取值不限于0，1，则可定义出多分类任务的代价敏感性能度量。）

在非均等代价下，ROC曲线不能直接反映出学习器的期望总体代价，而“代价曲线”则可达到该目的。

代价曲线的横轴：取值为 $[0, 1]$ 的正例概率代价：

$P(+)cost=\frac{p\times cost_{01}}{p\times cost_{01}+(1-p)\times cost_{10}}\tag{1}$

其中 $p$ 是样例为正例的概率。

代价曲线的纵轴：取值为 $[0, 1]$ 的归一化代价：

$cost_{norm}=\frac{FNR\times p\times cost_{01}+FPR\times (1-p)\times cost_{10}}{p\times cost_{01}+(1-p)\times cost_{10}}\tag{2}$

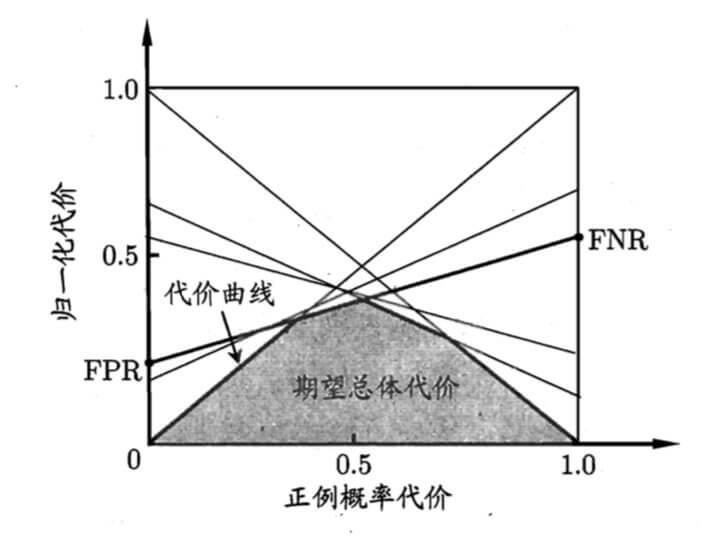
设ROC曲线上点的坐标为 $(FPR, TPR)$ ，可对应地，在代价平面上绘制一条从 $(0, FPR)$ 到 $(1 ， FNR)$ 的线段，线段下的面积即表示了该条件下的期望总体代价；如此将ROC曲线上的每个点转化为代价平面上的一条线段，然后取所有线段的下界，围成的面积即为在所有条件下学习器的期望总体代价。见下图：

代价曲线上的每一点对应的都是最小的归一化代价（无论哪个阈值）。图中每一条线都对应ROC中的一个点，对应一个相应的阈值 $\eta$ 。相比ROC，代价曲线多考虑了p，即正例先验概率。

5.1.关于式（2）的推导

先只看单个分类器的期望代价，假设我们的分类器是： $\underset{decide\ H_1}{\overset{decide\ H_0}{\gtrless}}\eta$

则该分类器的期望代价就是：

$E[Cost]=\sum_{i=0}^1 \sum_{j=0}^1 C_{ij}Pr[decide\ H_i\mid H_j]Pr[H_j]$

其中：

$C_{ij}$ 来自于代价矩阵，即 $cost_{ij}$
$Pr[decide\ H_i\mid H_j]$ 为条件概率
- $Pr[decide\ H_0\mid H_1]=FPR$
- $Pr[decide\ H_1\mid H_1]=TNR$
- $Pr[decide\ H_1\mid H_0]=FNR$
- $Pr[decide\ H_0\mid H_0]=TPR$
$Pr[H_j]$ 是先验概率，即 $Pr[H_0]=p,Pr[H_1]=1-p$

又因为有 $cost_{00}=cost_{11}=0$ ，所以有：

$E[Cost]=FNR\times p\times cost_{01}+FPR\times (1-p)\times cost_{10}$

即为式（2）中分子，即未归一化的期望代价。

若要对其进行归一化处理（压缩至[0，1]区间），可除以最大代价期望，即全部分错的情况， $TN = TP = 0$ ，最大代价期望为： $p\times cost_{01}+(1-p)\times cost_{10}$ 。据此便可得到式（2）。

5.2.关于式（1）的推导

未归一化的 $E [C os t]$ 与p呈线性相关，描述某一阈值下，p与 $E [C os t]$ 的关系： $\int_0^1E[Cost]dp$ 可以表示某一阈值下的总代价期望。

归一化的 $cost_{norm}$ 不与p呈线性相关，那么 $(0, FPR)$ 到 $(1, FNR)$ 之间的连线可能就不是线段，可能会是非常复杂的曲线（并且不一定在二维空间内），取所有曲线的下界，并求其围成的面积是非常困难的。

“规范化”和“归一化”
“规范化”是将不同变化范围内的值映射到相同的固定范围中，常见的是[0,1]，此时亦称“归一化”。

那么在归一化 $cost_{norm}$ 后，如何保证 $(0, FPR)$ 到 $(1, FNR)$ 之间的连线依旧是线段呢？

答：假设线段的两点分别是 $A : (0, FPR)$ 和 $B : (1, FNR)$ ，如果想表示AB连线上所有点的集合就用 $\lambda A+(1-\lambda)B,\lambda \in [0,1]$ ，通过变化 $\lambda$ ，我们可以得到线段AB。则线段AB上任意一点的纵坐标为： $\lambda FPR+(1-\lambda)FNR=cost_{norm}$ 。因此可以得到 $1-\lambda =\frac{p\times cost_{01}}{p\times cost_{01}+(1-p)\times cost_{10}}$ ， $\lambda=\frac{(1-p)\times cost_{10}}{p\times cost_{01}+(1-p)\times cost_{10}}$ 。又线段AB上任意一点的横坐标为： $\lambda \times 0+(1-\lambda)\times 1=\frac{p\times cost_{01}}{p\times cost_{01}+(1-p)\times cost_{10}}=P(+)cost$ 。