【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
1.比较检验
先使用某种实验评估方法测得学习器的某个性能度量结果,然后对结果进行比较,不能单纯地直接取得性能度量的值然后“比”大小,需要有统计学意义。
在现实任务中我们并不知道学习器的泛化错误率,只能获知其测试错误率。因此本文以测试错误率作为性能度量。
2.假设检验
关于假设检验(以单样本t检验为例,样本均数为 μ 0 \mu_0 μ0,总体均数为 μ \mu μ):
- μ = μ 0 \mu=\mu_0 μ=μ0:即检验假设,常称无效假设或零(原)假设,用 H 0 H_0 H0表示。
- μ ≠ μ 0 \mu\neq \mu_0 μ=μ0(或 μ > μ 0 \mu>\mu_0 μ>μ0, μ < μ 0 \mu<\mu_0 μ<μ0等):即备择假设,常称对立假设,用 H 1 H_1 H1或 H A H_A HA表示。
除此之外,还需要注意:
- 检验假设针对的是总体,而不是样本。
- H 0 H_0 H0为无效假设,其假定通常是:某两个(或多个)总体参数相等,或两个总体参数之差为0,或某资料服从某一特定分布(如正态分布,泊松分布)或某些情况无效等。
- 不拒绝 H 0 H_0 H0不等于接受 H 0 H_0 H0。下结论时,对 H 0 H_0 H0只能说拒绝 H 0 H_0 H0或不拒绝 H 0 H_0 H0,而对 H 1 H_1 H1只能说接受 H 1 H_1 H1,除此之外的其他说法均不妥当。
假设检验常用的有两大类:
- 参数检验(parametric test)
- 非参数检验(nonparametric test)
2.1.参数检验
如果总体分布为已知的数学形式,对其总体参数做假设检验称为参数检验。
例如:t检验和F检验。
⚠️使用t检验和F检验的两个前提条件:1)正态分布总体;2)方差齐性。
2.1.1.t检验,F检验前提条件检验
👉正态性检验:
- 图示法
- 概率图(probability-probability plot,P-P plot)
- 分位数图(quantile-quantile plot,Q-Q plot)
- 计算法
- 对偏度(skewness)和峰度(kurtosis)各用一个指标来评定,其中以矩法(method of moment),又称动差法,效率最高。
- 仅用一个指标来综合评定,其中以 W W W检验法和 W ′ W' W′检验法效率最高,适用于样本含量少于100的资料; D D D检验法效率也高,适用于样本含量 n n n为10~2000的资料。
👉方差齐性检验:
- 两样本方差比较:F检验、Levene检验。
- 多样本方差比较:Bartlett检验、Levene检验、F检验。
2.2.非参数检验
但是:
- 当总体分布不能由已知的数学形式表达,没有总体参数时,不能使用参数检验。
- 两个或多个正态总体方差不等时,不能对其总体均数进行t检验或F检验的参数检验。
对于这种情况,有两种解决办法:一是可尝试变量变换使其满足参数检验条件,但不一定能成功;二是使用非参数检验。对于等级资料,常使用非参数检验。
非参数检验对总体分布不作严格假定,又称任意分布检验。例如:秩检验和卡方检验。
3.参数检验之t检验
先补充两方面的知识:
👉标准误:
通常,将样本统计量的标准差称为标准误。
样本均数的标准差称为均数的标准误,即
σ x ˉ = σ n \sigma_{\bar x}=\frac{\sigma}{\sqrt{n}} σxˉ=nσ
其中, σ x ˉ \sigma_{\bar x} σxˉ为均数标准误, σ \sigma σ为总体标准差, n n n为样本量。
总体标准差和样本标准差:
总体标准差: σ = ∑ ( x − μ ) 2 N \sigma=\sqrt{\frac{\sum (x-\mu)^2}{N}} σ=N∑(x−μ)2
样本标准差: S = ∑ ( x − x ˉ ) 2 n − 1 S=\sqrt{\frac{\sum (x-\bar x)^2}{n-1}} S=n−1∑(x−xˉ)2
数理统计证明:若用样本个数n代替N,计算出的样本方差对 σ 2 \sigma ^2 σ2的估计偏小,需将n用n-1代替。
在实际工作中,由于总体标准差 σ \sigma σ常常未知,而用样本标准差S来估计,因此均数标准误的估计值为:
S x ˉ = S n S_{\bar x}=\frac{S}{\sqrt{n}} Sxˉ=nS
👉t分布:
若某一随机变量 X X X服从总体均数为 μ \mu μ,总体标准差为 σ \sigma σ的正态分布 N ( μ , σ 2 ) N(\mu,\sigma ^2) N(μ,σ2),则通过 u u u变换( X − μ σ \frac{X-\mu}{\sigma} σX−μ,也称 Z Z Z变换)可将一般正态分布转化为标准正态分布 N ( 0 , 1 2 ) N(0,1^2) N(0,12),即 u u u分布(也称 Z Z Z分布)。
同理,若样本含量为 n n n的样本均数 X ˉ \bar X Xˉ服从总体均数为 μ \mu μ,总体标准差为 σ X ˉ \sigma_{\bar X} σXˉ的正态分布 N ( μ , σ X ˉ 2 ) N(\mu ,\sigma_{\bar X}^2) N(μ,σXˉ2),则通过同样方式的 u u u变换 ( X ˉ − μ σ X ˉ ) (\frac{\bar X-\mu}{\sigma_{\bar X}}) (σXˉXˉ−μ)也可将其转换为标准正态分布 N ( 0 , 1 2 ) N(0,1^2) N(0,12),即 u u u分布。
但在实际工作中, σ X ˉ \sigma_{\bar X} σXˉ常常未知,用 S X ˉ S_{\bar X} SXˉ代替,则 X ˉ − μ S X ˉ \frac{\bar X-\mu}{S_{\bar X}} SXˉXˉ−μ不再服从标准正态分布,而服从t分布。即
t = X ˉ − μ S X ˉ = X ˉ − μ S / n , v = n − 1 t=\frac{\bar X-\mu}{S_{\bar X}}=\frac{\bar X-\mu}{S/\sqrt n},v=n-1 t=SXˉXˉ−μ=S/nXˉ−μ,v=n−1
自由度:
上式中 v v v为自由度。在数学上指能够自由取值的变量个数。
如 X + Y + Z = 18 X+Y+Z=18 X+Y+Z=18,有三个变量,但能够自由取值的只有两个,故自由度 v = 2 v=2 v=2,在统计学中自由度通常按下式计算: v = n − m v=n-m v=n−m。其中, n n n为计算某一统计量时用到的数据个数; m m m为计算该统计量时用到其他独立统计量的个数。
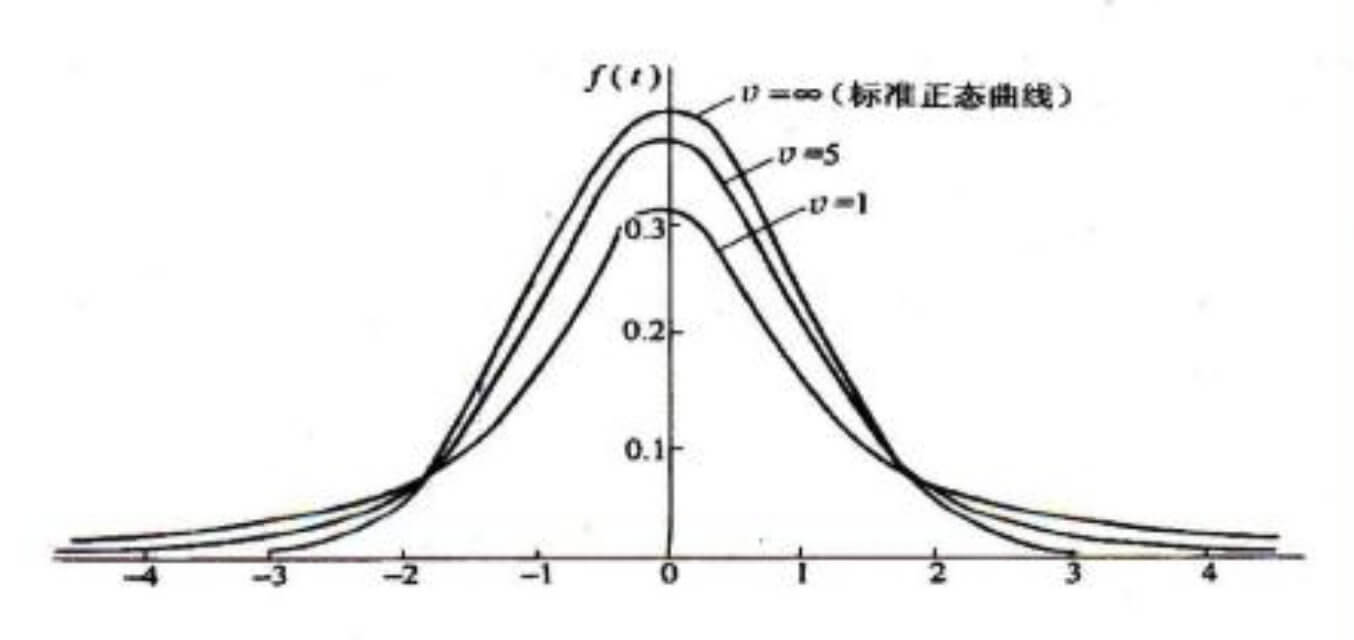
t分布图形与特征(概率密度函数曲线):
t分布图有如下特征:
- 单峰分布,以0为中心,左右对称;
- t分布的曲线形态取决于自由度 v v v的大小,自由度 v v v越小,则t值越分散,曲线的峰部越矮而尾部翘得越高;
- 当 v v v逼近 ∞ \infty ∞, S X ˉ S_{\bar X} SXˉ逼近 σ x ˉ \sigma_{\bar x} σxˉ,t分布逼近标准正态分布。当自由度趋于 ∞ \infty ∞时,t分布就是标准正态分布,故标准正态分布就是t分布的特例。
3.1.单样本t检验
单样本t检验即已知样本均数 X ˉ \bar X Xˉ(代表未知总体均数 μ \mu μ)与已知总体均数 μ 0 \mu_0 μ0(一般为理论值、标准值或经过大量观察所得的稳定值等)的比较。公式见下:
t = X ˉ − μ S X ˉ = X ˉ − μ S / n = X ˉ − μ 0 S / n , v = n − 1 t=\frac{\bar X-\mu}{S_{\bar X}}=\frac{\bar X-\mu}{S/\sqrt n}=\frac{\bar X-\mu_0}{S/\sqrt n},v=n-1 t=SXˉXˉ−μ=S/nXˉ−μ=S/nXˉ−μ0,v=n−1
3.2.配对样本t检验
公式见下(若两种处理效应相同):
t = d ˉ − μ d S d ˉ = d ˉ − 0 S d / n = d ˉ S d / n , v = n − 1 t=\frac{\bar d-\mu_d}{S_{\bar d}}=\frac{\bar d-0}{S_d/\sqrt n}=\frac{\bar d}{S_d/\sqrt n},v=n-1 t=Sdˉdˉ−μd=Sd/ndˉ−0=Sd/ndˉ,v=n−1
其中, d d d为每对数据的差值, d ˉ \bar d dˉ为差值的样本均数, S d S_d Sd为差值的标准差, S d ˉ S_{\bar d} Sdˉ差值样本均数的标准误, n n n为对子数。
3.2.1.配对样本t检验的应用场景举例
对于两个学习器 A A A和 B B B,若使用 k k k折交叉验证法得到的测试错误率分别为 ϵ 1 A , ϵ 2 A , . . . , ϵ k A \epsilon_1^A,\epsilon_2^A,...,\epsilon_k^A ϵ1A,ϵ2A,...,ϵkA和 ϵ 1 B , ϵ 2 B , . . . , ϵ k B \epsilon_1^B,\epsilon_2^B,...,\epsilon_k^B ϵ1B,ϵ2B,...,ϵkB,其中 ϵ i A \epsilon_i^A ϵiA和 ϵ i B \epsilon_i^B ϵiB是在相同的第 i i i折训练/测试集上得到的结果。此时便可采用配对样本t检验对学习器A和B进行比较。
⚠️但是欲进行有效的假设检验,一个重要前提是测试错误率均为泛化错误率的独立采样。⚠️
在使用交叉验证等实验估计方法时,不同轮次的训练集会有一定程度的重叠,这就使得测试错误率实际上并不独立,会导致过高估计假设成立的概率。
为缓解这一问题,可采用“ 5 × 2 5\times 2 5×2交叉验证”法,即做5次2折交叉验证。
例如第
i
i
i次2折交叉验证:
每一轮次的训练集没有重叠,互相独立。
3.3.两样本t检验
当两样本含量较小[如 n 1 ⩽ 60 n_1\leqslant60 n1⩽60或(和) n 2 ⩽ 60 n_2\leqslant60 n2⩽60],且均来自正态总体时,要根据两总体方差是否相等而采用不同检验方法。
3.3.1.总体方差相等的t检验
当两总体方差相等,即 σ 1 2 = σ 2 2 \sigma^2_1=\sigma^2_2 σ12=σ22时,两样本t检验的检验统计量在 H 0 : μ = μ 1 − μ 2 = μ 0 = 0 H_0:\mu=\mu_1-\mu_2=\mu_0=0 H0:μ=μ1−μ2=μ0=0条件下构造:
t = X 1 ˉ − X 2 ˉ ( n 1 − 1 ) S 1 2 + ( n 2 − 1 ) S 2 2 n 1 + n 2 − 2 ( 1 n 1 + 1 n 2 ) , v = n 1 + n 2 − 2 t=\frac{\bar{X_1}-\bar{X_2}}{\sqrt{\frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2}(\frac{1}{n_1}+\frac{1}{n_2})}},v=n_1+n_2-2 t=n1+n2−2(n1−1)S12+(n2−1)S22(n11+n21)X1ˉ−X2ˉ,v=n1+n2−2
若两总体方差不等,即 σ 1 2 ≠ σ 2 2 \sigma_1^2\neq\sigma_2^2 σ12=σ22时,可采用数据变换(如两样本几何均数的t检验,就是将原始数据取对数后进行t检验)或进行近似t检验---- t ′ t' t′检验或秩转换的非参数检验。
近似t检验有三种方法可供选择:
- Cochran&Cox法
- Satterthwaite法
- Welch法
其中,前两种方法比较常用。此处不再详述这三种方法。
4.参数检验之F检验
方差分析(analysis of variance,ANOVA)又称F检验,用于多个样本均数的比较。
本部分只是简单介绍各个方法的应用区别,不深究公式和计算。
4.1.完全随机设计资料的方差分析
完全随机设计(completely random design)是采用完全随机化的分组方法,将全部实验对象分配到 g g g个处理组(水平组),各组分别接受不同的处理,实验结束后比较各组均数之间的差别有无统计学意义,推论处理因素的效应。
通过一个例题来了解完全随机设计:
某医生为了研究一种降血脂新药的临床疗效,按照统一纳入标准选择120名高血脂患者,采用完全随机设计方法将患者等分为4组,进行双盲实验。6周后测得低密度脂蛋白作为试验结果(见下表)。问4个处理组患者的低密度脂蛋白含量总体均数有无差别?
| 分组 | 测量值 |
|---|---|
| 安慰剂组 | 3.53 4.59 4.34 2.66 …(剩余略) |
| 降血脂新药2.4g组 | 2.42 3.36 4.32 2.34 …(剩余略) |
| 降血脂新药4.8g组 | 2.86 2.28 2.39 2.28 …(剩余略) |
| 降血脂新药7.2g组 | 0.89 1.06 1.08 1.27 …(剩余略) |
其中, g = 4 g=4 g=4, H 0 : μ 1 = μ 2 = μ 3 = μ 4 H_0:\mu_1=\mu_2=\mu_3=\mu_4 H0:μ1=μ2=μ3=μ4,即4个试验组的总体均数相等。
4.2.随机区组设计资料的方差分析
随机区组设计(randomized block design)又称为配伍组设计,是配对设计的扩展。具体做法是:先按影响实验结果的非处理因素(如性别、体重、年龄、职业、病情、病程等)将实验对象配成区组(block),再分别将各区组内的实验对象随机分配到各处理组或对照组。
通过一个例子来理解:
某研究者采用随机区组设计进行实验,比较三种抗癌药物对小白鼠肉瘤的抑瘤效果,先将15只染有肉瘤小白鼠按体重大小配成5个区组,每个区组内3只小白鼠随机接受三种抗癌药物,以肉瘤的重量为指标,实验结果见下表。问三种不同药物的抑瘤效果有无差别?
| 区组 | A药 | B药 | C药 |
|---|---|---|---|
| 1 | 0.82 | 0.65 | 0.51 |
| 2 | 0.73 | 0.54 | 0.23 |
| 3 | 0.43 | 0.34 | 0.28 |
| 4 | 0.41 | 0.21 | 0.31 |
| 5 | 0.68 | 0.43 | 0.24 |
其中,区组 n = 5 n=5 n=5,处理因素水平 g = 3 g=3 g=3, H 0 : μ 1 = μ 2 = μ 3 H_0:\mu_1=\mu_2=\mu_3 H0:μ1=μ2=μ3,即三种不同药物作用后小白鼠肉瘤重量的总体均数相等。
4.3.多个样本均数间的多重比较
当方差分析的结果为拒绝 H 0 H_0 H0,接受 H 1 H_1 H1时,只说明 g g g个总体均数不全相等。若想进一步了解哪两个总体均数不等,须进行多个样本均数间的两两比较或称多重比较。如用两样本均数比较的t检验进行多重比较,将会加大犯 I \mathrm I I型错误的概率。
常见的三种多重比较的方法:
4.3.1.LSD-t检验
即最小显著差异(least significant difference,LSD)t检验,适用于一对或几对在专业上有特殊意义的样本均数间的比较。
4.3.2.Dunnett-t检验
适用于 g − 1 g-1 g−1个实验组与一个对照组均数差别的多重比较。
4.3.3.SNK-q检验
SNK(Student-Newman-Keuls)检验,亦称 q q q检验,适用于多个样本均数两两之间的全面比较。
5.非参数检验之 χ 2 \chi^2 χ2检验
χ 2 \chi^2 χ2检验常用于推断两个总体率或构成比之间有无差异、多个总体率或构成比之间有无差别、多个样本率间的多重比较、两个分类变量之间有无关联性、多维列联表的分析和频数分布拟合优度。
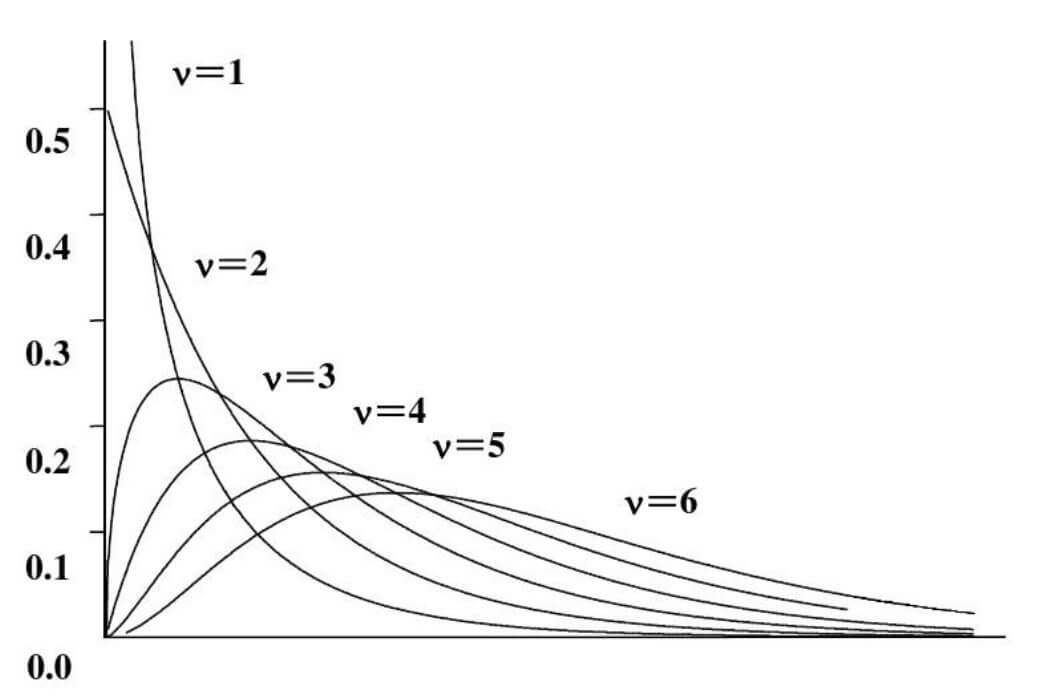
👉 χ 2 \chi^2 χ2分布:
χ 2 \chi^2 χ2分布是一种连续型分布: χ 2 \chi^2 χ2分布只有一个参数,即自由度 v v v。按 χ 2 \chi^2 χ2分布的密度函数 f ( χ 2 ) f(\chi^2) f(χ2)可给出自由度 v = 1 , 2 , 3 , . . . v=1,2,3,... v=1,2,3,...的一簇 χ 2 \chi^2 χ2分布曲线(见上图)。由 χ 2 \chi^2 χ2分布曲线可见, χ 2 \chi^2 χ2分布的形状依赖于自由度 v v v的大小:
- 当自由度 v ⩽ 2 v\leqslant2 v⩽2时,曲线呈 L L L形;
- 随着 v v v的增加,曲线逐渐趋于对称;
- 当自由度 v → ∞ v\to \infty v→∞时, χ 2 \chi^2 χ2分布趋近正态分布。
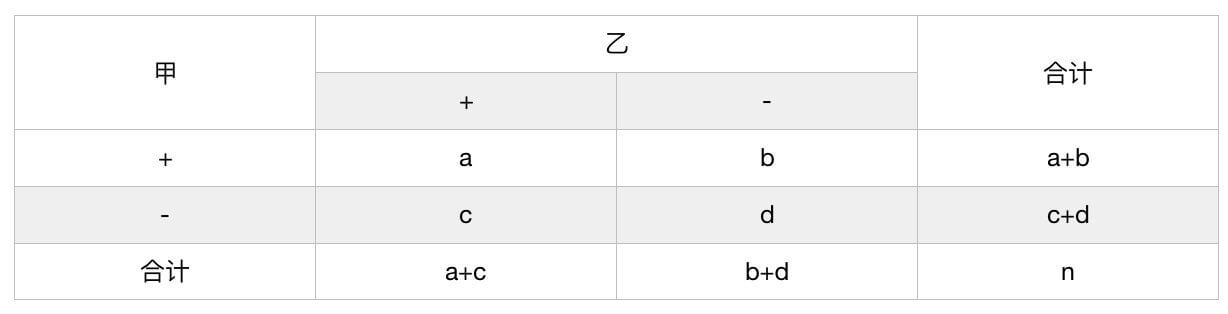
5.1.四格表资料的 χ 2 \chi^2 χ2检验
| 处理组 | 发生数 | 未发生数 | 合计 |
|---|---|---|---|
| 甲 | a a a | b b b | a + b a+b a+b |
| 乙 | c c c | d d d | c + d c+d c+d |
| 合计 | a + c a+c a+c | b + d b+d b+d | n n n |
在比较甲乙两组发生率是否有差别时便可使用 χ 2 \chi^2 χ2检验。
χ 2 = ∑ ( A − T ) 2 T , v = ( 行数 − 1 ) ( 列数 − 1 ) \chi^2=\sum\frac{(A-T)^2}{T},v=(行数-1)(列数-1) χ2=∑T(A−T)2,v=(行数−1)(列数−1)
- A为实际频数
- T为理论频数
其中,
T R C = n R × n C n T_{RC}=\frac{n_R\times n_C}{n} TRC=nnR×nC
- T R C T_{RC} TRC为第 R R R行 C C C列的理论频数
- n R n_R nR为相应的行合计
- n C n_C nC为相应的列合计
上式为通用公式,也可使用四格表专用公式:
χ 2 = ( a d − b c ) 2 n ( a + b ) ( a + c ) ( b + d ) ( c + d ) , v = ( 行数 − 1 ) ( 列数 − 1 ) \chi^2=\frac{(ad-bc)^2n}{(a+b)(a+c)(b+d)(c+d)},v=(行数-1)(列数-1) χ2=(a+b)(a+c)(b+d)(c+d)(ad−bc)2n,v=(行数−1)(列数−1)
5.1.1.四格表资料 χ 2 \chi^2 χ2检验的校正公式
-
当 n ⩾ 40 n\geqslant 40 n⩾40且所有的 T ⩾ 5 T\geqslant 5 T⩾5时,用 χ 2 \chi^2 χ2检验的基本公式或四格表资料 χ 2 \chi^2 χ2检验的专用公式;当 P ≈ α P\approx \alpha P≈α时,改用四格表资料的Fisher确切概率法。
-
当 n ⩾ 40 n\geqslant 40 n⩾40但有 1 ⩽ n < 5 1\leqslant n\lt 5 1⩽n<5时,用四格表资料 χ 2 \chi^2 χ2检验的校正公式: χ 2 = ∑ ( ∣ A − T ∣ − 0.5 ) 2 T \chi^2=\sum\frac{(\mid A-T\mid -0.5)^2}{T} χ2=∑T(∣A−T∣−0.5)2或 χ 2 = ( ∣ a d − b c ∣ − n 2 ) 2 n ( a + b ) ( a + c ) ( b + d ) ( c + d ) \chi^2=\frac{(\mid ad-bc\mid-\frac{n}{2})^2n}{(a+b)(a+c)(b+d)(c+d)} χ2=(a+b)(a+c)(b+d)(c+d)(∣ad−bc∣−2n)2n或改用四格表资料的Fisher确切概率法。
-
当 n < 40 n\lt 40 n<40,或 T < 1 T\lt 1 T<1时,用四格表资料的Fisher确切概率法: P = ( a + b ) ! ( c + d ) ! ( a + c ) ! ( b + d ) ! a ! b ! c ! d ! n ! P=\frac{(a+b)!(c+d)!(a+c)!(b+d)!}{a!b!c!d!n!} P=a!b!c!d!n!(a+b)!(c+d)!(a+c)!(b+d)!直接得到概率值。
5.2.配对四格表资料的 χ 2 \chi^2 χ2检验
配对四格表资料的 χ 2 \chi^2 χ2检验也称为McNemar检验。
- 当 ( b + c ) ⩾ 40 (b+c)\geqslant 40 (b+c)⩾40时: χ 2 = ( b − c ) 2 b + c , v = 1 \chi^2=\frac{(b-c)^2}{b+c},v=1 χ2=b+c(b−c)2,v=1
- 当 ( b + c ) < 40 (b+c)\lt 40 (b+c)<40时,使用校正公式: χ c 2 = ( ∣ b − c ∣ − 1 ) 2 b + c , v = 1 \chi^2_c=\frac{(\mid b-c \mid-1)^2}{b+c},v=1 χc2=b+c(∣b−c∣−1)2,v=1
⚠️卡方检验中四格表和配对四格表的区别:如果是同一组人群,那么就是配对四格表;两组人群互相独立,就是四格表。
5.3.行 × \times ×列表资料的 χ 2 \chi^2 χ2检验
行 × \times ×列表资料的 χ 2 \chi^2 χ2检验用于:
- 多个样本率的比较
- 两个或多个构成比的比较
- 双向无序分类资料的关联性检验
其基本数据有以下3种情况:
- 多个样本率比较时,有R行2列,称为 R × 2 R\times 2 R×2表
- 两个样本的构成比比较时,有2行C列,称 2 × C 2\times C 2×C表
- 多个样本的构成比比较以及双向无序分类资料关联性检验时,有R行C列,称为 R × C R\times C R×C表
专用公式为:
χ 2 = n ( ∑ A 2 n R n C − 1 ) , v = ( 行数 − 1 ) ( 列数 − 1 ) \chi^2=n(\sum\frac{A^2}{n_Rn_C}-1),v=(行数-1)(列数-1) χ2=n(∑nRnCA2−1),v=(行数−1)(列数−1)
5.4.多个样本率间的多重比较
5.4.1.多个实验组间的两两比较
检验水准 α ′ \alpha ' α′用下式估计: α ′ = α ( k 2 ) + 1 \alpha '=\frac{\alpha}{\dbinom{k}{2}+1} α′=(2k)+1α
式中 ( k 2 ) = k ( k − 1 ) 2 \tbinom{k}{2}=\frac{k(k-1)}{2} (2k)=2k(k−1), k k k为样本率的个数。
5.4.2.实验组与同一个对照组的比较
检验水准 α ′ \alpha ' α′用下式估计: α ′ = α 2 ( k − 1 ) \alpha '=\frac{\alpha}{2(k-1)} α′=2(k−1)α
k k k为样本率的个数。
6.秩转换的非参数检验
6.1.配对样本比较的Wilcoxon符号检验
Wilcoxon符号秩检验(Wilcoxon signed-rank test),亦称符号秩和检验。有以下两种用法:
6.1.1.配对样本差值的中位数和0比较
相当于参数检验中的配对样本的t检验
通过一个例子来理解:
对12份血清分别用原方法(检测时间20分钟)和新方法(检测时间10分钟)测谷-丙转氨酶,结果见下表。问两法所得结果有无差别。
| 编号 (1) | 原法 (2) | 新法 (3) | 差值
d
d
d (4)=(3)-(2) | 正秩 (5) | 负秩 (6) |
|---|---|---|---|---|---|
| 1 | 60 | 76 | 16 | 8 | |
| 2 | 142 | 152 | 10 | 5 | |
| 3 | 195 | 243 | 48 | 11 | |
| 4 | 80 | 82 | 2 | 1.5 | |
| 5 | 242 | 240 | -2 | 1.5 | |
| 6 | 220 | 220 | 0 | ||
| 7 | 190 | 205 | 15 | 7 | |
| 8 | 25 | 38 | 13 | 6 | |
| 9 | 198 | 243 | 45 | 9 | |
| 10 | 38 | 44 | 6 | 4 | |
| 11 | 236 | 190 | -46 | 10 | |
| 12 | 95 | 100 | 5 | 3 | |
| 合计 | - | - | - | 54.5 | 11.5 |
H
0
H_0
H0:差值的总体中位数
=
0
=0
=0
H
1
H_1
H1:差值的总体中位数
≠
0
\neq 0
=0
求检验统计量 T T T值:
- 省略所有差值为0的对子数,令余下的有效对子数为n,上题中 n = 11 n=11 n=11;
- 按11个差值的绝对值从小到大编正秩和负秩,遇差值的绝对值相等者取平均秩,称为相同秩(样本较小时,如果相同秩较多,检验结果会存在偏性,因此应提高测量精度,尽量避免出现较多的相同秩);
- 任取正秩和或负秩和为 T T T,上题中 T = 11.5 T=11.5 T=11.5。
当 n ⩽ 50 n\leqslant 50 n⩽50时,可以根据 T T T值进行查表得到相应的 P P P值。
当 n > 50 n\gt 50 n>50时,可用正态近似法作 u u u检验:
u = T − n ( n + 1 ) / 4 n ( n + 1 ) ( 2 n + 1 ) 24 − ∑ ( t j 3 − t j ) 48 u=\frac{T-n(n+1)/4}{\sqrt{\frac{n(n+1)(2n+1)}{24}-\frac{\sum (t^3_j-t_j)}{48}}} u=24n(n+1)(2n+1)−48∑(tj3−tj)T−n(n+1)/4
式中 t j ( j = 1 , 2 , . . . ) t_j(j=1,2,...) tj(j=1,2,...)为第 j j j个相同秩的个数。
6.1.2.单个样本中位数和总体中位数比较
目的是推断样本所来自的总体中位数 M M M和某个已知的总体中位数 M 0 M_0 M0是否有差别。
相当于参数检验中的单样本t检验
通过一个例子来理解:
已知某地正常人尿氟含量的中位数为 45.30 μ m o l / L 45.30\mu mol/L 45.30μmol/L。今在该地某厂随机抽取12名工人,测得尿氟含量见下表。问该厂工人的尿氟含量是否高于当地正常人的尿氟含量?
| 尿氟含量 (1) | (1)-45.30 (2) | 正秩 (3) | 负秩 (4) |
|---|---|---|---|
| 44.21 | -1.09 | 1.5 | |
| 45.30 | 0 | ||
| 46.39 | 1.09 | 1.5 | |
| 49.47 | 4.17 | 3 | |
| 51.05 | 5.75 | 4 | |
| 53.16 | 7.86 | 5 | |
| 53.26 | 7.96 | 6 | |
| 54.37 | 9.07 | 7 | |
| 57.16 | 11.86 | 8 | |
| 67.37 | 22.07 | 9 | |
| 71.05 | 25.75 | 10 | |
| 87.37 | 42.07 | 11 | |
| 合计 | - | 64.5 | 1.5 |
通过正态性检验,该样本总体不服从正态分布,采用Wilcoxon符号秩检验。根据有效差值个数 n = 11 n=11 n=11和 T = 1.5 T=1.5 T=1.5进行查表。
6.2.两个独立样本比较的Wilcoxon秩和检验
相当于参数检验中的两独立样本t检验
求检验统计量T值:
- 把两样本数据混合从小到大编秩,遇数据相等者取平均秩;
- 以样本例数小者为 n 1 n_1 n1,其秩和( T 1 T_1 T1)为 T T T,若两样本例数相等,可任取一样本的秩和( T 1 T_1 T1或 T 2 T_2 T2)为 T T T。
- 当 n 1 ⩽ 10 n_1\leqslant 10 n1⩽10和 n 2 − n 1 ⩽ 10 n_2-n_1\leqslant 10 n2−n1⩽10时,查 T T T界值表。
- 若 n 1 > 10 n_1\gt 10 n1>10或 n 2 − n 1 > 10 n_2-n_1\gt 10 n2−n1>10时,可用正态近似法作 u u u检验。
6.3.完全随机设计多个样本比较的Kruskal-Wallis H检验
相当于方差分析中的完全随机设计
例题:
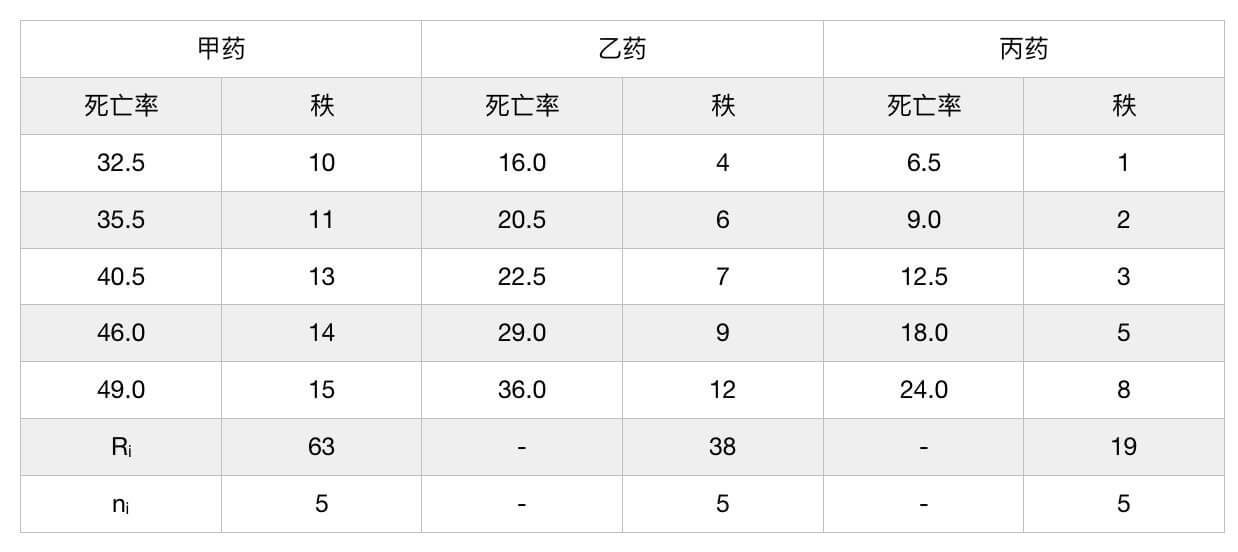
用3种药物灭杀钉螺,每批用200只活钉螺,用药后清点每批钉螺的死亡数、再计算死亡率(%),结果见下表。问3种药物杀灭钉螺的效果有无差别?
求检验统计量 H H H值:
- 把3个样本数据混合从小到大编秩,遇数据相等者取平均秩;
- 设各样本例数为 n i ( ∑ n i = N ) n_i(\sum n_i=N) ni(∑ni=N)、秩和为 R i R_i Ri,按下式求 H H H值: H = 12 N ( N + 1 ) ( ∑ R i 2 n i ) − 3 ( N − 1 ) H=\frac{12}{N(N+1)}(\sum \frac{R_i^2}{n_i})-3(N-1) H=N(N+1)12(∑niRi2)−3(N−1)
- 当各样本数据存在相同秩时,按上式算得的 H H H值偏小,按下式求校正 H C H_C HC值: H C = H / C , C = 1 − ∑ ( t j 3 − t j ) / ( N 3 − N ) H_C=H/C,C=1-\sum(t_j^3-t_j)/(N^3-N) HC=H/C,C=1−∑(tj3−tj)/(N3−N)
- 查表。
若 g = 3 g=3 g=3且最小样本的例数大于5或 g > 3 g\gt 3 g>3时,则 H H H或 H C H_C HC近似服从 v = g − 1 v=g-1 v=g−1的 χ 2 \chi^2 χ2分布,查 χ 2 \chi^2 χ2界值表。
6.3.1.多个独立样本两两比较的 N e m e n y i Nemenyi Nemenyi法检验
当经过多个独立样本比较的Kruskal-Wallis H检验拒绝 H 0 H_0 H0,接受 H 1 H_1 H1,认为多个总体分布位置不全相同时,若要进一步推断是哪两两总体分布位置不同,可用Nemenyi法检验。
6.4.随机区组设计多个样本比较的Friedman M检验
相当于方差分析中的随机区组设计
Friedman M检验,用于推断随机区组设计的多个相关样本所来自的多个总体分布是否有差别。
例题:
8名受试对象在相同实验条件下分别接受4种不同频率声音的刺激,他们的反应率(%)资料见下表。问4种频率声音刺激的反应率是否有差别?
- 区组个数: n = 8 n=8 n=8
- 研究因素的水平个数: g = 4 g=4 g=4
- 总例数: N = n g = 32 N=ng=32 N=ng=32
求检验统计量M值:
- 将每个区组的数据由小到大分别编秩,遇数据相等者取平均秩;
- 计算各样本的秩和 R i R_i Ri,平均秩和为 R ˉ = n ( g + 1 ) / 2 \bar R=n(g+1)/2 Rˉ=n(g+1)/2;
- 按下式求M值。
M = ∑ ( R i − R ˉ ) 2 = ∑ R i 2 − n 2 g ( g + 1 ) 2 / 4 M=\sum(R_i-\bar R)^2=\sum R_i^2-n^2g(g+1)^2/4 M=∑(Ri−Rˉ)2=∑Ri2−n2g(g+1)2/4
若 n > 15 n\gt 15 n>15或 g > 15 g\gt 15 g>15时,超出查表范围,可用 χ 2 \chi^2 χ2近似法,按下式计算 χ 2 \chi^2 χ2值:
χ 2 = 12 M n g ( g + 1 ) C , C = 1 − ∑ ( t j 3 − t j ) n ( g 3 − g ) , v = g − 1 \chi^2=\frac{12M}{ng(g+1)C},C=1-\frac{\sum(t_j^3-t_j)}{n(g^3-g)},v=g-1 χ2=ng(g+1)C12M,C=1−n(g3−g)∑(tj3−tj),v=g−1
👉在机器学习中的应用场景举例:
| 数据集 | 算法A | 算法B | 算法C |
|---|---|---|---|
| D 1 D_1 D1 | 1 | 2 | 3 |
| D 2 D_2 D2 | 1 | 2.5 | 2.5 |
| D 3 D_3 D3 | 1 | 2 | 3 |
| D 4 D_4 D4 | 1 | 2 | 3 |
可按照算法的性能表现(如准确率等)进行编秩。
6.4.1.多个相关样本两两比较的q检验
当经过多个相关样本比较的Friedman M检验拒绝 H 0 H_0 H0,接受 H 1 H_1 H1,认为多个总体分布位置不全相同时,若要进一步推断是哪两两总体分布位置不同,可用q检验。
7.参考资料
- 《医学统计学(第4版)》(人民卫生出版社,主编:孙振球,徐勇勇)
想要获取最新文章推送或者私聊谈人生,请关注我的个人微信公众号:⬇️x-jeff的AI工坊⬇️
个人博客网站:https://shichaoxin.com
GitHub:https://github.com/x-jeff