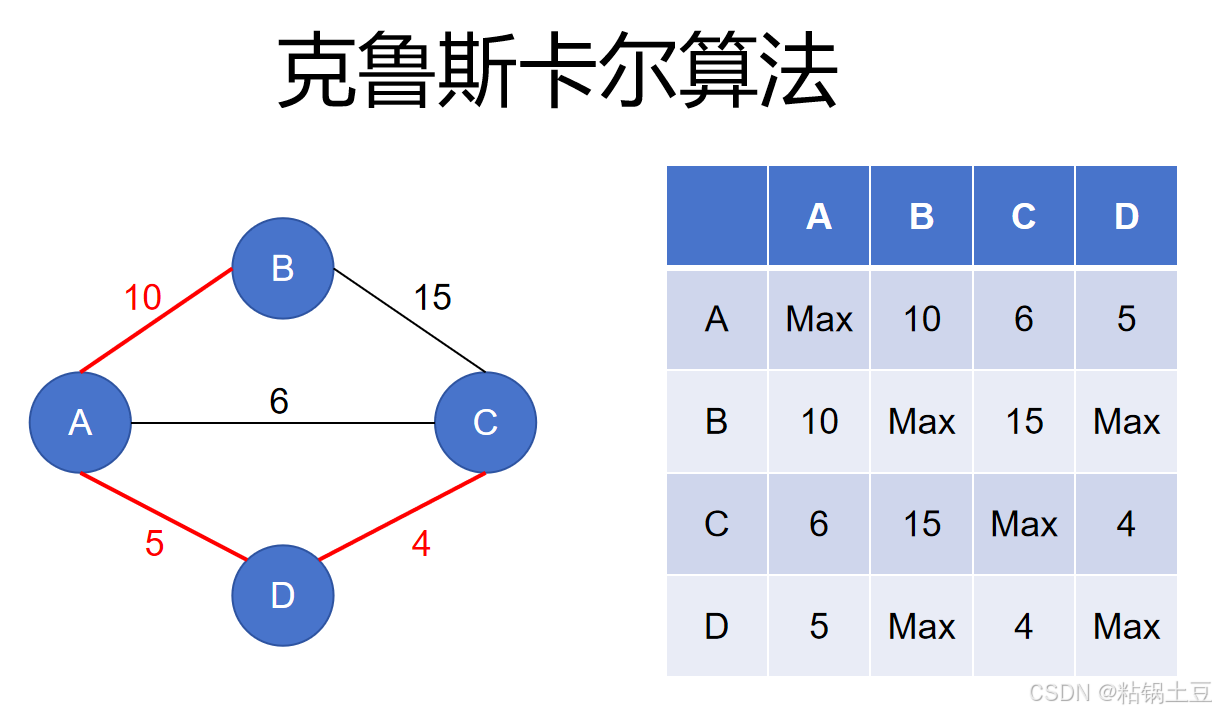
克鲁斯卡尔算法 (加边法)

简介

克鲁斯卡尔算法是一种用于查找最小生成树的算法。以下是该算法的步骤：

1. 找到所有边，并按照权重从小到大排序。
2. 依次遍历边，如果边的两个节点不在一个集合中，则添加这条边，并将两个节点合并到同一个集合中。
3. 如果边的两个节点在同一个集合中，则跳过这条边。
4. 重复步骤2和3，直到所有的节点都在同一个集合中。
   

实现方法

// 定义边的结构，包括起点、终点和权重
class Edge {
  constructor(start, end, weight) {
    this.start = start
    this.end = end
    this.weight = weight
  }
}

// 辅助函数：查找并查集的根节点
function find(parent, i) {
  // 路径压缩
  if (parent[i] === i) {
    return i
  }
  return (parent[i] = find(parent, parent[i]))
}

// 辅助函数：合并两个并查集
function union(parent, rank, x, y) {
  let rootX = find(parent, x)
  let rootY = find(parent, y)

  // 将较小的树合并到较大的树中
  if (rank[rootX] < rank[rootY]) {
    parent[rootX] = rootY
  } else if (rank[rootX] > rank[rootY]) {
    ;``
    parent[rootY] = rootX
  } else {
    parent[rootY] = rootX
    rank[rootX] += 1
  }
}

// 克鲁斯卡尔算法实现
function kruskalMST(graph) {
  const parent = []
  const rank = []
  const result = [] // 最小生成树的结果
  let i = 0 // 用于遍历边

  // 初始化并查集
  graph.forEach((vertex, index) => {
    parent[index] = index
    rank[index] = 0
  })

  // 按边的权重从小到大排序
  graph.sort((a, b) => a.weight - b.weight)

  // 遍历所有边，构建最小生成树
  while (i < graph.length) {
    const edge = graph[i]
    const rootX = find(parent, edge.start)
    const rootY = find(parent, edge.end)

    // 如果这条边不会形成环，则将其加入结果中
    if (rootX !== rootY) {
      result.push(edge)
      union(parent, rank, rootX, rootY)
    }
    i++
  }

  return result
}

// 示例使用
let graph = [
  new Edge(0, 1, 10),
  new Edge(0, 2, 6),
  new Edge(0, 3, 5),
  new Edge(1, 3, 15),
  new Edge(2, 3, 4),
]

const mst = kruskalMST(graph)
function printMST(mst) {
  console.log('Edge \tWeight')
  for (let i = 0; i < mst.length; i++) {
    console.log(mst[i].start + ' - ' + mst[i].end + '\t' + mst[i].weight)
  }
}
// 打印最小生成树的边和权重
console.log('最小生成树：', printMST(mst))