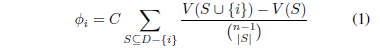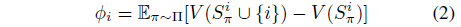Data Shapley: Equitable Valuation of Data for Machine Learning
摘要
随着数据成为推动技术和经济增长的燃料,一个根本性的挑战是如何在算法预测和决策中量化数据的价值。比如,在医疗保健和消费者市场,个人应该为他们产生的数据得到补偿,但不清楚什么是对个人数据的公平估值。在这项工作中,我们开发了一个有原则的框架来处理监督机器学习环境下的数据评估。给定一种基于n个数据点训练的学习算法来生成预测器,我们提出以Data Shapley作为度量指标来量化每个训练数据对预测器性能的影响。Data Shapley独特地满足公平数据估值的几个自然属性。实际中,复杂的学习算法(包括神经网络)是训练在大型数据集,我们用蒙特卡罗和基于梯度的方法来有效地估计Data Shapley值。除了保证公平,在生物医学、图像和合成数据方面的广泛实验表明,数据Shapley还有其他几个好处:(1)它比流行的 leave-one-out 或 leverage score 更强大,能让人们了解哪些数据对给定的学习任务更有价值;(2)低的Shapley值的数据有效的捕获了异常值(outliers)和错误(corruption);(3)高Shapley值的数据告诉我们需要获得什么样的新数据来改进预测器。
1.简介
数据是有价值的,是人工智能力量的来源。在一些领域,如医疗保健和广告,个人生成的数据越来越多地成为市场的一个关键因素,类似于劳动力和资本。有人提出,某些数据构成了个人财产,因此这些个人应该得到补偿,以换取这些数据(Regulation, 2018)。与劳动力和资本一样,一个基本问题是如何公平地评估个人数据。
我们关注监督机器学习在特定环境下的数据评估。为了理解数据的价值,我们的研究需要三个要素:固定的训练数据集、学习算法和性能度量。训练数据是一个固定大小的 n 个数据点的集合,{xi,yi}1n,xi是特征,yi是标签。至于我们的目标,让一个学习算法A接受一个任意的训练集并生成一个预测器。比如,A可以是常见的经验风险最小化程序,其解决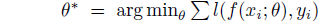
我们需要研究两个问题:(1)什么是每个(xi,yi)的值,在学习算法 A 的性能指标V的各个方面的一个公平的度量;(2)我们如何有效地计算特定情况下的数据值。比如,我们从 N=1000 个病人得到了数据,我们训练一个小的神经网络得到一个小的心脏病分类器。我们也有一些独立的指标来评估训练好的分类器的性能——例如,它在测试集上的预测精度。然后,我们将量化每个患者的数据对分类器在这项任务中的性能的价值。
注意,我们没有为数据定义一个通用值。相反,每个数据的值取决于学习算法、性能度量以及训练集中的其他数据。这种依赖性在机器学习中是合理的,也是可取的。如果我们训练逻辑回归而不是神经网络,一些数据点可能更重要。类似地,如果性能指标变化——如,回归到心脏病发病年龄而不是心脏病发病率——然后一些患者数据的值可能会变。此外,性能指标可以根据不同于训练数据的人口/分布来计算;我们对如何做到这一点没有任何假设。
一个通用的评估数据性能的方法是leave-one-out(LOO)test:比较在整个数据集上训练的预测器性能与在减去一点的整个数据集上训练的预测器性能之间的差异。衡量这一点“值”的一项指标的性能下降。LOO通常用杠杆或影响力评分来估计,用于衡量当一个点的权重发生轻微变化时,预测器会如何变化。我们将在下面的文章中说明,LOO不能满足我们所期望的对数据进行公平估值的自然属性,而且在实验中表现很差。为什么LOO失败的一个简单直观的例子,假设我们的预测器是一个最近邻分类器——也就是说,对于每个测试点,我们在训练集中找到它的最近邻,并为其分配标签。此外,假设每个训练点在训练集中都有两个完全相同的副本。从数据集中移走一个点不会改变预测器,因为其副本依然还在。因此,LOO方法会给每个训练数据点赋值为0,不管实际预测器的性能如何。这个简单的例子说明LOO不能捕获数据子集间潜在的复杂关系。我们提出的data Shapley value通过精确解释这样的关系,提供了更有意义的估值。
我们的贡献
我们提供了在机器学习中公平地评估数据的一个自然的公式。我们利用博弈论的强大结果,提出了数据的Shapley值来量化单个数据点对学习任务的贡献。Data Shapley唯一地满足公平估值的三个自然属性。此外,我们的实证研究表明,数据Shapley还有几个额外的实用功能:1)它与通常的LOO分数相比,提供了更多的观察每个数据点的重要性的见解;2)识别异常值和损坏数据;3)它可以告诉我们如何获取未来的数据来改进预测器。
2. 关于机器学习的公平数据评估
预先准备 D = {(xi,yi)}1n为固定的训练集。我们没有对D做任何分布假设,且数据没必要独立。yi是类别,或者是用于分类和回归的实数。A是算法。我们将A看做一个黑盒,输入大小为0到无穷的训练数据集,返回一个预测器。我们对在数据子集S(S是D的子集)上训练的预测器很感兴趣。性能得分V是另一个黑盒,它以任一预测器为输入,返回一个分数。我们用V(S,A)或V(S)表示在数据集S上训练的预测器的性能。我们的目标是计算一个data value ψi(D,A,V)∈R,一个关于D,A,V的函数,用于量化第 i 个数据的值。我们通常简单记其为 ψi(V)或 ψi。为了方便我们有时会重载S和D的符号,这样它也可以表示一组索引——比如,i ∈ S,如果(xi,yi)在S子集中,且D = (1,……,n)。
例子假设 yi 是二元的,A对应于一个逻辑回归算法——如,A输入任何数据集,为数据集返回一个与其合适的逻辑回归预测器。得分V可以是在单独的数据集上的0/1精度。V(S)是当在子集S上训练逻辑回归器时,0/1测试精度。如果S≠∅,V(S)是一个随机初始化的分类器的性能。通常,用来计算V的测试数据可能来自不同于D的分布。
数据验证的公平属性为了公平,ψ应该满足下面几个属性:
- 如果将(xi,yi)加入训练数据的任一子集中,没有改变算法性能,那么它应该被赋值为 0 。更精确点,假设所有 S⊆D-{i},V(S)=V(S∩{i}),那么 ψi=0。
- 如果对数据i,j和子集S⊆D-{i,j},都有V(S∪{i})=V(S∪{j}),那么 ψi= ψj。总之,如果i和j被加入训练数据的任一子集中时,总是在预测器的得分上产生完全相同的变化,那么由对称性知,i和j应该得到相同的值。
- 在大多数ML的设置中, V = − ∑ k ϵ t e s t s e t l k V = -\sum _{k\epsilon test set}l_{k} V=−kϵtestset∑lklk是预测器在第k个测试点上的损失(我们用负号,使高的得分有低的损失)。定义Vk = -lk,表示预测器在第k个测试点上的性能。类似于ψi(Vk)量化了第i个训练数据在第k个测试数据上的值。如果数据i对测试点1和2的预测分别贡献了ψi(V1)和ψi(V2),那么我们期望i在预测两个测试点时的值——如,当V=V1+V2时,有ψi(V) =ψi(V1)+ψi(V2)。换句话说:当总体预测得分是K个独立预测的和时,数据的值应该是每个预测的值的和。形式上:ψi(V +W) =ψi(V)+ψi(W)表示性能分数V和W。
虽然还有其他值得讨论的数据估值的理想属性,但上面列出的这三个属性实际上将ψi确定为比例常数。
命题2.1 对任何ψ(D,A,V)要满足上面的三个属性,必须有这样的形式:
ψi为数据i的 Shapley值,是在D的所有不含i的子集上的一个求和,C是任意常量。
基本上,v(S)是子集S中的参与者一起工作的奖励。Shapley提出了一种在n个玩家中分配分数的方法,这样每个玩家都能获得公平的报酬,其中公平通过属性来编码,这些属性在数学上等价于我们列出的三个属性。我们可以把数据估值看作一个合作博弈:每个训练数据都是一个参与者,训练数据通过学习者A协同工作,实现预测得分v = V。Shapley值类似于每个玩家收到的支付。
C的选择是任意的,不影响我们的任何实验和分析。
数据Shapley的解释 Eq.1 能被视作对i的所有可能的“边界贡献”的加权求和;权重是子集大小的倒数,子集S属于D - { i }。这个公式与LOO很接近, 只是在这里考虑最后的边际贡献V(D) - V(D - { i }),我们考虑每个点的边际贡献时,假设不是整个训练集,而是它的一个随机子集。换句话说,这个方案中,我们假设不是训练数据,而是它的一个随机子集;Shapley公式通过捕获所有这些可能的子集场景来输出一个公平的值。
3. 估算数据的Shapley
如上面的章节所讨论,Shapley公式(Eq.1)对数据点提供一个公平的值分配。但是,计算Shapley需要计算所有可能的边界贡献,其在训练数据大小上成指数级增长。另外,对每个S⊆D,计算V(S)涉及到使用学习算法A在S上学习一个预测器。因此,对实际的数据集计算精确的Shapley值是困难的。在本节中,我们将讨论估算数据Shapley值的近似方法。
3.1 估算Shapley值
如前所述,Shapley值的计算在数据点n的数量上具有指数复杂度。在这里,我们讨论两种绕过这个问题的方法:
蒙特卡罗方法:
通过设置 C 为
C
=
1
/
n
!
C=1/n!
C=1/n!,我们将 Eq.1 重写为一个等价的公式。∏ 为所有数据点的 n! 排列的一致分布,有:
S
π
i
S_{π}^{i}
Sπi是排列 π 中数据 i 之前的数据点集合。如果 i 是第一个数据,
S
π
i
S_{π}^{i}
Sπi=∅。
如 Eq. 2所述,Shapley值的计算可以表示为一个期望计算问题。因此,通过发展和分析蒙特卡罗方法来估计Shapley值。首先,我们对数据点的随机排列进行采样。然后,扫描从第一个元素到最后一个元素的排列,计算每个新数据点的边际贡献。在多个蒙特卡罗排列上重复相同的过程,最终对数据Shapley的估计只是所有计算出的边际贡献的平均值。这种蒙特卡罗抽样给出了数据Shapley的无偏估计。在实践中,我们生成蒙特卡罗估计,直到平均经验收敛。之前的工作分析了Shapley值的蒙特卡罗近似的误差边界。附录A中的图6描述了数据Shapley收敛的例子。在实际应用中,在n阶上,随着样本个数的增加达到收敛;通常,3n个蒙特卡罗样本是足够收敛的。
截断法:
在机器学习设置,S ⊆ N时,V (S) 通常是用S学得的模型在一个单独测试集上的预测性能。因为测试集是有限的,V (S)本身是训练模型在测试集上的真实性能的近似。在实践中,将数据Shapley值估计到V (S)中的固有噪声就足够了,而V (S)中的固有噪声可以通过测量同一预测器在测试集的bootstrap samples(有放回抽样集)中的性能变化来量化。另一方面,随着S的大小的增加,只增加一个训练点对性能的影响会越来越小。将这两个观察结果结合起来,就得到了一种自然截断方法。
我们可以根据V中的采样变化定义一个“性能容忍度”。当我们扫描采样排列计算边界贡献时,只要V(S)在V(D)的性能容忍度内,我们截断一个采样排列中的边界贡献的计算,且对该分布中所有剩余数据点的边界分布置为0。附录B显示了截断可以在不引入显著估计偏差的情况下节省大量的计算量。在本文的其余部分,我们将截断与蒙特卡罗的组合称为**“截断式蒙特卡罗沙普利”(TMC-Shapley)**;在算法1中有更详细的描述。
3.2 估算性能矩阵V
对每个 S ⊆ D,计算 V(S)需要S学习一个新模型。对一个小的数据集D和一个快的算法A——eg.逻辑回归,LASSO——它可能使用 TMC-Shapley 方法。但是,当数据集较大或预测模型需要较高的计算能力时(eg.深度神经网络),应用 TMC-Shapley可能相当昂贵。我们提出了两种策略来进一步降低大数据情况下Shapley的计算成本。
Gradient Shapely
对于一类广泛的预测模型,A涉及随机梯度下降的变化,其中随机选择的批次D迭代更新模型参数。在这些情况下,一个简单的逼近完全训练模型的方法是考虑在训练数据上对模型只进行一次训练;换句话说,我们只用一轮D的来训练模型。这种近似很符合算法1的框架:对于一个采样的数据点排列,每次对一个数据点执行梯度下降来更新模型;边际贡献是模型性能的变化。算法2描述了详细细节,我们称之为Gradient Shapley或G-Shapely。为了更好地逼近,我们对学习算法执行超参数搜索来发现一个性能最好的结果。在我们的实验中,一个只经过一轮数据训练的模型的学习率大于经过多轮训练的模型。附录C举了数值例子说明近似G-Shapley方法在实验结果中的有效性。
数据组的值
在许多情况中,为了有更好的鲁棒解释性,或由于训练数据量很大,我们倾向于对一组数据点计算数据的Shapley而不是单个数据。比如,在心脏病预测中,我们可以根据患者的年龄、性别、民族等特点将患者分成离散的箱子,然后对每个箱子的Shapley数据进行量化。在这些情况中,我们可以使用同一个程序(算法1)计算一个组的Shapley值,用分组i替换数据点i。因此,即使数据集很大,如果分组的数量合理,我们能计算分组的Shapley值。
4. 实验与应用
在本节中,我们将演示数据Shapley在真实和合成数据的系统实验中的估计和应用。结果表明,具有高Shapley值的点对模型的性能至关重要,反之亦然。然后,我们讨论了与随机获取新数据相比,获取与高值训练点相似的新数据点的效果。此外,我们还进行了两个实验,实验结果表明,有噪声或标签损坏的数据点会被赋予较低的Shapley值。
最后,我们证明了Shapley值也可以为一组个体提供有用的分数。综上所述,这些实验表明,数据Shapley除了具有公平的属性外,还提供了有意义的值来量化数据的重要性,并可以为后续分析提供信息。考虑到杠杆率和影响力评分寻求近似于LOO,在整个实验中,我们重点比较了Shapley方法和LOO方法的性能。LOO计算的是在有兴趣点的完整数据集和不带兴趣点的完整数据集上训练的模型之间的模型性能差异V。
在接下来的所有实验中,我们都有一个训练集,一个单独的测试集用于计算V,以及一个held-out集用于报告每个图形的最终结果。我们对TMC-Shapley和G-Shapley收敛性判别准则是 1 n ∑ i = 1 n ∣ ϕ i t − ϕ i t − 100 ∣ ∣ ϕ i t ∣ < 0.05 \frac{1}{n}\sum_{i=1}^{n}\frac{|\phi _{i}^{t}-\phi _{i}^{t-100}|}{|\phi _{i}^{t}|}<0.05 n1i=1∑n∣ϕit∣∣ϕit−ϕit−100∣<0.05对所有实验,在4个机器上并行计算Shapley值,用时少于24小时,只有一个模型是一个Conv-Net的实验,在4个GPU并行使用了120小时。应该指出的是,这两种数据Shapley算法都可以并行化到迭代的次数,因此,使用更多的并行机器可以使计算变得更快。
4.1 数据的Shapley用于疾病预测
在本实验中,我们使用了英国Biobank数据集;该任务是利用285个特征预测个体是否会被诊断为乳腺和皮肤恶性肿瘤(ICD10编码C50和C44,二元分类)。为每个任务创建平衡的二进制数据集,我们使用1000个体来完成训练任务。逻辑回归对乳腺癌和皮肤癌预测的检验准确率分别为68.7%和56.4%。通过计算模型的准确性来计算性能,该模型在1000名独立患者的数据上训练得到的。这两项任务的不同精度允许我们研究数据Shapley,以获得或多或少比较准确的分类器。我们首先计算TMC-Shapley、G-Shapley和leave -one -out值。TMC-Shapley在4000次蒙特卡罗迭代中收敛于这两个任务,而G-Shapley经过1500次迭代已经收敛。附录A给出了训练集中随机选择的数据点的收敛例子。
有价值数据的重要性
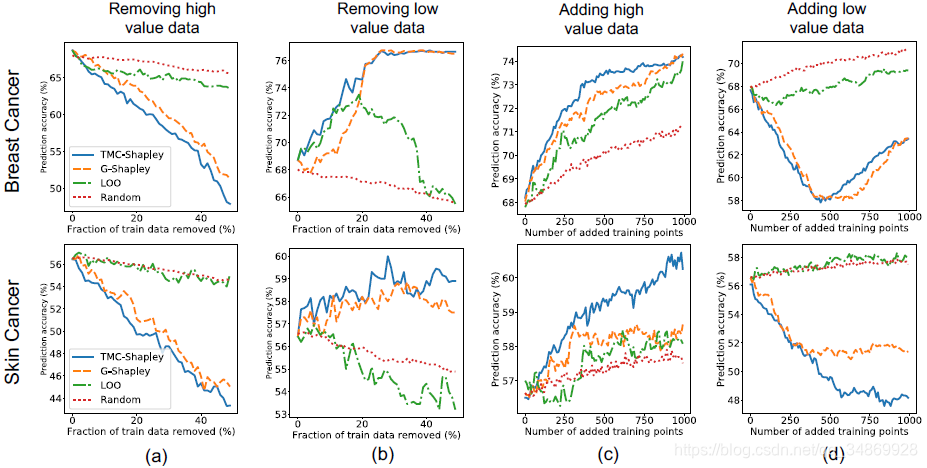
在计算数据值后,我们将训练集中的数据点从最有价值的数据点移到最没有价值的数据点,每次训练一个新的模型。Fig.1(a)显示了丢弃有价值的数据点时性能的变化;Shapley认为有价值的数据点对模型性能至关重要,而LOO估值只比随机估值(即删除随机点)好一点点。Fig.1(b)为相反情况的结果;我们从最没有价值的数据点开始删除数据点。有趣的是,这些训练集中Shapley值较低的点实际上会损害模型的性能,删除这些点将提高准确性。
获得新数据
研究哪种类型的训练数据具有较高的Shapley值,并告诉我们如何通过收集相似的个体来收集新数据,从而提高模型性能。让我们考虑以下实际场景:我们想在训练数据中添加一些新患者,以改进我们的模型。增加一个人是要付出代价的,所以我们必须从2000名候选人中进行选择。我们进行了两个实验:首先我们尝试添加与高值训练点相似的点,然后通过添加低值点重复相同的实验。为此,我们用随机森林回归模型去拟合计算数据Shapley值。该回归模型学习预测那些给定了可观测值的数据点的值。利用训练后的回归模型,我们估计了患者池中患者的价值。Fig.1( c)描述了当我们将高估计值的患者添加到训练集中时,模型性能如何变化;该模型的性能比随机增加新患者更有效。考虑到相反的情况,Fig.1(d)显示,选择错误的患者添加,实际上会损害当前模型的性能。
Figure1. 疾病预测 对于乳腺癌和皮肤癌预测任务,我们使用TMC - Shapley、G-Shapley和leave-one-out (LOO)计算训练集中每个点的值。
(a)我们从训练中删除最有价值的数据,按三种方法加上均匀抽样排列。Shapley方法识别重要的数据点,删除最重要的对TMC -Shapley或G-Shapley有价值的点比随机删除数据的性能差。对于LOO,情况并非如此。
(b)从训练集中移除较低的TMC -Shapley或G-Shapley值数据可以提高预测器的性能。
(c)我们获得的新患者与训练数据中的高TMC -Shapley或G-Shapley值患者相似,与随机增加患者相比,这带来了更大的性能提升。
(d)获得与低TMC-Shapley或G-Shapley值患者相似的新患者没有帮助。
4.2 合成数据
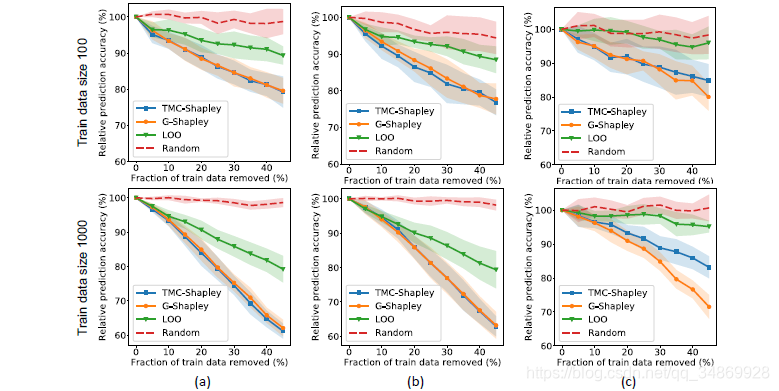
我们使用合成数据进一步分析Shapley值。数据生成过程如下。首先,从50维高斯分布N(0,I)对特征进行采样。然后为每个样本 xi 分配一个二进制标签 yi,其中P(yi = 1) = f(x)表示函数 f( . )。我们创建的数据集:20个数据集是特征-标签的线性关系,线性关系用 f( . )表示, 还有20个数据集的 f( . ) 是一个三阶多项式。对于第一组数据集,我们使用逻辑回归模型;对于第二组数据集,我们同时使用逻辑回归和带有一个隐含层的神经网络。然后我们开始从最有价值的训练点移到最没有价值的训练点,并跟踪模型性能的变化。Fig.2为训练数据大小为100和1000时的结果;对于所有的情况,在决定对模型性能有更积极影响的数据上,Shapley估值方法优于LOO方法。注意,Shapley值总是依赖于所选择的模型:在具有非线性特征-标签关系的数据集中,能够提高非线性模型性能的数据点对线性模型是有害的,因此没有价值。
Figure 2. 合成实验 将显示三种不同情况的平均结果。纵轴为相对精度,用精度除以在不进行删除的整个训练数据上的训练的模型的精度。每个图使用20个数据集。所有的数据集生成过程如下:输入特征 x,生成标签,p (y|x) = f (x)。 (a) 中的 f( . )是线性的,(b)中的 f( . )是一个三阶多项式,( c)和(b)使用相同的数据集。(a)和(b) 的模型是逻辑回归模型,( c)的模型是神经网络。这两种Shapley方法都能更好地为数据点分配值,给那些对模型有高的积极影响的数据点赋高值。彩色阴影区域表示20组数据结果的标准偏差。
4.3 标签噪音
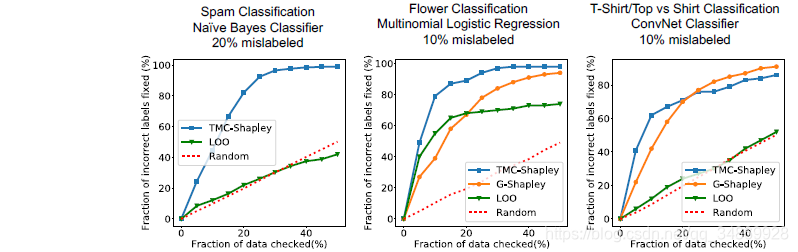
使用众包对数据打标签容易出错,而错误标记的数据是一种简单的数据中毒方法。在本实验中,给定一个带有噪声标签的训练数据,我们通过检查从最无价值的数据点到最有价值的数据点来检查和纠正错误标签的例子,因为我们期望错误标签的例子是在最无价值的点中(一些Shapley值为负)。Fig.3 显示了该方法的有效性,该结论是通过TMC-Shapley、Gradient-Shapley(如果适用)和LOO方法与随机检验基准进行比较的得到的。我们对三个不同的数据集和三个不同的预测模型进行了实验。在第一个实验中,我们使用垃圾邮件分类数据集(Metsis et al., 2006),使用3000个数据点训练一个多项式朴素贝叶斯模型(Multinomial Naive Bayes model),该模型以电子邮件的单词表示包作为输入。我们随机翻转标签得到20%的训练点数。TMC-Shapley在5000次迭代中收敛。在接下来的实验中,我们使用了5个不同类别的花卉图像分类数据集。我们通过 Inception - v3 模型对花卉图像进行传递,并在学习网络中1000幅图像上训练一个多项式逻辑回归模型,其中10%的图像被错误标记。这两种Shapley算法在2000次迭代中收敛。最后,我们在1000张Fashion MNIST数据集的图像上训练了卷积神经网络,用来对t恤和上衣进行分类,该网络包括一个卷积层和两个前向传播层,其中10%的数据点翻转了标签。TMC-Shapley和G-Shapley都在2000次迭代中收敛。该值是在大小为1000的单独集上计算的。Fig.3 显示了结果。Fig.4 显示了花卉和Fashion MNIST数据集中TMC-Shapley值最小的5张图片,这些图片都是被错误地标记的示例。
Figure 3. 纠正翻转标签 我们从最没有价值的点到最有价值的点,检查训练数据点,并修复错误标记的例子。结果表明,Shapley值方法能够最早地检测出错误标记的例子。在Logistic回归模型中,LOO的效果较好,但在其他两个模型中,LOO的性能与随机检验相似。
Figure 4. 标签噪音和Shapley值 所有Shapley值小的图片都被错误标记
4.4 数据质量和价值
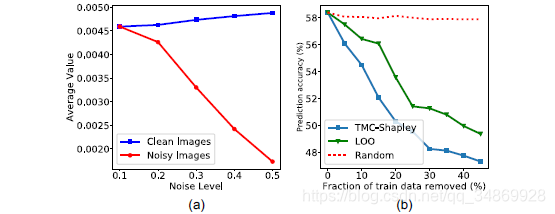
在这个实验中,我们使用了Dog vs. Fish数据集。对于每个类,从Imagenet中提取1200幅图像。我们使用了最新的 Incep -v3 网络,除了顶层外,所有层都是冻结的。随机抽取100幅图像作为训练集,用1000幅图像计算值函数。我们通过添加白噪声来破坏10%的训练数据,计算干净和有噪声图像的 TMC - Shapley平均值,并在不同噪声水平下重复相同的实验。如 Fig.5(a) 所示,随着噪声水平的增加(数据质量下降),噪声图像的数据Shapley值减小。
Figure 5. (a)数据质量和价值:白噪声增加到10%的训练点数。随着噪声水平的提高,噪声图像的平均 TMC - Shapley 值相对于干净图像有所降低。(b)分组的Shapley值:删除有价值的组比删除LOO得分最高的组更能降低性能。
4.5 分组的Shapley值
在本实验中,我们使用医院再入院数据集的一个平衡子集对患者的再入院情况进行二元预测。我们将患者按性别、种族和年龄的人口统计学特征交叉分为146组。在大小为60000,精度为58.4%的训练集上训练一种梯度提升分类器(gradient boosting classifier)。然后计算分组的TMC - Shapey值。Fig.5(b) 显示,最有价值的组也是模型性能最重要的组。除了计算效率外,分组的Shapley的一个重要优点是易于解释。例如,在这个数据集中,老年患者的群体比年轻患者更有价值,少数族裔患者的价值更低,女性群体在Shapley的数据上往往比男性更有价值,等等。
5. 相关工作
Shapley value是在博弈论的经典论文(Shapley, 1953)中提出的,在经济学中有着广泛的影响。它被应用于分析和建模各种问题,包括投票、资源分配和讨价还价等。据我们所知,Shapley值还没有被用来量化像我们这样的机器学习环境中的数据价值。Shapley值最近被提出作为解释黑盒预测模型的特征重要性评分。他们的目标是量化给定的预测,哪些特性对模型输出影响最大。我们的目标非常不同,我们的目标是量化单个数据点的价值(而不是特性)。也有文献关于使用蒙特卡罗方法,网络近似,以及分析求解,估计在特定情况下的Shapley值。
在线性回归中,Cook’s Distance度量删除一个点对回归模型的影响。杠杆和影响是相关的概念,衡量扰动每个点如何影响模型参数和对其他数据的模型预测。然而,这些方法不满足任何公平条件,也被证明有鲁棒性问题。在广泛的讨论中,经济学家和政策制定者一直在热烈讨论数据的价值以及个人应如何获得补偿,同时也在讨论如何激励参与者生成有用的数据。
6. 讨论
我们提出数据Shapley作为一个公平的框架来量化学习算法中个体训练数据的价值。数据Shapley唯一满足公平数据估值的三个自然属性。有些ML设置可能不需要这些属性,并且可能需要添加其他属性。清楚地理解这些不同的场景,并研究适当的数据价值概念,是未来工作的一个非常重要的方向。根据经济学的联系,我们认为我们列出的这三个属性是一个合理的起点。虽然我们的实验展示了Shapley数据的几个理想特性,但是我们应该小心地解释它。由于篇幅的限制,我们忽略了许多关于个人数据内在价值的重要考虑,我们关注的是在非常具体的监督学习算法训练集上下文中的估值。我们承认数据的价值的细微差别——如,隐私,个人关联——不被我们的框架捕获。此外,我们并不建议人们应该通过他们的数据Shapley值得到确切的补偿;我们相信Shapley提供的数据对于定量的洞察更有用。
在数据Shapley框架中,个体数据的值取决于学习算法、评价指标以及训练集中的其他数据点。因此,当我们讨论Shapley值高(或低)的数据时,我们假设所有这些上下文都是给定的。如果上下文发生变化,对一个上下文没有价值的数据可能非常有价值。了解数据Shapley对不同学习功能和度量的行为是后续工作的一个有趣方向。