十、非参数检验：使用python进行卡方拟合优度检验

在参数检验中都是假设总体服从正态分布，那么如何才能知道总体在理论上服从一个什么分布呢？卡方拟合优度检验就是用来检验总体是否服从某个指定分布。从而可以进行：

检测观察数与理论数之间的一致性；
通过检测观察数与理论数之间的一致性来判定事物之间的独立性。

1. 卡方拟合优度检验的原理

1.1. 假设检验的形式

$H_0: 总体服从某个分布 \quad H_1: 总体不服从某个分布$

1.2. 进行假设检验的步骤

在 $H_0$ 下，总体X取值的全体分成k个两两不相交的子集 $A_1,....A_k$ ;
以 $O_i(i=1,...,k)$ 记录样本观察值 $x_1,...,x_n$ 中落在 $A_i$ 的个数（观察频数）
当 $H_0$ 为真且分布完全已知时，计算事件 $A_i$ 发生的概率 $p_i=P(A_i), i =1, ..., k$ ; 如果假设的分布还有r个未知参数时，要先利用参数估计这r个未知参数，然后求得 $p_i$ 的估计 $\hat p_i$ ;
计算理论频数 $T_i=np_i(n\hat p_i)$
构造检验统计量，道理上来说就是要检测 $O_i与T_i$ 差异的显著性，构造如下检验统计量：
$\chi^2=\sum_{i=1}^k\frac{(O_i-T_i)^2}{T_i}$
当假设分布不含有任何未知数时，服从自由度为 $k - 1$ 的卡方分布；当假设分布含有 $r$ 个未知参数时，该统计量服从自由度为 $k - r - 1$ 的卡方分布。

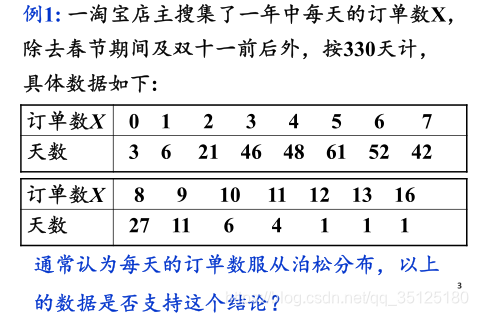
1.3. 实例

在这里插入图片描述
解：由于泊松分布含有一个未知参数 $\lambda$ , 所以首先使用极大似然估计知道其估计为样本均值， $\hat \lambda=1749/330=5.3$
使用python计算如下：

import numpy as np
import pandas as pd
from scipy import stats

d = {'order_counts': list(range(14))+[16], 'o_days':[3,6,21,46,48,61,52,42,27,11,6,4,1,1,1]}
df = pd.DataFrame(d)

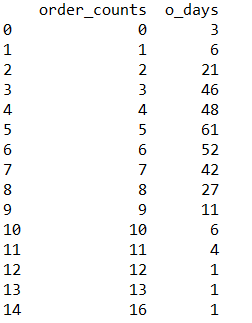
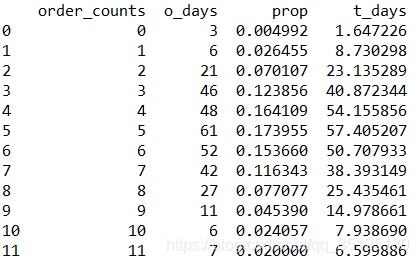
此时，使用基本数据构建的数据框输出如下：
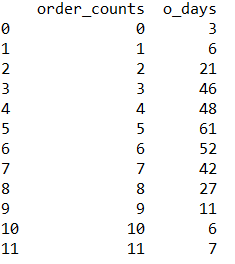
在这里插入图片描述
因为每天订单数大于11的天数很少，所以将其合并，也就是每天不少于11个订单的天数为7, python处理如下：

df.iloc[11,1]=7
df=df[:12]

此时，数据如下：
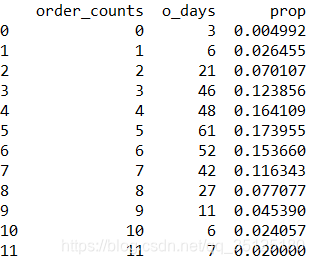
在这里插入图片描述
接下来根据原假设成立，计算理论频率：

Poiss=stats.poisson(mu=5.3)
df['prop']=Poiss.pmf(df['order_counts'])
# 修正订单数大于11对应的概率
df.iloc[11, 2]=1-Poiss.cdf(10)

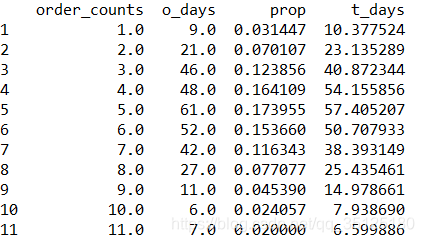
此时的输入如下：
在这里插入图片描述
接下来计算理论频数：

df['t_days']=330*df['prop']

得到的数据如下：
在这里插入图片描述
在卡方拟合优度检验中，一般要求 $n\gt 50, np_i\gt 5$ . 所以要对理论频数不满足要求的行累计的后面的行。但是还有一种情况，就是末尾的数据通过计算后，不满足理论频数的要求，要与前面的行合并。处理如下：

df1=pd.DataFrame(df)
n=None
for i in range(len(df1)):
    if df1.iloc[i,3] < 5:
        n =i
        df1.iloc[i+1,:] = df1.iloc[i+1,:] + df1.iloc[i,:]
    else:
        break
if n is not None:
    df1 = df1.iloc[n+1:,:]

上面的代码可以自动完成从前往后遍历数据框，遇到理论频数不满足要求的情况进行处理。因为本例题后面行的数据没有出现理论频数不满足要求的情况，所以没有编写处理的代码。进过上面的处理，目前数据如下：
在这里插入图片描述
至此，我们就可以使用scipy模块的函数chisquare进行验证，代码如下：

stats.chisquare(df1['o_days'], df1['t_days'], ddof=1)
# 输出结果
Power_divergenceResult(statistic=3.9705897417232916, pvalue=0.9133375422858901)

因为 $\gt \alpha=0.05$ ,所以我们接受原假设，即认为这些数据来自一个泊松分布的总体。

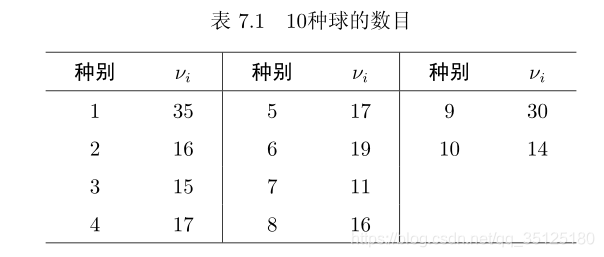
例2: 某箱子中盛有10种球，现在从中有返回地随机抽取200个，其中第 $i$ 种球共取得 $v_i$ 个，数据记录如下。
在这里插入图片描述
问箱子中这10种球的比例是否一样?( $\alpha=0.05$ )
解： $H_0: 10种球比例一样$
python计算如下：

import numpy as np
import pandas as pd
from scipy import stats
d={'o_vals':[35,16,15,17,17,19,11,16,30,14]}
df = pd.DataFrame(d)
df['t_vals']=[200*1/10]*len(df)

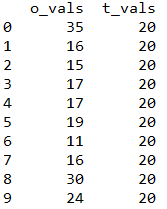
这样我们就得到了为进行卡方拟合优度检验所需的数据，如下：
在这里插入图片描述
继续使用python做出分析：

stats.chisquare(df['o_vals'], df['t_vals'])
# 结果：
Power_divergenceResult(statistic=24.900000000000002, pvalue=0.0030838136870983547)

因为 $pvalue=0.0030838136870983547\lt \alpha=0.05$ ,所以拒绝原假设，认为箱子中10种球的比例是不一样的。