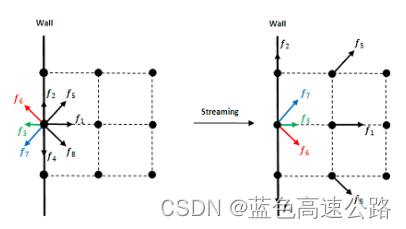
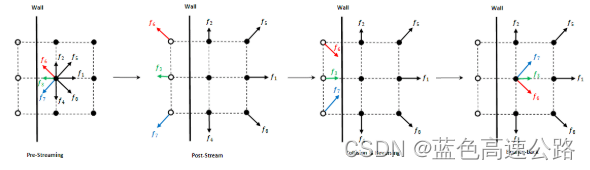
基于上篇D2Q9实现D3Q19。
from numpy import *
from numba import jit
from tqdm import tqdm
雷诺数(Re)是反应粘性和惯性之间平衡的无量纲数。
R
e
=
u
L
ν
Re = u\frac{L}{\nu}
Re=uνL
流体速度u,特征长度
L
L
L,
ν
\nu
ν流体粘度
低速、高粘度和封闭的流体条件导致低Re,粘性力占主导地位。如果Re<<1,这种流体被称为Stokes或者Creeping flow. 由于孔径小,这种流动在许多多孔介质中的液体中是很常见的。
omega 松弛频率
如果
ω
\omega
ω很小,流体只能缓慢地收敛到其平衡状态:高粘性。
流体的粘性与松弛参数
ω
\omega
ω成反比。
ν
=
δ
t
c
s
2
(
1
ω
−
1
2
)
\nu=\delta t c_{s}^{2}\left(\frac{1}{\omega}-\frac{1}{2}\right)
ν=δtcs2(ω1−21)
其中,
c
s
2
=
1
3
c_{s}^{2}=\frac{1}{3}
cs2=31
maxIter = 200000 # 迭代次数
Re = 20 # 雷诺数
uLB = 0.04 # 模型的入口速度
nx, ny, nz = 40, 20, 20 # x, y轴长度
ly = ny-1 # 用于计算入口,为模型增加扰动,当雷诺数较小时,计算缺少扰动
cx, cy, cz, r = nx//4, ny//2, nz//2, nx//9 # 圆柱坐标
nulb = uLB*r/Re # 粘性系数
omega = 1/(3*nulb+0.5) # 松弛频率
t i t_i ti 用于补偿不同长度的速度
流入条件
密度
//face1 //face2 //face3
* * * * *
* * * * * * * * *
* * * * *
1 5 8 11 15
0 2 4 6 9 12 14 16 18
3 7 10 13 17
因为
ρ ( x , t ) = ∑ i = 0 18 f i i n ( x , t ) \rho(\boldsymbol{x}, t)=\sum_{i=0}^{18} f_{i}^{\mathrm{in}}(\boldsymbol{x}, t) ρ(x,t)=i=0∑18fiin(x,t)
u ( x , t ) = 1 ρ ( x , t ) δ x δ t ∑ i = 0 18 v i f i i n ( x , t ) \boldsymbol{u}(\boldsymbol{x}, t)=\frac{1}{\rho(\boldsymbol{x}, t)} \frac{\delta x}{\delta t} \sum_{i=0}^{18} \boldsymbol{v}_{i} f_{i}^{\mathrm{in}}(\boldsymbol{x}, t) u(x,t)=ρ(x,t)1δtδxi=0∑18vifiin(x,t)
定义
ρ 1 = f 0 + f 1 + f 2 + f 3 + f 4 ( unknown ) ρ 2 = f 5 + f 6 + f 7 + f 8 + f 9 + f 10 + f 11 + f 12 + f 13 (known) ρ 3 = f 14 + f 15 + f 16 + f 17 + f 18 ( known ) \begin{aligned} &\rho_{1}=f_{0}+f_{1}+f_{2}+f_{3}+f_{4}(\text { unknown }) \\ &\rho_{2}=f_{5}+f_{6}+f_{7}+f_{8}+f_{9}+f_{10}+f_{11}+f_{12}+f_{13} \text { (known) } \\ &\rho_{3}=f_{14}+f_{15}+f_{16}+f_{17}+f_{18}(\text { known }) \end{aligned} ρ1=f0+f1+f2+f3+f4( unknown )ρ2=f5+f6+f7+f8+f9+f10+f11+f12+f13 (known) ρ3=f14+f15+f16+f17+f18( known )
同时
ρ = ρ 1 + ρ 2 + ρ 3 ρ u x = ρ 1 − ρ 3 \begin{aligned} &\rho=\rho_{1}+\rho_{2}+\rho_{3} \\ &\rho u_{x}=\rho_{1}-\rho_{3} \end{aligned} ρ=ρ1+ρ2+ρ3ρux=ρ1−ρ3
u x u_x ux速度 x x x方向的分量
因此
ρ = ρ 2 + 2 ρ 3 1 − u x \rho=\frac{\rho_{2}+2 \rho_{3}}{1-u_{x}} ρ=1−uxρ2+2ρ3
rho[0,:,:] = 1/(1-u[0,0,:,:])*(sum(fin[col2,0,:,:],axis=0)+2*sum(fin[col3,0,:,:],axis=0))
流入侧f0 f1 f2 f3 f4的密度分布函数
E ( i , ρ , u ) = ρ t i ( 1 + v i ⋅ u c s 2 + 1 2 c s 4 ( v i ⋅ u ) 2 − 1 2 c s 2 ∣ u ∣ 2 ) E(i, \rho, \boldsymbol{u})=\rho t_{i}\left(1+\frac{\boldsymbol{v}_{\boldsymbol{i}} \cdot \boldsymbol{u}}{c_{s}^{2}}+\frac{1}{2 c_{s}^{4}}\left(\boldsymbol{v}_{\boldsymbol{i}} \cdot \boldsymbol{u}\right)^{2}-\frac{1}{2 c_{s}^{2}}|\boldsymbol{u}|^{2}\right) E(i,ρ,u)=ρti(1+cs2vi⋅u+2cs41(vi⋅u)2−2cs21∣u∣2)
密度总是接近于他们的平衡状态。
首先将未知密度分布函数初始化为其平衡值。
随后,检查相反分布函数偏离平衡的程度,再加上这个值作为修正。
f 0 i n = E ( 0 , ρ , u ) + ( f 18 i n − E ( 18 , ρ , u ) ) f 1 i n = E ( 1 , ρ , u ) + ( f 17 i n − E ( 17 , ρ , u ) ) f 2 i n = E ( 2 , ρ , u ) + ( f 16 i n − E ( 16 , ρ , u ) ) f 3 i n = E ( 3 , ρ , u ) + ( f 15 i n − E ( 15 , ρ , u ) ) f 4 i n = E ( 4 , ρ , u ) + ( f 14 i n − E ( 14 , ρ , u ) ) \begin{aligned} f_{0}^{\mathrm{in}} &=E(0, \rho, \boldsymbol{u})+\left(f_{18}^{\mathrm{in}}-E(18, \rho, \boldsymbol{u})\right) \\ f_{1}^{\mathrm{in}} &=E(1, \rho, \boldsymbol{u})+\left(f_{17}^{\mathrm{in}}-E(17, \rho, \boldsymbol{u})\right) \\ f_{2}^{\mathrm{in}} &=E(2, \rho, \boldsymbol{u})+\left(f_{16}^{\mathrm{in}}-E(16, \rho, \boldsymbol{u})\right) \\ f_{3}^{\mathrm{in}} &=E(3, \rho, \boldsymbol{u})+\left(f_{15}^{\mathrm{in}}-E(15, \rho, \boldsymbol{u})\right) \\ f_{4}^{\mathrm{in}} &=E(4, \rho, \boldsymbol{u})+\left(f_{14}^{\mathrm{in}}-E(14, \rho, \boldsymbol{u})\right) \end{aligned} f0inf1inf2inf3inf4in=E(0,ρ,u)+(f18in−E(18,ρ,u))=E(1,ρ,u)+(f17in−E(17,ρ,u))=E(2,ρ,u)+(f16in−E(16,ρ,u))=E(3,ρ,u)+(f15in−E(15,ρ,u))=E(4,ρ,u)+(f14in−E(14,ρ,u))
fin[[0,1,2,3,4],0,:] = feq[[0,1,2,3,4],0,:] + fin[[18,17,16,15,14],0,:] - feq[[18,17,16,15,14],0,:]
v = array([[1,-1,0], [1,0,1], [1,0,0], [1,0,-1], [1,1,0],
[0,-1,1], [0,-1,0], [0,-1,-1], [0,0,1], [0,0,0], [0,0,-1], [0,1,1], [0,1,0], [0,1,-1],
[-1,-1,0], [-1,0,1], [-1,0,0], [-1,0,-1], [-1,1,0]])
t = array([1/36, 1/36, 1/18, 1/36, 1/36,
1/36, 1/18, 1/36, 1/18, 1/3, 1/18, 1/36, 1/18, 1/36,
1/36, 1/36, 1/18, 1/36, 1/36])
col1 = array([0, 1, 2, 3, 4])
col2 = array([5, 6, 7, 8, 9, 10, 11, 12, 13])
col3 = array([14, 15, 16, 17, 18])
密度
ρ ( x , t ) = ∑ i = 0 18 f i i n ( x , t ) \rho(\boldsymbol{x}, t)=\sum_{i=0}^{18} f_{i}^{\mathrm{in}}(\boldsymbol{x}, t) ρ(x,t)=i=0∑18fiin(x,t)
rho = zeros((nx, ny,nz))
for ix in range(nx):
for iy in range(ny):
for iz in range(nz):
rho[ix, iy, iz] = 0
for i in range(19):
rho[ix, iy, iz] += fin[i, ix, iy, iz]
压力
压力正比于密度,根据理想气体状态方程,在等温气体中
p
=
c
s
2
ρ
p=c_{s}^{2} \rho
p=cs2ρ
在D3Q19模型中
c
s
2
=
1
3
δ
x
2
δ
t
2
c_{s}^{2}=\frac{1}{3} \frac{\delta x^{2}}{\delta t^{2}}
cs2=31δt2δx2
速度
//face1 //face2 //face3
* * * * *
* * * * * * * * *
* * * * *
1 5 8 11 15
0 2 4 6 9 12 14 16 18
3 7 10 13 17
v
0
v_0
v0(1,-1,0),
v
1
v_1
v1(1,0,1),
v
2
v_2
v2(1,0,0),
v
3
v_3
v3(1,0,-1),
v
4
v_4
v4(1,1,0)
v
5
v_5
v5(0,-1,1),
v
6
v_6
v6(0,-1,0),
v
7
v_7
v7(0,-1,-1),
v
8
v_8
v8(0,0,1),
v
9
v_9
v9(0,0,0),
v
10
v_{10}
v10(0,0,-1),
v
11
v_{11}
v11(0,1,1),
v
12
v_{12}
v12(0,1,0),
v
13
v_{13}
v13(0,1,-1)
v
14
v_{14}
v14(-1,-1,0),
v
15
v_{15}
v15(-1,0,1),
v
16
v_{16}
v16(-1,0,0),
v
17
v_{17}
v17(-1,0,-1),
v
18
v_{18}
v18(-1,1,0)
u ( x , t ) = 1 ρ ( x , t ) δ x δ t ∑ i = 0 18 v i f i i n ( x , t ) \boldsymbol{u}(\boldsymbol{x}, t)=\frac{1}{\rho(\boldsymbol{x}, t)} \frac{\delta x}{\delta t} \sum_{i=0}^{18} \boldsymbol{v}_{i} f_{i}^{\mathrm{in}}(\boldsymbol{x}, t) u(x,t)=ρ(x,t)1δtδxi=0∑18vifiin(x,t)
v = np.array([[1,-1,0], [1,0,1], [1,0,0], [1,0,-1], [1,1,0], [0,-1,1], [0,-1,0], [0,-1,-1], [0,0,1], [0,0,0], [0,0,-1], [0,1,1], [0,1,0], [0,1,-1], [-1,-1,0], [-1,0,1], [-1,0,0], [-1,0,-1], [-1,1,0]])
u = zeros((3, nx, ny, nz))
for ix in range(nx):
for iy in range(ny):
for iz in range(nz):
u[0, ix, iy, iz] = 0
u[1, ix, iy, iz] = 0
u[2, ix, iy, iz] = 0
for i in range(19):
u[0,ix,iy,iz] += v[i,0]*fin[i,ix,iy,iz]
u[1,ix,iy,iz] += v[i,1]*fin[i,ix,iy,iz]
u[2,ix,iy,iz] += v[i,2]*fin[i,ix,iy,iz]
@jit
def macroscopic(fin):
rho = sum(fin, axis=0)
u = zeros((3, nx, ny, nz))
for i in range(19):
u[0,:,:,:] += v[i,0] * fin[i,:,:,:]
u[1,:,:,:] += v[i,1] * fin[i,:,:,:]
u[2,:,:,:] += v[i,2] * fin[i,:,:,:]
u /= rho
return rho, u
平衡方程
E
(
i
,
ρ
,
u
)
=
ρ
t
i
(
1
+
v
i
⋅
u
c
s
2
+
1
2
c
s
4
(
v
i
⋅
u
)
2
−
1
2
c
s
2
∣
u
∣
2
)
E(i, \rho, \boldsymbol{u})=\rho t_{i}\left(1+\frac{\boldsymbol{v}_{\boldsymbol{i}} \cdot \boldsymbol{u}}{c_{s}^{2}}+\frac{1}{2 c_{s}^{4}}\left(\boldsymbol{v}_{\boldsymbol{i}} \cdot \boldsymbol{u}\right)^{2}-\frac{1}{2 c_{s}^{2}}|\boldsymbol{u}|^{2}\right)
E(i,ρ,u)=ρti(1+cs2vi⋅u+2cs41(vi⋅u)2−2cs21∣u∣2)
# 平衡态计算
@jit
def equilibrium(rho, u):
usqr = 3/2 * (u[0]**2 + u[1]**2 + u[2]**2)
feq = zeros((19, nx, ny, nz))
for i in range(19):
cu = 3 * (v[i,0]*u[0,:,:,:] + v[i,1]*u[1,:,:,:] + v[i,2]*u[2,:,:,:])
feq[i,:,:,:] = rho*t[i] * (1 + cu + 0.5*cu**2 - usqr)
return feq
碰撞
f i out − f i in = − ω ( f i in − E ( i , ρ , u ⃗ ) ) f_{i}^{\text {out }}-f_{i}^{\text {in }}=-\omega\left(f_{i}^{\text {in }}-E(i, \rho, \vec{u})\right) fiout −fiin =−ω(fiin −E(i,ρ,u))
fout = fin-omega*(fin-eq)
迁移
for ix in range(nx):
for iy in range(ny):
for iz in range(nz):
for i in range(19):
next_x = ix + v[i,0]
if next_x<0:
next_x = nx-1
if next_x>=nx:
next_y = 0
next_y = iy + v[i,1]
if next_y<0:
next_y = ny-1
if next_y>=ny:
next_y = 0
next_z = iz + v[i,2]
if next_z<0:
next_z = nz-1
if next_z>=nz:
next_z = 0
fin[i,next_x,next_y,next_z] = fout[i,ix,iy,iz]
np.roll(a,shift,axis=None) 将数组a,沿着axis方向,滚动shift长度
可改写成
for i in range(19):
fin[i, :, :, :] = roll(roll(roll(fout[i,:,:,:],v[i,0],axis=0), v[i,1], axis=1), v[i,2], axis=2)
边界条件
Bounce-back BCs
反弹边界条件是处理静止无滑移壁面的一类常用格式,是指当离散分布函数到达边界节点时,将沿着其进入的方向散射回流体,包括on-grid bounce-back(边界与晶格点对齐)和 mid-grid bounce-back(边界在界外节点和界内节点之间的中心)。
on-grid bounce-back
mid-grid bounce-back
f i in ( x , t + 1 ) = f j out ( x , t ) f_{i}^{\text {in }}(x, t+1)=f_{j}^{\text {out }}(x, t) fiin (x,t+1)=fjout (x,t)
v i = − v j v_{i}=-v_{j} vi=−vj
for i in range(19):
fout[i,obstacle] = fin[18-i, obstacle]
def obstacle_fun(x, y, z):
return (x-cx)**2 + (y-cy)**2 + (z-cz)**2 < r**2
fromfunction从函数中创建数组,返回数组,符合条件值为True,不符合为False。
obstacle = fromfunction(obstacle_fun, (nx, ny, nz))
# 初始速度曲线:几乎为零,有一个轻微的扰动来触发不稳定。
def inivel(d, x, y, z):
return (1-d) * uLB * (1+1e-4*sin(y/ly*2*pi))
vel = fromfunction(inivel, (3, nx, ny, nz))
# 以给定的速度初始化处于平衡状态的种群
fin = equilibrium(1, vel)
f = open('xyz_'+str(Re)+'.dump', 'w')
f.close()
for time in tqdm(range(maxIter)):
# 右边界分布函数
fin[col3, -1, :, :] = fin[col3, -2, :, :]
#计算宏观密度和速度
rho, u = macroscopic(fin)
# 重新计算左边界的分布函数
u[:, 0, :, :] = vel[:, 0, :, :]
rho[0,:,:] = 1/(1-u[0,0,:,:]) * (sum(fin[col2,0,:,:], axis=0) + 2*sum(fin[col3,0,:,:], axis=0))
# 计算平衡态
feq = equilibrium(rho, u)
fin[[0,1,2,3,4],0,:,:] = feq[[18,17,16,15,14],0,:,:]+fin[[18,17,16,15,14],0,:,:]-feq[[18,17,16,15,14],0,:,:]
# 碰撞过程
fout = fin - omega * (fin - feq)
# 对圆柱内节点进行反弹
for i in range(19):
fout[i, obstacle] = fin[18-i, obstacle]
# 扩散过程
for i in range(19):
fin[i, :, :, :] = roll(roll(roll(fout[i,:,:],v[i,0], axis=0), v[i,1], axis=1), v[i,2], axis=2)
u_ = sqrt(u[0]**2+u[1]**2+u[2]**2)
# print(u_.shape)
# 写入数据
if (time%100==0):
f = open('xyz_'+str(Re)+'.dump', 'a')
line1 = "ITEM: TIMESTEP\n"
line2 = str(time) + "\n"
line3 = "ITEM: NUMBER OF ATOMS\n"
line4 = str(nx*ny*nz) + "\n"
line5 = "ITEM: BOX BOUNDS pp pp pp\n"
line6 = "0 " + str(nx) + "\n"
line7 = "0 " + str(ny) + "\n"
line8 = "0 " + str(nz) + "\n"
line9 = "ITEM: ATOMS id q x y z\n"
f.write(line1)
f.write(line2)
f.write(line3)
f.write(line4)
f.write(line5)
f.write(line6)
f.write(line7)
f.write(line8)
f.write(line9)
index = 1
for ix in range(nx):
for iy in range(ny):
for iz in range(nz):
f.write(str(index)+' '+str(u_[ix,iy,iz])+' '+str(ix)+' '+str(iy)+' '+str(iz)+'\n')
index += 1
f.close()