2021年数学建模国赛C题问题四及模型检验

2021年数学建模国赛C题问题四详细思路和代码

小编本次建模虽然没能获得国奖，但是还是想把思路分享给大家，希望大家多多批评与指正

1 问题分析

问题四要求确定企业每周产能可以提高多少，从题意来看，企业每周的产能是描述其生产能力和实力的指标，应当是企业长期的体现。并且题目中明确给出了企业当前情况下每周的产能为2.82万立方米，故我们认为：企业每周的产能应当是一个固定值，体现其本身的生产能力和综合情况。

确定概念后，我们对问题进行了分析，发现题目中实际上是要求我们对未来24周企业每周的产能进行优化，在相应的订购方案和转运方案下，达到尽量提高的目的。确定优化任务后，我们需要对优化目标进行量化。

结合前几个问题的分析，我们发现优化出来的订购方案和转运方案其实每周都可以满足企业当前的产能（2.82万立方米），为了找到企业到底能提高多少，我们对某一个订购方案和转运方案进行了分析，发现每周原材料都有剩余，数量各不相同。库存原料主要是为了防止未来某一周原料不够时出现停产情况，但是目前的情况是：每一周都有剩余，所以不会出现停产情况。那么，如果我们记录下24周中最小的库存量，然后在此基础上，每周均多用最小库存量的原料，这样该企业在每周的产能就得到了提高，且不会出现停线情况。

在这里插入图片描述
分析后，我们又发现只要找到不同方案下最小库存量的最大值，即可达到最大化提高企业每周产能的目的。而这个目的，完全可通过模拟退火算法得到，以最小库存量为优化目标，通过产生不同的订购和转运方案，优化最小库存量，使其最大化。问题三的具体思路如图8.1所示。

2 产能模型与方案产生

为了能优化企业每周的产能，我们给定的订购方案和转运方案下，通过每周原料的库存量构建了产能目标函数，下面给出第周库存产能的计算方法：
在这里插入图片描述
关于订购方案，首先我们基于402家供应商后24周的订货数据，结合AdaBoost算法对未来24周的订购量进行了预测，然后采用与问题三中公式(7-3)一致的初始化条件，但是不再采用优先级初始化方法，随机对订货数据进行初始化，得到订购方案。

关于转运方案，也需要基于已经初始化得订购方案进行初始化，其初始化方法和满足的条件与问题二一致，我们可参考公式(6-8)给出，这里不再赘述。

下面给出本问题优化的目标函数和相关限制条件：
在这里插入图片描述

3 优化结果

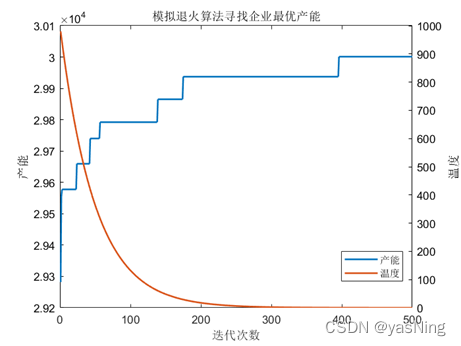
在实际优化过程中，我们选取外循环500次，内循环100次，初始温度给定为1000，温度衰减系数为0.98。最后通过模拟退火算法，优化出企业的最优产能为3万立方米左右，比起原产能2.82万立方米提高了6.4%左右。
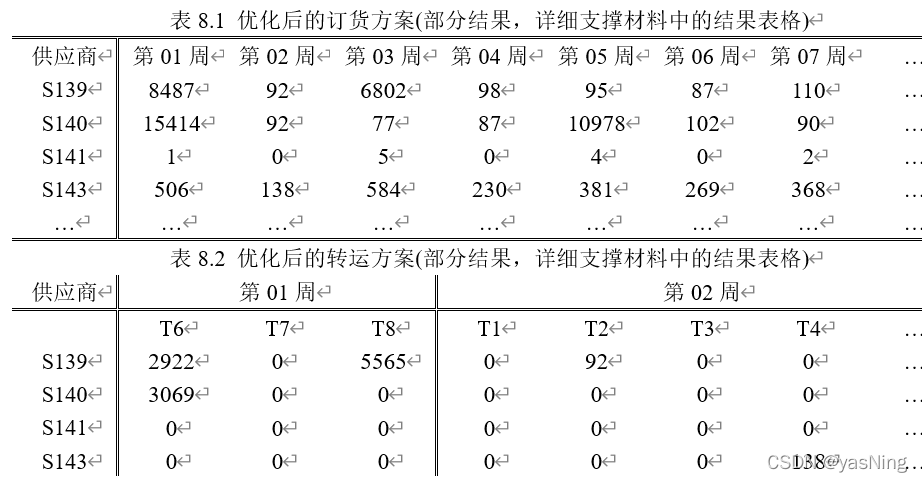
在这里插入图片描述
对应的订购方案和转运方案如下表所示：

模型的评估与检验

本文主要建立了经济效益模型与损耗模型，借助模拟退火算法对建立的模型进行了优化，给出了对应的订购和转运方案。

模型优点

（1）引入了随机森林算法构建经济效益模型，用随机森林算法训练时，各属性节点的权重量化解决了时间序列对经济效益的影响，同时利用了模型的预测概率量化了供应商的供货能力，一举两得。
（2）通过分析发现了数据呈周期性变化的特点，并以最后14周的数据为支撑，引入AdaBoost集成学习算法，对未来24周的订货量、供货量和损耗率进行了预测，模型回归系数高，可信性高。
（3）借助AdaBoost算法预测的未来24周的损耗率数据，构建了损耗模型；
（4）对于问题三中的双目标优化问题，提出“线性加权”的思路，实现优化问题的简化；
（5）引入灰度关联分析算法验证了供应商重要性模型的正确性；

模型缺点

随机森林模型、AdaBoost均是以预测为主，预测结果虽然精度高，但实际产生的意义难以准确说明，“黑盒性”比较大。

模型的检验

本部分旨在说明经济效益模型算法和AdaBoost算法选择的合理性：

（1）随机森林经济效益模型

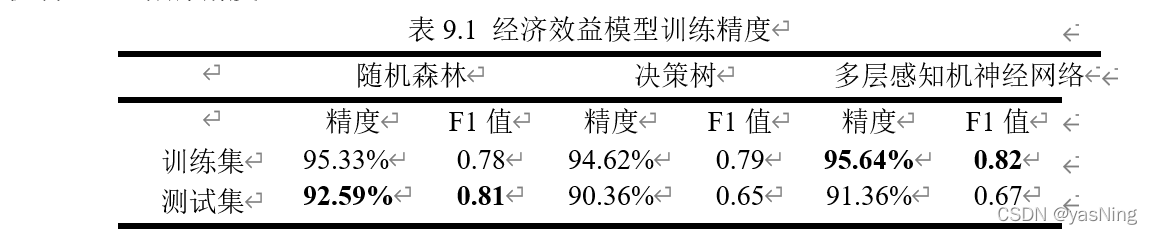
为了衡量时间序列对经济效益的影响，我们考虑使用决策树类或者神经网络类算法，能够在训练结束后返回属性节点（即训练集中各维度）的重要性，得到时间序列权重。下表反映了在训练集：测试集为“8：2”的情况下，利用随机森林、决策树和多层感知机神经网络的精度：
在这里插入图片描述
比起其他两种算法随机森林算法用于经济效益模型训练时，随机森林在测试时能达到更高的精度和更高的F1值，故选择了随机森林算法具有合理性。

（2）AdaBoost集成学习回归模型

在前期算法选择上，我们尝试了常见的用于回归的算法：岭回归、支持向量机、Logistic回归，但是拟合效果均很差，所以尝试使用集成学习的强学习算法AdaBoost进行回归预测，上述算法的回归系数如下表：
在这里插入图片描述
从回归系数来看，AdaBoost在性能上远超其他常用的拟合预测算法，这是也是集成学习器是强学习器的体现。故我们选择AdaBoost算法用于拟合预测未来24周订货量、供货量和损耗率。

模型的推广

对于国内生产企业原材料的订购和转运场景，可以将本文所建立的模型经过一定的改进与优化，用到实际生产中。可为企业定制订购和转运方案，将算法模型写入企业管理系统中，实际嵌入到企业的管理平台中，对原材料的订购和转运问题进行实时管控，进而达到助工助产的目的。

随机初始化转运方案代码

% 随机初始化转运方案
function [trans_plan] = Init_trans(order_plan, waste)
trans_plan = zeros(402, 8 * 24);
for i = 1:24
    waste_week = waste(:, i);
    ranp = zeros(8, 1);
    transporter = [];
    for t = 1:8
        if waste_week(t) ~= 0
            transporter = [transporter, t];
        end
    end
    
    for j = 1:402
        if order_plan(j, i) ~= 0
            rand_num = transporter(randperm(numel(transporter), 1)); 
            if ranp(rand_num) + order_plan(j, i) < 6000
                ranp(rand_num) = ranp(rand_num) + order_plan(j, i);
                trans_plan(j, (i - 1) * 8 + rand_num) = order_plan(j, i);
            else
                surplus = ranp(rand_num) + order_plan(j, i) - 6000;
                ranp(rand_num) = 6000;
                trans_plan(j, (i - 1) * 8 + rand_num) = order_plan(j, i) - surplus;
                
                rand_num = transporter(randperm(numel(transporter), 1));
                while ranp(rand_num) + surplus > 6000
                    if ranp(rand_num) < 6000
                        surplus = surplus - (6000 - ranp(rand_num));
                        trans_plan(j, (i - 1) * 8 + rand_num) = (6000 - ranp(rand_num));
                        ranp(rand_num) = 6000;
                    end
                    rand_num = transporter(randperm(numel(transporter), 1)); 
                end
                ranp(rand_num) = ranp(rand_num) + surplus;
                trans_plan(j, (i - 1) * 8 + rand_num) = surplus;
            end
        end
    end
end
end

退火代码

load('..\predict_402.mat');
load('..\predict_waste.mat');
load('..\prob.mat');
class = prob(:, 3);

%% 模拟退火算法寻找产能最大
T0 = 1000;
T = T0;
maxOutTimes = 500;  % 外循环
maxInTimes = 100;  % 内循环
alfa = 0.98; 
%随机产生初始解
[x10, x20, capacity0] = t4_init(predict_402, predict_waste, class);
y0 = min(capacity0);

%% 定义一些保存中间过程的量
max_y = y0;   
MAXY = zeros(maxOutTimes, 1);
temp = zeros(maxOutTimes, 1);

%% 模拟退火过程
% 外循环
for iter = 1 : maxOutTimes  
    % 内循环
    for i = 1 : maxInTimes 
        %% 随机产生新解
        [x1, x2, capacity] = t4_init(predict_402, predict_waste, class);
        
        %% 记录新解，并计算新解的函数值，保存最优解
        y1 = min(capacity);
        % 如果新解函数值大于当前解的函数值
        if y1 > y0    
            % 更新当前解为新解
            x10 = x1; 
            x20 = x2;
            y0 = y1;
            capacity0 = capacity;
            
        %%根据Metropolis准则计算一个概率
        else
            p = exp(-(y0 - y1) / T); 
            if rand(1) < p
                % 更新当前解为新解
                x10 = x1; 
                x20 = x2;
                y0 = y1;
                capacity0 = capacity;
            end
        end
        
        % 判断是否要更新找到的最佳的解
        if y0 > max_y  
            max_y = y0;  
            best_x1 = x10; 
            best_x2 = x20; 
            best_c = capacity;
        end
    end
    
    % 记录本次外循环结束后找到的最优解
    MAXY(iter) = max_y; 
    T = alfa * T; 
    temp(iter) = T;
end

disp('该企业每周的产能为：'); 
disp(max_y);
xlswrite('..\附件A 订购方案数据结果.xlsx', best_x1, '问题4的订购方案结果', 'B7:Y408');
xlswrite('..\附件B 转运方案数据结果.xlsx', best_x2, '问题4的转运方案结果', 'B7:GK408');

%% 画出每次迭代后找到的最小值的图形
fig = figure;
X = 1:maxOutTimes;
yyaxis left
plot(X, MAXY);
ylabel('产能');
yyaxis right
plot(X, temp);
ylabel('温度');
xlabel('迭代次数');
title('模拟退火算法寻找企业最优产能');
legend('产能', '温度');