1. 基本概念

模拟鸟类觅食行为

个体最优：每一只鸟飞过的最优解

全局最优：全部鸟飞过的最优解

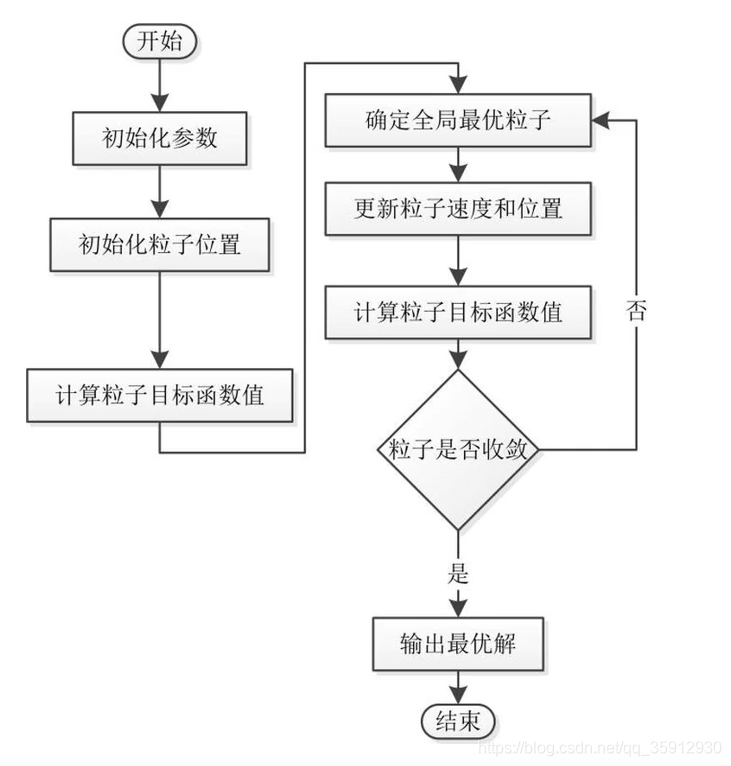
2. 算法流程图

3. 迭代方程

$$V_i^{t+1}=\omega V_i^t+c_1{r}_1(P_{ibest}^t-X_i^t)+c_2{r}_2(G_{best}^t-X_i^t)$$

• $\omega V_i^t$：惯性
• $c_1{r}_1(P_{ibest}^t-X_i^t)$：个体最优
• $c_2{r}_2(G_{best}^t-X_i^t)$：全局最优

$$X_i^{t+1}=X_i^t+V_i^{t+1}$$

• $X_i^{t+1}$：下一时刻位置
• $X_i^t$：当前位置
• $V_i^{t+1}$：下一时刻速度

图示

4. 代码示例

%目标函数
%能找目标函数的最小值
%如果找最大值，前加负号
function y = fun(x)
y = sum(x.^2);

clc
clear

c1 = 1.5;
c2 = 1.5;
w=1;

gen = 200;      %迭代次数
size_pop = 50;   %种群大小

pop_max = 100;  %搜索范围
pop_min = -100;  

nVar = 2;
V_max = 5;   %速度最值
V_min = -5;   %不能跨度太大，搜索精度不够，跨度太小，迭代次数过大


%初始种群
for i = 1 : size_pop
    pop(i,:) = (pop_max - pop_min) * rands(1,nVar) ;  %初始种群的位置
    V(i,:) = (V_max - V_min) * rands(1,nVar);   %初始种群的速度
    fitness(i) = fun(pop(i,:)); %初始种群的目标函数
end

%初始化
[best_fitness,best_index] = max(fitness);   %
g_best = pop(best_index,:);
p_best = pop;

fitness_p_best = fitness;   %个人最优解
fitness_g_best = best_fitness;  %全局最优解



for i = 1:gen
    for j = 1:size_pop
        %更新速度
        V( j,: ) = V(j,:) + c1 * rand *(p_best(j,:) - pop(j,:)) + c2 * rand* (g_best(1,:) - pop(j,:));
        V( j, find(V(j,:) > V_max )) = V_max;
        V( j ,find(V(j,:) < V_min )) = V_min;
        
        %更新位置
        pop(j,:) = pop(j,:) + V(j,:);
        pop( j, find(pop(j,:) > pop_max )) = pop_max;
        pop( j ,find(pop(j,:) < pop_min )) = pop_min;
   
        %
        fitness(j) = fun(pop(j,:));
    end
    
    
    for j = 1:size_pop
        %更新个人最优
        if fitness(j) < fitness_p_best(j)
            p_best(j,:) = pop(j,:);
            fitness_p_best(j) = fitness(j);
        end
        
        %更新全局最优
        if fitness(j) < fitness_g_best
            g_best = pop(j,:);
            fitness_g_best = fitness(j)
        end
    end
    yy(i) = fitness_g_best;
end

plot(yy)
title('最优个体适应度','fontsize',12);
xlabel('迭代次数','fontsize',12);
ylabel('适应度','fontsize',12);

disp('函数值         变量')
disp([fitness_g_best,g_best]);

5. 特点

(1) 优点

1. 理解简单

(2) 缺点

1. 如果初始点选择不均匀，易出现收敛到局部最优解。

2. 无法处理约束条件

6. 改良

(1) 惩罚函数

将有约束的目标函数转换为无约束的目标函数

降低分值，使其淘汰

%增加约束条件后的目标函数
function y = fun(x)
y = sum(x.^2);

if x(1) + x(2) > 2	%满足约束的正常
	y=y;
else		%不满足约束的淘汰
	y = y + 1000;
end

(2) 增加变异操作

避免陷入局部最优解