0 前言

本文是研究飞控过程中的学习笔记，系统分析了四旋翼飞行器的坐标变换、运动学与动力学模型，以此作为飞控开发的基础。

1 无人机的坐标变换

1.1 坐标系¹

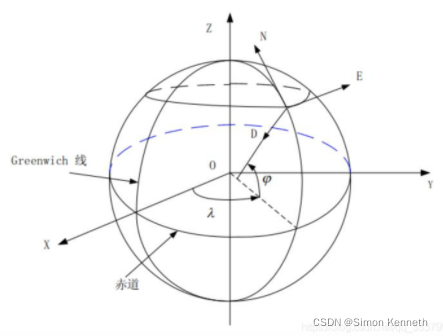
1.1.1 地心坐标系

地球中心坐标系，即坐标系原点位于地心。X轴通过格林尼治线和赤道线的交点，正方向为原点指向交点方向。 Z轴通过原点指向北极。 Y轴与X，Z轴构成右手坐标系。

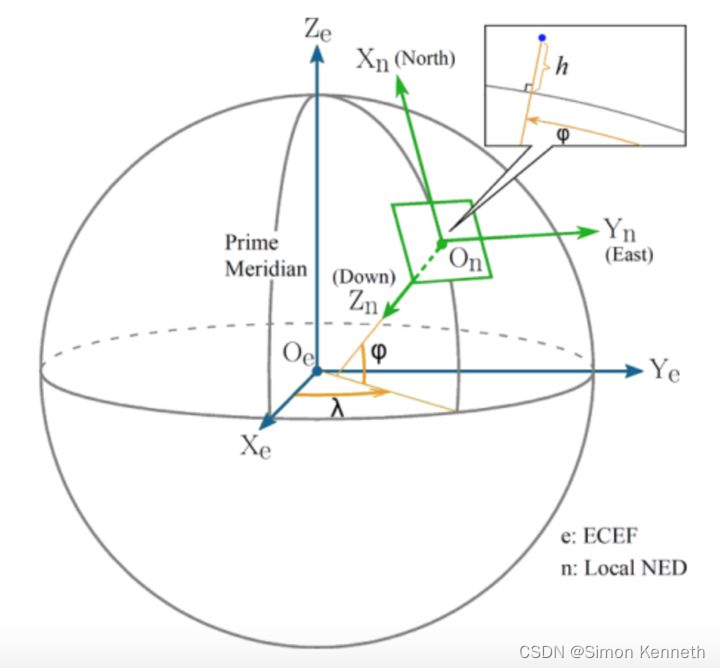
1.1.2 NED（北东地）坐标系

由于地心坐标系建立产生的GPS信号是以前面的形式存在，而现实无人机控制中需要在平面，因此引入了NED坐标系，如图绿色部分即为NED坐标系。NED坐标系是在导航计算时使用的坐标系。向量分别指向北，东，地，因此NED坐标系也经常称为北东地坐标系。

通常我们以NED为确定无人机位姿的参考坐标系，因此当无人机向上飞时，NED坐标系下的z坐标实际上是减小的。

1.1.3 机体坐标系

机体坐标系与机体固联，随飞机一起相对地球运动。x轴沿机头正方向，y轴沿机身右侧，z轴由右手定则得到。

1.2 旋转矩阵

与机器人学的内容相似，这里只放结果：
$$\begin{gathered} R_x(\theta )=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \theta & \sin \theta \\ 0& -\sin \theta & \cos \theta \end{array}\right] \\ {R}_y(\theta )=\left[\begin{array}{ccc}\cos \theta & 0& -\sin \theta \\ 0& 1& 0\\ \sin \theta & 0& \cos \theta \end{array}\right] \\ {R}_z(\theta )=\left[\begin{array}{ccc}\cos \theta & \sin \theta & 0\\ -\sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]\text{\hspace{1em}(1-1)} \end{gathered}$$

分别表示绕基坐标系$x,y,z$轴旋转$\theta$后的旋转矩阵。
$$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=R(\theta )\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\end{array}\right]\text{\hspace{1em}(1-2)}$$
我们用一个通用的旋转矩阵来表示从机体坐标系$O_b{x}_b{y}_b{z}_b$到地球坐标系$O_e{x}_e{y}_e{z}_e$的旋转矩阵，滚转角：绕x轴转$\varphi$；俯仰角：绕y轴转$\theta$；偏航角：绕z轴转$\psi$，则有
$$\begin{array}{rl}{R}_b^e(\varphi ,\theta ,\psi )& =R(\varphi )R(\theta )R(\psi )\\ & =\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \varphi & \sin \varphi \\ 0& -\sin \varphi & \cos \varphi \end{array}\right]\left[\begin{array}{ccc}\cos \theta & 0& -\sin \theta \\ 0& 1& 0\\ \sin \theta & 0& \cos \theta \end{array}\right]\left[\begin{array}{ccc}\cos \psi & \sin \psi & 0\\ -\sin \psi & \cos \psi & 0\\ 0& 0& 1\end{array}\right]\\ & =\left[\begin{array}{ccc}\cos \theta \cos \psi & \cos \psi \sin \theta \sin \varphi -\sin \psi \cos \varphi & \cos \psi \sin \theta \cos \varphi +\sin \psi \sin \varphi \\ \cos \theta \sin \psi & \sin \psi \sin \theta \sin \varphi +\cos \psi \cos \varphi & \sin \psi \sin \theta \cos \varphi -\cos \psi \sin \varphi \\ -\sin \theta & \sin \varphi \cos \theta & \cos \varphi \cos \theta \end{array}\right]\end{array}\text{\hspace{1em}(1-3)}$$

$$\left[\begin{array}{c}{x}_e\\ y_e\\ z_e\end{array}\right]=R(\varphi ,\theta ,\psi )\left[\begin{array}{c}{x}_b\\ y_b\\ z_b\end{array}\right]\text{\hspace{1em}(1-4)}$$

2 非线性动力学模型²

2.1 电机模型

电机旋翼产生的力与转速的平方成正比，单个旋翼的升力可以表示为：
$$F_i=c_T\cdot {\Omega }_i^2,i=(1,2,3,4)\text{\hspace{1em}(2-1)}$$
式中，$c_T$为电机拉力系数。则旋翼产生的总升力为
$$T=\sum _i^4{F}_i\text{\hspace{1em}(2-2)}$$
轴的陀螺力矩${\tau }_{gyo}=\omega \times J_r\Omega$，其中$J_r=\left[\begin{array}{ccc}{J}_{rx}& & \\ & J_{ry}& \\ & & J_{rz}\end{array}\right]$为电机的惯性矩阵。
$${\tau }_{gyo}=\left[\begin{array}{c}{\tau }_{gyo,\varphi }\\ {\tau }_{gyo,\theta }\\ {\tau }_{gyo,\psi }\end{array}\right]=\left[\begin{array}{c}{J}_{rx}({\Omega }_1-{\Omega }_2+{\Omega }_3-{\Omega }_4)q\\ J_{ry}(-{\Omega }_1+{\Omega }_2-{\Omega }_3+{\Omega }_4)p\\ 0\end{array}\right]\text{\hspace{1em}(2-3)}$$

当电机高速旋转的时候，相当于一个陀螺。高速旋转的陀螺是非常稳定的个体，具有保持自身轴向不变的能力。因此如果有外力想改变陀螺转轴的方向，那么会产生一个陀螺力矩来抵抗这种改变。

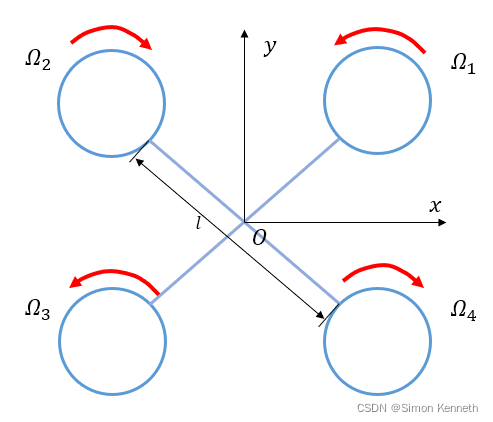
$\tau =[{\tau }_x{\tau }_y{\tau }_z{]}^T$为螺旋桨在机体轴上产生的力矩。以X型四旋翼为例，从右上角开始逆时针电机编号依次为1234，则
$$\tau =\left[\begin{array}{c}{\tau }_x\\ {\tau }_y\\ {\tau }_z\end{array}\right]=\left[\begin{array}{c}\frac{\sqrt{2}}{2}l{c}_M(-{\Omega }_1^2+{\Omega }_2^2+{\Omega }_3^2-{\Omega }_4^2)\\ \frac{\sqrt{2}}{2}l{c}_M({\Omega }_1^2+{\Omega }_2^2-{\Omega }_3^2-{\Omega }_4^2)\\ c_M({\Omega }_1^2-{\Omega }_2^2+{\Omega }_3^2-{\Omega }_4^2)\end{array}\right]\text{\hspace{1em}(2-4)}$$
式中，$l$为旋翼质心到整个四旋翼质心的距离，$c_M$为电机的力矩系数。

2.2 外力平衡方程(平动动力学)

质心运动方程为
$$\frac{\mathrm{d}(m\vec{V})}{\mathrm{d}t}=\vec{F}\text{\hspace{1em}(2-5)}$$
式中，$V=[v_x,v_y,v_z{]}^T$为无人机相对地面坐标系的速度向量，$\vec{F}$为作用在无人机上的合外力向量。

地面坐标系下四旋翼所受阻力为
$$\left[\begin{array}{c}{f}_x\\ f_y\\ f_z\end{array}\right]=\left[\begin{array}{c}{K}_1\dot{x}\\ K_2\dot{y}\\ K_3\dot{z}\end{array}\right]\text{\hspace{1em}(2-6)}$$
式中，$K_i$为空气阻力系数。则惯性坐标系下外力平衡方程为
$$m\left[\begin{array}{c}\ddot{x}\\ \ddot{y}\\ \ddot{z}\end{array}\right]=mg\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]-RT\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]-\left[\begin{array}{c}{K}_1\dot{x}\\ K_2\dot{y}\\ K_3\dot{z}\end{array}\right]\text{\hspace{1em}(2-7)}$$
进一步展开可得
$$\left[\begin{array}{c}\ddot{x}\\ \ddot{y}\\ \ddot{z}\end{array}\right]=\left[\begin{array}{c}-\frac{T}{m}(\cos \psi \sin \theta \cos \varphi +\sin \psi \sin \varphi )-K_1\dot{x}\\ -\frac{T}{m}(\sin \psi \sin \theta \cos \varphi -\cos \psi \sin \varphi )-K_2\dot{y}\\ g-\frac{T}{m}(\cos \varphi \cos \theta )-K_3\dot{z}\end{array}\right]\text{\hspace{1em}(2-8)}$$

2.3 外力矩平衡方程（转动动力学）

由欧拉方程可知，四旋翼绕质心的转动的动力学方程为
$$\begin{array}{rl}\vec{M}& =J\dot{\vec{\omega }}+\vec{\omega }\times J\vec{\omega }\\ & =\tau -{\tau }_{gyo}-{\tau }_f\end{array}\text{\hspace{1em}(2-9)}$$
式中$\omega =[p,q,r{]}^T$为飞行器相对机体坐标系的角速度向量，$J=\left[\begin{array}{ccc}{J}_x& & \\ & J_y& \\ & & J_z\end{array}\right]$为四旋翼无人机在机体坐标系三个轴上的转动惯量，由于我们假设四旋翼的重心正好位于几何中心，因此转动惯量$J_{xy}=J_{yx}=J_{xz}=J_{zx}=Jyz=J_{zy}=0$。$\vec{M}$为作用在飞行器上的合外力矩，${\tau }_f=K_f\omega$为空气阻力矩。
式（2-9a）展开后可得
$$\begin{array}{rl}\left[\begin{array}{c}{J}_x\dot{p}\\ J_y\dot{q}\\ J_z\dot{r}\end{array}\right]& =\left[\begin{array}{c}p\\ q\\ r\end{array}\right]\times \left[\begin{array}{c}{J}_{x}p\\ J_{y}q\\ J_{z}r\end{array}\right]\\ & =\left[\begin{array}{ccc}0& -r& q\\ r& 0& -p\\ -q& p& 0\end{array}\right]\times \left[\begin{array}{c}{J}_{x}p\\ J_{y}q\\ J_{z}r\end{array}\right]\\ & =\left[\begin{array}{c}qr(J_z-J_y)\\ pr(J_x-J_z)\\ pq(J_y-J_x)\end{array}\right]\end{array}\text{\hspace{1em}(2-10)}$$

联立（2-10）和（2-9b）可得
$$\left[\begin{array}{c}\dot{p}\\ \dot{q}\\ \dot{r}\end{array}\right]=\left[\begin{array}{c}\begin{array}{rl}& \frac{(J_y-J_z)}{J_x}qr+\frac{J_{rz}}{J_x}({\Omega }_1-{\Omega }_2+{\Omega }_3-{\Omega }_4)q+\frac{{\tau }_x}{J_x}-\frac{{\tau }_{fx}}{J_x}\\ & \frac{(J_z-J_x)}{J_y}pr+\frac{J_{rz}}{J_y}(-{\Omega }_1+{\Omega }_2-{\Omega }_3+{\Omega }_4)p+\frac{{\tau }_y}{J_y}-\frac{{\tau }_{fy}}{J_y}\\ & \frac{(J_x-J_y)}{J_z}pq+\frac{{\tau }_z}{J_z}-\frac{{\tau }_{fz}}{J_z}\end{array}\end{array}\right]\text{\hspace{1em}(2-11)}$$

• 机体坐标系下角速度和惯性坐标系下角速度的关系为³

$$\left[\begin{array}{c}\dot{\varphi }\\ \dot{\theta }\\ \dot{\psi }\end{array}\right]=\left[\begin{array}{ccc}1& \sin \varphi \tan \theta & \cos \varphi \tan \theta \\ 0& \cos \varphi & -\sin \varphi \\ 0& (\sin \varphi /\cos \theta )& (\cos \varphi /\cos \theta )\end{array}\right]\left[\begin{array}{c}p\\ q\\ r\end{array}\right]\text{\hspace{1em}(2-12)}$$

$$\left[\begin{array}{c}p\\ q\\ r\end{array}\right]=\left[\begin{array}{ccc}1& 0& -\sin \theta \\ 0& \cos \varphi & \cos \theta \sin \varphi \\ 0& -\sin \varphi & \cos \theta \cos \varphi \end{array}\right]\left[\begin{array}{c}\dot{\varphi }\\ \dot{\theta }\\ \dot{\psi }\end{array}\right]\text{\hspace{1em}(2-13)}$$

2.4 飞行控制刚体模型

联立（2-12）和（2-10），并考虑在机身稳定点处做线性化（$\theta \to 0$）可得
$$\left[\begin{array}{c}\ddot{\varphi }\\ \ddot{\theta }\\ \ddot{\psi }\end{array}\right]=\left[\begin{array}{c}\begin{array}{rl}& \frac{1}{J_x}[{\tau }_x+qr(J_x-J_z)-J_{xr}q{\Omega }_{gyo}-{\tau }_{fx}]\\ & \frac{1}{J_y}[{\tau }_y+pr(J_z-J_x)+J_{yr}q{\Omega }_{gyo}-{\tau }_{fy}]\\ & \frac{1}{J_z}[{\tau }_z+pq(J_x-J_y)\end{array}\end{array}\right]\text{\hspace{1em}(2-14)}$$

式中${\Omega }_{gyo}={\Omega }_1-{\Omega }_2+{\Omega }_3-{\Omega }_4$。

将式（2-8）和（2-14）写在一起，并令$[U_1{U}_2{U}_3{U}_4{]}^T=[T{\tau }_x{\tau }_y{\tau }_z]$⁴（动力学模型的输入量），可得
$$\left[\begin{array}{c}\ddot{x}\\ \ddot{y}\\ \ddot{z}\\ \ddot{\varphi }\\ \ddot{\theta }\\ \ddot{\psi }\end{array}\right]=\left[\begin{array}{c}\begin{array}{rl}& -\frac{T}{m}(\cos \psi \sin \theta \cos \varphi +\sin \psi \sin \varphi )-K_1\dot{x}\\ & -\frac{T}{m}(\sin \psi \sin \theta \cos \varphi -\cos \psi \sin \varphi )-K_2\dot{y}\\ & g-\frac{T}{m}(\cos \varphi \cos \theta )-K_3\dot{z}\\ & \frac{1}{J_x}[{\tau }_x+qr(J_x-J_z)-J_{xr}q{\Omega }_{gyo}-{\tau }_{fx}]\\ & \frac{1}{J_y}[{\tau }_y+pr(J_z-J_x)+J_{yr}q{\Omega }_{gyo}-{\tau }_{fy}]\\ & \frac{1}{J_z}[{\tau }_z+pq(J_x-J_y)\end{array}\end{array}\right]\text{\hspace{1em}(2-15)}$$
式（2-15）即为四旋翼飞行器的非线性六自由度模型。

参考文献