一、引言
最近在手写遗传算法,想尝试解决一些优化问题。然而,在编码的过程中,自己发现了很多都不懂的问题。比如,交叉的操作,有单点交叉、两点交叉和多点交叉,具体选哪一种会更好呢?未知。还有交叉的概率,以及变异的概率,取多少才算合理呢?未知。最后就是轮盘赌选择法,在实现的时候,也有一点小疑惑,就是:通过Python的random没办法直接使用choice、choices或sample进行选择。所以,只好通过手动的方式写一个了。
二、轮盘赌选择法/Roulette Wheel Selection Method
轮盘赌选择法,即Roulette Wheel Selection Method,又称为Fitness Proportionate Selection Method。常用于遗传算法染色体的选择。从选择的个数来看,如果只是一个,那么很好实现。但如果是从多个选择之中选择一个,那么就稍微复杂一些了。
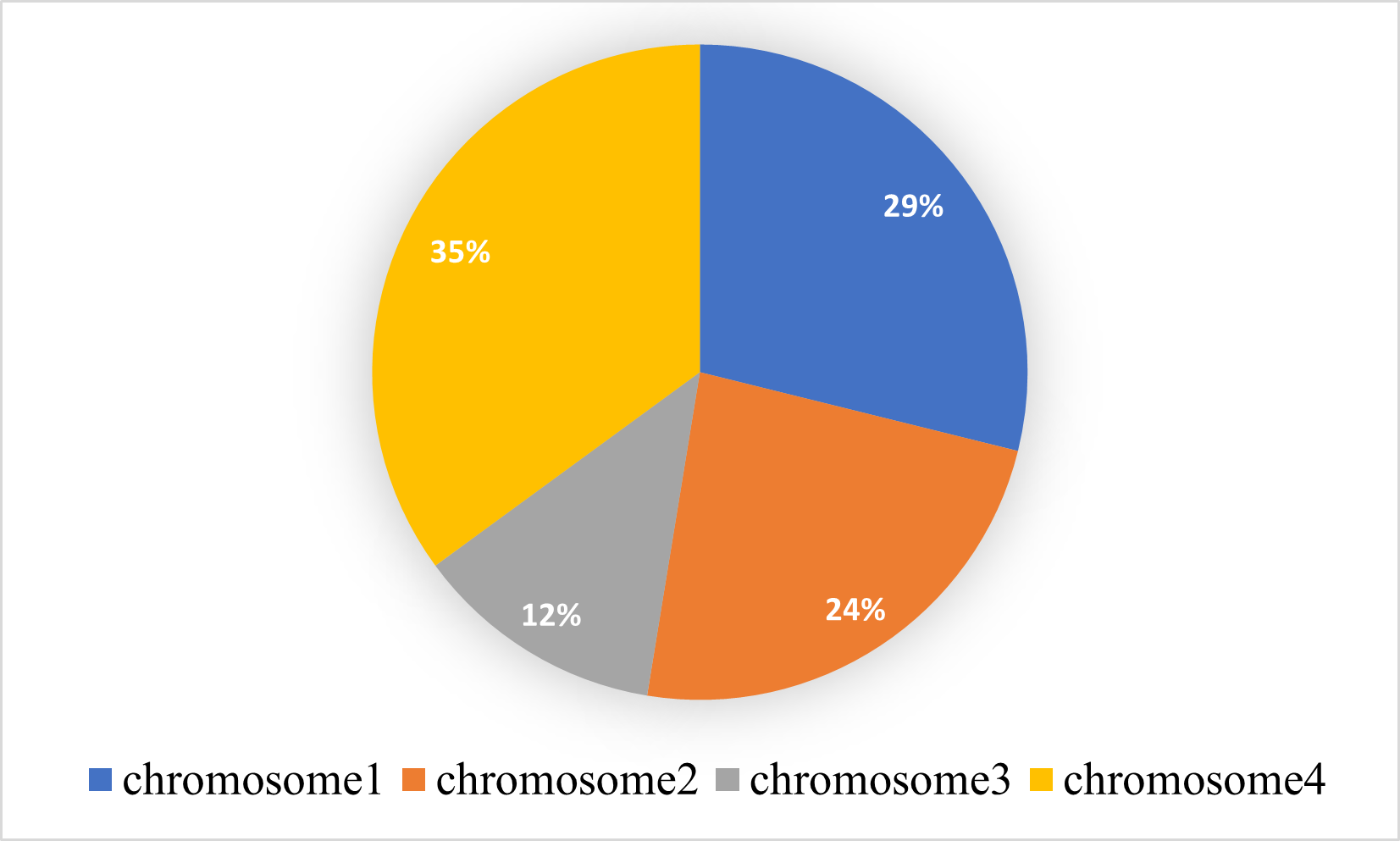
想象有一个轮盘,现在我们将它分割成m个部分,而这里的m代表我们总体中染色体的个数。每条染色体在轮盘上占有的区域面积将根据适应度分数成比例表达出来。例如m=4,而各条染色体的适应度分数分别为28、23、12、34。那么,轮盘的形状如下:
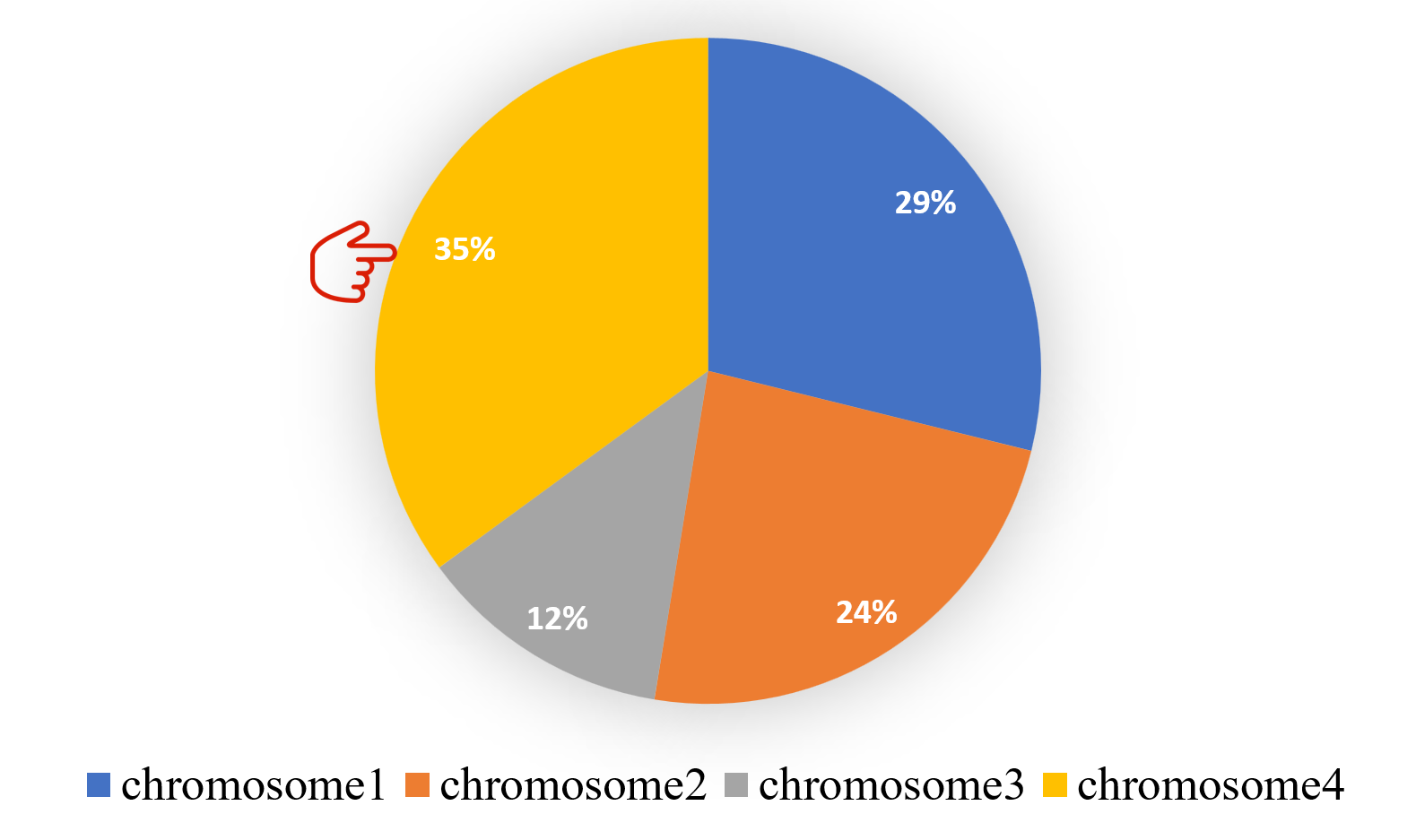
假设有一个固定的指针固定在圆盘周长上的某一点,轮盘开始旋转,那么当旋转停止时,就能够确定指针停留在哪个区域,并根据此区域能够选择出一个染色体。例如,
这样,第一个染色体便被选了出来,而且它被选中的概率是35%(34/(28+23+12+34))。此时如果要选出第二个染色体,就拥有两种实现方式了:
①轮盘中不删除chromosome4,如果通过旋转随机停下选出来的还是chromosome4,就重新选择,直到选出一个染色体不是chromosome4为止。
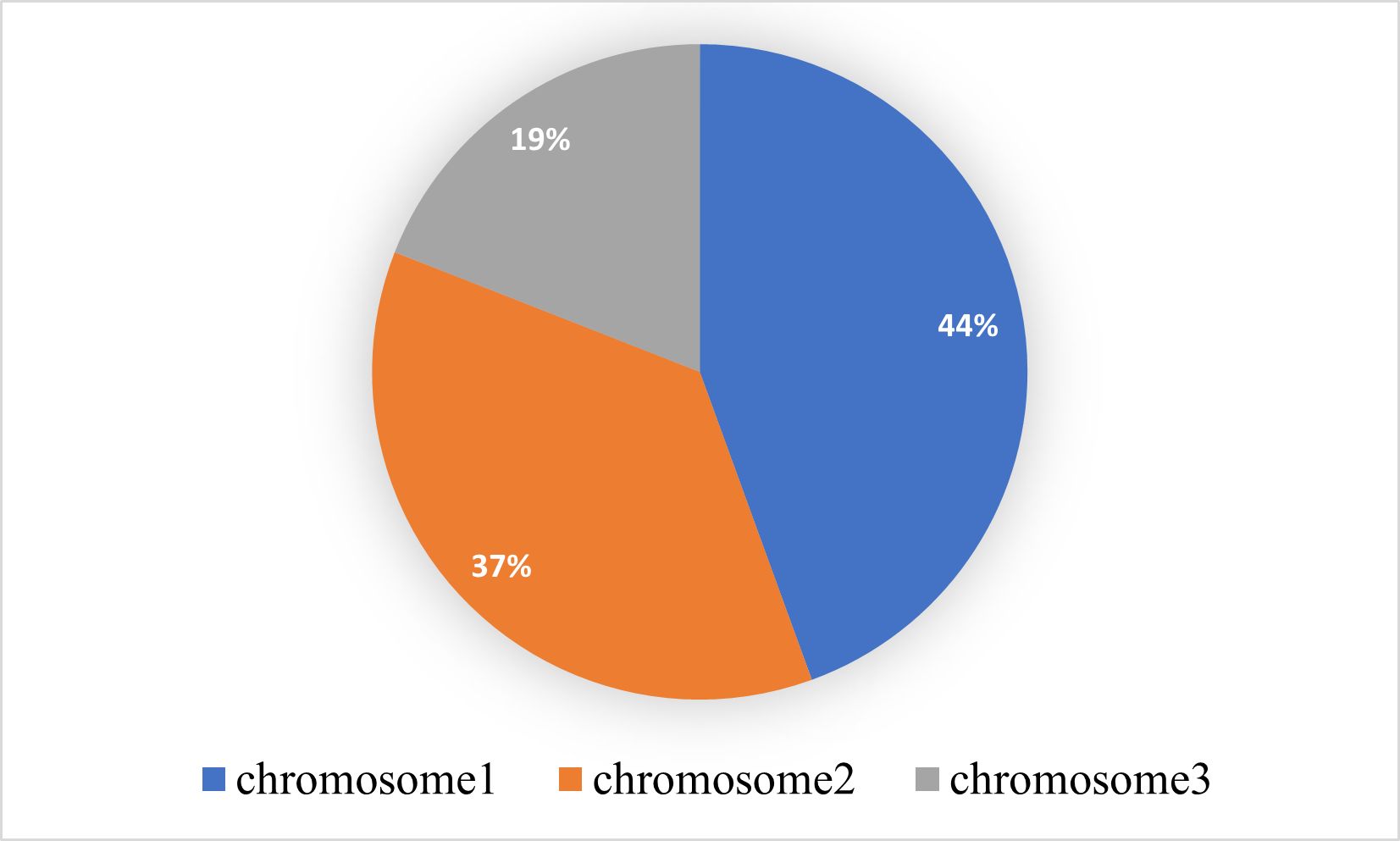
②轮盘中删除chromosome4,然后按照下面的轮盘进行选择:
显然,在第二种实现方法中,各染色体被选中的概率已经发生了变化。而且,第一种实现方法存在一个比较明显的缺点,就是:有可能一直都选择同一个染色体,尽管选择的尝试越久、概率越低,这导致选择的效率下降。第一种实现方式还有一个缺点是,选择到两个不同的染色体的概率是不可计算的,因为轮盘选择的结果拥有无数个(例如,每次旋转都被选中相同的chromosome4,导致一个死循环并不断做轮盘选择);而第二种的概率是可以被计算,因为每种选择的结果确定(例如,chromosome4-chromosome1、chromosome4-chromosome2或chromosome4-chromosome3)。
因此,这里推荐使用第二种实现方式实现轮盘赌选择法。
三、基于Python的实现方式
编程思想很简单,大概如下。生成一个[0,total_fitness)的随机数R:
如果R≤28,则选择chromosome1;
如果28<R≤28+23,则选择chromosome2;
如果28+23<R≤28+23+12,则选择chromosome3;
如果28+23+12<R≤28+23+12+34,则选择chromosome4。
当需要选择第二个染色体时,就从list中进行删除,当然fitness所对应的list也需要进行删除。
实现方式为:
import copy
import random
# function: achieve the roulette wheel selection method
# population_list: the list of optional chromosomes
# fitness_list: the corresponding fitness of chromosomes
# num_selection: the number of chromosome selection
def rw_selection(chromosome_list, fitness_list, num_selection):
# copy a duplicate of the population
cp_chromosome_list = copy.deepcopy(chromosome_list)
cp_fitness_list = copy.deepcopy(fitness_list)
# define a list for save the selected chromosomes
selected_chromosome_list = []
# select m chromosomes from cp_chromosome_list
for _ in range(num_selection):
# calculate the current sum of chromosome fitness
total_fitness = sum(cp_fitness_list)
# judge which chromosome is selected
random_value = random.uniform(0, total_fitness)
cumulative_fitness = 0
for i, chromosome in enumerate(cp_chromosome_list):
cumulative_fitness += cp_fitness_list[i]
if cumulative_fitness >= random_value:
# select a chromosome
selected_chromosome_list.append(chromosome)
# remove the corresponding chromosome and fitness
cp_chromosome_list.pop(i)
cp_fitness_list.pop(i)
break
# return the selection result
return selected_chromosome_list
# enter of the program
if __name__ == '__main__':
p = ['chromosome1', 'chromosome2', 'chromosome3', 'chromosome4']
f = [28, 23, 12, 34]
m = 2
for _ in range(10):
selected_p = rw_selection(p, f, m)
print(selected_p)四、运行结果和讨论
['chromosome3', 'chromosome4']
['chromosome1', 'chromosome2']
['chromosome2', 'chromosome1']
['chromosome3', 'chromosome1']
['chromosome1', 'chromosome2']
['chromosome1', 'chromosome3']
['chromosome4', 'chromosome1']
['chromosome4', 'chromosome2']
['chromosome3', 'chromosome4']
['chromosome4', 'chromosome1']Process finished with exit code 0
从运行的结果来看,chromosome4和chromosome1被优先选择的概率较高,因为chromosome4被选择的次数为5/20,而chromosome1被选择的次数为7/20。另外,chromosome2被选择的次数为4/20,chromosome3被选择的次数为4/20。基本上符合fitness的分布,但由于试验次数太少,chromosome4被选择的次数要少于chromosome1。
五、总结
其实感觉这篇博客的意义不是很大,但是怕自己以后还遇到这个小问题,所以,还是记录一下比较好。如果博客中出现一些问题,还请广大网友批评指正。
六、参考资料
1. 遗传算法