前言

本题由于没有合适答案为以往遗留问题，最近有时间将以往遗留问题一一完善。

142. 环形链表 II

不积跬步，无以至千里；不积小流，无以成江海，Swift社区 伴你前行。如果大家有建议和意见欢迎在文末留言，我们会尽力满足大家的需求。

难度水平：中等

摘要

链表问题中，查找环的起始节点是一个经典的进阶题目。本篇文章将讲解如何在 Swift 中实现 查找链表入环点 的算法，并通过 快慢指针法 实现 O(1) 空间复杂度，详细分析代码逻辑并给出完整的测试案例。

描述

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

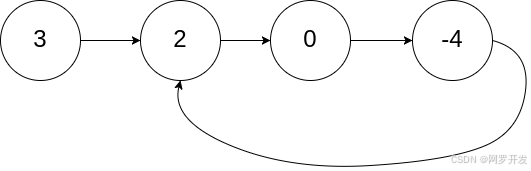
输入： head = [3,2,0,-4], pos = 1
输出： 返回索引为 1 的链表节点
解释： 链表中有一个环，其尾部连接到第二个节点。

示例 2：

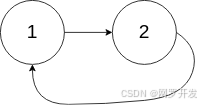
输入： head = [1,2], pos = 0
输出： 返回索引为 0 的链表节点
解释： 链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入： head = [1], pos = -1
输出： 返回 null
解释： 链表中没有环。

提示：

• 链表中节点的数目范围在范围 [0, 104] 内
• -105 <= Node.val <= 105
• pos 的值为 -1 或者链表中的一个有效索引

进阶： 你是否可以使用 O(1) 空间解决此题？

题解答案

我们采用 快慢指针法 解决该问题。
在之前判断链表是否存在环的基础上，进一步确定环的起始节点。

核心思路：

1. 使用快慢指针判断链表是否有环。
2. 若有环，快慢指针相遇时，将其中一个指针重新指向链表头节点，并保持另一个指针在相遇点。
3. 两个指针以相同的速度前进，相遇时的节点即为入环点。

题解代码

以下是 Swift 实现代码：

// 定义链表节点
class ListNode {
    var val: Int
    var next: ListNode?
    
    init(_ val: Int) {
        self.val = val
        self.next = nil
    }
}

func detectCycle(_ head: ListNode?) -> ListNode? {
    var slow = head
    var fast = head
    
    // 快慢指针判断是否有环
    while let nextFast = fast?.next {
        slow = slow?.next
        fast = nextFast.next
        if slow === fast {
            // 有环，查找环的起点
            var pointer1 = head
            var pointer2 = slow
            while pointer1 !== pointer2 {
                pointer1 = pointer1?.next
                pointer2 = pointer2?.next
            }
            return pointer1
        }
    }
    // 无环
    return nil
}

题解代码分析

1. 快慢指针的初始化

   • 慢指针每次走一步，快指针每次走两步。
   • 快指针达到链表末尾时（fast == nil 或 fast.next == nil），说明链表无环。

2. 检测环的存在

   • 若快慢指针在某个节点相遇，则链表中存在环。
   • 慢指针和快指针的路径会在环中循环，从而必定相遇。

3. 确定环的起始节点

   • 相遇后，将其中一个指针（如 pointer1）重新指向链表头节点，另一个指针（如 pointer2）保持在相遇点。
   • 两个指针每次走一步，最终相遇时的节点即为环的起始节点。

4. 时间复杂度

   • 检测环的阶段：O(n)，链表节点最多被访问两次。
   • 找入环点的阶段：O(n)，快慢指针最多走一圈。
   • 总时间复杂度：O(n)。

5. 空间复杂度

   • 只使用了两个指针，空间复杂度为 O(1)。

示例测试及结果

以下是测试代码：

// 创建测试用例
func createLinkedListWithCycle(_ values: [Int], _ pos: Int) -> ListNode? {
    guard !values.isEmpty else { return nil }
    let head = ListNode(values[0])
    var current = head
    var cycleNode: ListNode? = nil
    
    for i in 1..<values.count {
        let node = ListNode(values[i])
        current.next = node
        current = node
        if i == pos {
            cycleNode = node
        }
    }
    
    // 创建环
    if let cycleNode = cycleNode {
        current.next = cycleNode
    }
    
    return head
}

// 示例 1
let head1 = createLinkedListWithCycle([3, 2, 0, -4], 1)
print(detectCycle(head1)?.val ?? "No cycle") // 输出: 2

// 示例 2
let head2 = createLinkedListWithCycle([1, 2], 0)
print(detectCycle(head2)?.val ?? "No cycle") // 输出: 1

// 示例 3
let head3 = createLinkedListWithCycle([1], -1)
print(detectCycle(head3)?.val ?? "No cycle") // 输出: No cycle

测试结果:

2
1
No cycle

时间复杂度

• 检测环的复杂度：每个节点最多访问两次，复杂度为 O(n)。
• 找入环点的复杂度：环内最多走一圈，复杂度为 O(n)。
• 总复杂度：O(n)。

空间复杂度

• 仅使用两个指针变量，额外空间为常量 O(1)。

总结

本题通过 快慢指针法 高效解决了链表入环点的查找问题。在实际开发中，这种方法不仅可以用于链表问题，还可扩展到许多类似的循环检测场景。

关键点总结：

• 快慢指针的技巧。
• 环形结构的性质。
• 利用数学和逻辑简化复杂问题。

本篇文章中提供的代码实现和详细解释，希望能帮助您掌握链表环问题的核心解法。如果有疑问或更好的优化建议，欢迎讨论！