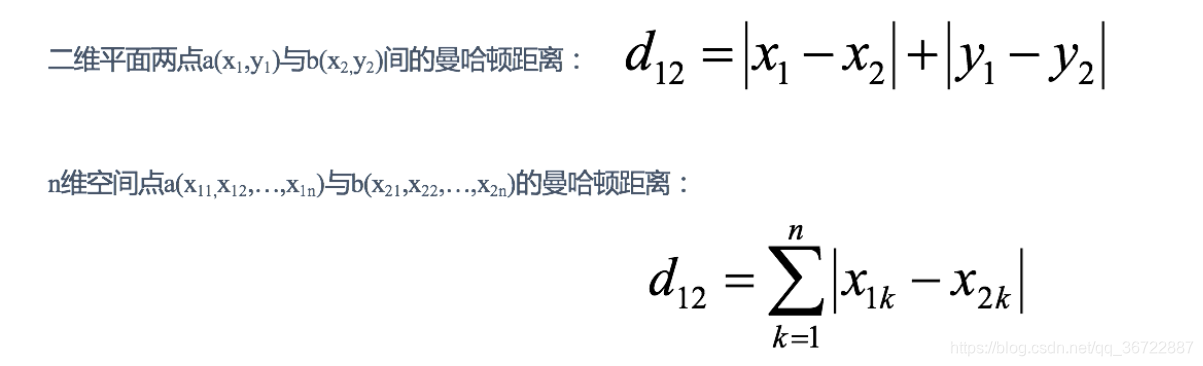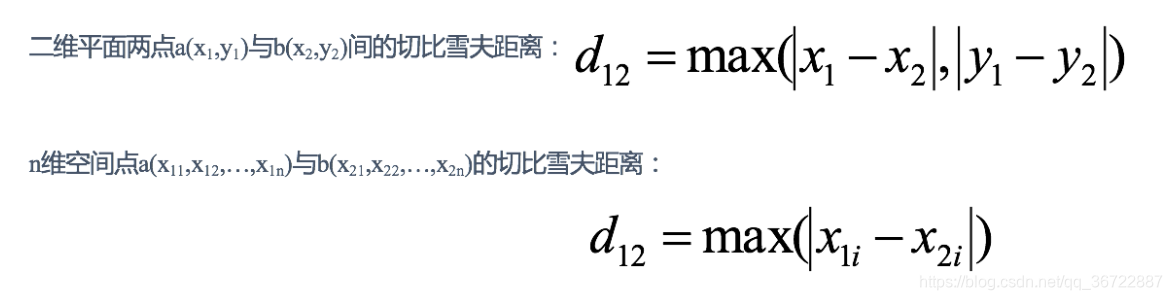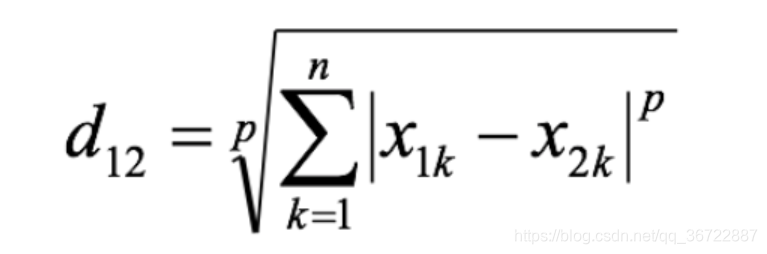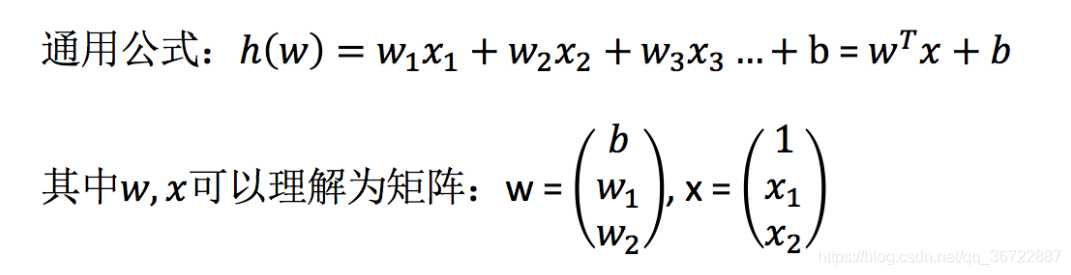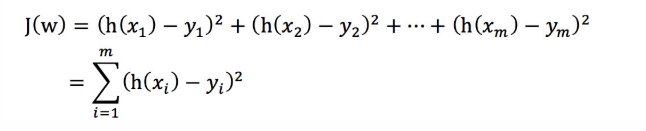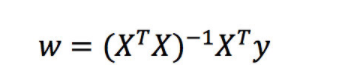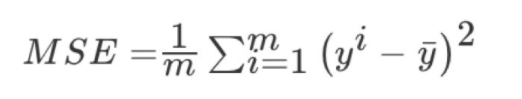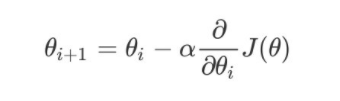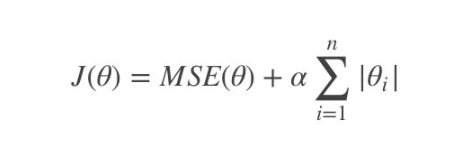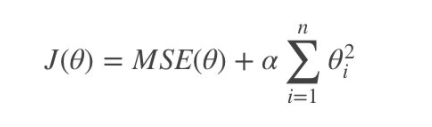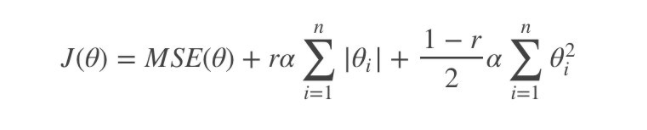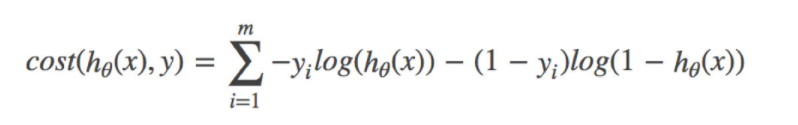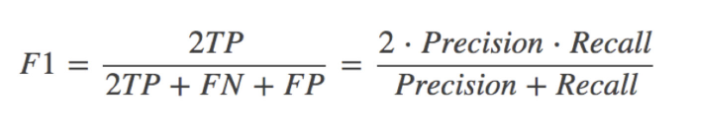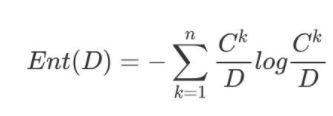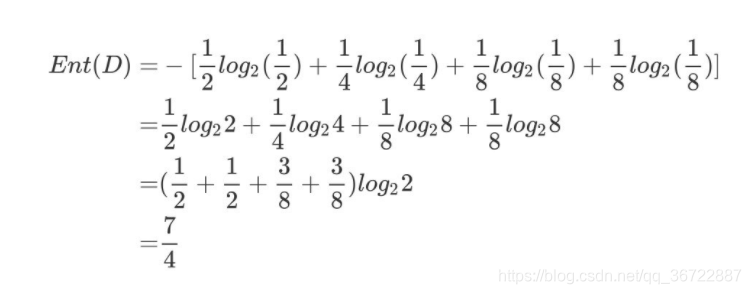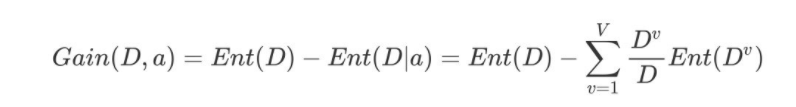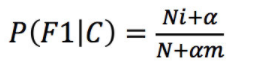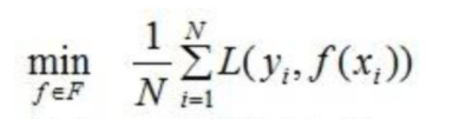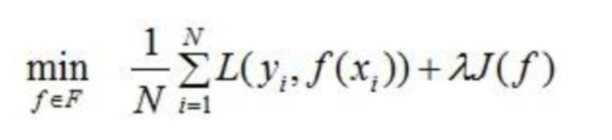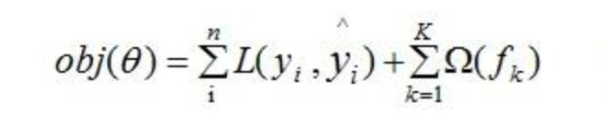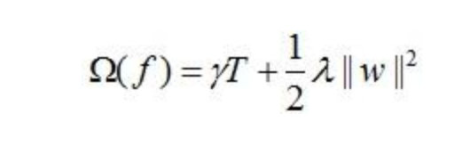目录
1 机器学习算法原理介绍
-
判别模型(discriminative model)
已知输入变量x,通过求解条件概率分布P(y|x)或者直接计算y的值来预测y。
例如:
- 线性回归(Linear Regression)
- 逻辑回归(Logistic Regression)
- 支持向量机(SVM)
- 传统神经网络(Traditional Neural Networks)
- 线性判别分析(Linear Discriminative Analysis)
- 条件随机场(Conditional Random Field)
-
生成模型(generative model)
已知输入变量x,通过对观测值和标注数据计算联合概率分布P(x,y)来达到判定估算y的目的。
例如:
- 朴素贝叶斯(Naive Bayes)
- 隐马尔科夫模型(HMM)
- 贝叶斯网络(Bayesian Networks)
- 隐含狄利克雷分布(Latent Dirichlet Allocation)
1.1 K-近邻算法
1 定义
K Nearest Neighbor算法又叫KNN算法,如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
2 算法流程
1)计算已知类别数据集中的点与当前点之间的距离
2)按距离递增次序排序
3)选取与当前点距离最小的k个点
4)统计前k个点所在的类别出现的频率(分类:样本出现最多个数 回归:K个杨样本的平均值)
5)返回前k个点出现频率最高的类别作为当前点的预测分类
1 K值选择
K值的减小就意味着整体模型变得复杂,容易发生过拟合;
K值的增大就意味着整体模型变得简单,容易发生欠拟合;
注:实际应用中,K值一般取一个比较小的数值,例如采用交叉验证来选择最优的K值。
2 误差估计
- 近似误差:对训练集的训练误差,关注训练集,近似误差小可能出现过拟合。
- 估计误差:对测试集的测试误差,关注测试集,估计误差小说明对未知数据的预测能力好。
3 K-近邻实现
-
线性扫描(穷举搜索)
计算输入实例与每一个训练实例的距离。计算后再查找K近邻。当训练集很大时,计算非常耗时。
-
KD树
-
一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构
-
kd树是一种二叉树,表示对k维空间的一个划分,构造kd树相当于不断地用垂直于坐标轴的超平面将K维空间切分,构成一系列的K维超矩形区域。kd树的每个结点对应于一个k维超矩形区域。
-
利用kd树可以省去对大部分数据点的搜索,从而减少搜索的计算量。
-
-
距离计算
-
欧式距离(Euclidean Distance)
-
曼哈顿距离(Manhattan Distance)
-
切比雪夫距离 (Chebyshev Distance)
-
闵可夫斯基距离(Minkowski Distance)
其中p是一个变参数:
- 当p=1时,就是曼哈顿距离;
- 当p=2时,就是欧氏距离;
- 当p→∞时,就是切比雪夫距离。
根据p的不同,闵氏距离可以表示某一类/种的距离。
其它距离:标准化欧氏距离 (Standardized EuclideanDistance)、余弦距离(Cosine Distance)、汉明距离(Hamming Distance)、杰卡德距离(Jaccard Distance)、马氏距离(Mahalanobis Distance)。
-
总结
闵氏距离的缺点:
-
将各个分量的量纲(scale),也就是“单位”相同的看待了;
-
未考虑各个分量的分布(期望,方差等)可能是不同的。
-
-
4 拓展:fit()、tansform()、fit_transform()区别
fit(): Method calculates the parameters μ and σ and saves them as internal objects.
解释:简单来说,就是求得训练集X的均值,方差,最大值,最小值,这些训练集X固有的属性。transform(): Method using these calculated parameters apply the transformation to a particular dataset.
解释:在fit的基础上,进行标准化,降维,归一化等操作(看具体用的是哪个工具,如PCA,StandardScaler等)。fit_transform(): joins the fit() and transform() method for transformation of dataset.
解释:fit_transform是fit和transform的组合,既包括了训练又包含了转换。transform()和fit_transform()二者的功能都是对数据进行某种统一处理(比如标准化~N(0,1),将数据缩放(映射)到某个固定区间,归一化,正则化等)fit_transform(trainData)对部分数据先拟合fit,找到该part的整体指标,如均值、方差、最大值最小值等等(根据具体转换的目的),然后对该trainData进行转换transform,从而实现数据的标准化、归一化等等。
5 K近邻算法优缺点
- 优点:
- 简单有效
- 重新训练的代价低
- 适合类域交叉样本
- KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合。
- 适合大样本自动分类
- 该算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量较小的类域采用这种算法比较容易产生误分。
- 缺点:
- 惰性学习
- KNN算法是懒散学习方法(lazy learning,基本上不学习),一些积极学习的算法要快很多
- 类别评分不是规格化
- 不像一些通过概率评分的分类
- 输出可解释性不强
- 例如决策树的输出可解释性就较强
- 对不均衡的样本不擅长
- 当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。该算法只计算“最近的”邻居样本,某一类的样本数量很大,那么或者这类样本并不接近目标样本,或者这类样本很靠近目标样本。无论怎样,数量并不能影响运行结果。可以采用权值的方法(和该样本距离小的邻居权值大)来改进。
- 计算量较大
- 目前常用的解决方法是事先对已知样本点进行剪辑,事先去除对分类作用不大的样本。
- 惰性学习
1.2 线性回归
1 定义
利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。
2 API案例
from sklearn.linear_model import LinearRegression
x = [[80, 86],
[82, 80],
[85, 78],
[90, 90],
[86, 82],
[82, 90],
[78, 80],
[92, 94]]
y = [84.2, 80.6, 80.1, 90, 83.2, 87.6, 79.4, 93.4]
# 实例化API
estimator = LinearRegression()
# 使用fit方法进行训练
estimator.fit(x,y)
print('回归系数:\n', estimator.coef_)
print('预测结果:\n', estimator.predict([[100, 80]]))
3 线性回归的损失和优化
-
1 总损失函数:(
最小二乘法)- yi为第i个训练样本的真实值
- h(xi)为第i个训练样本特征值组合预测函数
- 又称最小二乘法
-
2 优化算法:
-
2.1 正规方程
- X为特征值矩阵
- y为目标值矩阵
缺点:当特征过多过复杂时,求解速度太慢并且得不到结果
from sklearn.linear_model import LinearRegression from sklearn.preprocessing import StandardScaler from sklearn.metrics import mean_squared_error def linear_model1(): """ 线性回归:正规方程 :return:None """ # 1.获取数据 data = load_boston() # 2.数据集划分 x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22) # 3.特征工程-标准化 transfer = StandardScaler() x_train = transfer.fit_transform(x_train) x_test = transfer.fit_transform(x_test) # 4.机器学习-线性回归(正规方程) # fit_intercept:是否计算偏置; estimator = LinearRegression(fit_intercept=True) estimator.fit(x_train, y_train) # 5.模型评估 # 5.1 获取系数等值 y_predict = estimator.predict(x_test) print("预测值为:\n", y_predict) print("模型中的回归系数为:\n", estimator.coef_) print("模型中的偏置为:\n", estimator.intercept_) # 5.2 评价 # 均方误差 error = mean_squared_error(y_test, y_predict) print("误差为:\n", error) return None均方误差(Mean Squared Error)MSE)评价机制:
-
2.2 梯度下降法(Gradient Descent)
α为学习率或者步长
- 梯度
- 在
单变量函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率; - 在
多变量函数中,梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向;
- 在
算法选择依据:
- 小规模数据:
- 正规方程:LinearRegression(不能解决拟合问题)
- 岭回归
- 大规模数据:
- 梯度下降法:SGDRegressor
from sklearn.linear_model import SGDRegressor from sklearn.preprocessing import StandardScaler from sklearn.metrics import mean_squared_error def linear_model2(): """ 线性回归:梯度下降法 :return:None """ # 1.获取数据 data = load_boston() # 2.数据集划分 x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22) # 3.特征工程-标准化 transfer = StandardScaler() x_train = transfer.fit_transform(x_train) x_test = transfer.fit_transform(x_test) # 4.机器学习-线性回归(特征方程) # loss:损失类型 loss=”squared_loss”: 普通最小二乘法 # fit_intercept:是否计算偏置 # learning_rate: 学习率 # 'constant': eta = eta0 # 'optimal': eta = 1.0 / (alpha * (t + t0)) [default] # 'invscaling': eta = eta0 / pow(t, power_t) # power_t=0.25:存在父类当中 # 对于一个常数值的学习率来说,可以使用learning_rate=’constant’ ,并使用eta0来指定学习率。 estimator = SGDRegressor(loss="squared_loss",fit_intercept=True,max_iter=1000,learning_rate="constant",eta0=0.1) estimator.fit(x_train, y_train) # 5.模型评估 # 5.1 获取系数等值 y_predict = estimator.predict(x_test) print("预测值为:\n", y_predict) print("模型中的系数为:\n", estimator.coef_) print("模型中的偏置为:\n", estimator.intercept_) # 5.2 评价 # 均方误差 error = mean_squared_error(y_test, y_predict) print("误差为:\n", error) return None - 梯度
-
4 概念解释
5 梯度下降算法
-
全梯度下降算法(Full gradient descent)-
在更新参数时使用所有的样本来进行更新
-
计算训练集所有样本误差,对其求和再取平均值作为目标函数。
缺点:
-
因为在执行每次更新时,我们需要在
整个数据集上计算所有的梯度,所以批梯度下降法的速度会很慢,同时,批梯度下降法无法处理超出内存容量限制的数据集。 -
批梯度下降法同样也不能在线更新模型,即在
运行的过程中,不能增加新的样本。
-
-
随机梯度下降算法(Stochastic gradient descent)- 每次只代入计算一个样本目标函数的梯度来更新权重,再取下一个样本重复此过程,直到损失函数值停止下降或损失函数值小于某个可以容忍的阈值。
优点:此过程简单,高效,通常可以较好地避免更新迭代收敛到局部最优解。
缺点:由于SG每次只使用一个样本迭代,若遇上噪声则容易陷入局部最优解。
-
小批量梯度下降算法(Mini-batch gradient descent)- 每次从训练样本集上随机抽取一个小样本集,在抽出来的小样本集上采用FG迭代更新权重。
小批量梯度下降算法是FG和SG的折中方案,在一定程度上兼顾了以上两种方法的优点。
batch_size:被抽出的小样本集所含样本点的个数,通常设置为2的幂次方,利于GPU加速处理。
特别的,若batch_size=1,则变成了SG;若batch_size=n,则变成了FG.
-
随机平均梯度下降算法(Stochastic average gradient descent)- 在内存中为每一个样本都维护一个旧的梯度,随机选择第i个样本来更新此样本的梯度,其他样本的梯度保持不变,然后求得所有梯度的平均值,进而更新了参数。
在SG方法中,虽然避开了运算成本大的问题,但对于大数据训练而言,SG效果常不尽如人意,因为每一轮梯度更新都完全与上一轮的数据和梯度无关。SAG能克服该问题。
它们都是为了正确地调节权重向量,通过为每个权重计算一个梯度,从而更新权值,使目标函数尽可能最小化。其差别在于样本的使用方式不同。
6 欠拟合和过拟合原因及解决办法
- 1 欠拟合原因以及解决办法
- 原因:学习到数据的特征过少
- 解决办法:
- 1)
添加其他特征项,有时候我们模型出现欠拟合的时候是因为特征项不够导致的,可以添加其他特征项来很好地解决。例如,“组合”、“泛化”、“相关性”三类特征是特征添加的重要手段,无论在什么场景,都可以照葫芦画瓢,总会得到意想不到的效果。除上面的特征之外,“上下文特征”、“平台特征”等等,都可以作为特征添加的首选项。 - 2)
添加多项式特征,这个在机器学习算法里面用的很普遍,例如将线性模型通过添加二次项或者三次项使模型泛化能力更强。
- 1)
- 2 过拟合原因以及解决办法
- 原因:原始特征过多,存在一些嘈杂特征, 模型过于复杂是因为模型尝试去兼顾各个测试数据点
- 解决办法:
- 1)重新
清洗数据,导致过拟合的一个原因也有可能是数据不纯导致的,如果出现了过拟合就需要我们重新清洗数据。 - 2)
增大数据的训练量,还有一个原因就是我们用于训练的数据量太小导致的,训练数据占总数据的比例过小。 - 3)
正则化 - 4)减少特征维度,防止
维灾难
- 1)重新
7 正则化(解决过拟合问题)
-
在学习的时候,数据提供的特征有些影响模型复杂度或者这个特征的数据点异常较多,所以算法在学习的时候尽量减少这个特征的影响(甚至删除某个特征的影响)
-
正则化类别
from sklearn.linear_model import Ridge, ElasticNet, Lasso -
L1正则化-
作用:可以使得其中一些权重直接为0,删除这个特征的影响
-
LASSO回归(正则项为权值向量的ℓ1范数)代价函数如下:
-
Lasso Regression 能够自动进行特征选择,并输出一个稀疏模型(只有少数特征的权重是非零的)。
-
L2正则化-
作用:可以使得其中一些权重都很小,都接近于0,削弱某个特征的影响
-
优点:越小的参数说明模型越简单,越简单的模型则越不容易产生过拟合现象
-
Ridge回归(实现了SAG)代价函数如下:
-
# alpha:正则化力度,也叫 λ λ取值:0~1 1~10;
# solver:会根据数据自动选择优化方法
# sag:如果数据集、特征都比较大,选择该随机梯度下降优化
# normalize:数据是否进行标准化
# normalize=False:可以在fit之前调用preprocessing.StandardScaler标准化数据
# Ridge.coef_:回归权重
# Ridge.intercept_:回归偏置
sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver="auto", normalize=False)
-
Elastic Net (弹性网络)弹性网络在岭回归和Lasso回归中进行了折中,通过混合比(mix ratio) r 进行控制:
- r=0:弹性网络变为岭回归
- r=1:弹性网络便为Lasso回归
弹性网络的代价函数 :
回归模型选择:
- 常用:岭回归
- 假设只有少部分特征是有用的:
- 弹性网络
- Lasso
- 一般来说,弹性网络的使用更为广泛。因为在特征维度高于训练样本数,或者特征是强相关的情况下,Lasso回归的表现不太稳定。
在高维空间中,大多数训练数据驻留在定义特征空间的超立方体的角落中。
所需的训练实例数量随着使用的维度数量呈指数增长。
-
8 sklearn模型的保存和加载API
from sklearn.externals import joblib def load_dump_demo(): """ 模型保存和加载 :return: """ # 1.获取数据 data = load_boston() # 2.数据集划分 x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22) # 3.特征工程-标准化 transfer = StandardScaler() x_train = transfer.fit_transform(x_train) x_test = transfer.fit_transform(x_test) # 4.机器学习-线性回归(岭回归) # # 4.1 模型训练 # estimator = Ridge(alpha=1) # estimator.fit(x_train, y_train) # # # 4.2 模型保存 # joblib.dump(estimator, "./data/test.pkl") # 4.3 模型加载 estimator = joblib.load("./data/test.pkl") # 5.模型评估 # 5.1 获取系数等值 y_predict = estimator.predict(x_test) print("预测值为:\n", y_predict) print("模型中的系数为:\n", estimator.coef_) print("模型中的偏置为:\n", estimator.intercept_) # 5.2 评价 # 均方误差 error = mean_squared_error(y_test, y_predict) print("误差为:\n", error)
1.3 逻辑回归
逻辑回归(Logistic Regression)是机器学习中的一种分类模型,逻辑回归是一种分类算法,逻辑回归就是解决二分类问题的利器。
算法原理:将线性回归的输出作为逻辑回归的输入,然后经过sigmoid函数变换将整体的值映射到[0,1],再设定阈值进行分类。
from klearn.linear_models import LogisticRegression
# solver可选参数:{'liblinear', 'sag', 'saga','newton-cg', 'lbfgs'},
# 对于小数据集来说,“liblinear”是个不错的选择,而“sag”和'saga'对于大型数据集会更快。
# 对于多类问题,只有'newton-cg', 'sag', 'saga'和'lbfgs'可以处理多项损失;“liblinear”仅限于“one-versus-rest”分类。
# penalty:正则化的种类
# C:正则化力度
estimator = LogisticRegression(solver='liblinear', penalty=‘l2’, C = 1.0)
1 总损失函数(对数似然损失)
2 概念解释
准确率:所有样本中预测对的比例
精确率:预测结果为正例样本中真实为正例的比例(预测为正的样本中的正样本)
召回率:真实为正例的样本中预测结果为正例的比例(正样本中预测为正的样本)
F1-score:反映模型的稳健性
from sklearn.metrics import classification_report
# labels:指定类别对应的数字 target_names:目标类别名称 return:每个类别精确率与召回率
ret = classification_report(y_test, y_predict, labels=(2,4), target_names=("良性", "恶性"))
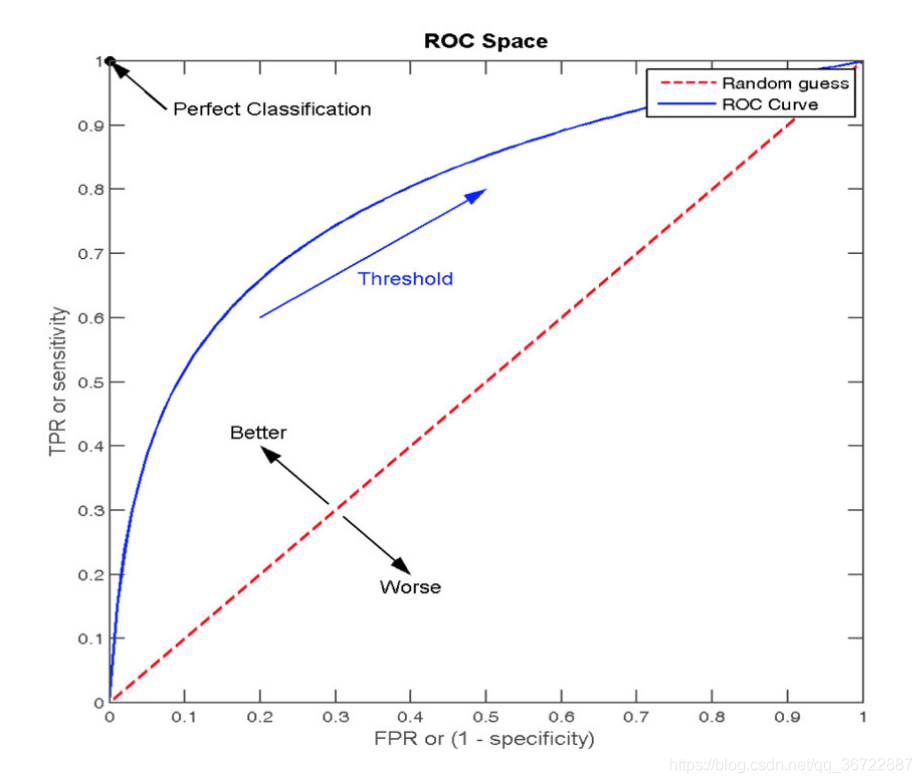
3 ROC曲线
- TPR = TP / (TP + FN) <
击中率>- 所有真实类别为1的样本中,预测类别为1的比例
- FPR = FP / (FP + TN) <
虚惊率>- 所有真实类别为0的样本中,预测类别为1的比例
-
AUC指标
- AUC的概率意义是随机取一对正负样本,正样本得分大于负样本得分的概率
- AUC的范围在[0, 1]之间,并且越接近1越好,越接近0.5属于乱猜
- AUC=1,完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
- 0.5<AUC<1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
-
API
from sklearn.metrics import roc_auc_score # 计算所得为ROC曲线面积 roc_auc_score(y_test, y_predict)
4 样本不均衡问题
-
增加一些少数类样本使得正、反例数目接近,然后再进行学习。
-
关于类别不平衡的问题,主要有两种处理方式:
-
1 过采样方法
- 增加数量较少那一类样本的数量,使得正负样本比例均衡。
# 使用imblearn进行随机过采样 from imblearn.over_sampling import RandomOverSampler ros = RandomOverSampler(random_state=0)-
1.1 过采样经典方法
-
1 随机过采样法
通过复制所选择的样本生成样本集
缺点:易产生模型过拟合问题
-
2 SMOTE算法
(Synthetic Minority Oversampling,合成少数类过采样技术)
-
对每个少数类样本,从它的最近邻中随机选择一个样本,然后在两个样本之间的连线上随机选择一点作为新合成的少数类样本。
-
SMOTE算法摒弃了随机过采样复制样本的做法,可以防止随机过采样中容易过拟合的问题,实践证明此方法可以提高分类器的性能。
# SMOTE过采样 from imblearn.over_sampling import SMOTE X_resampled, y_resampled = SMOTE().fit_resample(X, y) -
-
-
2 欠采样方法
- 减少数量较多那一类样本的数量,使得正负样本比例均衡。
# 随机欠采样 from imblearn.under_sampling import RandomUnderSampler rus = RandomUnderSampler(random_state=0)缺点:
- 随机欠采样方法通过改变多数类样本比例以达到修改样本分布的目的,从而使样本分布较为均衡,但由于采样的样本集合要少于原来的样本集合,因此会造成一些信息缺失,即将多数类样本删除有可能会导致分类器丢失有关多数类的重要信息。
-
1.4 决策树算法
决策树思想的来源非常朴素,程序设计中的条件分支结构就是if-else结构,最早的决策树就是利用这类结构分割数据的一种分类学习方法
- 是一种树形结构,本质是一颗由多个判断节点组成的树
- 其中每个内部节点表示一个属性上的判断,
- 每个分支代表一个判断结果的输出,
- 最后每个叶节点代表一种分类结果。
1 信息增益、信息增益率和基尼系数
信息熵(information entropy):度量样本集合纯度最常用的一种指标。
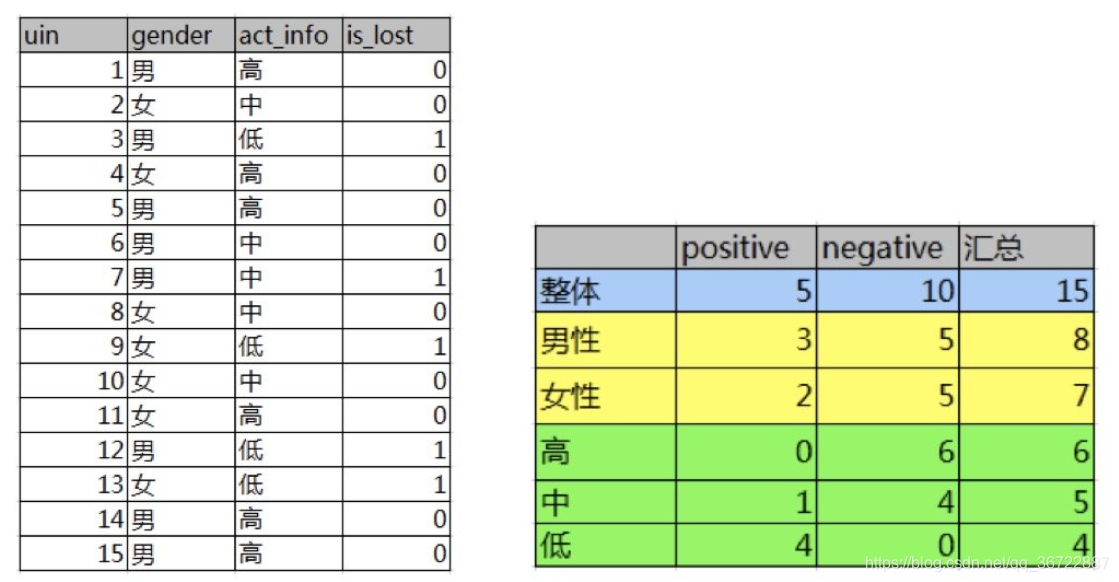
篮球比赛里,有4个球队 {A,B,C,D} ,获胜概率分别为{1/2, 1/4, 1/8, 1/8},求Ent(D)
信息增益(information gain):以某特征划分数据集前后的熵的差值,用来衡量使用当前特征对于样本集合D划分效果的好坏。
2 信息熵计算案例
1.5 集成算法
1 定义
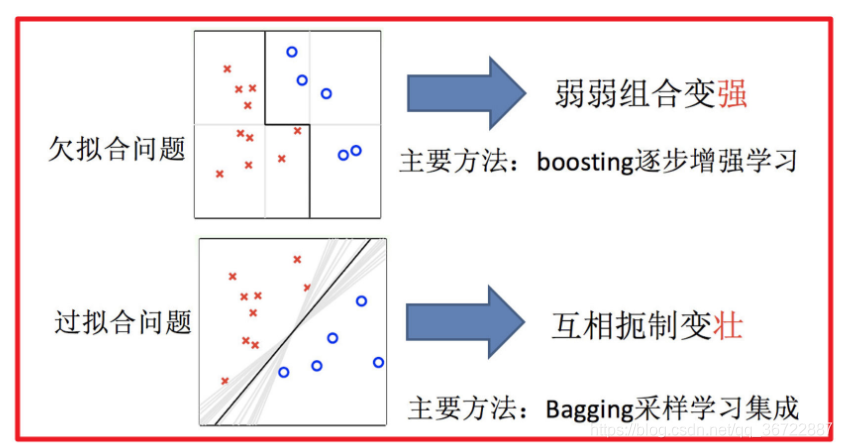
通过建立几个模型来解决单一预测问题。它的工作原理是生成多个分类器/模型,各自独立地学习和作出预测。这些预测最后结合成组合预测,因此优于任何一个单分类的做出预测。
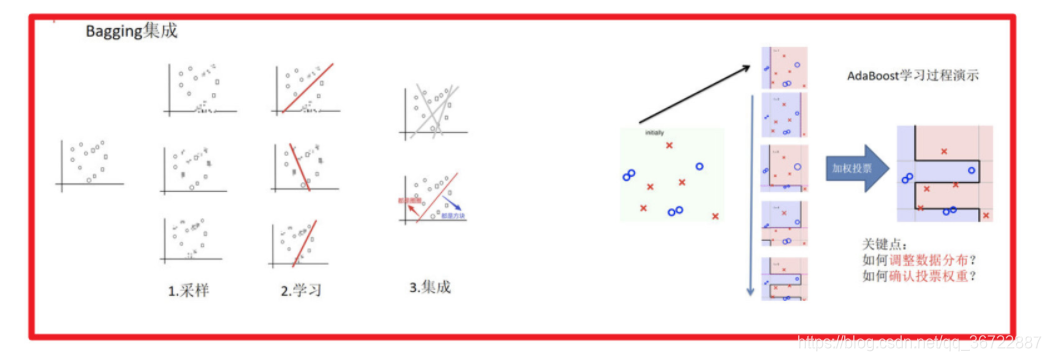
2 集成学习中boosting和Bagging
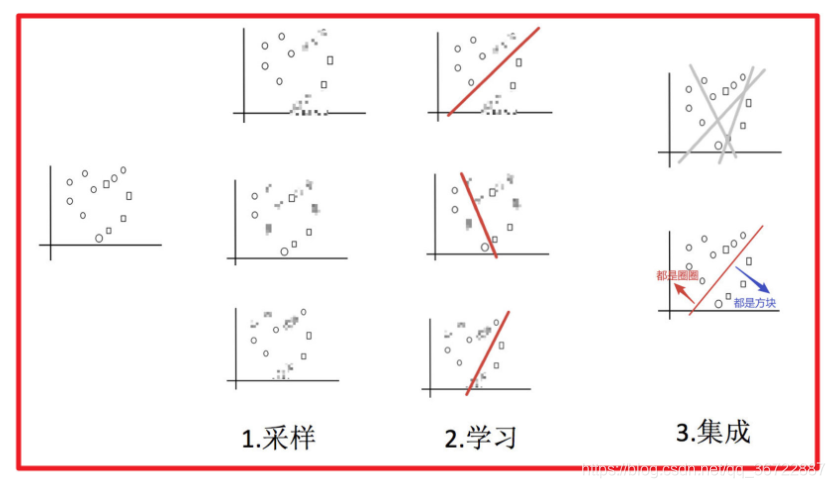
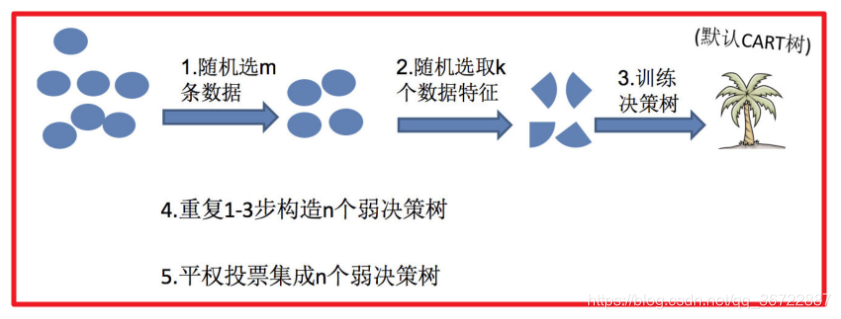
3 Bagging及随机森林
1) 采样不同数据集
2) 训练分类器
3) 平权投票,获取最终结果
Bagging + 决策树/线性回归/逻辑回归/深度学习… = bagging集成学习方法
-
随机森林
随机森林 = Bagging + 决策树
包外数据:没有选择到的数据,称之为 Out-of-bag(OOB)数据,当数据足够多,对于任意一组数据是包外数据的概率为1/e。
经验证,包外估计是对集成分类器泛化误差的无偏估计.
-
API实现
# n_estimators:(default = 10)森林里的树木数量 # Criterion:(default =“gini”) 分割特征的测量方法 # max_features="auto”,每个决策树的最大特征数量 """ If "auto", then max_features=sqrt(n_features). If "sqrt", then max_features=sqrt(n_features)(same as "auto"). If "log2", then max_features=log2(n_features). If None, then max_features=n_features. """ # bootstrap:(default = True) 是否在构建树时使用放回抽样 # min_samples_split 内部节点再划分所需最小样本数 # min_samples_leaf 叶子节点的最小样本数 # min_impurity_split: 节点划分最小不纯度 sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True, random_state=None, min_samples_split=2)
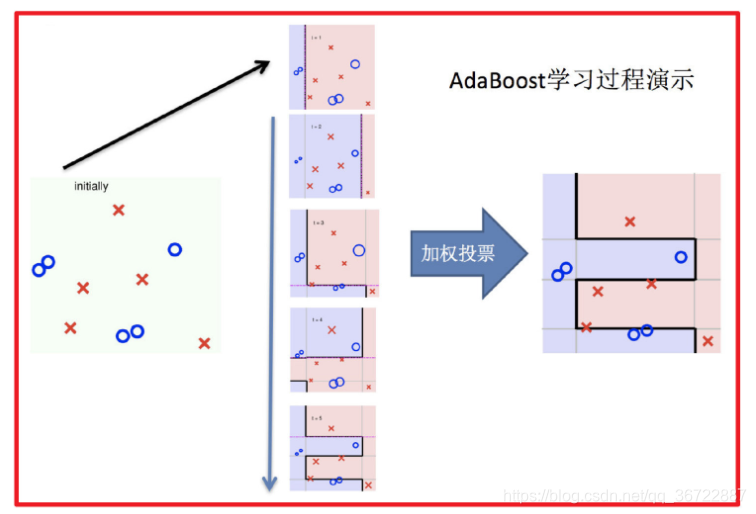
4 boosting
- 定义
每新加入一个弱学习器,整体能力就会得到提升,代表算法有:Adaboost,GBDT,XGBoost,LightGBM
- 算法步骤
- 1)训练第一个学习器
- 2)调整数据分布
- 3)训练第二个学习器
- 4)再次调整数据分布
- 5)依次训练学习器,调整数据分布
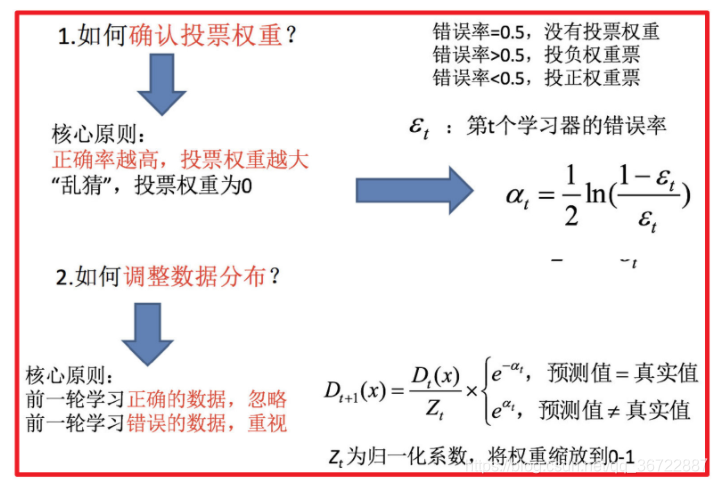
Bagging集成与Boosting集成的区别
- 区别一:数据方面
- Bagging:对数据进行采样训练;
- Boosting:根据前一轮学习结果调整数据的重要性。
- 区别二:投票方面
- Bagging:所有学习器平权投票;
- Boosting:对学习器进行加权投票。
- 区别三:学习顺序
- Bagging的学习是并行的,每个学习器没有依赖关系;
- Boosting学习是串行,学习有先后顺序。
- 区别四:主要作用
- Bagging主要用于提高泛化性能(解决过拟合,也可以说降低方差)
- Boosting主要用于提高训练精度 (解决欠拟合,也可以说降低偏差)
- AdaBoost
- 原理图
from sklearn.ensemble import AdaBoostClassifier
-
GBDT
-
GBDT 的全称是 Gradient Boosting Decision Tree,梯度提升树,在传统机器学习算法中,GBDT算的上TOP3的算法。
-
GBDT使用的决策树是CART回归树
-
无论是处理回归问题还是二分类以及多分类,GBDT使用的决策树通通都是都是CART回归树。
-
在这里插入图片描述
1.6 聚类算法
1 定义
一种典型的无监督学习算法,主要用于将相似的样本自动归到一个类别中。
在聚类算法中根据样本之间的相似性,将样本划分到不同的类别中,对于不同的相似度计算方法,会得到不同的聚类结果,常用的相似度计算方法有欧式距离法。
2 算法学习
- 1)随机设置K个特征空间内的点作为初始的聚类中心
- 2)对于其他每个点计算到K个中心的距离,未知的点选择最近的一个聚类中心点作为标记类别
- 3)接着对着标记的聚类中心之后,重新计算出每个聚类的新中心点(平均值)
- 4)如果计算得出的新中心点与原中心点一样(质心不再移动),那么结束,否则重新进行第二步过程
3 API
# n_clusters:开始的聚类中心数量
# 参数
# estimator.fit(x)
# estimator.predict(x)
# estimator.fit_predict(x)
sklearn.cluster.KMeans(n_clusters=8)
4 案例分析
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import calinski_harabaz_score
# 创建数据集
# X为样本特征,Y为样本簇类别, 共1000个样本,每个样本2个特征,共4个簇,
# 簇中心在[-1,-1], [0,0],[1,1], [2,2], 簇方差分别为[0.4, 0.2, 0.2, 0.2]
X, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1, -1], [0, 0], [1, 1], [2, 2]],
cluster_std=[0.4, 0.2, 0.2, 0.2],
random_state=9)
# 数据集可视化
plt.scatter(X[:, 0], X[:, 1], marker='o')
plt.show()
y_pred = KMeans(n_clusters=2, random_state=9).fit_predict(X)
# 分别尝试n_cluses=2\3\4,然后查看聚类效果
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()
# 用Calinski-Harabasz Index评估的聚类分数
print(calinski_harabaz_score(X, y_pred))
5 模型评估
- SSE
- 误差平方和的值越小越好
- 肘部法
- 下降率突然变缓时即认为是最佳的k值
- SC系数
- 取值为[-1, 1],其值越大越好
- CH系数
- 分数s高则聚类效果越好
- CH需要达到的目的:用尽量少的类别聚类尽量多的样本,同时获得较好的聚类效果。
6 K-Means
-
K-Means算法优缺点总结
- 优点:
- 1.原理简单(靠近中心点),实现容易
- 2.聚类效果中上(依赖K的选择)
- 3.空间复杂度o(N),时间复杂度o(IKN)
- 缺点:
- 1.对离群点,噪声敏感 (中心点易偏移)
- 2.很难发现大小差别很大的簇及进行增量计算
- 3.结果不一定是全局最优,只能保证局部最优(与K的个数及初值选取有关)
- 优点:
-
优化方法
| 优化方法 | 思路 |
|---|---|
| Canopy+kmeans | Canopy粗聚类配合kmeans |
| kmeans++ | 距离越远越容易成为新的质心 |
| 二分k-means | 拆除SSE最大的簇 |
| k-medoids | 和kmeans选取中心点的方式不同 |
| kernel kmeans | 映射到高维空间 |
| ISODATA | 动态聚类,可以更改K值大小 |
| Mini-batch K-Means | 大数据集分批聚类 |
1.7 朴素贝叶斯
1 定义
- 朴素贝叶斯:假定了特征与特征之间相互独立的贝叶斯公式
- 朴素:假定了特征与特征相互独立
- 如果一个事物在一些属性条件发生的情况下,事物属于A的概率>属于B的概率,则判定事物属于A。
2 算法原理
- 分解各类先验样本数据中的特征;
- 计算各类数据中,各特征的条件概率;(比如:特征1出现的情况下,属于A类的概率p(A|特征1),属于B类的概率p(B|特征1),属于C类的概率p(C|特征1)…)
- 分解待分类数据中的特征(特征1、特征2、特征3、特征4…)
- 计算各特征的各条件概率的乘积,如下所示:
判断为A类的概率:p(A|特征1) * p(A|特征2) * p(A|特征3) * p(A|特征4)…
判断为B类的概率:p(B|特征1) * p(B|特征2) * p(B|特征3) * p(B|特征4)…
判断为C类的概率:p(C|特征1) * p(C|特征2) * p(C|特征3) * p(C|特征4)…
… - 结果中的最大值就是该样本所属的类别
3 拉普拉斯平滑
-
问题:从下面的例子的到娱乐概率为0,这是不合理的,如果词频列表里面有很多出现次数为0,很可能计算结果都为0。
-
解决方法:拉普拉斯平滑
a为指定的系数一般为1,m为训练文档中统计出的特征词个数
4 案例实现
商品评论情感分析
- 1)获取数据
- 2)数据基本处理
- 2.1) 取出内容列,对数据进行分析
- 2.2) 判定评判标准
- 2.3) 选择停用词
- 2.4) 把内容处理,转化成标准格式
- 2.5) 统计词的个数
- 2.6)准备训练集和测试集
- 3)模型训练
- 4)模型评估
import pandas as pd
import numpy as np
import jieba
import matplotlib.pyplot as plt
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
# 加载数据
data = pd.read_csv("./data/书籍评价.csv", encoding="gbk")
# 数据基本处理
# 2.1) 取出内容列,对数据进行分析
content = data["内容"]
# 2.2) 判定评判标准 -- 1好评;0差评
data.loc[data.loc[:, '评价'] == "好评", "评论标号"] = 1 # 把好评修改为1
data.loc[data.loc[:, '评价'] == '差评', '评论标号'] = 0
# data.head()
good_or_bad = data['评价'].values # 获取数据
print(good_or_bad)
# ['好评' '好评' '好评' '好评' '差评' '差评' '差评' '差评' '差评' '好评' '差评' '差评' '差评']
# 2.3) 选择停用词
# 加载停用词
stopwords=[]
with open('./data/stopwords.txt','r',encoding='utf-8') as f:
lines=f.readlines()
print(lines)
for tmp in lines:
line=tmp.strip()
print(line)
stopwords.append(line)
# stopwords # 查看新产生列表
#对停用词表进行去重
stopwords=list(set(stopwords))#去重 列表形式
print(stopwords)
# 2.4) 把“内容”处理,转化成标准格式
comment_list = []
for tmp in content:
print(tmp)
# 对文本数据进行切割
# cut_all 参数默认为 False,所有使用 cut 方法时默认为精确模式
seg_list = jieba.cut(tmp, cut_all=False)
print(seg_list) # <generator object Tokenizer.cut at 0x0000000007CF7DB0>
seg_str = ','.join(seg_list) # 拼接字符串
print(seg_str)
comment_list.append(seg_str) # 目的是转化成列表形式
# print(comment_list) # 查看comment_list列表。
# 2.5) 统计词的个数
# 进行统计词个数
# 实例化对象
# CountVectorizer 类会将文本中的词语转换为词频矩阵
con = CountVectorizer(stop_words=stopwords)
# 进行词数统计
X = con.fit_transform(comment_list) # 它通过 fit_transform 函数计算各个词语出现的次数
name = con.get_feature_names() # 通过 get_feature_names()可获取词袋中所有文本的关键字
print(X.toarray()) # 通过 toarray()可看到词频矩阵的结果
print(name)
# 2.6)准备训练集和测试集
# 准备训练集 这里将文本前10行当做训练集 后3行当做测试集
x_train = X.toarray()[:10, :]
y_train = good_or_bad[:10]
# 准备测试集
x_text = X.toarray()[10:, :]
y_text = good_or_bad[10:]
# 模型训练
# 构建贝叶斯算法分类器
mb = MultinomialNB(alpha=1) # alpha 为可选项,默认 1.0,添加拉普拉修/Lidstone 平滑参数
# 训练数据
mb.fit(x_train, y_train)
# 预测数据
y_predict = mb.predict(x_text)
#预测值与真实值展示
print('预测值:',y_predict)
print('真实值:',y_text)
# 模型评估
print(mb.score(x_text, y_text))
1.8 支持向量机
1 基本元素
-
【data】数据
-
【classifier】分类
-
【optimization】最优化
-
【kernelling】核方法
-
【hyperplane】超平面
2 基本思想
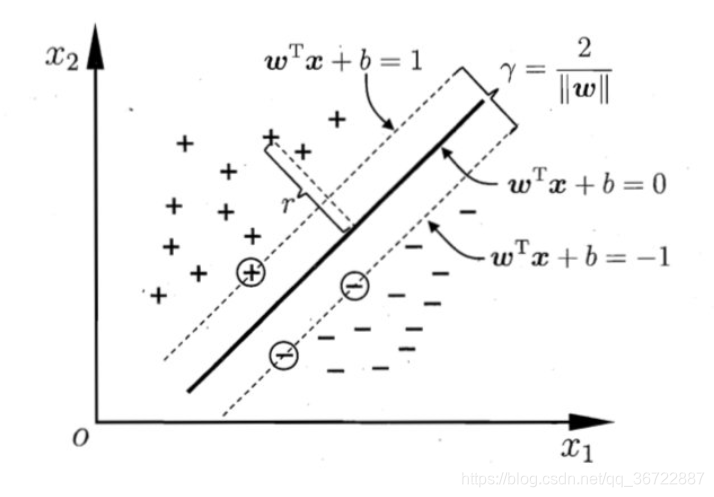
SVM(supported vector machine,支持向量机),即寻找到一个超平面使样本分成两类,并且间隔最大。
3 用途
-
线性或非线性分类、回归,甚至是异常值检测
-
特别适用于中小型复杂数据集的分类
4 硬间隔和软间隔
硬间隔:严格地让所有实例都不在最大间隔之间,并且位于正确的一边。它只在数据是线性可分离的时候才有效;其次,它对异常值非常敏感。
软间隔:尽可能在保持最大间隔宽阔和限制间隔违例(即位于最大间隔之上,甚至在错误的一边的实例)之间找到良好的平衡。
5 支持向量机推导
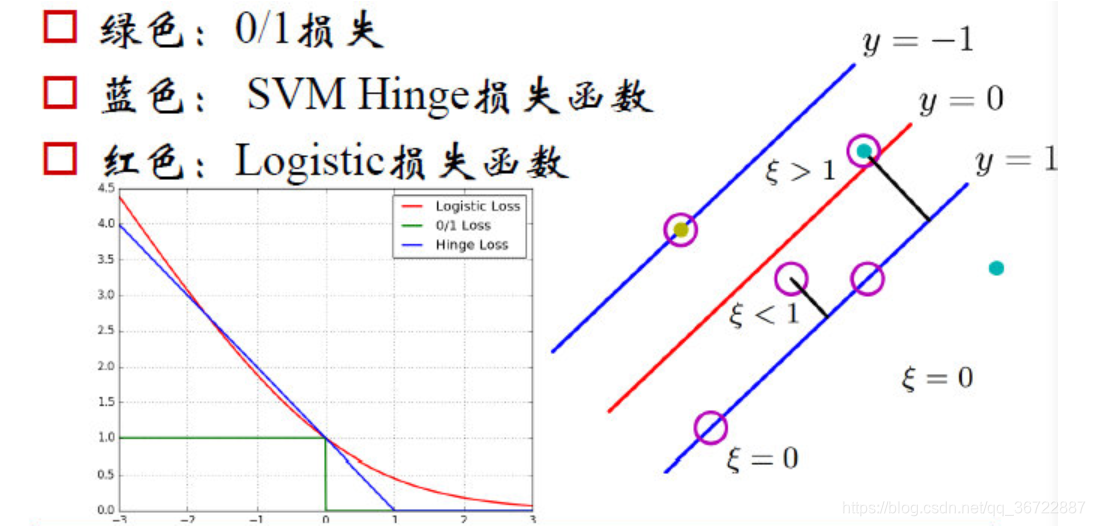
6 损失函数
SVM Hinge损失(折页损失函数、铰链损失函数)
7 SVM回归
让尽可能多的实例位于预测线上,同时限制间隔违例(也就是不在预测线距上的实例)。
sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3,coef0=0.0,random_state=None)
"""
C:
惩罚系数,用来控制损失函数的惩罚系数,类似于线性回归中的正则化系数。
- C越大,相当于惩罚松弛变量,希望松弛变量接近0,即**对误分类的惩罚增大**,趋向于对训练集全分对的情况,这样会出现训练集测试时准确率很高,但泛化能力弱,容易导致过拟合。
- C值小,对误分类的惩罚减小,容错能力增强,泛化能力较强,但也可能欠拟合。
- kernel:
算法中采用的核函数类型,核函数是用来将非线性问题转化为线性问题的一种方法。
- 参数选择有RBF, Linear, Poly, Sigmoid或者自定义一个核函数。
- 默认的是"RBF",即径向基核,也就是高斯核函数;
- 而Linear指的是线性核函数,
- Poly指的是多项式核,
- Sigmoid指的是双曲正切函数tanh核;。
- degree:
- 当指定kernel为'poly'时,表示选择的多项式的最高次数,默认为三次多项式;
- 若指定kernel不是'poly',则忽略,即该参数只对'poly'有用。
- 多项式核函数是将低维的输入空间映射到高维的特征空间。
- coef0:核函数常数值(y=kx+b中的b值),
- 只有‘poly’和‘sigmoid’核函数有,默认值是0。
"""
sklearn.svm.LinearSVC(penalty='l2', loss='squared_hinge', dual=True, C=1.0)
"""
penalty:正则化参数,L1和L2两种参数可选,仅LinearSVC有。
loss:损失函数,有hinge和squared_hinge两种可选,前者又称L1损失,后者称为L2损失,默认是squared_hinge,其中hinge是SVM的标准损失,
squared_hinge是hinge的平方
dual:是否转化为对偶问题求解,默认是True。
C:惩罚系数,用来控制损失函数的惩罚系数,类似于线性回归中的正则化系数。
"""
8 SVM优缺点
- SVM的优点:
- 在高维空间中非常高效;
- 即使在数据维度比样本数量大的情况下仍然有效;
- 在决策函数(称为支持向量)中使用训练集的子集,因此它也是高效利用内存的;
- 通用性:不同的核函数与特定的决策函数一一对应;
- SVM的缺点:
- 如果特征数量比样本数量大得多,在选择核函数时要避免过拟合;
- 对缺失数据敏感;
- 对于核函数的高维映射解释力不强
1.9 EM算法
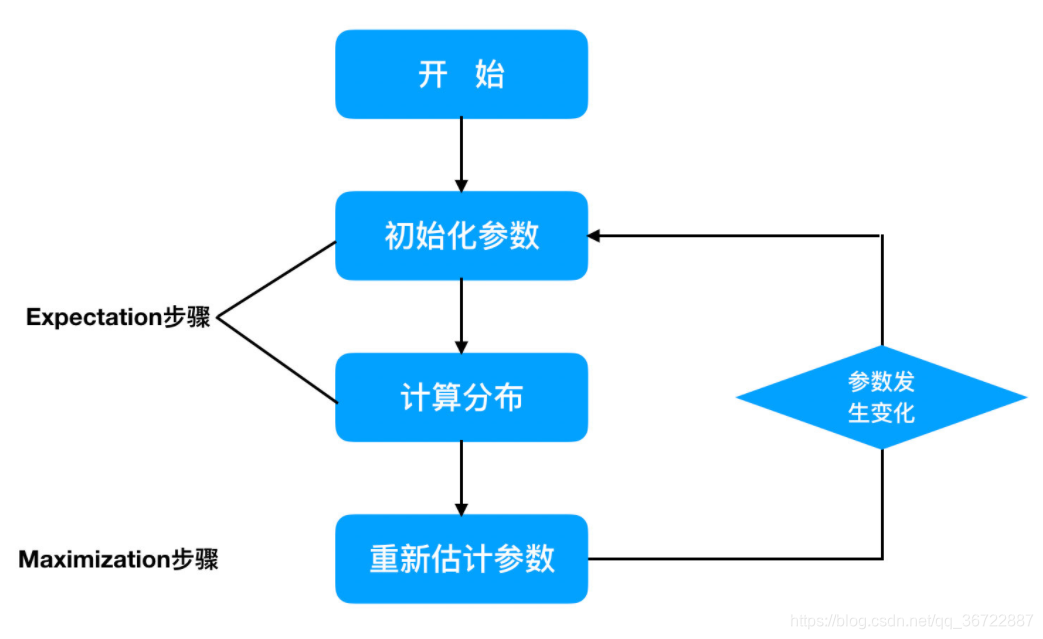
1 基本思想
- 首先根据己经给出的观测数据,估计出模型参数的值;
- 然后再依据上一步估计出的参数值估计缺失数据的值,再根据估计出的缺失数据加上之前己经观测到的数据重新再对参数值进行估计;
- 然后反复迭代,直至最后收敛,迭代结束。
2 算法流程
1.10 HMM模型
1 定义
隐马尔可夫模型(Hidden Markov Model,HMM)是统计模型,它用来描述一个含有隐含未知参数的马尔可夫过程。
马尔科夫链即为状态空间中从一个状态到另一个状态转换的随机过程。
马尔科夫链的无记忆性:下一状态的概率分布只能由当前状态决定,在时间序列中它前面的事件均与之无关。
2 常见术语
- 可见状态链
- 隐含状态链
- 转换概率
- 输出概率
3 HMM两个重要假设
1) 齐次马尔科夫链假设
- 即任意时刻的隐藏状态只依赖于它前一个隐藏状态。
2) 观测独立性假设
- 即任意时刻的观察状态只仅仅依赖于当前时刻的隐藏状态,这也是一个为了简化模型的假设。
4 HMM模型算法原理
一个HMM模型,可以由隐藏状态初始概率分布Π , 状态转移概率矩阵A和观测状态概率矩阵B决定。Π,A决定状态序列,B决定观测序列。
因此,HMM模型可以由一个三元组λ表示如下:
- λ=(A,B,Π)= (状态序列,观测序列,初始状态概率分布)
5 HMM模型三个基本问题
1)评估观察序列概率 —— 前向后向的概率计算
- 即给定
模型λ=(A,B,Π)和观测序列O={o_1,o_2,…o_T},计算在模型λ下某一个观测序列O出现的概率P(O|λ)。 - 这个问题的求解需要用到前向后向算法,是HMM模型三个问题中最简单的。
2)预测问题,也称为解码问题 ——维特比(Viterbi)算法
- 即给定
模型λ=(A,B,Π)和观测序列O={o_1,o_2,…o_T},求给定观测序列条件下,最可能出现的对应的状态序列。 - 这个问题的求解需要用到基于动态规划的维特比算法,是HMM模型三个问题中复杂度居中的算法。
3)模型参数学习问题 —— 鲍姆-韦尔奇(Baum-Welch)算法(状态未知) ,这是一个学习问题
- 即给定
观测序列O={o_1,o_2,…o_T},估计模型λ=(A,B,Π)的参数,使该模型下观测序列的条件概率P(O∣λ)最大。 - 这个问题的求解需要用到基于EM算法的鲍姆-韦尔奇算法,是HMM模型三个问题中最复杂的。
6 案例实现
import numpy as np
from hmmlearn import hmm
# 设定隐藏状态的集合
states = ["box 1", "box 2", "box3"]
n_states = len(states)
# 设定观察状态的集合
observations = ["red", "white"]
n_observations = len(observations)
# 设定初始状态分布
start_probability = np.array([0.2, 0.4, 0.4])
# 设定状态转移概率分布矩阵
transition_probability = np.array([
[0.5, 0.2, 0.3],
[0.3, 0.5, 0.2],
[0.2, 0.3, 0.5]
])
# 设定观测状态概率矩阵
emission_probability = np.array([
[0.5, 0.5],
[0.4, 0.6],
[0.7, 0.3]
])
# 设定模型参数
model = hmm.MultinomialHMM(n_components=n_states)
model.startprob_=start_probability # 初始状态分布
model.transmat_=transition_probability # 状态转移概率分布矩阵
model.emissionprob_=emission_probability # 观测状态概率矩阵
seen = np.array([[0,1,0]]).T # 设定观测序列
box = model.predict(seen)
print("球的观测顺序为:\n", ", ".join(map(lambda x: observations[x], seen.flatten())))
# 注意:需要使用flatten方法,把seen从二维变成一维
print("最可能的隐藏状态序列为:\n", ", ".join(map(lambda x: states[x], box)))
print(model.score(seen))
# 输出结果是:-2.03854530992
# 对数处理结果,概率值
import math
math.exp(model.score(seen))
# ln0.13022≈−2.0385
# 输出结果是:0.13021800000000003
1.11 xgboost算法
1 定义
XGBoost(Extreme Gradient Boosting)全名叫极端梯度提升树,XGBoost是集成学习方法的王牌,在Kaggle数据挖掘比赛中,大部分获胜者用了XGBoost。
2 最优模型构建方法
构建最优模型的一般方法是最小化训练数据的损失函数
-
经验风险最小化
训练得到的模型复杂度较高。当训练数据较小时,模型很容易出现过拟合问题。
-
结构风险最小化
结构风险最小化的模型往往对训练数据以及未知的测试数据都有较好的预测
3 目标函数
目标函数,即损失函数,通过最小化损失函数来构建最优模型。
其中yi是模型的实际输出结果,yi是模型的输出结果;
等式右边第一部分是模型的训练误差,第二部分是正则化项,这里的正则化项是K棵树的正则化项相加而来的。
-
XGBoost使用CART树,则树的复杂度为
其中T为叶子节点的个数,||w||为叶子节点向量的模 。γ表示节点切分的难度,λ表示L2正则化系数。
-
XGBoost的回归树构建方法
-
XGBoost与GDBT的区别
- 区别一:
- XGBoost生成CART树考虑了树的复杂度,
- GDBT未考虑,GDBT在树的剪枝步骤中考虑了树的复杂度。
- 区别二:
- XGBoost是拟合上一轮损失函数的二阶导展开,GDBT是拟合上一轮损失函数的一阶导展开,因此,XGBoost的准确性更高,且满足相同的训练效果,需要的迭代次数更少。
- 区别三:
- XGBoost与GDBT都是逐次迭代来提高模型性能,但是XGBoost在选取最佳切分点时可以开启多线程进行,大大提高了运行速度。
- 区别一:
-
XGBoost中封装的参数
主要由三种类型构成:
-
1 通用参数(general parameters):主要是宏观函数控制;
-
booster [缺省值=gbtree]
决定使用哪个booster,可以是gbtree,gblinear或者dart。
- gbtree和dart使用基于树的模型(dart 主要多了 Dropout),而gblinear 使用线性函数.
-
silent [缺省值=0]
- 设置为0打印运行信息;设置为1静默模式,不打印
-
nthread [缺省值=设置为最大可能的线程数]
- 并行运行xgboost的线程数,输入的参数应该<=系统的CPU核心数,若是没有设置算法会检测将其设置为CPU的全部核心数
-
-
2 Booster参数(booster parameters):取决于选择的Booster类型,用于控制每一步的booster(tree, regressiong);
- eta [缺省值=0.3,别名:learning_rate]
- 更新中减少的步长来防止过拟合。
- 在每次boosting之后,可以直接获得新的特征权值,这样可以使得boosting更加鲁棒。
- 范围: [0,1]
- gamma [缺省值=0,别名: min_split_loss](分裂最小loss)
- 在节点分裂时,只有分裂后损失函数的值下降了,才会分裂这个节点。
- Gamma指定了节点分裂所需的最小损失函数下降值。 这个参数的值越大,算法越保守。这个参数的值和损失函数息息相关,所以是需要调整的。
- 范围: [0,∞]
- max_depth [缺省值=6]
- 这个值为树的最大深度。 这个值也是用来避免过拟合的。max_depth越大,模型会学到更具体更局部的样本。设置为0代表没有限制
- 范围: [0,∞]
- min_child_weight [缺省值=1]
- 决定最小叶子节点样本权重和。XGBoost的这个参数是最小样本权重的和.
- 当它的值较大时,可以避免模型学习到局部的特殊样本。 但是如果这个值过高,会导致欠拟合。这个参数需要使用CV来调整。.
- 范围: [0,∞]
- subsample [缺省值=1]
- 这个参数控制对于每棵树,随机采样的比例。
- 减小这个参数的值,算法会更加保守,避免过拟合。但是,如果这个值设置得过小,它可能会导致欠拟合。
- 典型值:0.5-1,0.5代表平均采样,防止过拟合.
- 范围: (0,1]
- colsample_bytree [缺省值=1]
- 用来控制每棵随机采样的列数的占比(每一列是一个特征)。
- 典型值:0.5-1
- 范围: (0,1]
- colsample_bylevel [缺省值=1]
- 用来控制树的每一级的每一次分裂,对列数的采样的占比。
- 我个人一般不太用这个参数,因为subsample参数和colsample_bytree参数可以起到相同的作用。但是如果感兴趣,可以挖掘这个参数更多的用处。
- 范围: (0,1]
- lambda [缺省值=1,别名: reg_lambda]
- 权重的L2正则化项(和Ridge regression类似)。
- 这个参数是用来控制XGBoost的正则化部分的。虽然大部分数据科学家很少用到这个参数,但是这个参数
- 在减少过拟合上还是可以挖掘出更多用处的。.
- alpha [缺省值=0,别名: reg_alpha]
- 权重的L1正则化项。(和Lasso regression类似)。 可以应用在很高维度的情况下,使得算法的速度更快。
- scale_pos_weight[缺省值=1]
- 在各类别样本十分不平衡时,把这个参数设定为一个正值,可以使算法更快收敛。通常可以将其设置为负
- 样本的数目与正样本数目的比值。
- eta [缺省值=0.3,别名:learning_rate]
-
3 学习目标参数(task parameters):控制训练目标的表现。
-
objective [缺省值=reg:linear]
- “reg:linear” – 线性回归
- “reg:logistic” – 逻辑回归
- “binary:logistic” – 二分类逻辑回归,输出为概率
- “multi:softmax” – 使用softmax的多分类器,返回预测的类别(不是概率)。在这种情况下,你还需要多设一个参数:num_class(类别数目)
- “multi:softprob” – 和multi:softmax参数一样,但是返回的是每个数据属于各个类别的概率。
-
eval_metric [缺省值=通过目标函数选择]
可供选择的如下所示:
-
“rmse”: 均方根误差
-
“mae”: 平均绝对值误差
-
“logloss”: 负对数似然函数值
-
“
-
error”
- 二分类错误率。
- 其值通过错误分类数目与全部分类数目比值得到。对于预测,预测值大于0.5被认为是正类,其它归为负类。
-
“error@t”: 不同的划分阈值可以通过 ‘t’进行设置
-
“merror”: 多分类错误率,计算公式为(wrong cases)/(all cases)
-
“mlogloss”: 多分类log损失
-
“auc”: 曲线下的面积
-
-
seed [缺省值=0]
- 随机数的种子
-
-
4 案例分析
泰坦尼克号乘客存活分析
import pandas as pd
import numpy as np
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split
# 1、获取数据
titan = pd.read_csv("http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt")
# 2.数据基本处理
# 2.1 确定特征值,目标值
x = titan[["pclass", "age", "sex"]]
y = titan["survived"]
# 缺失值需要处理,将特征当中有类别的这些特征进行字典特征抽取
x['age'].fillna(x['age'].mean(), inplace=True)
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)
# 对于x转换成字典数据x.to_dict(orient="records")
# [{"pclass": "1st", "age": 29.00, "sex": "female"}, {}]
# 3.特征工程(字典特征抽取)
transfer = DictVectorizer(sparse=False)
x_train = transfer.fit_transform(x_train.to_dict(orient="records"))
x_test = transfer.fit_transform(x_test.to_dict(orient="records"))
# 4.xgboost模型训练和模型评估
# 模型初步训练
from xgboost import XGBClassifier
xg = XGBClassifier()
xg.fit(x_train, y_train)
print(xg.score(x_test, y_test))
# 针对max_depth进行模型调优
depth_range = range(10)
score = []
for i in depth_range:
xg = XGBClassifier(eta=1, gamma=0, max_depth=i)
xg.fit(x_train, y_train)
s = xg.score(x_test, y_test)
print(s)
score.append(s)
# 结果可视化
import matplotlib.pyplot as plt
plt.plot(depth_range, score)
plt.show()
1.12 lightGBM算法
1 定义
LightGBM提出的主要原因就是为了解决GBDT在海量数据遇到的问题,让GBDT可以更好更快地用于工业实践。
GBDT在每一次迭代的时候,都需要遍历整个训练数据多次。
如果把整个训练数据装进内存则会限制训练数据的大小;如果不装进内存,反复地读写训练数据又会消耗非常大的时间。
尤其面对工业级海量的数据,普通的GBDT算法是不能满足其需求的。
2 特点
在开源之后,就被别人冠以“速度惊人”、“支持分布式”、“代码清晰易懂”、“占用内存小”等属性。
LightGBM主打的高效并行训练让其性能超越现有其他boosting工具。在Higgs数据集上的试验表明,LightGBM比XGBoost快将近10倍,内存占用率大约为XGBoost的1/6。
LightGBM 主要基于以下方面优化,提升整体特特性:
- 基于Histogram(直方图)的决策树算法
- Lightgbm 的Histogram(直方图)做差加速
- 带深度限制的Leaf-wise的叶子生长策略
- 直接支持类别特征
- 直接支持高效并行
3 优化特点详解
-
基于Histogram(直方图)的决策树算法
直方图算法的基本思想是
- 先把连续的浮点特征值离散化成k个整数,同时构造一个宽度为k的直方图。
- 在遍历数据的时候,根据离散化后的值作为索引在直方图中累积统计量,当遍历一次数据后,直方图累积了需要的统计量,然后根据直方图的离散值,遍历寻找最优的分割点。
内存消耗的降低,计算上的代价也大幅降低
-
Lightgbm 的Histogram(直方图)做差加速
一个叶子的直方图可以由它的父亲节点的直方图与它兄弟的直方图做差得到。
通常构造直方图,需要遍历该叶子上的所有数据,但直方图做差仅需遍历直方图的k个桶。
利用这个方法,LightGBM可以在构造一个叶子的直方图后,可以用非常微小的代价得到它兄弟叶子的直方图,在速度上可以提升一倍。
-
带深度限制的Leaf-wise的叶子生长策略
Level-wise便利一次数据可以同时分裂同一层的叶子,容易进行多线程优化,也好控制模型复杂度,不容易过拟合。
- 但实际上Level-wise是一种低效的算法,因为它不加区分的对待同一层的叶子,带来了很多没必要的开销,因为实际上很多叶子的分裂增益较低,没必要进行搜索和分裂。
Leaf-wise则是一种更为高效的策略,每次从当前所有叶子中,找到分裂增益最大的一个叶子,然后分裂,如此循环。
- 因此同Level-wise相比,在分裂次数相同的情况下,Leaf-wise可以降低更多的误差,得到更好的精度。
- Leaf-wise的缺点是可能会长出比较深的决策树,产生过拟合。因此LightGBM在Leaf-wise之上增加了一个最大深度的限制,在保证高效率的同时防止过拟合。
-
直接支持类别特征
实际上大多数机器学习工具都无法直接支持类别特征,一般需要把类别特征,转化到多维的0/1特征,降低了空间和时间的效率。
而类别特征的使用是在实践中很常用的。基于这个考虑,LightGBM优化了对类别特征的支持,可以直接输入类别特征,不需要额外的0/1展开。并在决策树算法上增加了类别特征的决策规则。
在Expo数据集上的实验,相比0/1展开的方法,训练速度可以加速8倍,并且精度一致。目前来看,LightGBM是第一个直接支持类别特征的GBDT工具。
-
直接支持高效并行
LightGBM还具有支持高效并行的优点。LightGBM原生支持并行学习,目前支持特征并行和数据并行的两种。
- 特征并行的主要思想是在不同机器在不同的特征集合上分别寻找最优的分割点,然后在机器间同步最优的分割点。
- 数据并行则是让不同的机器先在本地构造直方图,然后进行全局的合并,最后在合并的直方图上面寻找最优分割点。
LightGBM针对这两种并行方法都做了优化:
- 在特征并行算法中,通过在本地保存全部数据避免对数据切分结果的通信;
- 在数据并行中使用分散规约 (Reduce scatter) 把直方图合并的任务分摊到不同的机器,降低通信和计算,并利用直方图做差,进一步减少了一半的通信量。
- **基于投票的数据并行(Voting Parallelization)**则进一步优化数据并行中的通信代价,使通信代价变成常数级别。在数据量很大的时候,使用投票并行可以得到非常好的加速效果。
4 API相关参数介绍
4.1 Control Parameters
| Control Parameters | 含义 | 用法 |
|---|---|---|
| max_depth | 树的最大深度 | 当模型过拟合时,可以考虑首先降低 max_depth |
| min_data_in_leaf | 叶子可能具有的最小记录数 | 默认20,过拟合时用 |
| feature_fraction | 例如 为0.8时,意味着在每次迭代中随机选择80%的参数来建树 | boosting 为 random forest 时用 |
| bagging_fraction | 每次迭代时用的数据比例 | 用于加快训练速度和减小过拟合 |
| early_stopping_round | 如果一次验证数据的一个度量在最近的early_stopping_round 回合中没有提高,模型将停止训练 | 加速分析,减少过多迭代 |
| lambda | 指定正则化 | 0~1 |
| min_gain_to_split | 描述分裂的最小 gain | 控制树的有用的分裂 |
| max_cat_group | 在 group 边界上找到分割点 | 当类别数量很多时,找分割点很容易过拟合时 |
| n_estimators | 最大迭代次数 | 最大迭代数不必设置过大,可以在进行一次迭代后,根据最佳迭代数设置 |
4.2 Core Parameters
| Core Parameters | 含义 | 用法 |
|---|---|---|
| Task | 数据的用途 | 选择 train 或者 predict |
| application | 模型的用途 | 选择 regression: 回归时, binary: 二分类时, multiclass: 多分类时 |
| boosting | 要用的算法 | gbdt, rf: random forest, dart: Dropouts meet Multiple Additive Regression Trees, goss: Gradient-based One-Side Sampling |
| num_boost_round | 迭代次数 | 通常 100+ |
| learning_rate | 学习率 | 常用 0.1, 0.001, 0.003… |
| num_leaves | 叶子数量 | 默认 31 |
| device | cpu 或者 gpu | |
| metric | mae: mean absolute error , mse: mean squared error , binary_logloss: loss for binary classification , multi_logloss: loss for multi classification |
4.3 IO parameter
| IO parameter | 含义 |
|---|---|
| max_bin | 表示 feature 将存入的 bin 的最大数量 |
| categorical_feature | 如果 categorical_features = 0,1,2, 则列 0,1,2是 categorical 变量 |
| ignore_column | 与 categorical_features 类似,只不过不是将特定的列视为categorical,而是完全忽略 |
| save_binary | 这个参数为 true 时,则数据集被保存为二进制文件,下次读数据时速度会变快 |
调参建议
| IO parameter | 含义 |
|---|---|
num_leaves | 取值应 <= 2^{(max_depth)}2(max_depth), 超过此值会导致过拟合 |
min_data_in_leaf | 将它设置为较大的值可以避免生长太深的树,但可能会导致 underfitting,在大型数据集时就设置为数百或数千 |
max_depth | 这个也是可以限制树的深度 |
下表对应了 Faster Speed ,better accuracy ,over-fitting 三种目的时,可以调的参数
| Faster Speed | better accuracy | over-fitting |
|---|---|---|
将 max_bin 设置小一些 | 用较大的 max_bin | max_bin 小一些 |
num_leaves 大一些 | num_leaves 小一些 | |
用 feature_fraction来做 sub-sampling | 用 feature_fraction | |
用 bagging_fraction 和 bagging_freq | 设定 bagging_fraction 和 bagging_freq | |
| training data 多一些 | training data 多一些 | |
用 save_binary来加速数据加载 | 直接用 categorical feature | 用 gmin_data_in_leaf 和 min_sum_hessian_in_leaf |
| 用 parallel learning | 用 dart | 用 lambda_l1, lambda_l2 ,min_gain_to_split 做正则化 |
num_iterations 大一些,learning_rate小一些 | 用 max_depth 控制树的深度 |
5 案例分析
鸢尾花数据集处理
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import mean_squared_error
import lightgbm as lgb
# 加载数据
iris = load_iris()
data = iris.data
target = iris.target
X_train, X_test, y_train, y_test = train_test_split(data, target, test_size=0.2)
# 模型训练
gbm = lgb.LGBMRegressor(objective='regression', learning_rate=0.05, n_estimators=20)
gbm.fit(X_train, y_train, eval_set=[(X_test, y_test)], eval_metric='l1', early_stopping_rounds=5)
print(gbm.score(X_test, y_test))
# 0.810605595102488
# 网格搜索,参数优化
estimator = lgb.LGBMRegressor(num_leaves=31)
param_grid = {
'learning_rate': [0.01, 0.1, 1],
'n_estimators': [20, 40]
}
gbm = GridSearchCV(estimator, param_grid, cv=4)
gbm.fit(X_train, y_train)
print('Best parameters found by grid search are:', gbm.best_params_)
# Best parameters found by grid search are: {'learning_rate': 0.1, 'n_estimators': 40}
# 模型调优
gbm = lgb.LGBMRegressor(num_leaves=31, learning_rate=0.1, n_estimators=40)
gbm.fit(X_train, y_train, eval_set=[(X_test, y_test)], eval_metric='l1', early_stopping_rounds=5)
print(gbm.score(X_test, y_test))
# 0.9536626296481988
2 机器学习算法实现
1.获取数据集
1.1 方法一:
from sklearn.datasets import load_iris
iris = load_iris()
1.2 方法二:
import pandas as pd
data = pd.read_csv("C:\\data\\FBlocaltion\\train.csv")
2.数据基本处理
# (备选):缺失值处理
data = data.replace(to_replace="?", value=np.NaN)
data = data.dropna()
# x_train,x_test,y_train,y_test为训练集特征值、测试集特征值、训练集目标值、测试集目标值
# x:数据集的特征值 y:数据集的标签值 test_size:测试集的大小,一般为float random_state 随机数种子,不同的种子会造成不同的随机采样结果。相同的种子采样结果相同。
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=22)
3.特征工程:标准化
# 通过一些转换函数将特征数据转换成更加适合算法模型的特征数据过程
# 方法一:( 标准化) <在已有样本足够多的情况下比较稳定,适合现代嘈杂大数据场景。>
from sklearn.preprocessing import StandardScaler
transfer = StandardScaler()
# 方法二:(归一化) <鲁棒性较差,只适合传统精确小数据场景。>
from sklearn.preprocessing import StandardScaler
transfer = MinMaxScaler()
# 方法三:(特征工程(字典特征抽取))
from sklearn.feature_extraction import DictVectorizer
transfer = DictVectorizer(sparse=False)
# 特征中出现类别符号,需要进行one-hot编码处理(DictVectorizer),x.to_dict(orient="records") 需要将数组特征转换成字典数据
x_train = transfer.fit_transform(x_train.to_dict(orient="records"))
x_test = transfer.fit_transform(x_test.to_dict(orient="records"))
# 对部分数据先拟合fit,找到该part的整体指标,如均值、方差、最大值最小值等等(根据具体转换的目的),然后对该trainData进行转换transform,从而实现数据的标准化。
x_train = transfer.fit_transform(x_train)
# 对剩余的数据(testData)使用同样的均值、方差、最大最小值等指标进行转换transform(testData),从而保证train、test处理方式相同。
x_test = transfer.transform(x_test)
4.机器学习(模型训练)
-
4.1 模型估计
# 方法一:(K-近邻算法) from sklearn.neighbors import KNeighborsClassifier # n_neighbors:查询默认使用的邻居数(默认= 5) # algorithm:{‘auto’,‘ball_tree’,‘kd_tree’,‘brute’} estimator = KNeighborsClassifier(n_neighbors=7,algorithm='auto') # 方法二:(线性回归) from sklearn.linear_model import LinearRegression estimator = LinearRegression() # 方法三:(逻辑回归) from sklearn.linear_model import LogisticRegression estimator = LogisticRegression() # 方法四:(决策树) from sklearn.tree import DecisionTreeClassifier, export_graphviz # criterion:特征选择标准("gini"或者"entropy"),前者代表基尼系数,后者代表信息增益。默认"gini",即CART算法。 # min_samples_split:内部节点再划分所需最小样本数(默认:2) # min_samples_leaf:叶子节点最少样本数(默认:1) # max_depth:决策树最大深度(10-100)# random_state:随机数种子 estimator = DecisionTreeClassifier(criterion="entropy", max_depth=5) -
4.2 模型调优
# 方法一:(网格搜索) # estimator:估计器对象 param_grid:估计器参数(dict){“n_neighbors”:[1,3,5]} cv:指定几折交叉验证 from sklearn.model_selection import GridSearchCV estimator = GridSearchCV(estimator, param_grid={"n_neighbors": [1, 3, 5]}, cv=3) # 方法二:(留出法) from sklearn.model_selection import train_test_split train_X , test_X, train_Y ,test_Y = train_test_split(X, Y, test_size=0.2,random_state=0) # 方法三:(留一法) from sklearn.model_selection import LeaveOneOut data = [1, 2, 3, 4] loo = LeaveOneOut() for train, test in loo.split(data): print("%s %s" % (train, test)) # 方法四:(K折交叉验证) from sklearn.model_selection import KFold folder = KFold(n_splits = 4, random_state=0, shuffle = False) # 方法五:(分层K折交叉验证) from sklearn.model_selection import StratifiedKFold sfolder = StratifiedKFold(n_splits = 4, random_state = 0, shuffle = False) # 方法六:(自助法) -
4.3 模型训练
estimator.fit(x_train, y_train)
5.模型评估
# 方法一:比对真实值和预测值
y_predict = estimator.predict(x_test)
print(">>>预测结果为:\n", y_predict)
print(">>>比对真实值和预测值:\n", y_predict == y_test)
# 方法二:回归系数(线性回归)
# 回归系数(regression coefficient):在回归方程中表示自变量x 对因变量y 影响大小的参数。回归系数越大表示x 对y 影响越大,正回归系数表示y 随x 增大而增大,负回归系数表示y 随x增大而减小。
print('回归系数:\n', estimator.coef_)
estimator.predict([[100, 80]]) # 平时成绩100, 期末成绩80的概率
# 方法二:直接计算准确率
score = estimator.score(x_test, y_test)
print(">>>准确率为:\n", score)
print(">>>预测最优得分:\n", estimator.best_score_)
print(">>>最优估计器:\n", estimator.best_estimator_)
print(">>>最优结果:\n", pd.DataFrame(estimator.cv_results_))
# 方法三:分类评估报告生成
from sklearn.metrics import classification_report
ret = classification_report(y_test, y_predict, labels=(2, 4), target_names=("良性", "恶性")
# 方法四:AUC指标评测
from sklearn.metrics import roc_auc_score
# 0.5~1之间,越接近于1约好
y_test = np.where(y_test > 2.5, 1, 0)
roc_auc_score(y_test, y_predict)