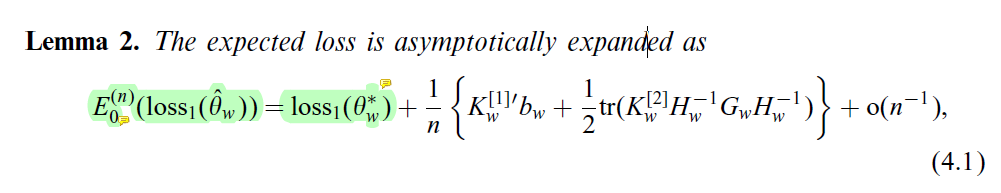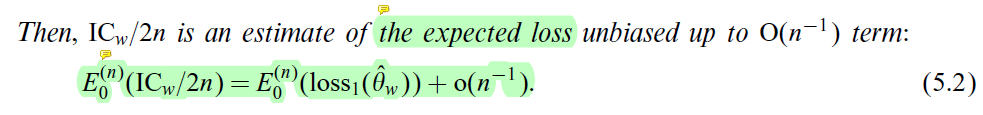基于样例的迁移学习——Covariate Shift——原始文章解读

Covariate Shift 是迁移学习下面的一个子研究领域, 对它的研究最早起源于统计学领域的一篇文章 “Improving predictive inference under covariate shift by weighting the log-likelihood function”. 本文将从机器学习的角度来解读这篇原始文章[1], 并着重提取那些比较适用于机器学习领域的要点. 因为Covariate Shift 目前还没有比较合适的中文翻译(有文献翻译成协方差转变, 但个人认为这不是很恰当), 故下文仍然使用这个英语表述.

1 Covariate Shift

Covariate Shift 定义：设源域(source domain)和目标域(target domain)的输入空间均为X, 输出空间均为Y. 源域的边际分布 $P_{S} (x)$ 与目标域的联合分布 $P_{T} (x)$ 不一致, 即 $P_{S}(x)\ne P_{T}(x)$ , 但两个域的条件分布一致, 即 $P_{S}(y|x)=P_{T}(y|x)$ .

2 文献[1]的动机

文献[1]的出现是为了解决错定模型(model misspecification)和Covariate Shift 共同发生的情形下使用极大似然估计(Maximum Likelihood Estimation, MLE)法估计参数所带来的问题.

在机器学习中, 一定是先假设数据是由潜在的模型产生, 这样学习才有意义. 从概率的视角, 我们会对条件分布P(y|x) 进行建模：(1)假设对x进行标记的概率模型P(y|x)来自某个模型空间 $F=\left\{ P(y|x;\theta)|\theta\in \Theta \right\}$ ; (2)利用数据集 $D=\left\{(x^{(i)},y^{(i)})\right\}_{i=1}^{m}$ 拟合出这个概率模型 $P(y|x;\hat{\theta} )$ , 作为对真实概率模型P(y|x) 的估计. 对于参数 $\theta$ 的学习是通过极大似然估计法: $\hat{\theta} =argmin_{\theta \in\Theta}\sum_{i=1}^{m}{logP(y^{(i)}|x^{(i)};\theta)}$ .

只要我们假定的模型空间F能够把真实的概率模型 $P_{S}(y|x)$ 包含在里面, 并且 $P_{S}(y|x)=P_{T}(y|x)$ , 那么这时候不管 $P_{S}(x), P_{T}(x)$ 是否相等, 我们都可以利用源域的标记数据 $D_{S}=\left\{(x^{(i)},y^{(i)})\right\}_{i=1}^{m_{s}}$ 拟合出源域真实模型 $P_{S}(y|x)$ 的估计模型 $P_{S}(y|x;\hat{\theta})$ , 再把 $P_{S}(y|x;\hat{\theta})$ 应用到目标域中去. 注意模型拟合时只需要源域的标记数据即可. To verify this argument, 下面对回归问题做个实验(实现细节见附录python程序): 设 $P(y|x)=P_{S}(y|x)=P_{T}(y|x), P_{S}(x)\ne P_{S}(x)$ $y|x\sim N(-x+x^{3},0.3^{2}) ...................(I)$

源域： $x\sim N(0.5,0.5^{2})...............(II)$ 目标域： $x\sim N(2.0,0.3^{2})...............(III)$

由(I)和(II)产生源域的一个包含1000个训练样例的集合 $D_{S}=\left\{(x^{(i)},y^{(i)})\right\}_{i=1}^{1000}$ (图1中蓝色的点), 我们希望利用这些数据, 学得一个模型, 使得该模型在目标域有尽可能小的测试误差. 由(I)和(III)产生目标域的一个包含100个测试样例的集合 $D_{T}=\left\{(x^{(i)},y^{(i)})\right\}_{i=1}^{100}$ (图1中红色的点), 用来测试所学模型在目标域的性能. 我们选用5个模型空间：第1个模型空间是1阶多项式空间 $F_{1}=\left\{P(y|x;\theta)|y|x\sim N(\theta_{0}+\theta_{1}x,\sigma^{2}))\right\}$ , 第2个模型空间是2阶多项式空间 $F_{2}=\left\{P(y|x;\theta)|y|x\sim N(\theta_{0}+\theta_{1}x++\theta_{2}x^2{},\sigma^{2}))\right\}$ , 依次类推. 后一个模型空间同时包含了前一个模型空间. 可见, 从第3阶开始以后的模型空间都包含了真实的模型, 而且从这3个模型空间拟合出来的模型对红色的点都拟合得很好, 即从 $F_{3},F_{4},F_{5}$ 这3个模型空间中分别挑出的3个模型, 在测试域都有比较低的测试误差. 而从 $F_{1},F_{2}$ 这2个模型空间中分别挑出的2个模型(绿色和红色的线条), 在测试域却表现得很差.

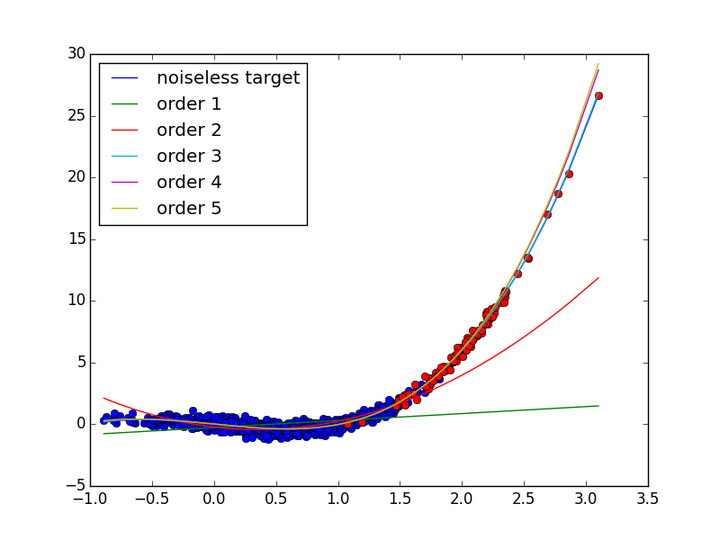
_ 图1 不同阶数多项式回归对比图

如果我们选择的模型空间F没能把潜在的真实的模型覆盖住, 那么我们实际上就是用了一个错定的模型(model misspecification), 这个时候, 如果 $P_{S}(x)\ne P_{S}(x)$ , 那么只用源域的标记数据, 利用普通的极大似然估计去学习一个模型, 那么这个模型在目标域的表现就会变得很差(设 $P_{S}(x), P_{S}(x)$ 的差异较大). 文献[1]正是考虑了错定模型和 $P_{S}(x)\ne P_{S}(x)$ 的情形下, 如何去改进我们的参数估计方法, 即改进极大似然估计.

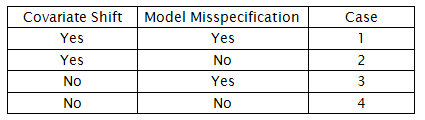
事实上, Covariate Shift 与错定模型这个两个事件的发生与否在很大程度上影响着我们对真实模型的学习. 具体地, 可以考虑表1中的4种情况：

_ 表1 Covariate Shift 与错定模型的所有可能组合

文献[1]要解决的是case 1 情形下的参数估计问题. 对于case 2和case 4, 由前面的论述和多项式回归的实验可以证明, 这2种情况下使用极大似然估计法去估计模型参数依然是没有问题的. Case 3只涉及到模型空间的选择问题, 这是关于先验知识或归纳偏好的问题, 文献[1]没有去讨论这种情况.

3 文献[1]的结果(主要贡献)

在case 1 发生的情形下, 已经不能直接使用极大似然估计法进行参数估计, 而应该使用加权的极大似然估计法. 具体地, 当我们选定模型空间F之后, 模型的参数应该这样估计:

$\hat{\theta}_{w} =argmin_{\theta \in \Theta}\sum_{i=1}^{m}{w(x^{(i)})logP(y^{(i)}|x^{(i)};\theta)} ............(IV)$

而且权重w(x)与模型空间F的选择可以通过一个准则——AIC信息准则的变种:

$IC_{w}=-2\sum_{i=1}^{m_{s}}{\frac{P_{T}(x^{(i)})}{P_{S}(x^{(i)})}logP(y^{(i)}|x^{(i)};\hat{\theta}_{w}) } + 2tr(\hat{J}_{w}\hat{H_{w}}^{-1} )...............(V)$

在选定了权重函数w(x)以及模型空间F之后, 只利用源域的标记数据, 就可以对(V)进行计算. 假设有若干个权重函数以及若干个模型空间, 我们最后选择那个 $IC_{w}$ 值最小的组合. 需要说明的是, 文献[1]中所考虑的w(x)的形式是 $w(x)=(\frac{P_{T}(x)}{P_{S}(x)})^\lambda, \lambda \in [0,1]$ ,对w(x)的选择实际上变成了对超参数 $\lambda$ 的选择. 而且文献[1]还做了一个在机器学习领域看起来不实际的假定: 假定 $P_{T}(x), P_{S}(x)$ 事先已知.

4 文献[1]的过程(文章脉络)

文献[1]的一条主体线索是:(1) $\rightarrow$ (2) $\rightarrow$ (3) $\rightarrow$ (4) $\rightarrow$ (5) $\rightarrow$ (6) $\rightarrow$ (7) $\rightarrow$ (8)

(1)学习场景设定: Covariate Shift和错定模型同时发生. $P_{T}(x),P_{S}(x)$ 事先已知.

_ $\downarrow$

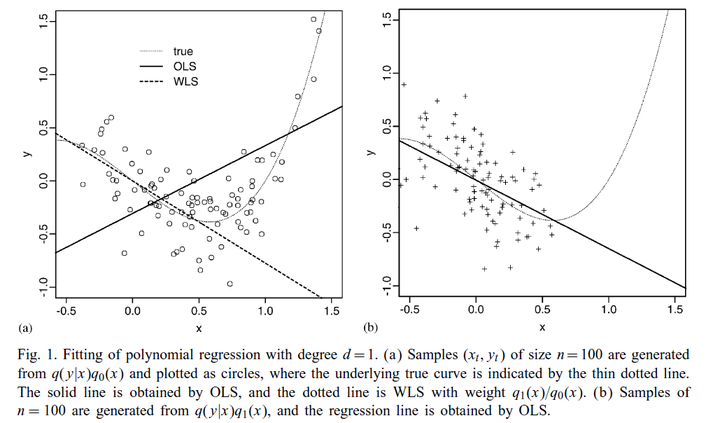
(2)用一个简单的线性回归例子, 说明使用极大似然估计法学习模型参数的危害

_ $\downarrow$

(3)借助importance sampling identity,大数定律说明学习模型的参数要使用加权极大似然估计法

考虑log损失, 由importance sampling identity：

$E_{(x,y)\sim P_{T}}(-logP(y|x;\theta))=-\int_{(x,y)}P_{T}(x,y)logP(y|x;\theta)dxdy\\=-\int_{(x,y)}P_{S}(x,y)\frac{P_{T}(x)}{P_{S}(x)} logP(y|x;\theta)dxdy\\=E_{(x,y)\sim P_{S}}(-\frac{P_{T}(x)}{P_{S}(x)} logP(y|x;\theta)) ......(VI)$

根据大数定律：

$\lim_{m_{s} \rightarrow \infty}{\frac{-1}{m_{s}} \sum_{i=1}^{m_{s}}{\frac{P_{T}(x^{(i)})}{P_{S}(x^{(i)})} logP(y^{(i)}|x^{(i)};\theta)}} = E_{(x,y)\sim P_{T}}(-logP(y|x;\theta)).............(VII)$

所以要学得一个在目标域期望损失小的模型, 需要在源域训练一个加权经验最小化的模型:

$\hat{\theta}_{w}=argmin_{\theta \in \Theta}\frac{-1}{m_{s}} \sum_{i=1}^{m_{s}}{\frac{P_{T}(x^{(i)})}{P_{S}(x^{(i)})} logP(y^{(i)}|x^{(i)};\theta)}.............(VIII)$

从(VI)到(VII)的过程中应用了大数定律, 这决定了(VIII)只能适用于 $m_{s}$ 取值很大的情形, 即我们拥有非常多的来自源域的标记数据. 否则, 如果 $m_{s}$ 不够大, 就要对权重进行选择, 即对 $w(x)=(\frac{P_{T}(x)}{P_{S}(x)})^\lambda, \lambda \in [0,1]$ 进行选择. 文献[1]从理论和实验两个角度详细探讨了w(x)的选取. 因为迁移学习通常假定我们能够很容易地获得大量来自源域的标记数据, 所以在迁移学习领域一般直接选择 $w(x)=\frac{P_{T}(x)}{P_{S}(x)}$ .

这一部分论述得比较详细, 因为机器学习领域的Covairate Shift 工作引用最多的就是这篇文献的这一部分的内容.

_ $\downarrow$

(4)考虑加权极大似然估计法所学模型的平均泛化误差, 通过平均泛化误差的展开式研究权重w(x)应该如何选取(肯定是选择w(x)使得模型的平均泛化误差最小)

_ $\downarrow$

(5) 由于(4)中的计算需要知道真实模型q(y|x)(4.1等式右端第一项的计算需要), 而真实模型q(y|x)是不知道的, 导致无法计算所学模型的平均泛化误差. 于是文献[1]推导出一个新的信息准则

该信息准则是模型平均泛化误差(4.1)的近似无偏估计, 可以作为选权重函数w(x)以及模型空间F的依据. 阐述了新提出的信息准则与AIC信息准则的联系.

_ $\downarrow$

(6)针对提出的信息准则 $IC_{w}$ ,做实验验证该信息准则的有效性.

_ $\downarrow$

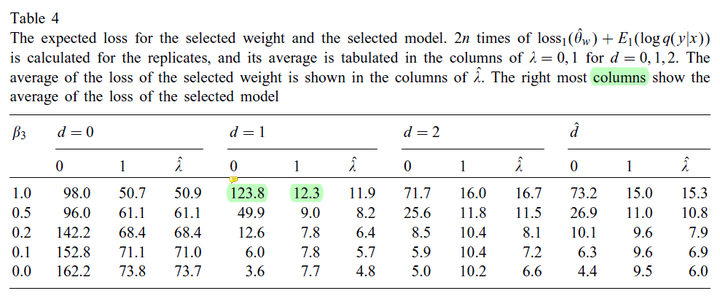
(7)实验验证当源域数据很多时, (5.1)可以近似代替(4.1), 即验证了

用实验进一步验证了信息准则 $IC_{w}$ 的有效性.

_ $\downarrow$

(8)说明了几点: 1, $P_{S}(x)$ 可以是事先已知, 也可以从数据中估计; 2, 权重函数w(x)的选取存在其他方式; 3, 说明加权极大似然估计也可以看成鲁棒回归.

参考文献

[1] H. Shimodaira, “Improving predictive inference under covariate shift by weighting the log-likelihood function” ,Journal of Statistical Planning and Inference, vol. 90, pp. 227–244, 2000.

附录

图1 不同阶数多项式回归对比图的python程序

import random
import numpy as np
import matplotlib.pyplot as plt
import numpy.linalg as linalg
from sklearn.linear_model import LinearRegression

print 'standard weights (w0,w1,w2,w3) = (0,-1,0,1)'

n = 1000

X_src = np.empty(n)
Y_src = np.empty(n)
X_tgt = np.empty(n / 10)
Y_tgt = np.empty(n / 10)

for i in range(n):
    X_src[i] = random.gauss(0.5,0.5)
    Y_src[i] = -X_src[i] + np.power(X_src[i],3) + random.gauss(0.0,0.3)
for i in range(n / 10):
    X_tgt[i] = random.gauss(2.0,0.3)
    Y_tgt[i] = -X_tgt[i] + np.power(X_tgt[i],3) + random.gauss(0.0,0.3)

reg = LinearRegression()
reg.fit([[v] for v in X_src],Y_src)
W1 = reg.intercept_,reg.coef_[0]

print 'W1 :',W1

reg = LinearRegression()
reg.fit([[v,v ** 2] for v in X_src],Y_src)
W2 = reg.intercept_,reg.coef_[0],reg.coef_[1]
print 'W2 :',W2

reg = LinearRegression()
reg.fit([[v,v ** 2,v ** 3] for v in X_src],Y_src)
W3 = reg.intercept_,reg.coef_[0],reg.coef_[1],reg.coef_[2]
print 'W3 :',W3

reg = LinearRegression()
reg.fit([[v,v ** 2,v ** 3,v **4] for v in X_src],Y_src)
W4 = reg.intercept_,reg.coef_[0],reg.coef_[1],reg.coef_[2],reg.coef_[3]
print 'W4 :',W4

reg = LinearRegression()
reg.fit([[v,v ** 2,v ** 3,v **4,v ** 5] for v in X_src],Y_src)
W5 = reg.intercept_,reg.coef_[0],reg.coef_[1],reg.coef_[2],reg.coef_[3],reg.coef_[4]
print 'W5 :',W5


X_plot = sorted(np.concatenate((X_src,X_tgt)))
plt.figure()
plt.plot(X_plot,[-i + np.power(i,3) for i in X_plot],label = 'noiseless target')
plt.plot(X_src,Y_src,'bo')
plt.plot(X_tgt,Y_tgt,'ro')

plt.plot(X_plot,[W1[0] + i * W1[1] for i in X_plot],label = 'order 1')
plt.plot(X_plot,[W2[0] + i * W2[1] + (i ** 2) * W2[2] for i in X_plot],label = 'order 2')
plt.plot(X_plot,[W3[0] + i * W3[1] + (i ** 2) * W3[2] + \
          (i ** 3) * W3[3] for i in X_plot],label = 'order 3')
plt.plot(X_plot,[W4[0] + i * W4[1] + (i ** 2) * W4[2] + \
          (i ** 3) * W4[3] + (i ** 4) * W4[4] for i in X_plot],label = 'order 4')
plt.plot(X_plot,[W5[0] + i * W5[1] + (i ** 2) * W5[2] + \
          (i ** 3) * W5[3] + (i ** 4) * W5[4] + \
          (i ** 5) * W5[5] for i in X_plot],label = 'order 5')

plt.legend(loc="best")
plt.show()

output:
standard weights (w0,w1,w2,w3) = (0,-1,0,1)
W1 : (-0.29578843795357851, 0.60680756922840728)
W2 : (-0.24137839883077888, -1.118596466841606, 1.6175250868307449)
W3 : (0.014386018101656139, -0.97736257687681483, -0.094743118854225233, 1.0393479036121429)
W4 : (0.015342798845553927, -0.98215866187620304, -0.097515221286365028, 1.0522118734968753, -0.0057473254710901367)
W5 : (0.01562503337882579, -0.97914406740220483, -0.10422149623464838, 1.0477376702208572, 0.005522699171098433, -0.003975707670178269)

编辑于 2017-04-17

基于样例的迁移学习——Covariate Shift——原始文章解读

悦读