实验一 :Apriori关联规则算法
一、实验目的
掌握有关Apriori关联规则算法的理论知识,从中了解关联规则的数学模型、基本思想、方法及应用。
二、实验任务
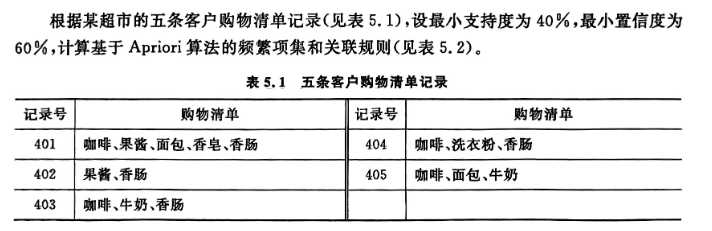
根据某超市的五条客户购物清单记录,使用Apriori关联规则算法进行计算,实例如下:
三、实验过程
1.关联规则概念介绍:
2.关联规则算法流程:
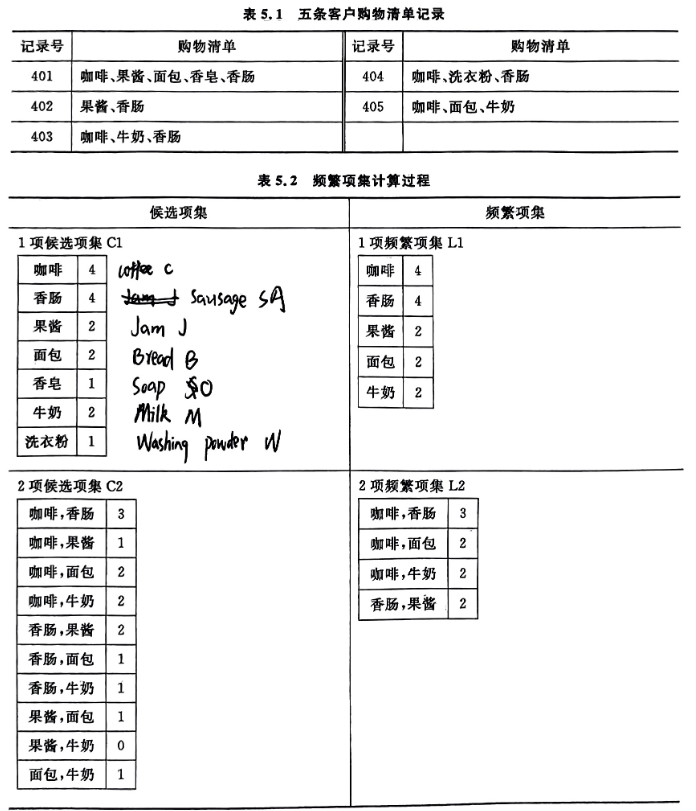
3.计算过程:
四、实验结果
实现平台:Matlab 2022A
实验代码:
% 清除命令窗口、工作区和所有图形
clear; clc; close all;
% 参数
goods = {'C,J,B,O,S'; 'J,S'; 'C,M,S'; 'C,W,S'; 'C,B,M'}; % 商品列表
min_sup = 0.4; % 最小支持度
%% Step 1: 寻找频繁1项集
% 1.获取所有项
all_items = []; % 存储所有的项
% (1)遍历每个交易记录,将商品拆分为单个项并去重
for i = 1:numel(goods)
items = strsplit(goods{i}, ',');
all_items = [all_items, items];
end
% (2)去重并排序
all_items = unique(all_items);
% % 测试
% disp('所有项:');
% disp(all_items);
% 2.计算每一项的支持度
support_data = struct(); % 存储支持度数据
for i = 1:numel(all_items)
item = all_items{i};
count = 0;
% 计算支持度
support = calculate_support(item, goods);
% 如果支持度满足阈值,则加入频繁1项集
if support >= min_sup
support_data.(item) = support;
end
end
% % 测试 显示频繁1项集和支持度
% disp('频繁1项集及其支持度:');
% disp(support_data);
%% 循环Step 2、Step 3: 寻找最终的频繁K项集
candidate_items = fieldnames(support_data); % 初始化候选项集
frequent_itemsets = fieldnames(support_data);% 初始化频繁项集
kk = 2; % 初始项集大小为2
while true
% Step 2: 生成候选K项
% k-1频繁项集 Lk_minus_1
Lk_minus_1 = frequent_itemsets(:,kk-1);
% 如果Lk_minus_1中的元素有逗号,则去掉
for i = 1:size(Lk_minus_1,1)
if ismember( ',', Lk_minus_1{i})
Lk_minus_1{i,1} = strrep(Lk_minus_1{i}, ',', '');
end
end
Ck = {}; % 用于存储预剪枝前的候选项集
% 1.排列组合
for i = 1:size(Lk_minus_1,1)
for j = i+1:size(Lk_minus_1,1)
set1 = Lk_minus_1(i);
set2 = Lk_minus_1(j);
% 检查 set2 是否为空
if isempty( set2{1,1} )
continue; % 如果为空,跳过当前循环迭代
end
% 对项集进行排序
combined_set = sort( cell2mat( {set1{1,1}, set2{1,1}} ) ); % 将单元格数组转换为字符数组
% 删除combined_set中重复的元素
combined_set = unique(combined_set, 'stable');
% 预剪枝第一部分,删除非k项集 若项集长度符合要求且不在候选项集中,则加入候选项集
if numel(combined_set) == kk && ~ismember(combined_set, Ck)
Ck{end+1,1} = combined_set;
end
end
end
% 2.预剪枝第二部分,经过“3.3.3 定理2”删除确定的非频繁k项集
Ck_pruned = {}; % 存储预剪枝后的候选项集
for i = 1:numel(Ck)
itemset = Ck{i};
% 生成项集的所有可能子集
subsets = nchoosek(itemset, numel(itemset) - 1);
%{
nchoosek 是 MATLAB 中的一个函数,用于生成指定集合中所有可能的 k 个元素的组合。
- 在这里,itemset 是一个项集,numel(itemset) - 1 表示生成的组合中包含的元素个数
- 比原始项集少一个,即生成项集的所有可能的大小为 k-1 的子集。
%}
% 检查项集的所有子集是否都在 Lk_minus_1 中
is_frequent = true;
for j = 1:size(subsets, 1)
temp = 0; % 临时标志
for ii = 1:length(Lk_minus_1)
% 检查 Lk_minus_1{ii} 是否为空
if isempty(Lk_minus_1{ii,1})
continue; % 如果为空,跳过当前循环迭代
end
if subsets(j,:) == Lk_minus_1{ii,1}
% 如果有任何一个子集不在 Lk_minus_1 中,则该项集不是频繁项集
temp = 1; % 说明在k-1频繁集
break;
end
end
if temp == 0
is_frequent = false; % 肯定不是频繁项集
break;
end
end
% 如果是频繁项集,则加入预剪枝后的候选项集
if is_frequent
Ck_pruned{end+1} = itemset;
end
end
% 3.填入候选项集
for i = 1:numel(Ck_pruned)
item_temp = Ck_pruned{i};
% item_temp可能为'DE'、'ADE',需变成'D,E'、'A,D,E'
% 如果项集中包含逗号,则表示已经是单个字符的单元格数组,不需要额外处理
if contains(item_temp, ',')
item_temp = item_temp;
else
% 将字符串拆分为单个字符,并使用逗号连接成字符串
item_temp = cellstr(strjoin(cellstr(item_temp'), ','));
end
candidate_items{i,kk } = item_temp{1,1};
end
% Step 3: 由候选K项目集生成频繁K项集
% 1.遍历每个候选项集,计算其支持度,判断是否为频繁项集
m = 0; % 行数标志
for i = 1:numel(Ck_pruned)
item_temp = Ck_pruned{i};
% item_temp可能为'DE'、'ADE',需变成'D,E'、'A,D,E'
% 如果项集中包含逗号,则表示已经是单个字符的单元格数组,不需要额外处理
if contains(item_temp, ',')
item_temp = item_temp;
else
% 将字符串拆分为单个字符,并使用逗号连接成字符串
item_temp = cellstr(strjoin(cellstr(item_temp'), ','));
end
% 计算支持度
support =calculate_support(item_temp{1,1}, goods);
% 如果支持度满足阈值,则将项集添加到频繁项集中
if support >= min_sup
m = m+1; % 行数索引
frequent_itemsets{m,kk} = item_temp{1,1};
end
end
% 如果没有满足最小支持度的项集,则跳出循环
if m == 0
break;
end
% 增加项集的大小
kk = kk + 1;
end
kk = kk-1; % kk不满足时跳出循环,实际的kk需要减1
%% 循环Step 4:获得的最终的频繁K项集,之后计算规则的置信度以及提升度。
all_confidence = {}; % 最终频繁k项集下的所有置信度
all_lift = {}; % 最终频繁k项集下的所有提升度
% 循环遍历最终的频繁K项集
for ii = 1:size(frequent_itemsets, 1)
% 检查 frequent_itemsets{ii,kk} 是否为空 注:行数size(frequent_itemsets,1)必然大于最终的频繁K项集的个数
if isempty( frequent_itemsets{ii,kk} )
continue; % 如果为空,跳过当前循环迭代
end
% 获取当前频繁项集
itemset = frequent_itemsets{ii,kk};
% 生成当前频繁项集的所有真子集
subsets = generate_subsets(itemset);
% 计算所有真子集的支持度
for i = 1:size( subsets,1 )
sup_temp = calculate_support(subsets{i,1}, goods);
subsets{i,2} = sup_temp;
end
% 计算所有子集subsets_add的支持度
subsets_add = subsets;
% itemset可能为'DE'、'ADE',需变成'D,E'、'A,D,E'
% 如果项集中包含逗号,则表示已经是单个字符的单元格数组,不需要额外处理
if contains(itemset, ',')
itemset = itemset;
else
% 将字符串拆分为单个字符,并使用逗号连接成字符串
itemset = cellstr(strjoin(cellstr(itemset'), ','));
end
subsets_add{ size( subsets,1 )+1,1 } = itemset;
subsets_add{ size( subsets,1 )+1,2 } = calculate_support(itemset, goods);
% 遍历当前频繁项集的所有真子集,计算置信度以及提升度。
curent_all_confidence = {}; % 当前频繁项集下的所有置信度
curent_all_lift = {}; % 当前频繁项集下的所有提升度
for i = 1:size( subsets,1 )
for j = 1:size( subsets,1 )
if i == j
continue; % 自己和自己无法关联,跳过当前循环迭代
end
% 计算置信度
% (1)置信度的分子
set1 = subsets{i,1};
set2 = subsets{j,1};
% 检查 set2 是否为空
if isempty( set2 )
continue; % 如果为空,跳过当前循环迭代
end
% 对项集进行排序
combined_set = sort([set1,',', set2]);
% 删除combined_set中重复的元素
combined_set = unique(combined_set, 'stable');
if combined_set(1) == ',' % 测试发现","在开头
combined_set = combined_set(2:end);
end
% combined_set可能为'DE'、'ADE',需变成'D,E'、'A,D,E'
% 如果项集中包含逗号,则表示已经是单个字符的单元格数组,不需要额外处理
if contains(combined_set, ',')
combined_set = combined_set;
else
% 将字符串拆分为单个字符,并使用逗号连接成字符串
combined_set = cellstr(strjoin(cellstr(combined_set'), ','));
end
% 在 subsets_add 中查找 combined_set 对应的行
index = find( strcmp( subsets_add(:, 1), combined_set{1,1} ) );
% 获取分子对应的支持度
confidence_numerator = subsets_add{index, 2};
% 获取分母对应的支持度
index = find( strcmp( subsets_add(:, 1), set1 ) );
confidence_denominator = subsets_add{index, 2};
% 计算置信度
confidence = confidence_numerator/confidence_denominator;
% 存储置信度
if i==1
curent_all_confidence{1,1} = [set1,'=>',set2];
curent_all_confidence{1,2} = confidence;
else
curent_all_confidence{size(curent_all_confidence,1)+1,1} = [set1,'=>',set2];
curent_all_confidence{size(curent_all_confidence,1),2} = confidence;
end
% 计算提升度
% 获取提升度的分母
index = find( strcmp( subsets_add(:, 1), set2 ) );
lift_denominator = subsets_add{index, 2};
% 计算提升度
lift = confidence/lift_denominator;% 计算提升度
% 存储提升度
if i==1
curent_all_lift{1,1} = [set1,'->',set2];
curent_all_lift{1,2} = lift;
else
curent_all_lift{size(curent_all_lift,1)+1,1} = [set1,'->',set2];
curent_all_lift{size(curent_all_lift,1),2} = lift;
end
end
end
% 存储置信度与提升度
if ii == 1
all_confidence{1,1} = itemset;
all_confidence{1,2} = curent_all_confidence;
else
all_confidence{size(all_confidence,1)+1,1} = itemset;
all_confidence{size(all_confidence,1),2} = curent_all_confidence;
end
if ii == 1
all_lift{1,1} = itemset;
all_lift{1,2} = curent_all_lift;
else
all_lift{size(all_lift,1)+1,1} = itemset;
all_lift{size(all_lift,1),2} = curent_all_lift;
end
end
% 生成当前频繁项集的所有真子集的函数
function subsets_fuc = generate_subsets(itemset)
subsets_fuc = {};
% 如果itemset中的元素有逗号,则去掉
if ismember( ',', itemset)
itemset = strrep(itemset, ',', '');
end
for i = 1:( length(itemset)-1 )
% 生成项集的所有可能子集
subsets_fuc_temp = nchoosek(itemset, numel(itemset) - i);
for j = 1:length(subsets_fuc_temp)
itemset_temp = subsets_fuc_temp(j,:); % 第j行
% subsets可能为'DE'、'ADE',需变成'D,E'、'A,D,E'
% 如果项集中包含逗号,则表示已经是单个字符的单元格数组,不需要额外处理
if contains(itemset_temp, ',')
itemset_cells = itemset_temp;
else
% 将字符串拆分为单个字符,并使用逗号连接成字符串
itemset_cells = cellstr(strjoin(cellstr(itemset_temp'), ','));
end
subsets_fuc = [subsets_fuc;itemset_cells];
end
end
% 按真子集的元素长度进行排序
[~, idx] = sort( cellfun(@numel, subsets_fuc) );
subsets_fuc = subsets_fuc(idx);
end
function support = calculate_support(itemset, transactions)
% 作用:计算支持度
% itemset:项集
% transactions:事务集
% 统计包含当前项集的交易记录数
count = 0;
for j = 1:numel(transactions)
% 将主字符串和子字符串分割成字符数组
str_chars = strsplit(transactions{j}, ',');
substr_chars = strsplit(itemset, ',');
% 检查子字符串中的所有字符是否都包含在主字符串中
if all(ismember(substr_chars, str_chars))
count = count + 1;
end
end
% 计算支持度
support = count / numel(transactions);
end
实验结果:
①基本结果
注:为方便输入输出,将原题中的中文购物清单替换成了英文字母,具体如下表
| 中文 | 咖啡 | 香肠 | 面包 | 香皂 | 牛奶 | 洗衣粉 | 果酱 |
|---|---|---|---|---|---|---|---|
| 英文字母 | C | S | B | O | M | W | J |
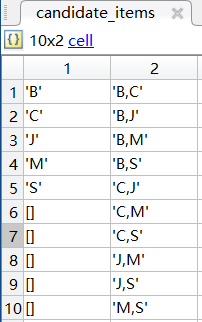
候选k项集candidate_items
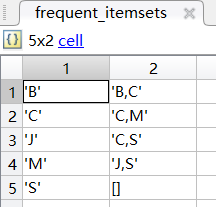
频繁k项集frequent_itemsets
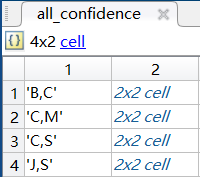
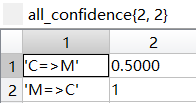
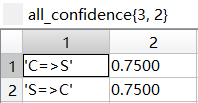
最终频繁k项集下的按照关联规则处理后的所有置信度all_confidence
 |  |
|---|---|
 | |
 | |
 |
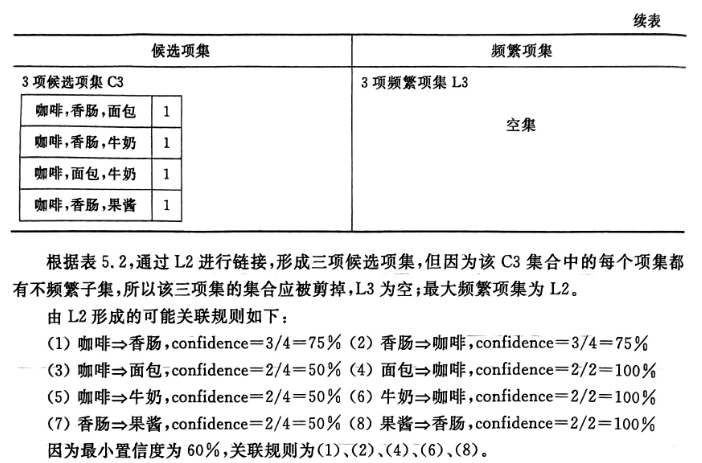
因为最小置信度为60%,所以最后的关联规则为:
咖啡→香肠,confidence=3/4=75%
香肠→咖啡,confidence=3/4=75%
面包→咖啡,confidence=2/2=100%
牛奶→咖啡,confidence=2/2=100%
果酱→香肠,confidence-2/2=100%
②额外结果
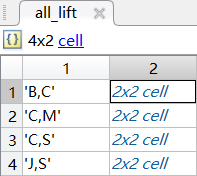
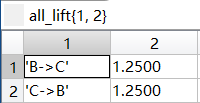
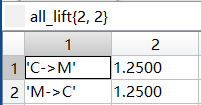
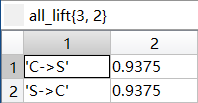
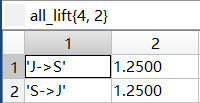
最终频繁k项集下的按照关联规则处理后的所有提升度all_lift
 |  |
|---|---|
 | |
 | |
 |