无人机辅助移动边缘计算的计算卸载优化:一种深度确定性策略梯度方法(5)——结果与分析
参考文献:
[1] Wang Y , Fang W , Ding Y , et al. Computation offloading optimization for UAV-assisted mobile edge computing: a deep deterministic policy gradient approach[J]. Wireless Networks, 2021:1-16.doi:https://doi.org/10.1007/s11276-021-02632-z
5 结果与分析
在本节中,我们通过数值模拟来说明提出的基于 DDPG 的无人机辅助 MEC 系统计算卸载框架。首先,介绍了仿真参数的设置。然后,对基于 DDPG 的框架在不同场景下的性能进行了验证,并与其他基线方案进行了比较。
5.1 仿真设置
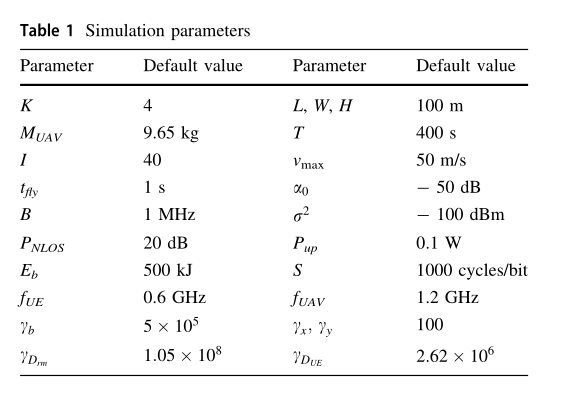
在无人机辅助的 MEC 系统中,我们考虑一个 K = 4 K=4 K=4 UEs 随机分布在 L × W = 100 × 100 m 2 L\times W = 100 \times 100 m^2 L×W=100×100m2 的2维平面,假设无人机在固定高度 H = 100 m H=100 m H=100m 飞行。根据[26]的定义,无人机的总质量为 M U A V = 9.65 k g M_{UAV}=9.65kg MUAV=9.65kg 。整个时间段 T = 400 s T=400s T=400s分为 I = 40 个时隙。参考[9],无人机最大飞行速度 v m a x = 50 m / s v_{max}=50 m/s vmax=50m/s,无人机在每个时隙的飞行时间 t f l y = 1 s t_{fly}=1s tfly=1s 。在参考距离为1米时,通道功率增益被设置为 α 0 = − 50 d B \alpha_0=-50 dB α0=−50dB 。设置传输带宽为 B = 1 M H z B=1MHz B=1MHz。假设没有信号遮挡下,接收机的噪声功率为 σ 2 = − 100 d B m \sigma^2=-100 dBm σ2=−100dBm 。如果信号在无人机与UE k之间传输过程中被阻塞,即信号为 f k ( i ) = 1 f_k(i)=1 fk(i)=1 。
渗透损失为 P N L O S = 20 d B P_{NLOS}=20 dB PNLOS=20dB 。我们假设 UEs 的传输功率为 P u p = 0.1 W P_{up}=0.1 W Pup=0.1W, UAV电池容量 E b = 500 k J E_b=500 kJ Eb=500kJ 和所需CPU周期/位 s=1000 周期/位。UE 和 MEC 服务器的计算能力分别设置为 f U E = 0.6 G H z f _{UE}=0.6 GHz fUE=0.6GHz 和 f U A V = 1.2 G H z f_{UAV}=1.2 GHz fUAV=1.2GHz。将所提出的状态归一化算法中的比例因子分别设置为 γ b = 5 × 1 0 5 , γ x = 100 , γ y = 100 , γ D r m = 1.05 × 1 0 8 , γ D U E = 2.62 × 1 0 6 \gamma_{b}=5 \times 10^{5}, \gamma_{x}=100, \gamma_{y}=100, \gamma_{D_{rm}}=1.05 \times 10^{8}, \gamma_{D_{UE}}=2.62 \times 10^{6} γb=5×105,γx=100,γy=100,γDrm=1.05×108,γDUE=2.62×106 。除另有说明外,具体仿真参数如表1所示。在我们的实验中,使用算法 3 在相同设置下多次运行获得的平均奖励来进行性能比较。
为作比较,现将四种基线方法说明如下:
- 将所有任务卸载到无人机(仅卸载):在每个时间段,无人机将在区域中心的固定位置向终端提供计算服务。UE 将所有的计算任务都交给无人机上的 MEC 服务器处理。
- 全本地执行(Local-only):在不借助无人机的情况下,终端的所有计算任务都在本地执行。
- 基于Actor Critical 的计算卸载算法 (AC):为了评价本文提出的基于 DDPG 的计算卸载算法的性能,在计算卸载问题上还实现了基于连续动作空间的 RL 算法 AC 。为了与 DDPG 进行比较, AC 还采用了状态归一化。
- 基于DQN的计算卸载算法(DQN):将传统的基于离散动作空间的 DQN 算法与提出的基于 DDPG 的算法进行比较。在无人机飞行过程中,角度水平被定义为 B = { 0 , π / 5 , … , 2 π } \mathcal{B}=\{0, \pi / 5, \ldots, 2 \pi\} B={0,π/5,…,2π} ,速度级别表示为 V = { 0 , v m a x / 10 , … , v m a x } \mathcal{V}=\{0, v_{max}/ 10, \ldots, v_{max}\} V={0,vmax/10,…,vmax} 和卸载比级别可设置为 O = { 0 , 0.1 , … , 1.0 } \mathcal{O}=\{0, 0.1, \ldots, 1.0\} O={0,0.1,…,1.0} 。为了与DDPG和AC进行比较,DQN还采用了状态归一化。
5.2 仿真结果与讨论
5.2.1 参数分析
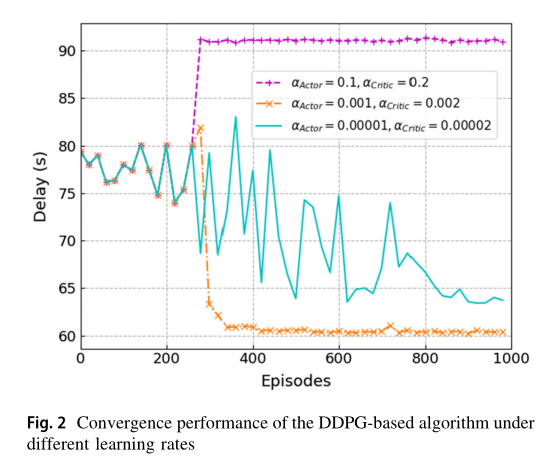
我们首先进行了一系列的实验,以确定最优值的重要超参数用于算法比较。本文算法在不同学习速率下的收敛性能如图 2 所示。我们假设评论网络和演员网络的学习速度是不同的。首先,我们可以清楚地看到,当 α Actor = 0.1 , α Critic = 0.2 \alpha_{\text {Actor }}=0.1, \alpha_{\text {Critic }}=0.2 αActor =0.1,αCritic =0.2 或 α Actor = 0.001 , α Critic = 0.002 \alpha_{\text {Actor }}=0.001, \alpha_{\text {Critic }}=0.002 αActor =0.001,αCritic =0.002 时,提出的算法可以收敛。但当 α Actor = 0.1 , α Critic = 0.2 \alpha_{\text {Actor }}=0.1, \alpha_{\text {Critic }}=0.2 αActor =0.1,αCritic =0.2 时,算法收敛到局部最优解。究其原因,大的学习率将使批评家网络和演员网络都有一个大的更新步骤。其次,我们可以发现当学习速率很小时,即 α Actor = 0.00001 , α Critic = 0.00002 \alpha_{\text {Actor }}=0.00001, \alpha_{\text {Critic }}=0.00002 αActor =0.00001,αCritic =0.00002 时,算法不能收敛。这是因为较低的学习率会导致dnn的更新速度较慢,需要更多的迭代片段来收敛。因此,actor网络和critic网络的最佳学习率分别为 α Actor = 0.001 , α Critic = 0.002 \alpha_{\text {Actor }}=0.001, \alpha_{\text {Critic }}=0.002 αActor =0.001,αCritic =0.002 。
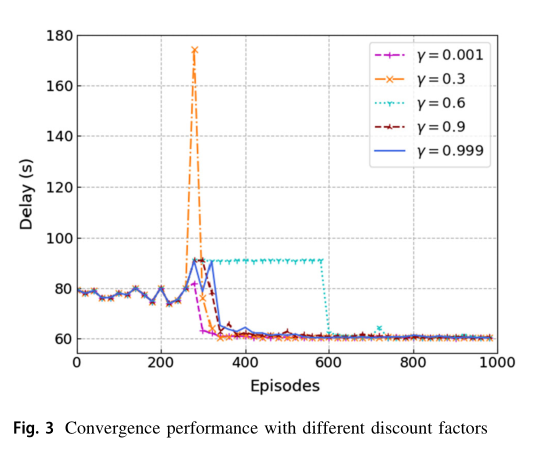
在图 3 中,我们比较了不同折扣因子 γ \gamma γ 对算法收敛性能的影响。结果表明,当折扣因子 γ = 0.001 \gamma=0.001 γ=0.001时,训练后的计算卸载策略性能最佳。原因是不同时期的环境差异很大,所以整个时间段的数据不能完全代表长期的行为。 γ \gamma γ 越大,说明 Q 表将整个时间段收集的数据视为长期数据,导致不同时间段的泛化能力较差。因此,适当的 γ \gamma γ 值将提高我们训练后的策略的最终性能,在接下来的实验中,我们将折扣因子 γ \gamma γ 设置为0.001。
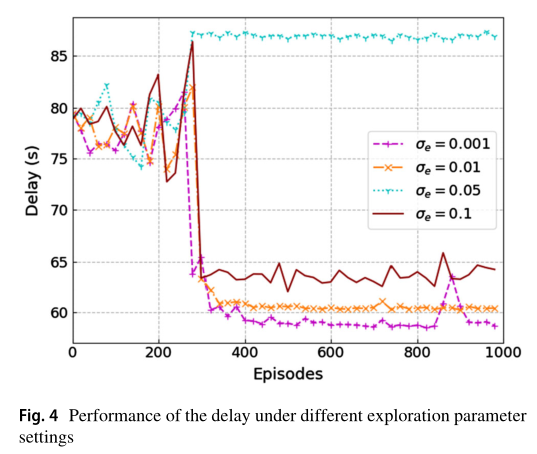
图 4 显示了在不同探测参数 σ e \sigma_e σe 下,本文算法在处理延迟方面的性能比较。该探测参数对算法的收敛性能影响很大。当算法收敛于 σ e = 0.1 \sigma_e=0.1 σe=0.1 时,最佳延迟在63秒上下波动。 σ e \sigma_e σe 值越大,随机噪声分布空间就越大,这使得 agent 可以探索更大的空间范围。当 σ e = 0.001 \sigma_e= 0.001 σe=0.001 时,算法在850次迭代时性能下降, σ e \sigma_e σe 较小,算法陷入局部最优解。因此,需要进行大量的实验才能获得无人机辅助场景下合适的探索设置。因此,为了在接下来的实验中获得更好的性能,我们选择 σ e = 0.01 \sigma_e=0.01 σe=0.01 。
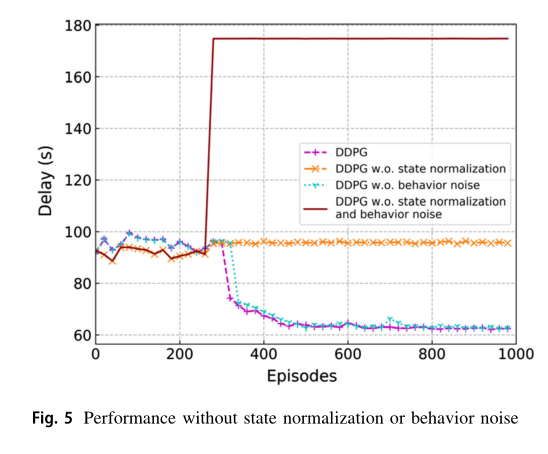
图 5 显示了不使用状态归一化和行为噪声的训练策略对 DDPG 训练算法的影响。一方面,如果在没有行为噪声的情况下训练 DDPG 算法,算法的收敛速度会变慢。另一方面,如果不进行状态归一化训练,即在状态归一化中不引入尺度因子,训练算法将失效。这是因为在没有状态归一化策略的情况下, E battery ( i ) E_{\text {battery }}(i) Ebattery (i)、 D remain ( i ) D_{\text {remain }}(i) Dremain (i) 和 D k ( i ) D_{k}(i) Dk(i) 的值都太大,导致 DNNs 的随机初始化输出更大的值。因此,如果在 DDPG 算法中不采用我们提出的状态归一化策略,该算法最终会变成贪婪算法。
5.2.2 性能比较
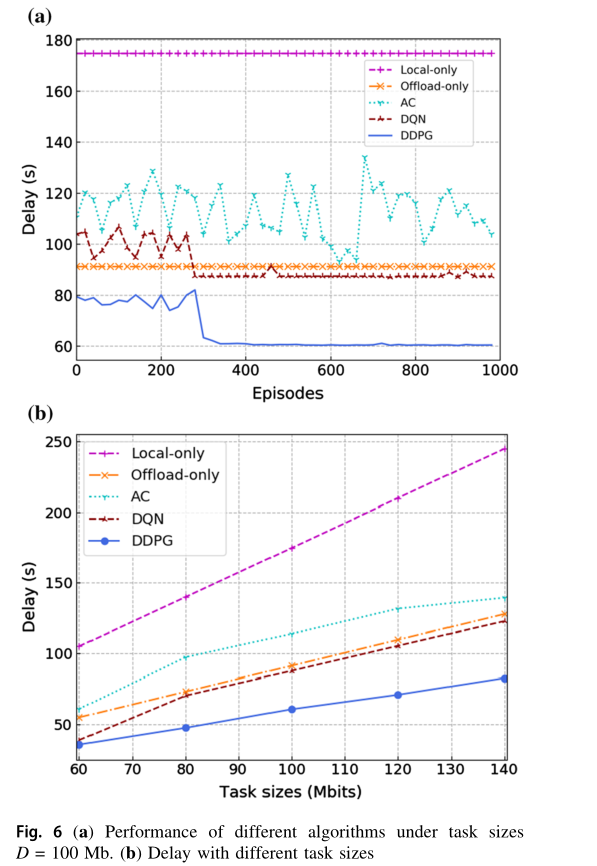
图 6 显示了不同算法之间的性能比较。在图 6a 中,我们对 R L算法的 DNNs 进行了总计1000次迭代的训练。从图中可以看出,随着迭代次数的增加, AC 算法不能收敛,而 DQN 和 DDPG 算法都可以收敛。这是因为 AC 算法存在着行动者网络和批评网络同时更新的问题。行动者网络的行为选择依赖于评论网络的价值功能,但评论网络本身难以收敛。因此,AC算法在某些情况下可能不收敛。相比之下, DQN 和 DDPG均受益于评价网络和目标网络的双网络结构,可用于切断训练数据之间的相关性,从而找到最优的行动策略。利用算法收敛后的延迟结果,比较不同任务大小设置下的算法,结果如图 6b 所示。在图 6b 中,对于相同的任务大小, DDPG 算法的时延在五种算法中始终是最低的。由于探索了离散的动作空间和可用动作之间的不可忽略空间, DQN 无法准确地找到最优卸载策略。而 DDPG 算法则探索一个连续的动作空间,并采取一个精确的动作,最终获得最优策略,显著减少了延迟。此外, DQN 算法的收敛速度远高于 DDPG 算法。 Offload-only 和 Local-only 两种算法不能充分利用整个系统的计算资源。因此,对于相同的任务大小, DDPG 算法的处理延迟明显低于 Offload-only 和 Local-only 算法。此外,随着任务大小的增大, DDPG 算法优化后的处理延迟增加速度明显慢于 Offload-only 和 Local-only 算法,表明了该算法的优势。
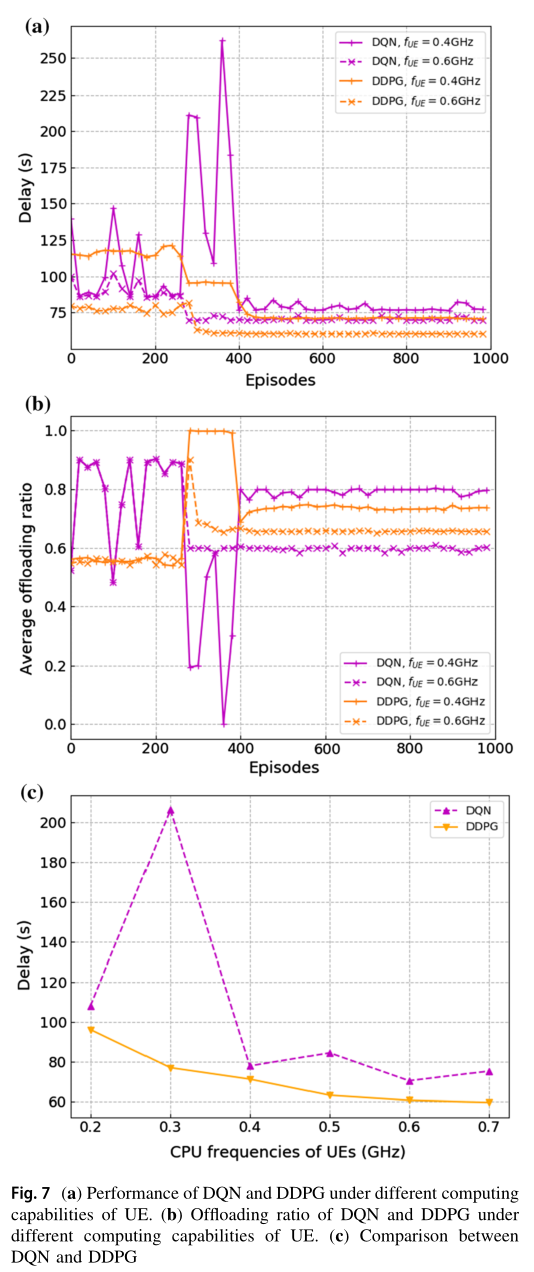
图 7a 和图 b 显示了同一组实验在延迟和卸载比方面的性能。图 7a 显示了不同 UE 计算能力下 DQN 方案和 DDPG 方案的收敛性能。本文提出的方案之所以没有与 AC 方案进行比较,是因为 AC 方案仍然不收敛。我们可以发现,当 UE 的计算能力较小时,即 f U E = 0.4 G H z f_{UE}=0.4 GHz fUE=0.4GHz 时,两种优化方案优化后的处理延迟要高于 f U E = 0.6 G H z f_{UE}=0.6 GHz fUE=0.6GHz 时的处理延迟。另一方面,从图 7b 中可以看出,当 UE 的计算能力较大时,系统的平均卸载率较小,因此 UE 更倾向于在本地执行任务。 UE 的计算能力越小,同时系统的数据处理速度越慢,导致本地执行和卸载之间的最大延迟越大。图 7c 为本文方案与 DQN 方案在不同 CPU 频率条件下优化后的时延比较。由图 7c 可以看出,在不同 UE 计算能力下,与 DQN 方案相比,本文提出的 DDPG 方案具有更低的延迟。这是因为 DDPG 方案可以输出多个连续的动作,而不是 DQN 中有限的离散动作集。因此, DDPG 可以找到一个精确的、对连续动作控制系统延迟影响较大的因子,即卸载比。
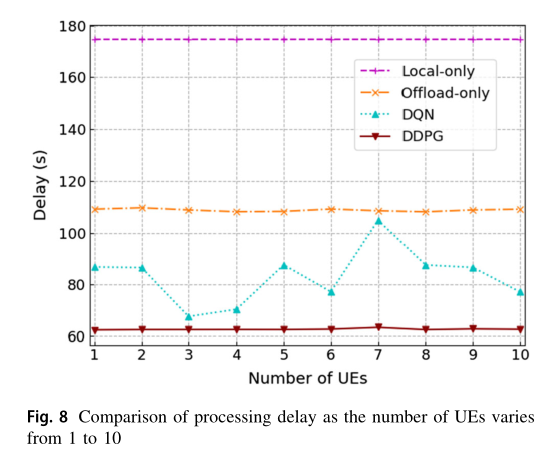
在图 8 中,我们比较了UE 的数量在1到10之间变化下 DDPG 方案、 DQN 、 Offload-only 和 Local-only 的平均处理延迟 。我们假设在不同数量的终端下,一个时间段内要完成的总任务大小是相同的。如图 8 所示,随着 UE 数量的增加,除 DQN 外,其他方案的平均处理延迟几乎不变。随着 UE 数量的增加, DQN 方案的处理延迟在 86 s左右波动。原因可以解释如下。不同数量 UE 的情况下, DQN 输出动作取值范围差异较大。因此,当样本作为 DNN 训练的输入时, DNN 可能倾向于输出更大的值。 DDPG 的演员网络输出多维动作,保证了 DNN 的输入数据在同一范围内,即 [0,1] ,保证了 DDPG 算法的收敛性和稳定性。此外,所提出的 DDPG 方案具有最小的延迟。这是因为 DDPG 方案能够在连续动作中找到最优值,从而得到最优控制策略。