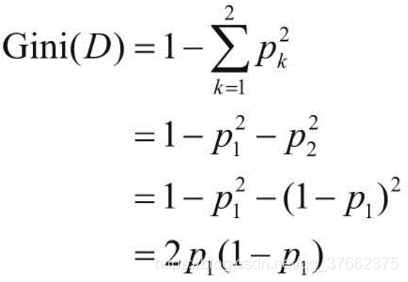摘要:
XGBoost作为一种高性能集成算法在Higgs机器学习挑战赛中大放异彩后,被业界所熟知,之后便在数据科学实际工程中被广泛应用。本文首先试从原理解析XGBoost分类器的具体构成并推导其理论公式以指导读者了解何种指标会影响XGBoost的性能表现。然后以一个高维网页广告数据集的分类任务入手,探讨XGBoost在数据集需要大量缺省值的处理、大量空白值的处理、正负样本比例失衡处理、离散型特征和连续性特征共存问题处理、数据特征维度较高情况处理条件下的表现,并针对XGBoost的不足之处提出一些解决方法和改进策略。
一、集成学习发展到XGBoost的提出
集成学习的基本思想是把多个学习器(专业点:叫基学习器:) )通过一定方法进行组合,以达到最终效果的提升。虽然每个学习器对全局数据的预测精度不高,但在某一方面的预测精度可能比较高,俗话说“三个臭皮匠顶个诸葛亮”,将多个学习器进行组合,通过优势互补即可达到强学习器的效果[1]。集成学习最早来自于 Valiant提出的PAC( Probably Approximately Correct)学习模型[2],该模型首次定义了弱学习和强学习的概念:识别准确率仅比随机猜测高一些的学习算法为弱学习算法;识别准确率很高并能在多项式时间内完成的学习算法称为强学习算法。该模型提岀给定仼意的弱茡习算法,能否将其提升为强学习算法的问题。[3]1990年, Schapire对其进行了肯定的证明。这样一来,我们只需要先找到—个弱学习算法,再将其提升为强学习算法,而不用开始就找强学习算法,因为强学习算法比弱学习算法更难找到[4]。目前集成学习中最具代表性的方法是: Boosting、 Bagging和 Stacking[5]。
1.Boosting
简单来讲, Boosting会训练一系列的弱学习器,并将所有学习器的预测结果组合起来作为最终预测结果,在学习过程中,后期的学习器更关注先前学习器学习中的错误。1995年, Freund等人提出了AdaBoost,成为了 Boosting代表性的算法。[6]Adaboost继承了 Boosting的思想,并为每个弱学习器赋予不同的权值,将所有弱学习器的权重和作为预测的结果,达到强学习器的效果。Gradient Boosting是Boosting思想的另外一种实现方法,由 Friedman于1999年提出。与AdaBoost类似, Gradient Boosting也是将弱学习器通过一定方法的融合,提升为强学习器。[7]与 Adaboost不同的是,它将损失函数梯度下降的方向作为优化的目标,新的学习器建立在之前学习器损失函数梯度下降的方向,代表算法有GBDT、 XGBoost( XGBoost会在1.2.2节详细介绍)等。一般认为, Boosting可以有效提高模型的准确性,但各个学习器之间只能串行生成,时间开销较大[8]。
2.Bagging
Bagging( Bootstrap Aggregating)对数据集进行有放回采样,得到多个数据集的随机采样子集,用这些随机子集分别对多个学习器进行训练(对于分类任务,采用简单投票法;对于回归任务采用简单平均法),从而得到最终预测结果。随机森林是 Bagging最具代表性的应用,将 Bagging的思想应用于决策树,并进行了一定的扩展。一般情况下, Bagging模型的精度要比 Boosting低,但其各学习器可并行进行训练,节省大量时间开销[9]。
3.Stacking
Stacking的思想是通过训陈练集训练好所有的基模型,然后用基模型的预测结果生成一个新的数据,作为组合器模型的输入,用以训练组合器模型,最终得到预测结果。(见机器学习笔记(7))组合器模型通常采用逻辑回归。
4.XGBoost的诞生
XGBoost(Extreme Gradient Boosting)由华盛顿大学的陈天奇博士提出,最开始作为分布式(深度)机器学习研究社区(DMLC)小组的研究项目之一[10]。后因在希格斯(Higgs)机器学习挑战赛中大放异彩,被业界所熟知,在数据科学应用中广泛应用。目前,一些主流的互联网公司如腾讯、阿里巴巴等都已将XGBoost应用到其业务中,在各种数据科学竞赛中,XGBoost也成为竞赛者们夺冠的利器。XGBoost在推荐、搜索排序、用户行为预测、点击率预测、产品分类等问题取得了良好的效果。虽然这些年神经网络(尤其是深度神经网络)变得越来越流行,但XGBoost仍旧在训练样本有限、训练时间短、调参知识缺乏的场景下具有独特的优势[11]。相比深度神经网络,XGBoost能够更好地处理表格数据并具有更强的可解释性,另外具有易于调参、输入数据不变性等优势。
5.XGBoost的优势
XGBoost是GradientBoosting的实现,相比其他实现方法,XGBoost做了很多优化,在模型训练速度和精度上都有明显提升,其优良特性如下。
1)将正则项加入目标函数中,控制模型的复杂度,防止过拟合。
2)对目标函数进行二阶泰勒展开,同时用到了一阶导数和二阶导数
3)实现了可并行的近似直方图算法。
4)实现了缩减和列采样(借鉴了GBDT和随机森林)。
5) 实现了快速直方图算法,引入了基于loss-guide的树构建方法(借鉴了LightGBM)。
6)实现了求解带权值的分位数近似算法(weighted quantile sketch)。
7)可根据样本自动学习缺失值的分裂方向,进行缺失值处理。
8)数据预先排序,并以块(block)的形式保存,有利于并行计算。
9)采用缓存感知访问、外存块计算等方式提高数据访问和计算效率。
10)基于Rabit实现分布式计算,并集成于主流大数据平台中。
11)除CART作为基分类器外,还支持线性分类器及LambdaMART排序模型等算法。
12)实现了DART,引入Dropout技术[12-14]。
二、XGBoost简单推导
XGBoost模型通过CART实现集成学习,通过Gradient Booosting进行模型的训练,下面将从这两方面对XGBoost进行推导。
1.CART算法
1.1 GART简介
XGBoost由多棵CART( Classification And Regression Tree)组成,每一棵决策树学习的是目标值与之前所有树预测值之和的残差,多棵决策树共同决策,最后将所有树的结果累加起来作为最终的预测结果。在训练阶段,每棵新增加的树是在已训练完成的树的基础上进行训练的。CART于1984年由 Breiman等人提出,在数据分析和机器学习领域很受欢迎,并在近几十年中一直保持着强大的生命力[15-17]。CART算法的实现原理和ID3、C45的实现原理类似,相信读者理解了ID3、C45算法后,学习CART算法也会易如反掌。CART算法的决策树类型:分类树和回归树。分类树的预测值是离散的,通常会将叶子节点中多数样本的类别作为该节点的预测类别。回归树的预测值是连续的,通常会将叶子节点中多数样本的平均值作为该节点的预测值。CART算法采用的是二分递归分裂的思想:首先按一定的度量方法选出最优特征及切分点,然后通过该特征及切分点将样本集划分为两个子样本集,即由该节点生成两个子节点,依次递归该过程直到满足结束条件。因此,CART算法生成的决策树均为二叉树。通常CART算法在生成决策树后,采用剪枝算法对生成的决策树进行剪枝,防止对噪声数据或者一些孤立点的过度学习导致过拟合。
1.2 CART的生成
在特征选择方法上,ID3算法采用信息增益来度量划分数据集前后不确定性減少的程度,从而进行最优特征选择,C4.5算法采用的是信息增益比。CART算法则采用了一种新的策略:分类树采用基尼指数最小化进行特征选择,回归树则采用平方误差最小化分类树的生成CART生成树的过程是自上而下进行的,从根节点开始,通过特征选择进行分裂。CART采用基尼指数作为特征选择的度量方式生成分类树,通过基尼指数最小化进行最优特征选择,决定最优切分点。基尼指数的定义如下[18]:
式子中,D为样本集,K代表类别个数;Pk表示类别为k的样本所占有样本的比值。由此可知,样本分布越集中,则基尼指数越小。当所有样本都是一个类别是,基尼指数为0;样本分布越均匀,则基尼指数越大。对于二分类问题可进行如下推导:
基尼指数越大,表明经过A特征分裂后的样本不确定性越大,反之,不确定性越小。针对所有可能的特征及所有可能的切分点,分别计算分裂后的基尼指数,选择基尼指数最小的特征及切分点作为最优特征和最优切分点。通过最优特征和最优切分点对节点进行分裂,生成子节点,即将原样本集划分成了两个子样本集,然后对子节点递归调用上述步骤,直到满足停止条件。一般来说,停止条件是基尼指数小于某阈值或者节点样本数小于一定阈值。当然,如果某节点的样本已全部属于一种类别,分裂也会停止。由此,我们可以得出分类树生成的步骤。
1)从根节点开始分裂。
2)节点分裂之前,计算所有可能的特征及它们所有可能的切分点分裂后的基尼指数
3)选出基尼指数最小的特征及其切分点作为最优特征和最优切分点。通过最优特征和最优分点对节点进行分裂,生成两个子节点。
4)对新生成的子节点递归步骤2、3,直至满足停止条件[19]
5)生成分类树。
2.Boosting思想
Boosting的基本思想是将多个弱学习器通过一定的方法整合为一个强学习器。代表性的两种实现方式是AdaBoost和Gradient Boosting。这里我们只介绍Gradient Boosting。
Gradient Boosting与Adaboost不同的是,它将损失函数梯度下降方向作为优化目标。因为损失函数用于衡量模型对数据的拟合程度,损失函数越小,说明模型对数据拟合得越好,在梯度下降的方向不断优化,使损失函数持续下降,从而提高了模型的拟合程度。
Gradient Boosting既可以应用于分类问题,也可以应用于回归问题。下面以回归问题为例介绍Gradient Boosting的训练过程。假设模型为F(x),损失函数为L(y,F(X))=(y-F(x))2/2,每轮模型训练的目标是使预测值与真实值的平方误差最小。Gradient Boosting算法表示如下:
三、广告分类任务
本节将以一个互联网广告数据集为例,介绍如何通过使用XGBoost实现广告分类器,以区分网页上的图片是广告还是正常网页内容,并利用PCA对训练集和测试集的集合数据进行降维(降至二维或者三维),然后对降维后的任务进行可视化,观察训练集和测试集数据分布是否有明显的差,以优化XGBoost处理高维数据的能力。
数据集[20]是UCI发布的一个互联网广告数据集,总共包含3279张图片,其中2820张为正常网页,459张为广告。每个样本包含1558个特征,其中包含3个连续特征,分别是height、weight和ratio,其余均为二值特征。另外,样本还有一个字段用于标明样本是否为广告(ad-广告,nonad-非广告)[21]。
对该数据集进行分类主要存在的问题是:
(1)大量缺省值的处理
(2)大量空白值的处理
(3)正负样本比例失衡
(4)离散型特征和连续性特征共存
(5)数据特征维度较高
因此在使用XGBoost进行分类的过程中会存在很多待处理问题,下一部分我们会针对这些问题一一解决[22-23]。
四、XGBoost分类器的构建
1.数据分析
1.1 数据的读取与预处理
首先读取数据集的,因为数据文件并不包含表头,因此将header设置为None,此处通过设置参数error_bad_lines忽略无效数据,代码如下:
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_auc_score
import matplotlib.pyplot as plt
import seaborn as sns
from bayes_opt import BayesianOptimization
data = pd.read_csv('../input/ad-dataset/ad.data', header = None, error_bad_lines = False)数据集中缺失值用“?”表示,此处将其替换为np.nan,处理代码如下:
data = data.replace('[?]', np.nan, regex=True)数据缺失是数据分析中经常遇到的问题之一。当比例缺失很小时。可直接对缺失记录进行舍弃或手工处理。当缺失值占有一定比例时。可以采取特殊值填充、平均值填充等方法进行填充。因为XGBoost本身就实现了对缺失值的处理算法,此处缺失值不在进行填充处理。
目前数据集label字段取值为ad.和nonad.,分别代表样本为广告和非广告,将其转化为1和0表示,代码如下:
data.label = data.label.replace(['ad.', 'nonad.'], [1,0])
将数据集划分为训练集和测试集,次数采用4:1的划分比例:
mask = np.random.rand(len(data)) < 0.8
train = data[mask]
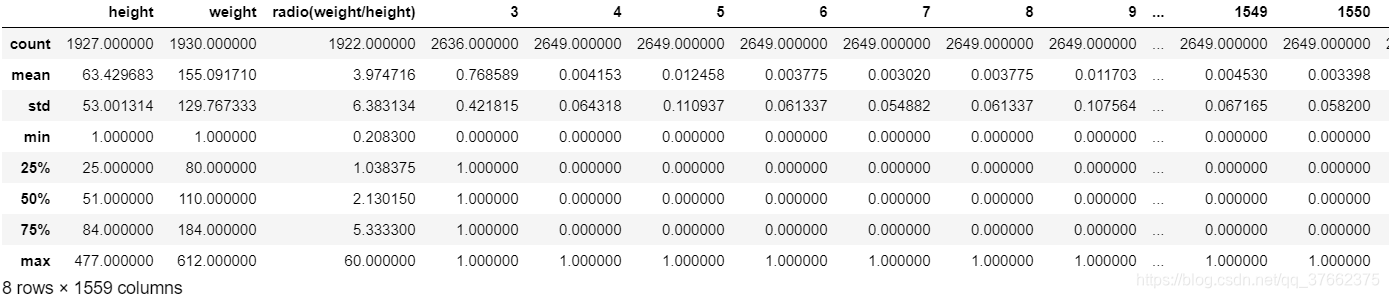
test = data[~mask]为了更准确的理解数据,我们通过train.describe()对特征进行简单的统计计算。describe方法可计算数值特征的计数、平均数、标准差、最小值、最大值以及25、50、75的百分位数。describe的输出如下:
表1:describe的输出
1.2目标特征
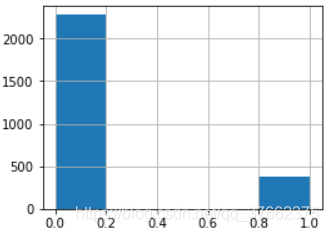
下面看一下label特征的取值分布,因为该问题为二分类问题,因此label取值只有两个,绘制如下:
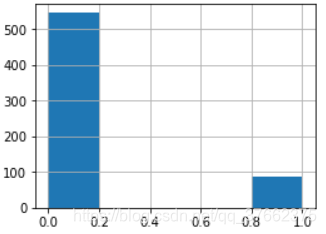
图1:label特征的取之分布:左侧为训练集,右侧为测试集
可以看到训练集的正样本与负样本的比例大概是1:7,测试集大概为1:5,正负样本不均衡,后续需要考虑平衡正负样本。
1.3连续性特征
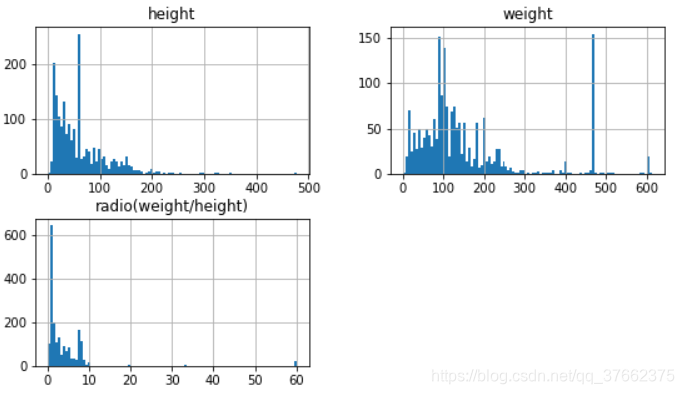
分析完目标特征后,下面对数据集的其他特征进行分析。此数据集包含3个连续型特征,对其处理并绘制数据分布直方图,方便直观地分析每个特征的分布情况:
cont_feas = ['height', 'weight', 'radio(weight/height)']
train[cont_feas].hist(bins = 100, figsize = (9,5))
plt.show()图2:训练集三个连续型特征分布情况
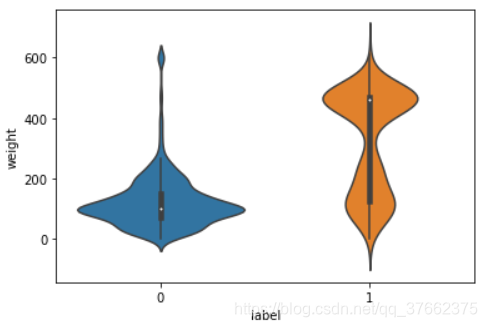
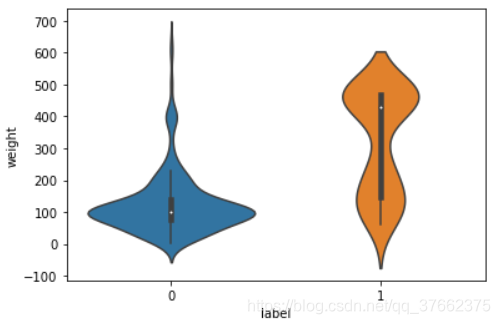
可以看到,分布图中有些特征并未遵守任何可解释的概率分布函数,可以尝试转化一些特征时期更接近于高斯分布,但这种方法不一定奏效。另外,还可以对连续特征在正负样本的不同分布上进行对比,这里通过seaborn库中的violinplot函数绘制小提琴图来完成:
sns.violinplot(x = 'label', y = 'weight', data = train)
sns.violinplot(x = 'label', y = 'weight', data = test)
plt.show()
图3:特征width在训练集(左)和测试集(右)的正负样本上的分布
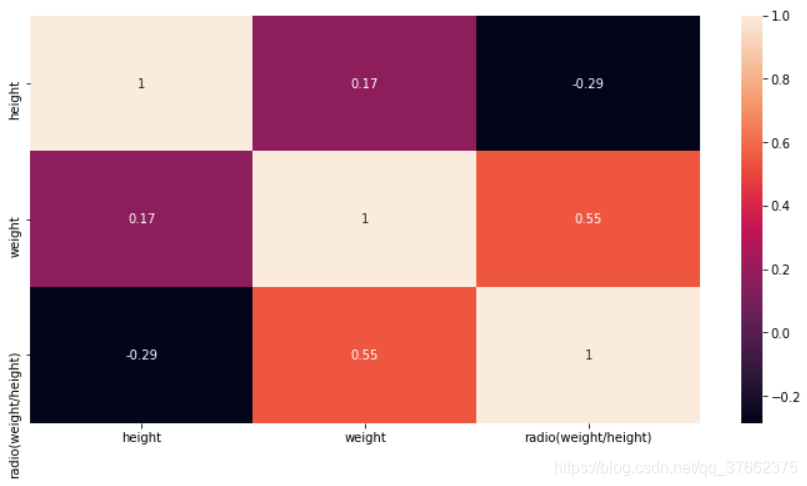
1.4皮尔逊(pearson)相关系数
皮尔逊相关系数可以用来度量两个特征之间的相关性[24],为协方差和标准差的商,取值为(-1~1),可通过seaborn库的heatmap来绘制皮尔逊系数的热点图:
plt.subplots(figsize = (12, 6))
corr_mat = train[cont_feas].corr()
sns.heatmap(corr_mat, annot = True)
plt.show()图4:特征之间的皮尔逊相关系数
2.通过PCA降维
我们通过PCA对训练集和测试集的集合数据进行降维(二维)[25],然后对降维后的数据进行可视化,观察是否具有明显区别。代码如下
from sklearn.decomposition import PCA
all_data = all_data.iloc[np.random.permutation(len((all_data)))]
#PCA
X = all_data.iloc[:, :1557]
Y = all_data.iloc[:, 1557:]
pca = PCA(n_components = 2)
X_pca = pca.fit_transform(X)
#得到正负样本集
label = all_data.label
pos_mask = label >= 0.5
neg_mask = label < 0.5
pos = X_pca[pos_mask]
neg = X_pca[neg_mask]
# 可视化
plt.scatter(pos[:, 0], pos[:, 1], s= 60 ,marker = 'o', c = 'r')
plt.scatter(neg[:, 0], neg[:, 1], s= 60 ,marker = '^', c = 'b')
plt.show()图中圆形代表训练集,三角型代表测试集,可以看到训练集与测试集分布相似。
图5:PCA降维
3.训练
3.1训练参数定义
# 训练参数定义
testparams = {
"objective":"binary:logistic",
"biister":"gbtree",
"eta":"0.1",
"eval_metric":"auc",
"scale_pos_weight":neg_num/pos_num,
"max_depth":6
}
num_round = 503.2模型训练
# 开始训练
import xgboost as xgb
xgb_train = xgb.DMatrix(train.iloc[:, :1557], train['label'])
xgb_test = xgb.DMatrix(test.iloc[:, :1557], test['label'])
watchlist = [(xgb_train, 'train'), (xgb_test, 'test')]
model = xgb.train(testparams, xgb_train, num_round, watchlist)模型训练的结果为:
[0] train-auc:0.94726 test-auc:0.90946
[1] train-auc:0.95288 test-auc:0.91268
[2] train-auc:0.95283 test-auc:0.91285
[3] train-auc:0.95304 test-auc:0.91285
[4] train-auc:0.95316 test-auc:0.91285
……
[43] train-auc:0.99671 test-auc:0.97571
[44] train-auc:0.99746 test-auc:0.97396
[45] train-auc:0.99761 test-auc:0.97267
[46] train-auc:0.99766 test-auc:0.97286
[47] train-auc:0.99777 test-auc:0.97463
[48] train-auc:0.99782 test-auc:0.97381
[49] train-auc:0.99781 test-auc:0.9725五、结论
本文尝试了从原理解析XGBoost分类器的具体构成,然后以一个高维网页广告数据集的分类任务入手,探讨了XGBoost在数据集需要大量缺省值的处理、大量空白值的处理、正负样本比例失衡处理、离散型特征和连续性特征共存问题处理、数据特征维度较高情况处理条件下的表现。实验数据标明在使用PCA进行数据降维处理后再使用XGBoost来完成高维数据的分类任务,可显著减少训练时间,但准确率会有一定程度的下降。
参考文献
[1] R. Bekkerman. The present and the future of the kdd cup competition: an outsider’s perspective.
[2] R. Bekkerman, M. Bilenko, and J. Langford. Scaling Up Machine Learning: Parallel and Distributed Approaches. Cambridge University Press, New York, NY, USA, 2011.
[3] J. Bennett and S. Lanning. The netflix prize. In Proceedings of the KDD Cup Workshop 2007, pages 3–6, New York, Aug. 2007.
[4] L. Breiman. Random forests. Maching Learning, 45(1):5–32, Oct. 2001.
[5] C. Burges. From ranknet to lambdarank to lambdamart: An overview. Learning, 11:23–581, 2010.
[6] O. Chapelle and Y. Chang. Yahoo! Learning to Rank Challenge Overview. Journal of Machine Learning Research - W & CP, 14:1–24, 2011.
[7] T. Chen, H. Li, Q. Yang, and Y. Yu. General functional matrix factorization using gradient boosting. In Proceeding of 30th International Conference on Machine Learning (ICML’13), volume 1, pages 436–444, 2013.
[8] T. Chen, S. Singh, B. Taskar, and C. Guestrin. Efficient second-order gradient boosting for conditional random fields. In Proceeding of 18th Artificial Intelligence and Statistics Conference (AISTATS’15), volume 1, 2015.
[9] R.-E. Fan, K.-W. Chang, C.-J. Hsieh, X.-R. Wang, and C.-J. Lin. LIBLINEAR: A library for large linear classification. Journal of Machine Learning Research, 9:1871–1874, 2008.
[10] J. Friedman. Greedy function approximation: a gradient boosting machine. Annals of Statistics, 29(5):1189–1232, 2001.
[11] J. Friedman. Stochastic gradient boosting. Computational Statistics & Data Analysis, 38(4):367–378, 2002.
[12] J. Friedman, T. Hastie, and R. Tibshirani. Additive logistic regression: a statistical view of boosting. Annals of Statistics, 28(2):337–407, 2000.
[13] J. H. Friedman and B. E. Popescu. Importance sampled learning ensembles, 2003.
[14] M. Greenwald and S. Khanna. Space-efficient online computation of quantile summaries. In Proceedings of the 2001 ACM SIGMOD International Conference on Management of Data, pages 58–66, 2001.
[15] X. He, J. Pan, O. Jin, T. Xu, B. Liu, T. Xu, Y. Shi, A. Atallah, R. Herbrich, S. Bowers, and J. Q. n. Candela. Practical lessons from predicting clicks on ads at facebook. In Proceedings of the Eighth International Workshop on Data Mining for Online Advertising, ADKDD’14, 2014.
[16] P. Li. Robust Logitboost and adaptive base class (ABC) Logitboost. In Proceedings of the Twenty-Sixth Conference Annual Conference on Uncertainty in Artificial Intelligence (UAI’10), pages 302–311, 2010.
[17] P. Li, Q. Wu, and C. J. Burges. Mcrank: Learning to rank using multiple classification and gradient boosting. In Advances in Neural Information Processing Systems 20, pages 897–904. 2008.
[18] X. Meng, J. Bradley, B. Yavuz, E. Sparks, S. Venkataraman, D. Liu, J. Freeman, D. Tsai, M. Amde, S. Owen, D. Xin, R. Xin, M. J. Franklin, R. Zadeh, M. Zaharia, and A. Talwalkar. MLlib: Machine learning in apache spark. Journal of Machine Learning Research, 17(34):1–7, 2016.
[19] B. Panda, J. S. Herbach, S. Basu, and R. J. Bayardo. Planet: Massively parallel learning of tree ensembles with mapreduce. Proceeding of VLDB Endowment, 2(2):1426–1437, Aug. 2009.
[20] F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot, and E. Duchesnay. Scikit-learn: Machine learning in Python. Journal of Machine Learning Research, 12:2825–2830, 2011.
[21] G. Ridgeway. Generalized Boosted Models: A guide to the gbm package.
[22] S. Tyree, K. Weinberger, K. Agrawal, and J. Paykin. Parallel boosted regression trees for web search ranking. In Proceedings of the 20th international conference on World wide web, pages 387–396. ACM, 2011.
[23] J. Ye, J.-H. Chow, J. Chen, and Z. Zheng. Stochastic gradient boosted distributed decision trees. In Proceedings of the 18th ACM Conference on Information and Knowledge Management, CIKM ’09.
[24] Q. Zhang and W. Wang. A fast algorithm for approximate quantiles in high speed data streams. In Proceedings of the 19th International Conference on Scientific and Statistical Database Management, 2007.
[25] T. Zhang and R. Johnson. Learning nonlinear functions using regularized greedy forest. IEEE Transactions on Pattern Analysis and Machine Intelligence, 36(5), 2014.