参考:https://mp.weixin.qq.com/s/A4ogzRG5AFMLer5HyNFMFg
文章目录
简述
图是一种重要的数据结构,属于一种复杂的非线性结构,由顶点的有穷非空集合和顶点之间边的集合组成,前述专题的数据结构大多为线性表和树两类结构,其中线性表中的元素是“一对一”的关系,树中的元素是“一对多”的关系,而图结构中的元素则是“多对多”的关系。下面一起来看看
图的定义
图是由顶点的有穷非空集合和顶点之间边的集合组成,通过表示为G(V,E),其中,G标示一个图,V是图G中顶点的集合,E是图G中边的集合。
(1)无向图
由顶点和边构成
(2)有向图
由顶点和有向边构成
(3)完全图
如果任意两个顶点之间都存在边叫完全图,有向的边叫有向完全图。如果无重复的边或者顶点到自身的边叫简单图
图的存储结构
图的存储结构分为邻接矩阵和邻接表两种。
(1)邻接矩阵:图的邻接矩阵存储方式是用两个数组来表示,一个一维数组存储图顶点的信息,一个二维数组(称为邻接矩阵)存储图中边或者弧的信息。
(2)邻接表:邻接表示一个有单链表组成的数组(也就是数组+链表) ,数组的大小等于图中顶点的个数,无向图的链的第一个元素是本顶点,后继分别连接着和这个顶点相连的顶点;有向图的链第一个顶点是本顶点,后继是以本顶点为起点的边的终点,如果是有权图,可以在节点元素中设置权值属性 。
邻接矩阵适用于稠密图,即图上的任意两点之间均(差不多都)存在一条边,相比邻接矩阵,邻接表要更加节省空间。
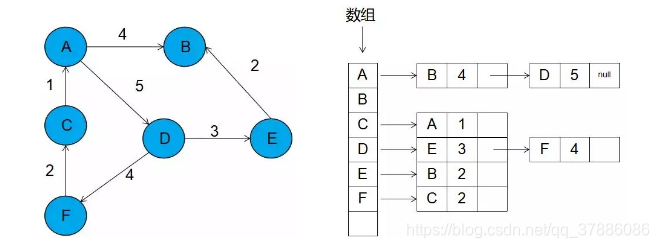
下面以邻接表存储有向带权图为例进行介绍:
注:数组存储的是所有的顶点,每一个顶点后面连接的块代表前面顶点所指向的顶点和路线的权值,如果该点还指向其他顶点,则继续在块后面添加。
图的搜索
图的搜索就是逐个访问图中的所有顶点,由于图中多对多的关系,可能存在重复访问同一顶点,所以为了避免这种情况,在图的结构设计时设置了一个布尔型数组,来确定某一顶点是否已经被遍历。
常用的遍历图的方法有两种:广度优先法和深度优先法
(1)深度优先搜索(Depth First Search)
和树的先序遍历比较类似
搜索思路:假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
显然,深度优先搜索是一个递归的过程。
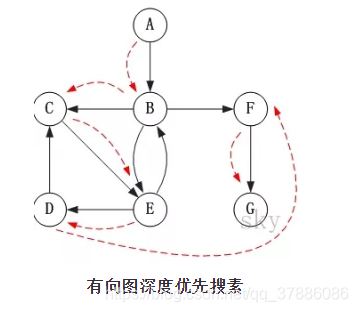
有向图深度优先搜素
注:上述图片来自
https://blog.csdn.net/hehuanchun0311/article/details/80168109
(2)广度优先搜索(Breadth First Search)
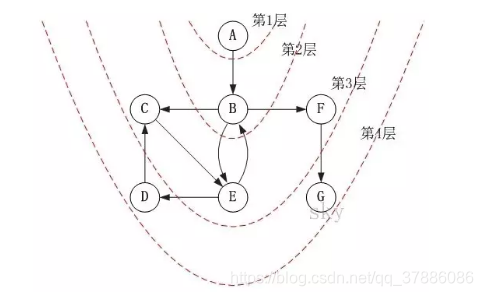
是一个分层搜索的过程,和树的层序遍历算法类同
搜索思路:从图中某顶点v出发,在访问了v之后依次访问v的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使得“ 先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问 ”,直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问,则需要另选一个未曾被访问过的顶点作为新的起始点,重复上述过程,直至图中所有顶点都被访问到为止。
注:上述图片来自
https://blog.csdn.net/hehuanchun0311/article/details/80168109
实例解析
题目1:最小高度树
题目描述:对于一个具有树特征的无向图,我们可选择任何一个节点作为根。图因此可以成为树,在所有可能的树中,具有最小高度的树被称为最小高度树。给出这样的一个图,写出一个函数找到所有的最小高度树并返回他们的根节点
格式:该图包含 n 个节点,标记为 0 到 n - 1。给定数字 n 和一个无向边 edges 列表(每一个边都是一对标签)。你可以假设没有重复的边会出现在 edges 中。由于所有的边都是无向边, [0, 1]和 [1, 0] 是相同的,因此不会同时出现在 edges 里。
示例1:
输入: n = 4, edges = [[1, 0], [1, 2], [1, 3]]
0
|
1
/ \
2 3
输出: [1]
示例2:
输入: n = 6, edges = [[0, 3], [1, 3], [2, 3], [4, 3], [5, 4]]
0 1 2
\ | /
3
|
4
|
5
输出:[3, 4]
解题思路:(1)构建图;(2)环遍历图,找出叶子节点;(3)去除叶子节点;(4)直到图中节点只剩下2个或1个,返回剩下的节点。
注:下面代码可左右滑动查看
class Solution {
private boolean[][] graph;
private boolean[] visited;
private int[] e;
private Queue<Integer> queue;
public List<Integer> findMinHeightTrees(int n, int[][] edges) {
graph = new boolean[n][n];
visited = new boolean[n];
e = new int[n];
queue = new LinkedList<>();
//初始化建图
for(int i = 0; i < edges.length; i++){
graph[edges[i][0]][edges[i][1]] = true;
graph[edges[i][1]][edges[i][0]] = true;
e[edges[i][0]]++;
e[edges[i][1]]++;
}
//去除最外层的节点
while(n>2){
//遍历图,找到最外层节点
findOuter();
while(!queue.isEmpty()){
Integer v = queue.poll();
e[v]--;
n--;
visited[v] = true;
for(int i = 0; i < graph[v].length; i++){
if(graph[v][i]){
e[i]--;
graph[v][i] = false;
graph[i][v] = false;
}
}
}
}
List<Integer> rt = new ArrayList<>();
for(int i = 0; i < visited.length; i++){
if(!visited[i]){
rt.add(i);
}
}
return rt;
}
public void findOuter(){
for(int i = 0; i<e.length; i++){
if(e[i] == 1){
queue.add(i);
}
}
}
}
题目2:重新安排行程
题目描述:给定一个机票的字符串二维数组 [from, to],子数组中的两个成员分别表示飞机出发和降落的机场地点,对该行程进行重新规划排序。所有这些机票都属于一个从JFK(肯尼迪国际机场)出发的先生,所以该行程必须从 JFK 出发。
说明:
(1)如果存在多种有效的行程,你可以按字符自然排序返回最小的行程组合。例如,行程 [“JFK”, “LGA”] 与 [“JFK”, “LGB”] 相比就更小,排序更靠前
(2)所有的机场都用三个大写字母表示(机场代码)。
(3)假定所有机票至少存在一种合理的行程。
示例 1:
输入: [[“MUC”, “LHR”], [“JFK”, “MUC”], [“SFO”, “SJC”], [“LHR”, “SFO”]]
输出: [“JFK”, “MUC”, “LHR”, “SFO”, “SJC”]
示例 2:
输入: [[“JFK”,“SFO”],[“JFK”,“ATL”],[“SFO”,“ATL”],[“ATL”,“JFK”],[“ATL”,“SFO”]]
输出: [“JFK”,“ATL”,“JFK”,“SFO”,“ATL”,“SFO”]
解释: 另一种有效的行程是
[“JFK”,“SFO”,“ATL”,“JFK”,“ATL”,“SFO”]。但是它自然排序更大更靠后。
解题思路:(1)构建图;(2)对列表排序;(3)深度优先搜素;(4)回溯。
注:下面代码可左右滑动查看
class Solution {
public boolean tag = false;//判断是否找到路线
public List<String> findItinerary(String[][] t) {
Map<String,ArrayList<String>> map = new TreeMap<>();
//构图
for(String[] str:t){
if(!map.containsKey(str[0])) map.put(str[0],new ArrayList<>());
map.get(str[0]).add(str[1]);
}
//对列表排序
for(String s:map.keySet()){
Collections.sort(map.get(s));
}
List<String> res = new ArrayList<>();
dfs(res,map,"JFK",t.length,new HashSet<>(),"");
return res;
}
public void dfs(List<String> res,Map<String,ArrayList<String>> map,String curString,int len,Set<String> set,String s){
res.add(curString);
//下面的条件为找到合适路线
if(res.size() == len + 1) {
tag = true;
return ;
}
//下面的情况为去了一个没有票离开的站点
if(map.get(curString) == null) {
set.remove(s);//回溯,即这张票归为未用状态
res.remove(res.size() - 1);//从路线中删除该站
return;
}
//深度优先遍历
//使用Set存储当前站 到 某一个站的票已用。
for(int i = 0; i < map.get(curString).size(); i++){
String str = map.get(curString).get(i);
if(!set.contains(curString + "*" + i)){
set.add(curString + "*" + i);
dfs(res,map,str,len,set,curString + "*" + i);
if(tag){
return;
}
}
}
//回溯
set.remove(s);
res.remove(res.size() - 1);
}
}