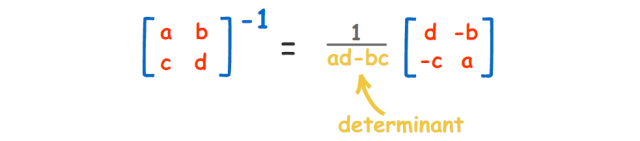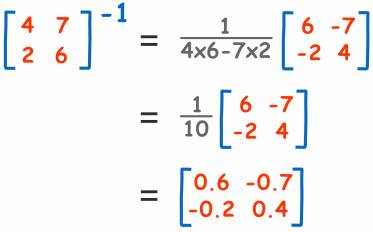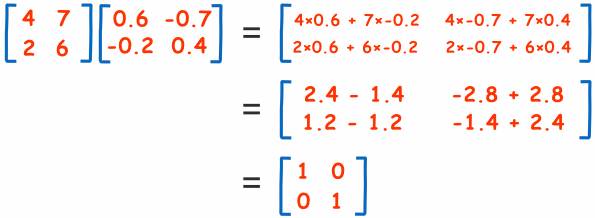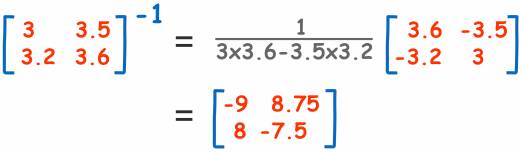本文转载自http://www.sohu.com/a/226465524_224832，讲得非常好

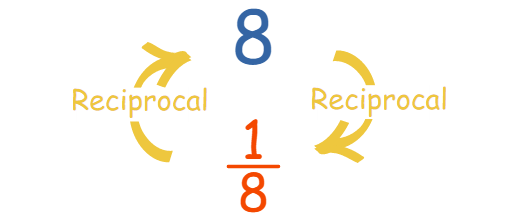
首先，我们先来看看这个数的倒数：

·倒数

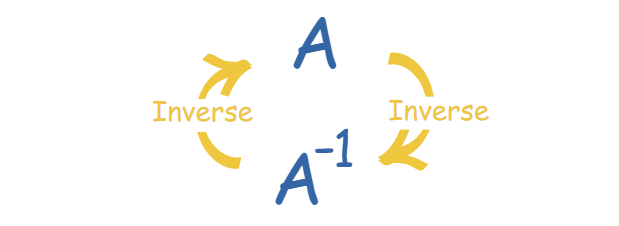
其实矩阵的逆矩阵也跟倒数的性质一样，不过只是我们习惯用A-1表示：

问题来了，既然是和倒数的性质类似，那为什么不能写成1/A？

其实原因很简单，主要是因为矩阵不能被除。不过 1/8倒可以被写成 8-1。

那矩阵的逆和倒数还有其他相似之处吗？

• 当我们将一个数乘以它的倒数我们得到1。

8 × (1/8) = 1

• 当一个矩阵乘以逆时，我们得到了单位矩阵（而单位矩阵，其实也就是矩阵中的“1”）。

A × A-1 = I

• 而此时我们将矩阵的逆放在前面，很明显，结果还是一样的

(1/8) × 8 = 1

A-1 × A = I

模友：超模君，刚才讲的“单位矩阵”是什么意思，你还没说明呢

超模君：别急，慢慢来！关于单位矩阵，其实就是一个相当于数字“1”的矩阵：

·3x3的单位矩阵

那怎样的矩阵才是单位矩阵呢？

①它是“正方形”（行数与列数相同）；

②它的对角线上的数字都是1，其他地方都是0。

• 那问题来了，我们该如何去计算矩阵的逆呢？

换句话说：交换a和d的位置，将负数置于b和c的前面，并将所有事物除以行列式（ad-bc）

举个栗子：

不过该如何去判断这是正确的答案呢？

那这个时候就要用到我们最开始讲的公式：

A × A-1 = I

所以，让我们检查一下，当我们将矩阵乘以矩阵的逆时，会是怎样的？

嘿嘿嘿嘿！我们最终得到了单位矩阵！

留个作业：试试这样，能不能得到单位矩阵呢？

其实，在了解矩阵的过程中，总是会有个疑问：为什么我们需要矩阵的逆呢？

其主要原因是：矩阵没办法被除。（这个时间各位模友可以回想一下：是不是从来都没看过矩阵被除）

换句话说，矩阵根本就没有被除的概念。

而矩阵的逆，正好是被我们用来解决“矩阵除法”的问题。

各位模友，假如我们没有“除法”这个规则，那当有人问你“如何把10分苹果平分给两个人”。

想到怎么解答没？

那我们是不是可以采取2的倒数（1/2=0.5）来计算，那答案就很清晰啦：

10 × 0.5 = 5

也就是每个人5个苹果。

那我们是不是也可以将同样的方法应用到矩阵上呢？

那故事就这么开始了，我们知道矩阵A和矩阵B，并且想要找到矩阵X。

XA = B

那最好的方法就是直接除以A（得到X = B / A），但事实上我们不能直接除以矩阵A。

但是我们却可以在公式两边都乘以A-1:

XAA-1= BA-1

因为我们都知道AA-1=I，所以也就能得到

XI = BA-1

而此时单位矩阵I我们是可以直接去掉的，也就能得到：

X = BA-1

所以呢，此时我们只要知道怎么计算A-1，那就可以直接算出矩阵X（而对于计算A-1早已解决）。

丢个栗子：

有一个几个家庭组团出去旅行，出发的时候是乘坐大巴，每位儿童3元，每个大人3.2元，一共花费了118.4元。

在回程时，他们选择乘坐火车，每名儿童3.5元，每名成人3.6元，总计135.20元。

那问题来了，这里边有多少个小孩和大人呢？

虽然这道题用线性方程组来解很简单，但这次我们尝试用矩阵思维来解答。

首先，我们设置好矩阵（此时要注意好矩阵的行和列是否正确）：

那我们根据公式：

XA = B

要解决这个问题，那也就是得到矩阵A的倒数：

现在我们可以使用以下方法来解决：

X = BA-1

结果很明显，一共有16个孩子和22个大人！

• 那问题来了，矩阵的逆到底有什么用？

事实上，像这样的计算其实非常有利于工程师设计建筑物，视频游戏和计算机动画等许多地方。

此外，它也是解决线性方程组的一种方法。

虽然求矩阵的逆，只要打开MATLAB, 输入inv(A)。

但超模君这里就要插一句话：

虽然这个过程是由计算机完成，但我们还是有必要去了解公式，因为这正是数学的美妙之处！