蒙特卡洛算法

蒙特卡洛算法（Monte Carlo Algorithm）是一种利用随机抽样进行数值计算的方法，广泛应用于各种领域，如物理学、金融工程、计算数学等。它通过在问题空间中随机生成样本来近似估计数学期望、积分或概率分布。

蒙特卡洛算法的基本原理

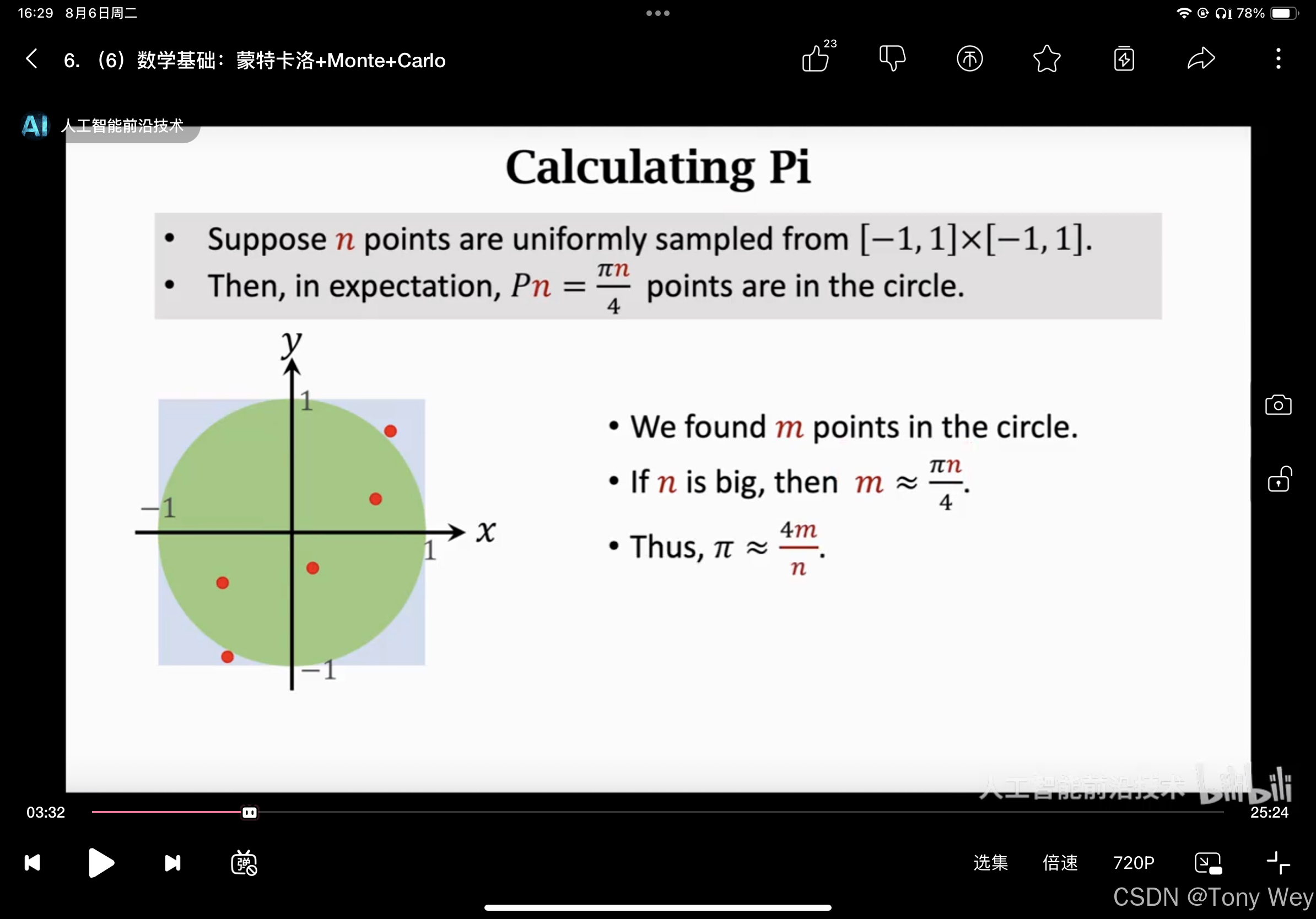
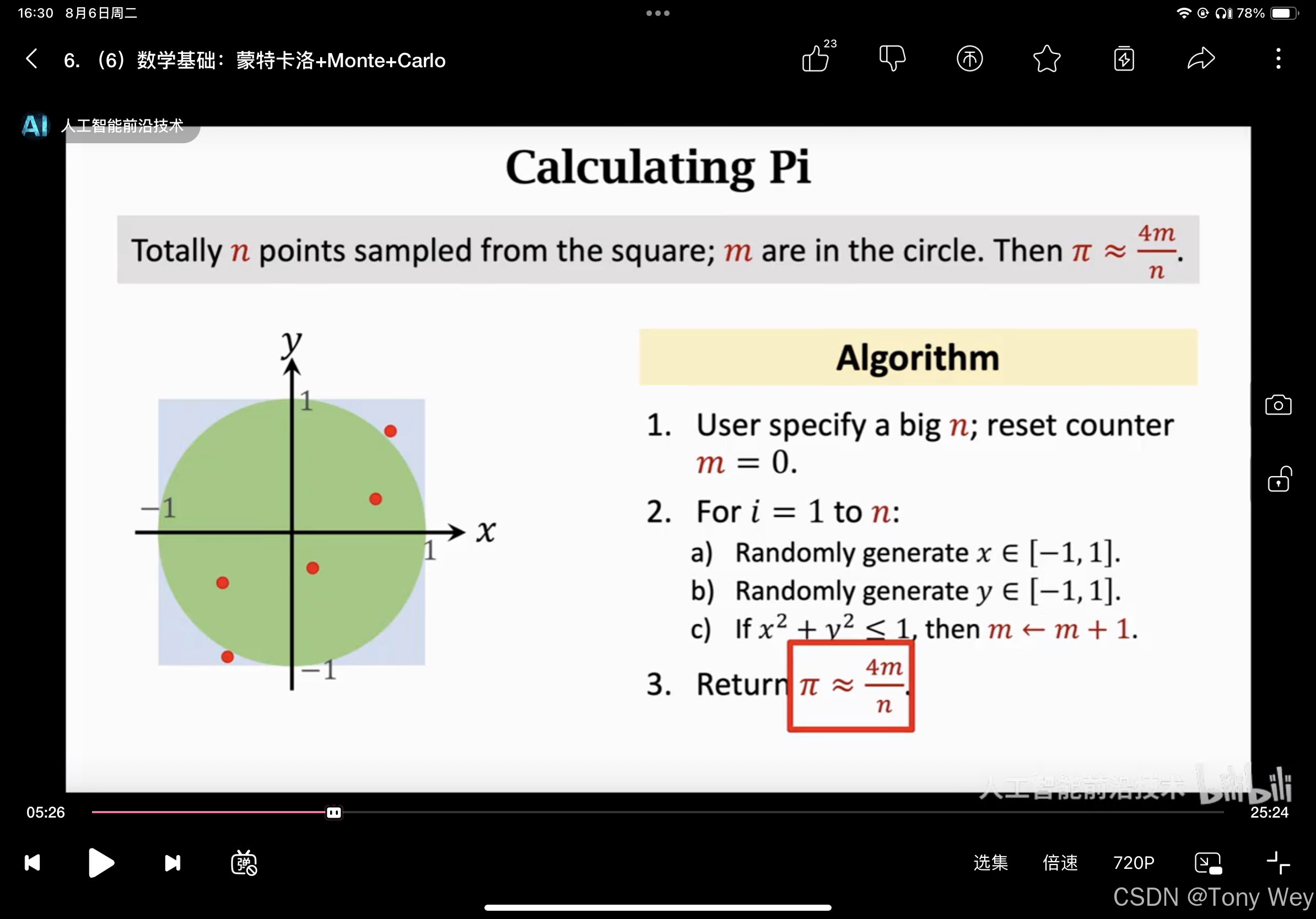
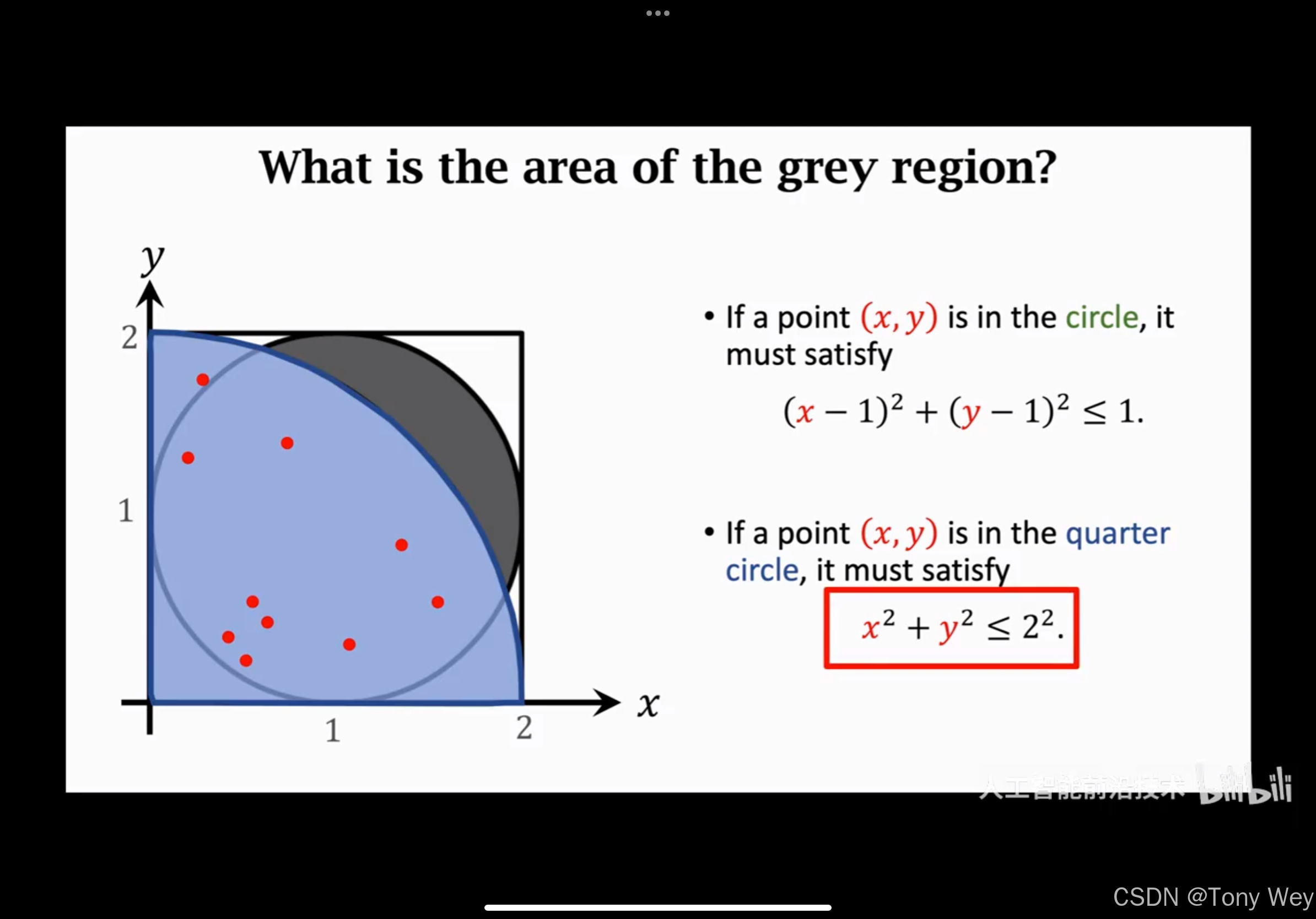
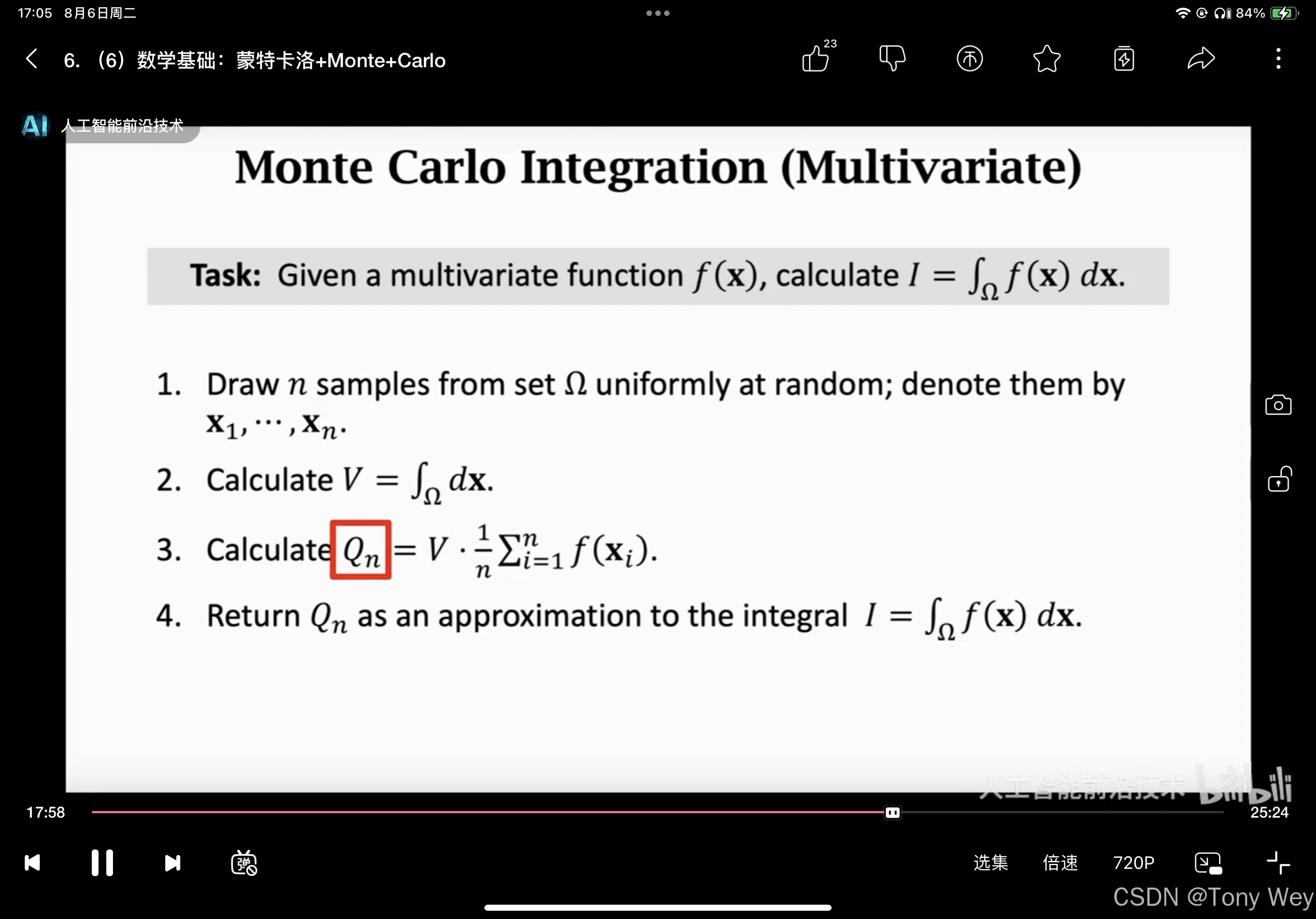
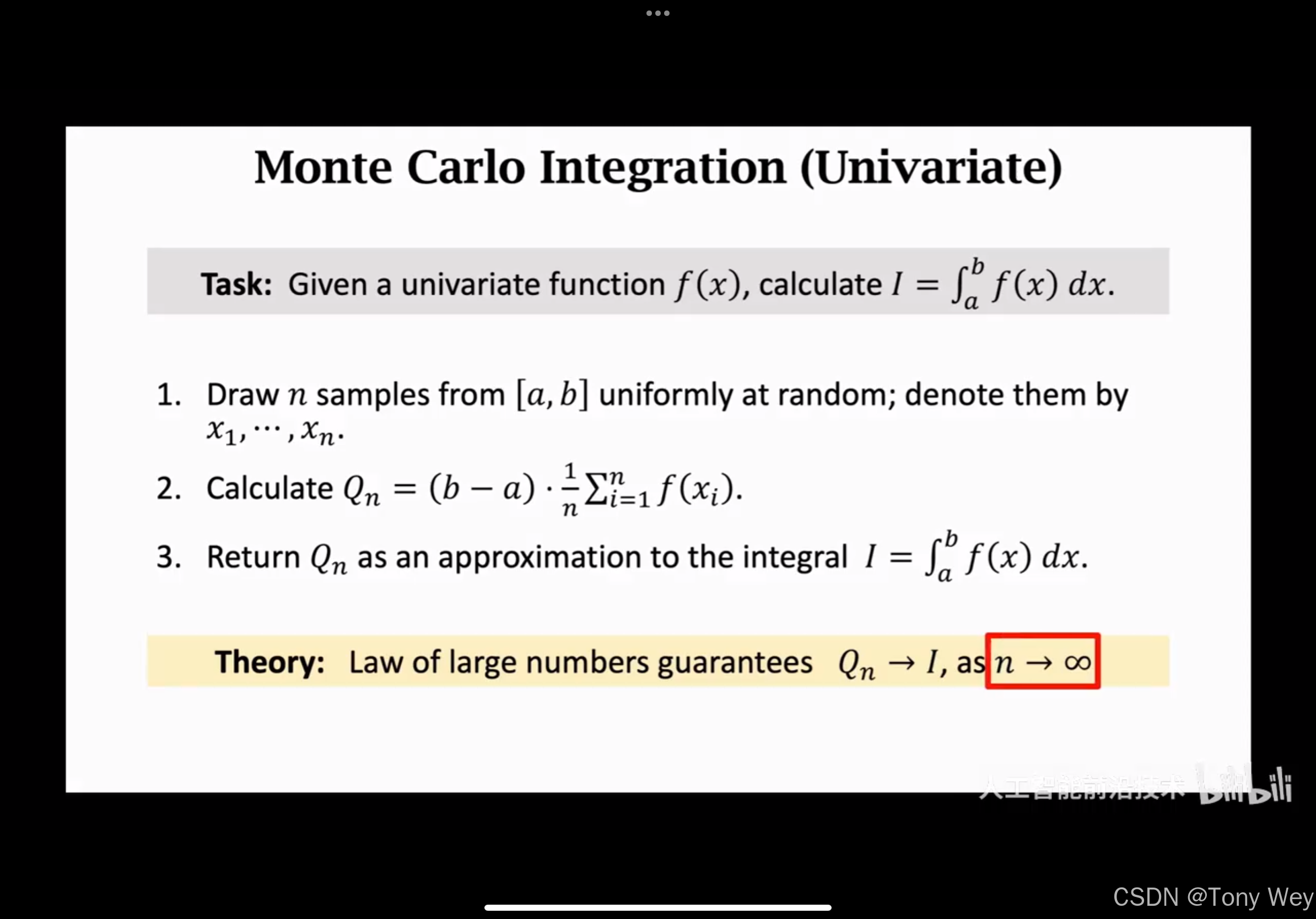
蒙特卡洛算法的基本思想是通过随机样本的平均值来逼近期望值或概率。它通常用于解决传统解析方法难以处理的问题。

蒙特卡洛算法的步骤

1. 定义问题：

   • 明确要估计的量，如积分、期望值或概率。

2. 随机抽样：

   • 在定义的概率空间中生成随机样本。样本的数量通常决定了结果的精度。

3. 计算样本函数值：

   • 对每个随机样本，计算目标函数值。

4. 估计期望值：

   • 通过样本的平均值来估计目标函数的期望值或概率。

5. 误差分析：

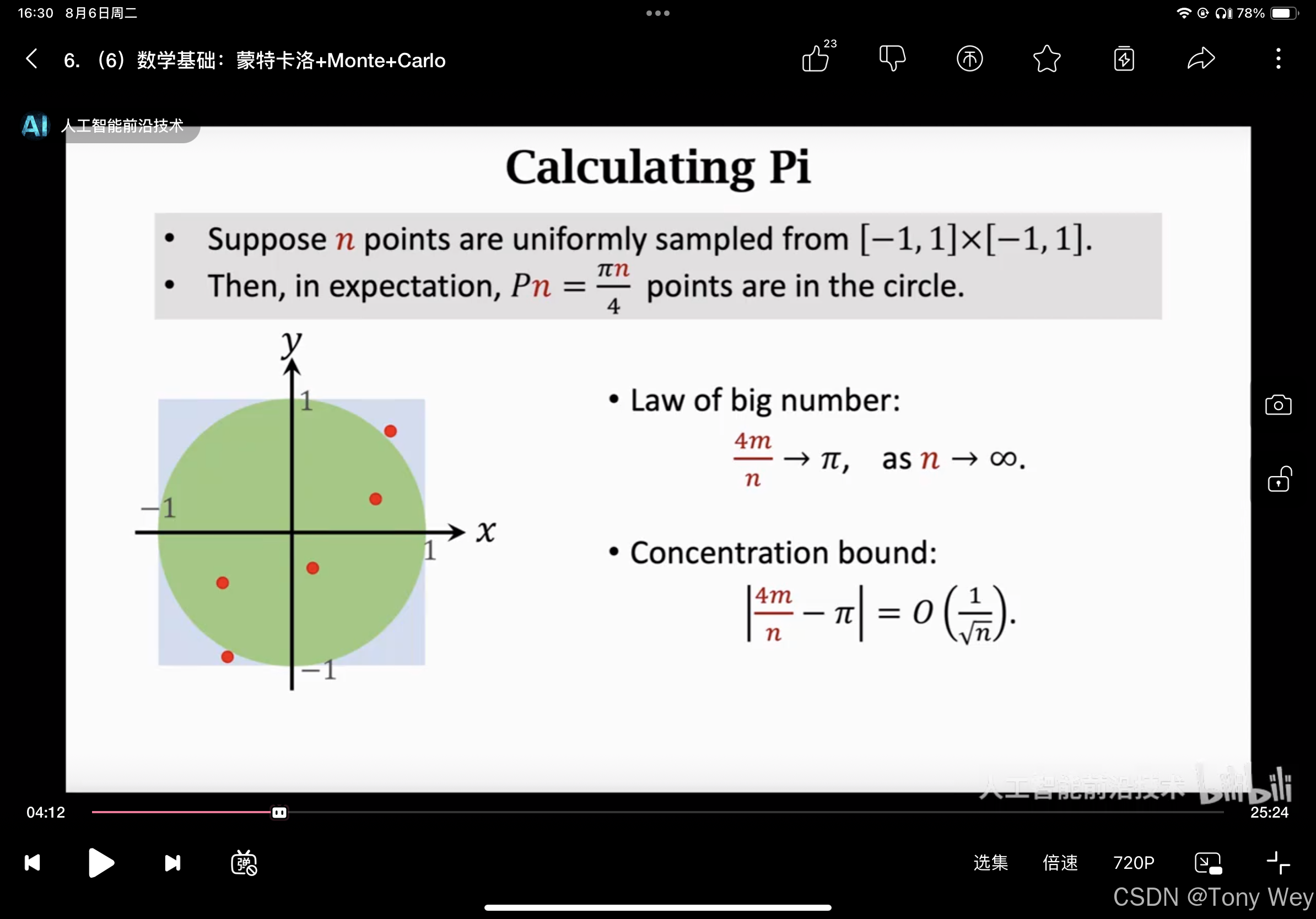
   • 通过增大样本数量来减少估计误差，通常误差与样本数量的平方根成反比。

蒙特卡洛算法的应用

1. 数值积分：

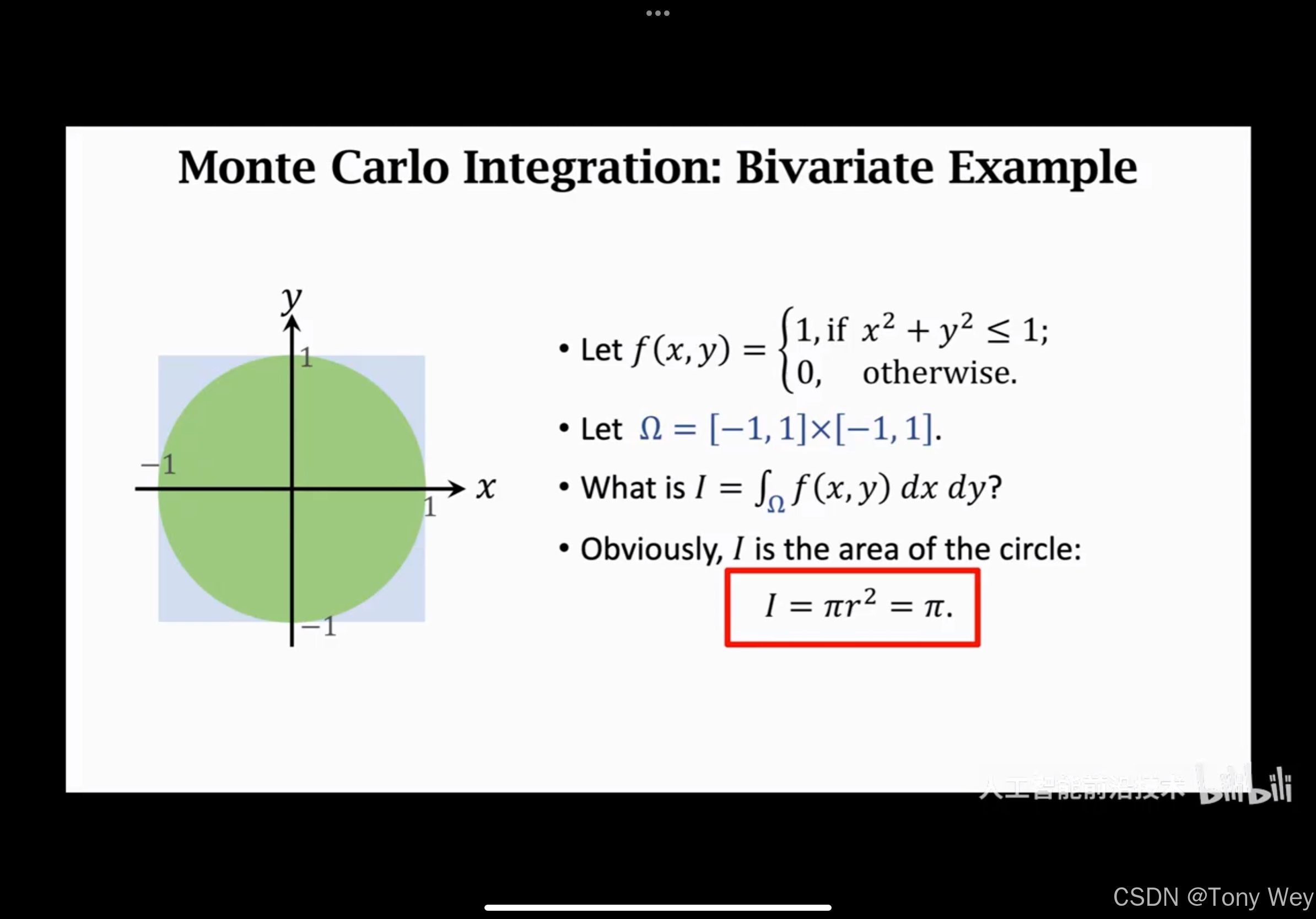
   • 在高维空间中，蒙特卡洛算法可以用于计算复杂函数的积分。

2. 金融工程：

   • 用于期权定价、风险评估等金融问题，通过模拟大量路径来近似求解。

3. 物理模拟：

   • 模拟粒子在物理系统中的运动，如气体分子运动模拟。

4. 优化问题：

   • 在求解复杂优化问题时，蒙特卡洛方法通过随机搜索空间来找到接近最优解。

蒙特卡洛算法的特点

• 灵活性：

  • 适用于多种复杂问题，尤其是在高维空间中。

• 易实现性：

  • 由于基于随机采样，蒙特卡洛算法的实现相对简单。

• 精度与样本数：

  • 算法精度依赖于样本数量，样本数越多，结果越接近真实值。

• 计算开销：

  • 在需要高精度时，计算开销较大，因为需要大量样本。

总结

蒙特卡洛算法通过随机抽样提供了一种灵活的数值计算方法，适用于解决各种复杂问题。尽管计算开销可能较大，但其简单易用性和广泛应用领域使其成为数值计算的重要工具。

无偏估计

无偏估计（Unbiased Estimation）是统计学中的一个重要概念，指的是一种估计量在长时间或大量重复抽样中，其期望值等于被估计的参数值。换句话说，无偏估计量不会系统性地偏离真实参数，是在平均意义下准确的。

无偏估计的定义

$$\begin{gathered} 设有参数\theta 的总体，其估计量为\hat{\theta }。如果\hat{\theta }的期望值等于参数\theta ，即： \\ E(\hat{\theta })=\theta \\ 那么\hat{\theta }被称为是\theta 的无偏估计。 \end{gathered}$$

举例说明

1. 样本均值：

   • $$\begin{gathered} 设X_1,X_2,\dots ,X_n是来自总体的独立同分布样本，其总体均值为\mu 。样本均值\bar{X}=\frac{1}{n}\sum _{i=1}^n{X}_i是\mu 的无偏估计，因为： \\ E(\bar{X})=\mu \end{gathered}$$

2. 样本方差：

   • $$样本方差s^2=\frac{1}{n-1}\sum _{i=1}^n(X_i-\bar{X}{)}^2是总体方差{\sigma }^2的无偏估计。$$

无偏估计的性质

1. 准确性：

   • 无偏估计量在统计上提供了一个准确的参数估计，没有系统性误差。

2. 一致性：

   • 虽然无偏估计量在期望上是准确的，但不一定是唯一最优的。不同的无偏估计量可能具有不同的方差。

3. 方差：

   • 无偏估计量的方差反映了估计量的离散程度，通常希望在无偏的基础上方差尽可能小。

无偏估计的应用

1. 统计推断：

   • 在统计推断中，无偏估计被广泛应用于参数估计，提供对总体特征的可靠估计。

2. 机器学习：

   • 在机器学习模型中，无偏估计用于保证模型参数的估计不会偏离真实值，特别是在模型训练和评估中。

总结

无偏估计是一种重要的估计方法，其关键特点是估计量的期望值等于真实参数值。无偏估计在统计推断和机器学习中广泛应用，提供了对参数的可靠估计。

笔记