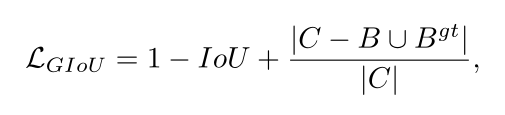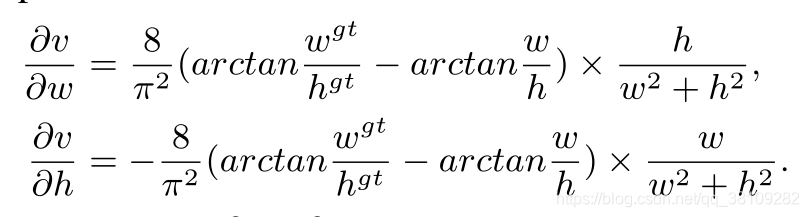前言
《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression》发表于2020年AAAI,来自天津大学和中国人名公安大学
资源
论文下载:Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression
论文题目及作者
介绍
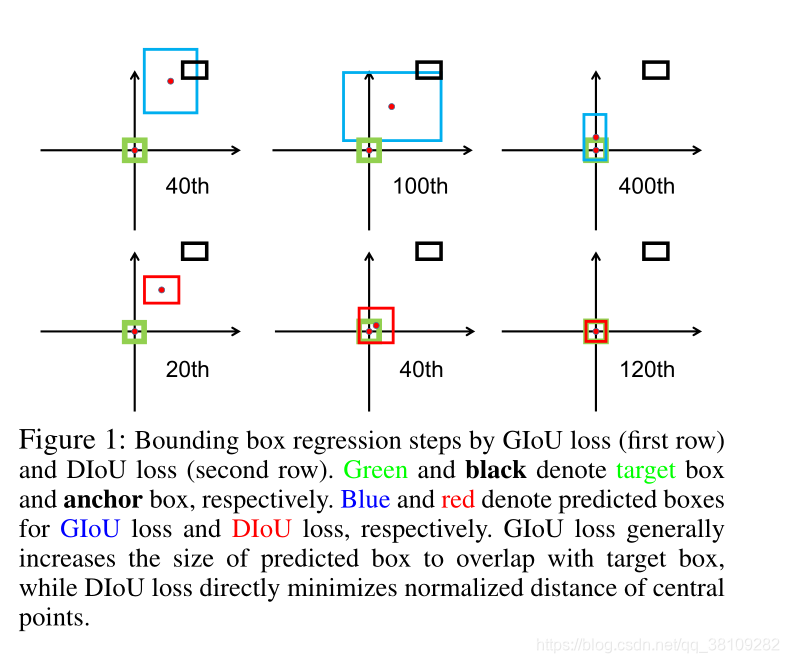
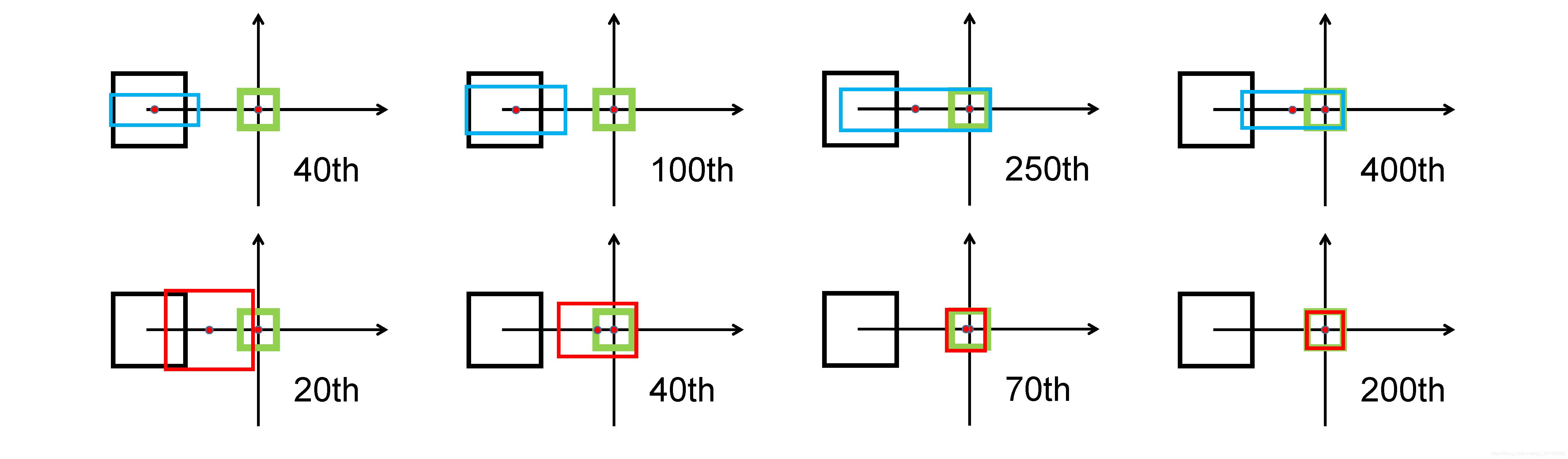
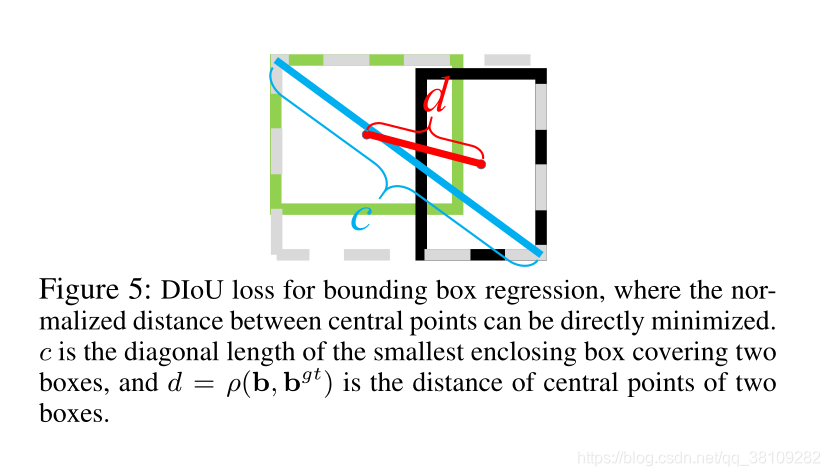
第一行为GIOU loss,第二行是DIOU loss。
绿边框表示Ground Truth,黑边框表示Anchor Box。
蓝边框和红边框表示预测框,分别用于GIOU loss和DIOU loss。
作者提到,GIOU loss通常会增加预测框的大小与Ground Truth重叠,而DIOU loss直接最小化中心点的归一化距离。
GIOU loss通常会增加预测框的大小与Ground Truth重叠:
回顾下GIOU的公式:
其中
C
C
C是
B
B
B和
B
g
t
B^{gt}
Bgt的最小闭包面积
这里作者做了迭代实验,发现GIOU loss首先通过增加预测合的大小,使其与Ground Truth重叠,然后最大化重叠区域。
DIOU loss直接最小化中心点的归一化距离:
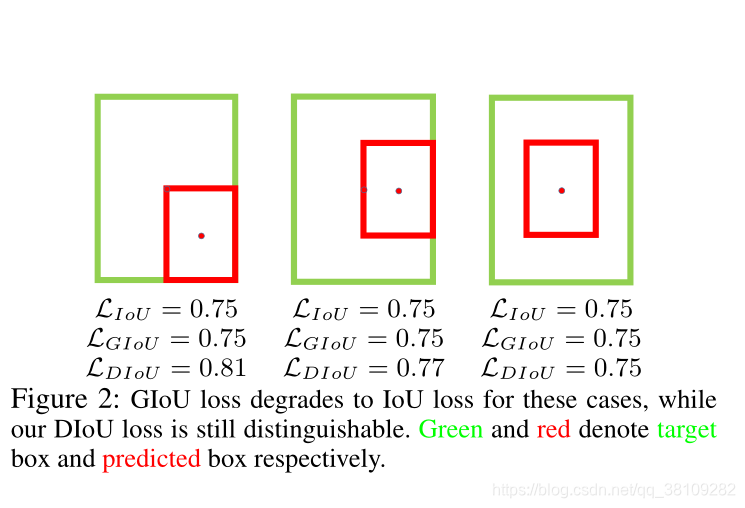
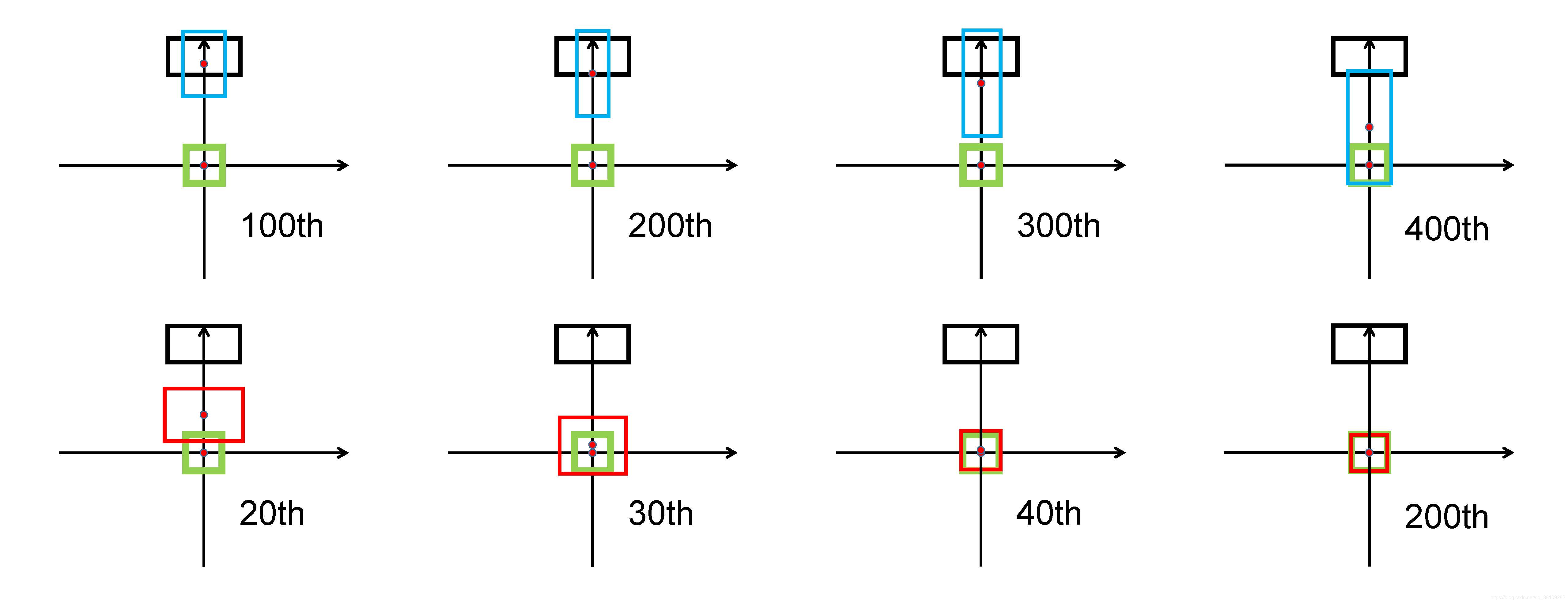
作者认为:从图2可知,GIOU loss将完全退化到IOU loss的包围框,因为GIOU loss在实验迭代中不断增加重叠区域,直至重叠区域最大。
作者画出的这个图是Ground Truth 包围了预测框,这个状态应该是由预测框主要增加宽高以增加与Ground Truth的重叠区域,然后回归坐标和宽高,详细讨论见实验部分
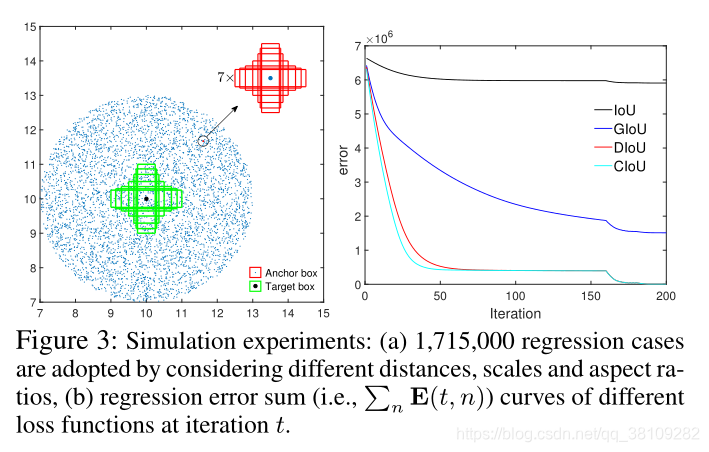
作者的仿真实验
更详细的讨论见作者的github:作者开源github
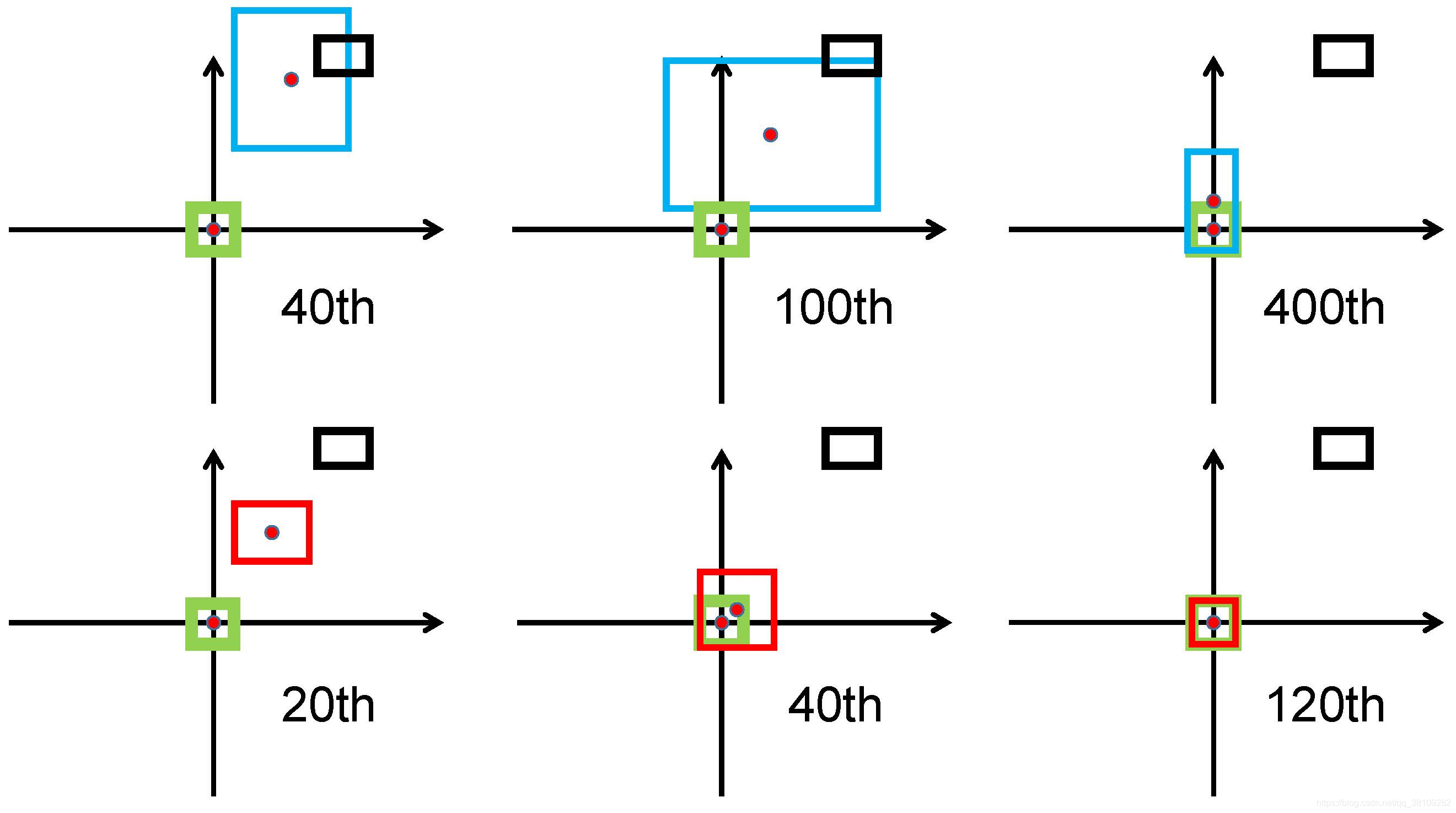
首先,将锚框设置为对角线方向。GIoU 损失通常会增加预测框的大小以与目标框重叠,而 DIoU 损失则直接最小化中心点的归一化距离。
其次,锚框设置为水平方向。GIoU 损失扩大了预测框的右边缘,而预测框的中心点仅略微向目标框移动。然后当预测框和目标框之间存在重叠时,GIoU 损失中的 IoU 项会更好地匹配。从 T = 400 处的最终结果可以看出,目标框已包含在预测框中,其中 GIoU 损失已完全降级为 IoU 损失。
第三,锚框设置为垂直方向。同样,GIoU loss 拓宽了预测框的底部边缘,这两个框在最终迭代中不匹配。相比之下,我们的 DIoU 损失仅在几十次迭代中就收敛到良好的匹配。
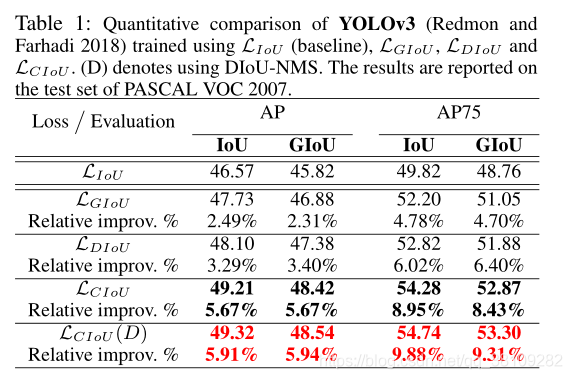
在200个epoch终止后,可见IOU以及GIOU的error在1.5,而DIOU和CIOU的error达到0,CIOU相比DIOU更快拟合。
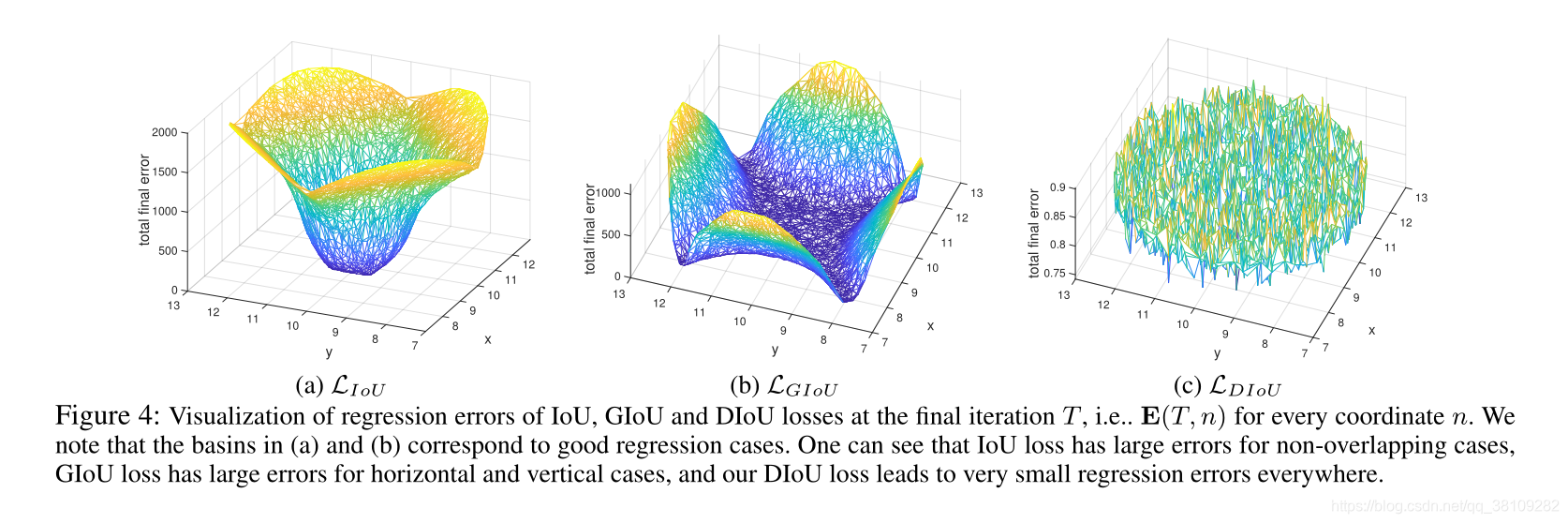
matlab仿真,盆地区域表示回归良好的情况。
作者对GIOU loss的讨论:
当Ground Truth和预测框为水平或者垂直分布时,GIOU loss大概率会产生很大的误差。这里GIOU的公式中的惩罚项是最小化
∣
C
−
B
∪
B
g
t
∣
|C-B\cup B^{gt}|
∣C−B∪Bgt∣,但是
∣
C
−
B
∪
B
g
t
∣
|C-B\cup B^{gt}|
∣C−B∪Bgt∣通常很小或者为0,即有部分重叠和包围的情况,此时GIOU loss退化到IOU loss。只要以适当的学习率运行足够多的迭代,GIOU损失将收敛到良好的解,但收敛速度非常慢。
作者的想法
作者将IOU loss 定义为:
L
=
1
−
I
o
U
+
R
(
B
,
B
g
t
)
L = 1-IoU+R(B,B^{gt})
L=1−IoU+R(B,Bgt)
其中
R
(
B
,
B
g
t
)
R(B,B^{gt})
R(B,Bgt)为预测框和Ground Truth的惩罚项,基于此提出DIOU LOSS 以及CIOU LOSS
Distance-IoU Loss
从最小化两个边界框的中心点之间的归一化距离出发,作者定义的惩罚项为:
R
D
I
o
U
=
ρ
2
(
b
,
b
g
t
)
c
2
R_{DIoU}=\frac{\rho^2(b,b^{gt})}{c^2}
RDIoU=c2ρ2(b,bgt)
其中
b
b
b和
b
g
t
b^{gt}
bgt表示
B
B
B和
B
g
t
B^{gt}
Bgt的中心点,
ρ
(
⋅
)
\rho(·)
ρ(⋅)是欧几里德距离,
c
c
c是包含
B
B
B和
B
g
t
B^{gt}
Bgt的最小闭包矩形的对角线长度。将
D
I
o
U
l
o
s
s
DIoU\ loss
DIoU loss函数定义为:
L
D
I
o
U
=
1
−
I
o
U
+
ρ
2
(
b
,
b
g
t
)
c
2
L_{DIoU}=1-IoU+\frac{\rho^2(b,b^{gt})}{c^2}
LDIoU=1−IoU+c2ρ2(b,bgt)
通过定义这样的惩罚项,该惩罚项直接最小化预测框和Ground Truth的中心点之间的距离,而GIoU loss的惩罚项旨在减小
∣
C
−
B
∪
B
g
t
∣
|C-B\cup B^{gt}|
∣C−B∪Bgt∣的面积
与IoU和GIoU loss比较
DIoU loss继承了一些IoU和GIoU loss的性质
- DIOU在回归问题的规模上仍然具有不变性
- 与GIOU loss类似,当预测框与Ground Truth重叠时,DIOU loss可以为预测框提供移动方向
- 当两个Bounding boxes完美匹配时, L I o U = L G I o U = L D I o U = 0 L_{IoU}=L_{GIoU}=L_{DIoU}=0 LIoU=LGIoU=LDIoU=0,当两个boxes相距很远时, L G I o U = L D I o U → 2 L_{GIoU}=L_{DIoU}\to 2 LGIoU=LDIoU→2
DIOU loss相比IOU和GIOU loss有几个优点
- DIOU loss可以直接最小化两个boxes的距离,因此收敛比GIOU loss更快
- 对于两个boxes有包含关系或有水平或垂直方向的情况,DIOU loss可以使回归更快,而GIOU loss几乎退化成IOU loss,即 ∣ C − B ∪ B g t ∣ → 0 |C-B\cup B^{gt}|\to 0 ∣C−B∪Bgt∣→0
Complete IoU Loss
作者认为,bounding box回归应该考虑三个重要的几何因素,即重叠区域、中心点距离和纵横比。
IOU loss考虑了重叠区域,GIOU loss大量依赖IOU loss。
提出的DIOU loss旨在同时考虑bounding box的重叠区域和中心点的距离,然而,bounding box纵横比的一致性也是重要的几何因子。
因此,基于DIOU loss,通过施加宽高比的一致性提出了CIOU loss
R
C
I
o
U
=
ρ
2
(
b
,
b
g
t
)
c
2
+
α
v
R_{CIoU}=\frac{\rho^2(b,b^{gt})}{c^2}+\alpha v
RCIoU=c2ρ2(b,bgt)+αv
其中
α
\alpha
α是一个大于零的权重系数,并且
v
v
v度量宽高比的一致性
v
=
4
π
2
(
a
r
c
t
a
n
w
g
t
h
g
t
−
a
r
c
t
a
n
w
h
)
2
v=\frac{4}{\pi^2}(arctan\frac{w^{gt}}{h^{gt}}-arctan\frac{w}{h})^2
v=π24(arctanhgtwgt−arctanhw)2
a
r
c
t
a
n
arctan
arctan函数将纵横比归一化到一个
(
−
π
2
,
π
2
)
(-\frac{\pi}{2},\frac{\pi}{2})
(−2π,2π)的区间
4
π
2
\frac{4}{\pi^2}
π24这个系数将
a
r
c
t
a
n
arctan
arctan的区间再次归一化到
(
−
1
,
1
)
(-1,1)
(−1,1)的区间
CIOU loss定义为:
L
C
I
o
U
=
1
−
I
o
U
+
ρ
2
(
b
,
b
g
t
)
c
2
+
α
v
L_{CIoU}=1-IoU+\frac{\rho^2(b,b^{gt})}{c^2}+\alpha v
LCIoU=1−IoU+c2ρ2(b,bgt)+αv
权重系数
α
\alpha
α定义为:
α
=
v
(
1
−
I
o
U
)
+
v
\alpha =\frac{v}{(1-IoU)+v}
α=(1−IoU)+vv
α
\alpha
α的分母带有重叠区域因子
1
−
I
o
U
1-IoU
1−IoU,当预测框和Ground Truth未重叠时,
1
−
I
o
U
=
1
1-IoU=1
1−IoU=1,
α
\alpha
α较小,此时
L
C
I
o
U
L_{CIoU}
LCIoU主要负责优先拟合预测框和Ground Truth的中心点坐标以及重叠区域,当预测框和Ground Truth部分重叠时,
0
<
1
−
I
o
U
<
1
0<1-IoU<1
0<1−IoU<1,
α
\alpha
α较大,
L
C
I
o
U
L_{CIoU}
LCIoU对预测框的纵横比调整加大;最后,当预测框和Ground Truth包围,
1
−
I
o
U
=
0
1-IoU=0
1−IoU=0,
α
=
1
\alpha =1
α=1达到最大值,
L
C
I
o
U
L_{CIoU}
LCIoU对预测框的纵横比调整达到最大。
假定 v v v在 1 − I o U 1-IoU 1−IoU变化时变化较小,可以忽略,则 L C I o U L_{CIoU} LCIoU在两框未重叠时对纵横比的拟合比重不大,在两框部分重叠时对纵横比的拟合加大力度,在两框包围时对纵横比的拟合达到最大力度。
由于
w
2
+
h
2
w^2+h^2
w2+h2通常是一个很小的值因为
w
w
w和
h
h
h在
[
0
,
1
]
[0,1]
[0,1]取值,这大概率会产生梯度爆炸。
因此,作者在反向传播时,移除了
1
w
2
+
h
2
\frac{1}{w^2+h^2}
w2+h21这一项,代替为1,并且作者指出梯度方向和原梯度公式一致。
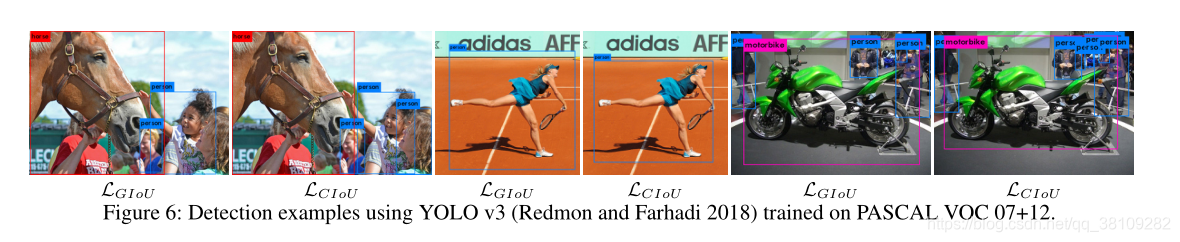
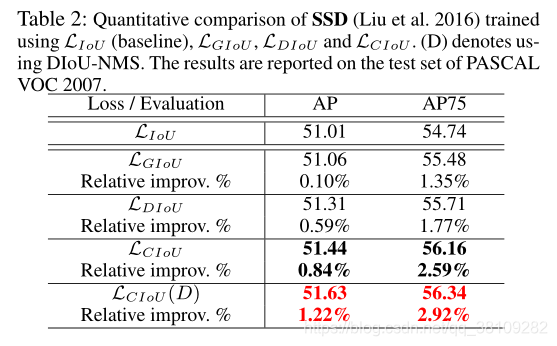
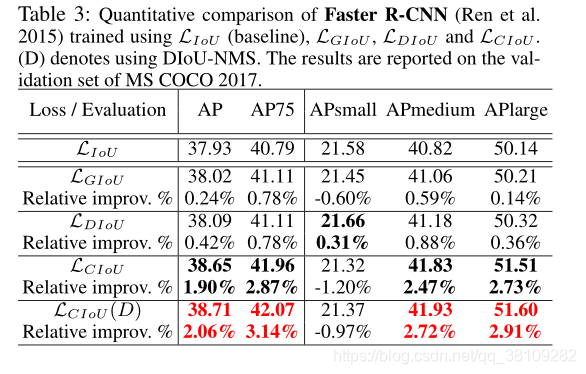
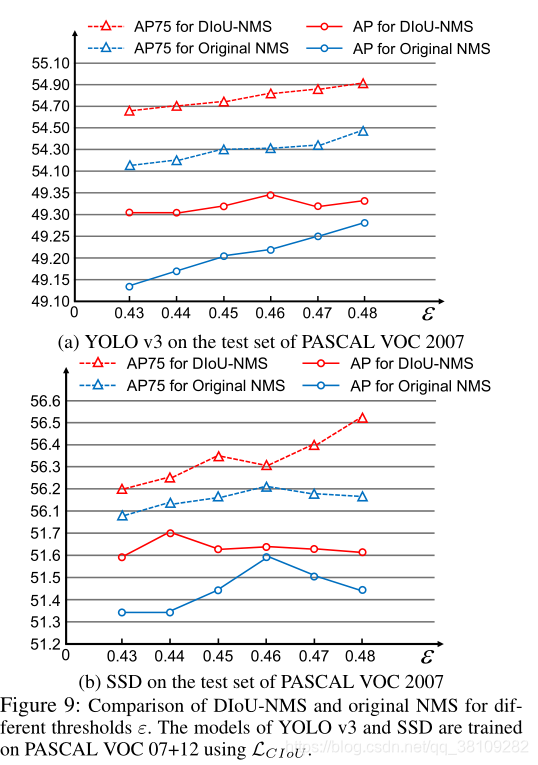
作者的实验