代码随想录算法训练营

—day34

前言

今天是算法营的第34天，希望自己能够坚持下来！
今日任务：
● 62.不同路径
● 63. 不同路径 II
● 343. 整数拆分（思路较难）
● 96. 不同的二叉搜索树（思路较难）

一、62.不同路径

题目链接
文章讲解
视频讲解

动态规划

思路：

1. dp[i][j]的定义为：走到[i,j]位置有多少种路径
2. 递归公式：对于dp[i][j]都是由上一个位置或者左边的位置移动得来，所有有
   dp[i][j] = dp[i-1][j] + dp[i][j-1]
3. 初始化：因为递推公式需要上面的位置和左边的位置来推导，所以初始化第一行和左边第一列，且走到这些位置都只有一种路径，dp[i][0] = 1, dp[0][i] = 1
4. 遍历顺序:因为递推公式是从前往后的，所以遍历顺序是从前往后

代码如下：

class Solution {
public:
    //dp[i][j]含义：走到[i,j]位置有多少种路径
    //递推公式：dp[i][j] = dp[i-1][j] + dp[i][j-1]
    //初始化: dp[i][0] = 1, dp[0][i] = 1
    //遍历顺序：左->右, 上->下
    int uniquePaths(int m, int n) {
        //int dp[m][n];
        vector<vector<int>>dp (m, vector<int>(n,0));
        for (int i = 0; i < m; i++) dp[i][0] = 1;
        for (int i = 0; i < n; i++) dp[0][i] = 1;

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }

        return dp[m-1][n-1];
    }
};

动态规划空间优化

因为实际上只跟上层对应的格子有关，左边的是由上一次递推而来，所以只需要维护一层的数组，递推公式上就是把dp[i]维度去掉。
代码如下：

class Solution {
public:
    //dp[i][j]含义：走到[i,j]位置有多少种路径
    //递推公式：dp[i][j] = dp[i-1][j] + dp[i][j-1]
    //初始化: dp[i][0] = 1, dp[0][i] = 1
    //遍历顺序：左->右, 上->下
    int uniquePaths(int m, int n) {
        vector<int>dp (n,1); //因为直接上只跟上层对应的格子有关，左边的已知了，所以只需要维护一层的数组

        for (int i = 1; i < m; i++) { //i+1：下一层
            for (int j = 1; j < n; j++) { //本层从左到右遍历
                dp[j] = dp[j] + dp[j - 1]; //本层的第j个格子=上层对应的格子+本层左边的格子
            }
        }

        return dp[n-1];
    }
};

二、63. 不同路径 II

题目链接
文章讲解
视频讲解

思路：
跟62.不同路径的区别就是多了个障碍，如果是障碍的话，就标记相应的dp[i]=0就可以了。

1. dp[i][j]的定义为：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。
2. 递归公式：因为需要考虑障碍，当(i, j)没有障碍的时候，再推导dp[i][j]
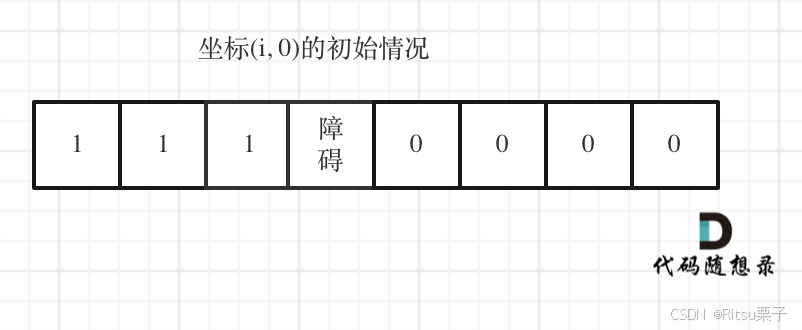
   if (obstacleGrid[i][j] == 0) dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
3. 初始化：dp[i][0]和dp[0][j]还是一样是1，但是如果有障碍的话，障碍之后（包括障碍）都是走不到的位置了，所以障碍之后的dp[i][0]应该还是初始值0。
4. 遍历顺序:因为递推公式是从前往后的，所以遍历顺序是从前往后，从上到下
   
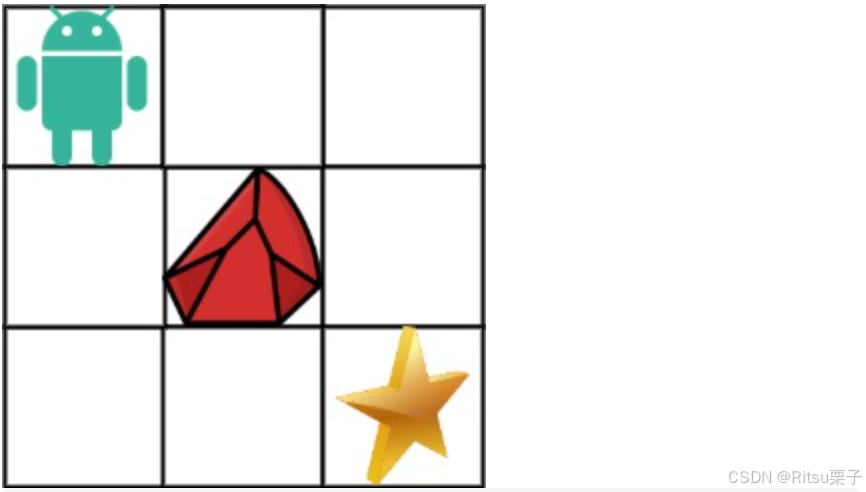
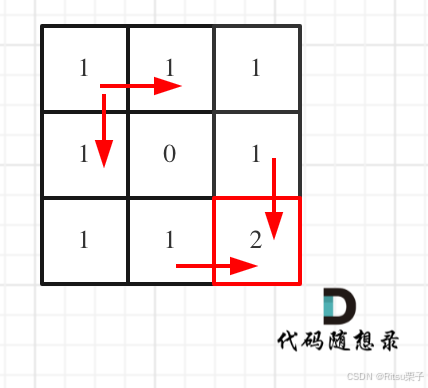
   拿示例1来举例如题：
   对应的dp table 如图：
   

动态规划

代码如下：

class Solution {
public:
    //dp[i][j]含义：走到[i,j]位置有多少种路径
    //递推公式：if(obs[i][j]!= 0) dp[i][j] = dp[i-1][j] + dp[i][j-1] 
    //初始化: dp[i][0] = 1, dp[0][i] = 1, 当遍历碰到障碍物时，后面的都是0
    //遍历顺序：左->右, 上->下
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();

        //如果在起点或终点就有障碍
        if (obstacleGrid[0][0] == 1 || obstacleGrid[m-1][n-1] == 1) return 0;

        vector<vector<int>>dp (m, vector<int>(n,0));

		//初始化，遇到障碍后终止
        for (int i = 0; i < n && obstacleGrid[0][i] == 0; i++) dp[0][i] = 1;
        for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (obstacleGrid[i][j] == 1) continue; //有障碍则跳过
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }

        return dp[m-1][n-1];
    }
};

动态规划优化空间版

同样的，因为实际上只跟上层对应的格子有关，左边的是由上一次递推而来，所以只需要维护一层的数组，递推公式上就是把dp[i]维度去掉。
代码如下：

class Solution {
public:
    //dp[i][j]含义：走到[i,j]位置有多少种路径
    //递推公式：if(obs[i][j]!= 0) dp[i][j] = dp[i-1][j] + dp[i][j-1] 
    //初始化: dp[i][0] = 1, dp[0][i] = 1, 当遍历碰到障碍物时，后面的都是0
    //遍历顺序：左->右, 上->下
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();

        //如果在起点或终点就有障碍
        if (obstacleGrid[0][0] == 1 || obstacleGrid[m-1][n-1] == 1) return 0;

        vector<int> dp(n,0);
        for (int i = 0; i < n && obstacleGrid[0][i] == 0; i++) dp[i] = 1;

        for (int i = 1; i < m; i++) {
            for (int j = 0; j < n; j++) { //这里要从0开始，因为前面只对obstacleGrid[0][i]进行了判断
                //每下一行i+1，都需要判断当前dp[0]是有障碍                                     
                if (obstacleGrid[i][j] == 1) dp[j] = 0; //这里不能用continue，不管是否有障碍，都需要更新dp[j]
                else if (j != 0)dp[j] = dp[j] + dp[j-1];
            }
        }

        return dp[n-1];
    }
};

三、343. 整数拆分

题目链接
文章讲解
视频讲解

动态规划

思路：

1. dp[i]的定义为： 对于整数i，拆分后的最大乘积
2. 递归公式：dp[i] 可能来自于两种情况：
   ①直接分出来的一个j, j与剩余的数相乘：j * (i - j)
   ②分出来j后,对剩余的数也拆分：j * dp[i-j], dp[i-j]就是对i-j进行拆分后得到最大乘积
3. 初始化：dp[0] = 0, dp[1] = 0, dp[2] = 1,那么遍历的时候就可以从3开始
4. 遍历顺序:遍历[3,n],每一个数再通过遍历[1,i]（枚举从i中拆分出来的j）求出dp[i]
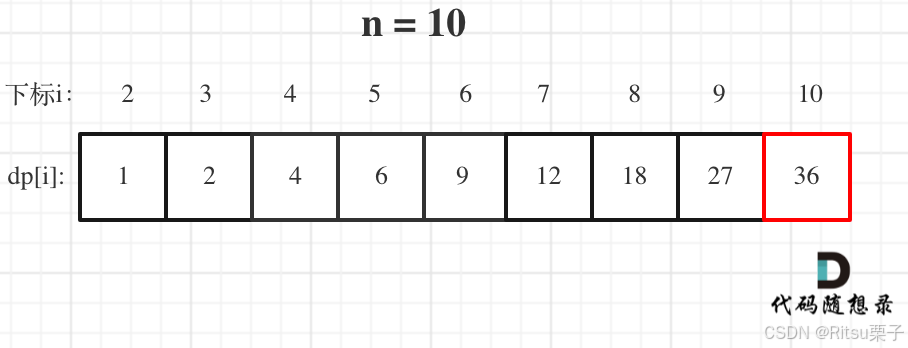
5. 举例推导dp数组：
   举例当n为10 的时候，dp数组里的数值，如下：
   

代码如下：

class Solution {
public:
    //d[i]：对于整数i，拆分后的最大乘积
    //递推公式：dp[i] 可能来自于两种情况：
    // 1、直接分出来的一个j, j与剩余的数相乘：j * (i - j) 
    // 2、分出来j后,最剩余的数也拆分：j * dp[i-j], dp[i-j]就是对i-j进行拆分后得到最大乘积
    //初始化：dp[0] = 0, dp[1] = 0, dp[2] = 1
    //遍历顺序：遍历[3,n],每一个数再通过遍历[1,i]求出dp[i]
    int integerBreak(int n) {
        vector<int> dp(n + 1, 0); //因为要求的是d[n]，创建一个n+1大小的数组
        dp[2] = 1;

        for (int i = 3; i <= n; i++) {
        	//注意 枚举j的时候，是从1开始的。从0开始的话，那么让拆分一个数拆个0，求最大乘积就没有意义了。
            for (int j = 1; j <= i/2; j++) { //这里直到i/2就结束了，因为最大乘积不会在i/2之后出现
                dp[i] = max(max((i - j) * j, j * dp[i-j]), dp[i]);
            }
        }
        return dp[n];
    }
};

贪心算法

本题也可以用贪心，每次拆成n个3，如果剩下是4，则保留4，然后相乘，但是这个结论需要数学证明其合理性！

代码如下：

class Solution {
public:
    int integerBreak(int n) {
        if (n == 2) return 1;
        if (n == 3) return 2;
        if (n == 4) return 4;
        int result = 1;
        while (n > 4) {
            result *= 3;
            n -= 3;
        }
        result *= n;
        return result;
    }
};

96.不同的二叉搜索树

题目链接
文章讲解
视频讲解

思路：

1. dp[i]的定义为：i个节点有多少种二叉搜索树
2. 递归公式：dp[i]等于遍历[1,i],计算分别以j为节点的种数累加
   以j为节点的种数又等于以j为节点后，左子树的种数*右子树的种数= dp[j-1]*dp[i-j]
3. 初始化：0个节点是1种,dp[0] = 1, 其他节点都可以通过dp[0]推出
4. 遍历顺序:因为递推公式是从前往后的，所以遍历顺序是从前往后

代码如下：

class Solution {
public:
    //dp[i]:i个节点有多少种二叉搜索树
    //递推公式：dp[i]等于遍历[1,i],计算分别以j为节点的种数累加
    //以j为节点的种数又等于以j为节点后，左子树的种数*右子树的种数= dp[j-1]*dp[i-j]
    //初始化：0个节点是1种,dp[0] = 1, 其他节点都可以通过dp[0]推出
    int numTrees(int n) {
        vector<int> dp(n + 1, 0);
        dp[0] = 1;

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[j - 1] * dp[i - j]; 
            }
        }
        return dp[n];
    }
};

总结

动态规划的dp数组，通常二维的可以优化空间去掉dp[i]维度，但是不太好理解，遍历的时候也需要一些细节上的改动。

明天继续加油！