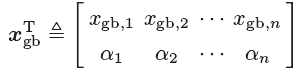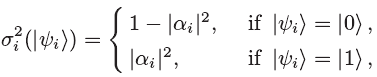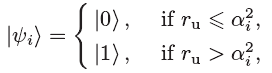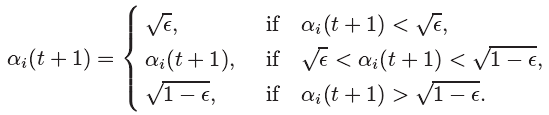智能优化算法: 基于混合量子理论的鸽群优化算法,QPIO
前言
哈喽,大家好。我是一枚小博士,今天得闲,所以马不停蹄的给大家更新我疫情期间学习的一篇优化算法文献——基于量子的鸽群优化算法(SCI文章)。
一、创新点
这篇文献的创新点有两处:一、利用一种实数编码的量子表达方式对当前迭代中的最优候选解进行重构;二、利用量子旋转门,更新量子表达。
二、鸽群算法
鸽群算法原理
鸽群算法是由北航教授段海滨等人于2014年提出的一种新的群体智能优化算法,算法主要由两部分组成:地图和指南针算子和地标算子两部分。
地图和指南针算子(Map/compass operator)
地图和指南针算子是模仿太阳和地球磁场这两种导航工具对鸽子的作用。鸽子通过磁感来感受磁场,从而在脑海中绘制地图,并把太阳当作指南针来调整方向。随着鸽群越来越逼近目的地,会逐步减少对太阳和磁性粒子的依赖。
在此阶段,鸽群算法有点类似于粒子群算法(PSO),每只鸽子同样由其位置信息和速度信息表示。在这里不做过多的原理性赘述,第
j
j
j只鸽子在第
t
t
t代的速度信息和位置信息更新策略如下:
V
j
(
t
+
1
)
=
V
j
,
s
+
r
a
n
d
∗
V
j
,
c
(
t
)
=
e
−
R
t
V
j
(
t
)
+
r
a
n
d
[
x
g
b
(
t
)
−
x
j
(
t
)
]
V_j(t+1)=V_{j,s}+rand*V_{j,c}(t)=e^{-Rt}V_j(t)+rand[x_{gb}(t)-x_j(t)]
Vj(t+1)=Vj,s+rand∗Vj,c(t)=e−RtVj(t)+rand[xgb(t)−xj(t)]
x
j
(
t
+
1
)
=
x
j
(
t
)
+
V
j
(
t
+
1
)
x_j(t+1)=x_j(t)+V_j(t+1)
xj(t+1)=xj(t)+Vj(t+1)其中,
R
R
R为罗盘算子,其取值为0.2。
地标算子(LandMark operator)
此阶段,主要针对算法的探索能力进行了提升优化。地标算子模仿导航工具地标对鸽子的影响。当鸽群接近目的地时,会依靠临近地标进行导航。如果某只鸽子熟悉地标,那么以径直飞向目的地;反之,如果不熟悉地标并且远离目的地的情况下,该只鸽子会跟随熟悉地标的其他鸽子飞行,从而到达目的地。
首先对鸽子的适应度值进行排序,然后每次迭代对其种群数量减半,假设中心鸽子熟悉地形,可以直接飞向目的地,其他的鸽子都在中心鸽子的引领下,向着目的地前进。位置更新策略如下:
N
p
(
t
)
=
N
p
(
t
−
1
)
/
2
N_p(t)=N_p(t-1)/2
Np(t)=Np(t−1)/2
X
c
=
∑
X
i
(
t
)
⋅
f
i
t
n
e
s
s
(
X
i
(
t
)
)
N
p
∑
f
i
t
n
e
s
s
(
X
c
(
t
)
−
X
i
(
t
−
1
)
)
{X_c} = \frac{{\sum {{X_i}\left( t \right) \cdot fitness\left( {{X_i}\left( t \right)} \right)} }}{{{N_p}\sum {fitness\left( {{X_c}\left( t \right) - {X_i}\left( {t - 1} \right)} \right)} }}
Xc=Np∑fitness(Xc(t)−Xi(t−1))∑Xi(t)⋅fitness(Xi(t))
X
i
(
t
)
=
X
i
(
t
−
1
)
+
r
a
n
d
⋅
(
X
c
(
t
)
−
X
i
(
t
−
1
)
)
{X_i}\left( t \right) = {X_i}\left( {t - 1} \right) + rand \cdot \left( {{X_c}\left( t \right) - {X_i}\left( {t - 1} \right)} \right)
Xi(t)=Xi(t−1)+rand⋅(Xc(t)−Xi(t−1))
基本鸽群算法流程(简)
start——
step1:初始化参数与位置信息;
step2:设置每只鸽子随机速度和位置信息,比较每只鸽子的适应度,找出当前最优解;
step3:操作地图和指南针算子。根据公式(1)(2)对鸽子的位置信息和速度信息进行更新,然后比较所有鸽子的适应度,找到新的最优解;
step4:如果迭代次数达到地图和指南针算子的迭代上限,则停止当前迭代,转而操作地标算子,否则跳转至Step3;
step5:根据鸽子的健康值对其进行排序,根据公式(3)(4)(5)操作地标算子,存储最佳位置以及最优函数值;
step6:判断迭代次数是否超过迭代上限,若超过,则输出结果,否则跳转至Step5。
Output:最优解——end
实数编码的量子表示(A real-code quantum representation)
一个量子可以通过“0”态和“1”态进行表示,即正态与伪态。量子位状态被表示为如下:
∣
ψ
⟩
=
α
∣
0
⟩
+
β
∣
1
⟩
\left| \psi \right\rangle = \alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle
∣ψ⟩=α∣0⟩+β∣1⟩,其中,
α
\alpha
α和
β
\beta
β分别代表两种状态的线性概率,且满足
α
i
2
+
β
i
2
=
1
,
(
i
=
1
,
2
,
⋯
,
n
)
\alpha _i^2 + \beta _i^2 = 1,\left( {i = 1,2, \cdots ,n} \right)
αi2+βi2=1,(i=1,2,⋯,n)在这里最优解被认为是两个状态概率的线性叠加,即“0”态和“1”态,最优解的量子表示可以更新为:
则每只鸽子的收敛方向可以重新被定义为:
d
j
,
c
=
x
^
g
−
x
j
{d_{j,c}} = {\hat x_g} - {x_j}
dj,c=x^g−xj其中,
x
^
g
{\hat x_g}
x^g是最有候选解的观测值,文献中引入一个复函数
ω
(
x
,
y
)
\omega \left( {x,y} \right)
ω(x,y),通过计算其概率密度
∣
ω
(
x
,
y
)
∣
2
{\left| {\omega \left( {x,y} \right)} \right|^2}
∣ω(x,y)∣2得到最优候选解得观测值。
∣
ω
(
x
i
)
∣
2
=
1
2
π
σ
i
exp
(
−
(
x
i
−
μ
i
)
2
2
σ
i
)
,
i
=
1
,
2
,
⋯
,
n
{\left| {\omega \left( {{x_i}} \right)} \right|^2} = {1 \over {\sqrt {2\pi } {\sigma _i}}}\exp \left( { - {{{{\left( {{x_i} - {\mu _i}} \right)}^2}} \over {2{\sigma _i}}}} \right),\quad i = 1,2, \cdots ,n
∣ω(xi)∣2=2πσi1exp(−2σi(xi−μi)2),i=1,2,⋯,n其中,
μ
i
{\mu _i}
μi和
σ
i
{\sigma _i}
σi分别代表期望值和标准差。期望值可以用当前最优候选解表示,标准差可以用下式进行计算:
最后,得到当前最优解得观测值为:
x
^
g
=
r
a
n
d
×
∣
ω
(
x
i
)
∣
2
×
(
x
i
,
max
−
x
i
,
min
)
{\hat x_{g}} = rand \times {\left| {\omega \left( {{x_i}} \right)} \right|^2} \times \left( {{x_{i,\max }} - {x_{i,\min }}} \right)
x^g=rand×∣ω(xi)∣2×(xi,max−xi,min)
综上所示,第
j
j
j只鸽子在第
t
t
t次迭代种得速度更新公式更改为:
V
j
(
t
+
1
)
=
V
j
,
s
+
r
a
n
d
∗
V
j
,
c
(
t
)
=
e
−
R
t
V
j
(
t
)
+
d
j
,
c
V_j(t+1)=V_{j,s}+rand*V_{j,c}(t)=e^{-Rt}V_j(t)+d_{j,c}
Vj(t+1)=Vj,s+rand∗Vj,c(t)=e−RtVj(t)+dj,c
量子旋转门(Quantum rotation gate, QRG)
在量子遗传算法中,由于量子编码作用下的染色体不再是单一状态,遗传操作不能继续采用传统的选择、交叉、变异操作,继而采用量子旋转门作用于量子染色体的基态,使其相互干扰、发生相位变化,从而改变
α
i
\alpha_i
αi的分布域。
这里同样使用QRG对最优解的概率幅值进行更新,通过增加旋转角度,提高
α
i
\alpha_i
αi的概率幅值,进而提高了个体朝全局最佳解的收敛速度。算法开始时,
α
i
\alpha_i
αi与
β
i
\beta_i
βi所对应的概率幅值均为
2
/
2
\sqrt2 /2
2/2。如果全局最优解在迭代结束之后发生改变,则通过量子旋转门增加
α
i
\alpha_i
αi;否则,将概率幅值全部重置为初始值,防止算法陷入局部最优。QRG具体更新策略如下:
α
i
(
t
+
1
)
=
[
cos
(
Δ
θ
)
−
sin
(
Δ
θ
)
]
[
α
i
(
t
)
1
−
[
α
i
(
t
)
]
2
]
{\alpha _i}\left( {t + 1} \right) = \left[ {\cos \left( {\Delta \theta } \right) - \sin \left( {\Delta \theta } \right)} \right]\left[ {{{{\alpha _i}\left( t \right)} \over {\sqrt {1 - {{\left[ {{\alpha _i}\left( t \right)} \right]}^2}} }}} \right]
αi(t+1)=[cos(Δθ)−sin(Δθ)]⎣⎡1−[αi(t)]2αi(t)⎦⎤
这里大家对RCQ和QRG还有疑问得地方,可以去看一下这篇文章。https://blog.xupengit.top/index.php/20181210/cid=35.html
三、文章优势分析
这篇文章得主要卖点在于用最少的个体,表达最多得种群特性。因此,QPIO算法可以用最小的种群数量解决大规模优化问题,这样就减少了算法的时间复杂度。
对比实验
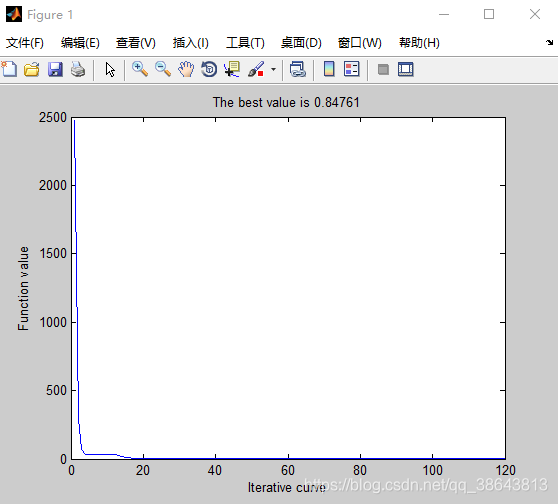
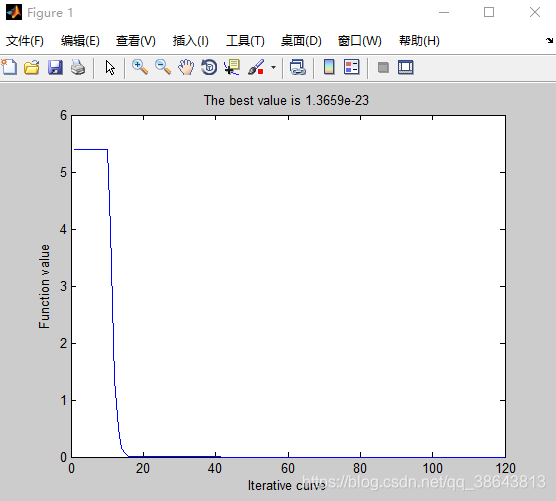
老规矩,使用CEC测试函数Sphere进行测试。其中,将种群数量population size都设置为6,观察对比结果。
分析
通过对比图片中的收敛情况,读者应该有一个直观的认识。即量子鸽群算法,可以用最少的种群来解决大规模问题,且具有更加优秀的算法性能。
这篇文章为SCI一区特刊论文,具有非常强的实用性和可拓展性,可以将此方法RCQ和QRG嫁接至其他群体智能优化算法上,继而发表一些高质量论文。
具体Matlab代码链接如下:
https://mianbaoduo.com/o/bread/aZ2ckpw=
前一段时间给大家分享的海鸥算法(SOA),就可以与这篇文章的思路进行结合,发表一篇SCI文章,我觉得应该是没问题哒,祝大家收获满满!
具体Matlab代码链接如下:
https://mianbaoduo.com/o/bread/aZqamJc=