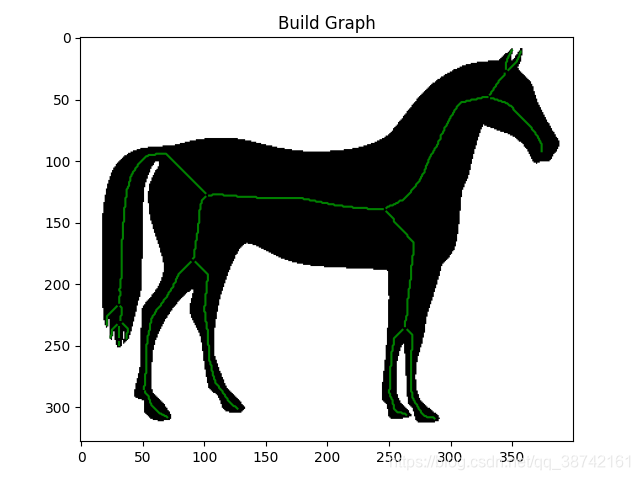
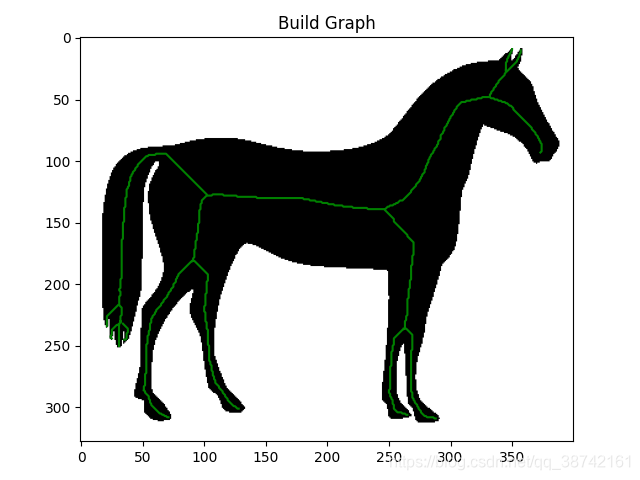
路网分割后得到region，提取骨架得到centerline，之后需要进行矢量化得到结点和边，进而转化成geojson格式进行生产。

本文对矢量化函数库sknw源码进行研读，并改进源码使结点和边之间紧密连接。

一、骨架提取并矢量化demo

from skimage.morphology import skeletonize
from skimage import data
import sknw
import numpy as np
import matplotlib.pyplot as plt

# 骨架提取
img = data.horse()
ske = skeletonize(~img).astype(np.uint16)

# 矢量化调用函数
graph = sknw.build_sknw(ske)


# draw image
plt.imshow(img, cmap='gray')

# draw edges by pts
for (s, e) in graph.edges():
    ps = graph[s][e]['pts']
    plt.plot(ps[:, 1], ps[:, 0], 'green')

# draw node by o
# node, nodes = graph._node, graph.nodes()
# ps = np.array([node[i]['o'] for i in nodes])
# plt.plot(ps[:, 1], ps[:, 0], 'r.')


# title and show
plt.title('Build Graph')
plt.show()
# plt.savefig('pc.png')

二、sknw源码研读：

①做一个像素的buffer，以免原图边界处找不到3*3邻域。

②将二值化图像进行结点映射，背景0，边1，结点2

③结点域提取，相邻结点组成一个结点域，对每个结点域进行索引编码，从10开始，依次递增。为了避免与映射012混淆，10代表第0个结点。

④遍历结点作为入口，遍历邻域寻找线，如果邻域内两次找到结点，则已遍历到的线作为这两个结点的连线。

⑤结点域找中心点

import numpy as np
from numba import jit
import networkx as nx
import matplotlib.pyplot as plt

# get neighbors d index
def neighbors(shape):
    """
    找出3*3大小的邻域，并压缩至向量的形式表示
    """
    dim = len(shape)
    block = np.ones([3]*dim)
    block[tuple([1]*dim)] = 0
    idx = np.where(block>0)
    idx = np.array(idx, dtype=np.uint8).T
    idx = np.array(idx-[1]*dim)
    acc = np.cumprod((1,)+shape[::-1][:-1])
    return np.dot(idx, acc[::-1])

@jit # my markimport m
def mark(img): # mark the array use (0, 1, 2)
    """
    将二值化的骨架图按照背景、线、结点的形式映射到0，1，2
    """
    nbs = neighbors(img.shape)
    H,W = img.shape
    img = img.ravel()
    for p in range(len(img)):
        if img[p]==0:continue
        s = 0
        for dp in nbs:
            if img[p+dp]!=0:s+=1
        if s==2:img[p]=1
        else:img[p]=2
    # image = np.zeros((H,W))
    # for i in range(len(img)):
    #     image[i//W,i-i//W*W] = img[i]
    # tmp = image[200:251,:51]
    # plt.imshow(tmp,cmap="gray")
    # plt.show()



@jit # trans index to r, c...
def idx2rc(idx, acc):
    """
    将一维向量形式的坐标映射到二维图像坐标
    """
    rst = np.zeros((len(idx), len(acc)), dtype=np.int16)
    for i in range(len(idx)):
        for j in range(len(acc)):
            rst[i,j] = idx[i]//acc[j]
            idx[i] -= rst[i,j]*acc[j]
    rst -= 1
    return rst
    
@jit # fill a node (may be two or more points)
def fill(img, p, num, nbs, acc, buf):
    """
    cur 当前遍历的结点，s 当前存储结点，该循环用以遍历所有相邻（8邻域）的node结点。
    return 二维list:以p点为中心进行拓展，找出包含p的所有密闭链接的结点。形式：[[node1_x,node2_y]...]
    """
    #back = 2
    back = img[p]
    img[p] = num
    #buf存储idx
    buf[0] = p
    cur = 0; s = 1;
    
    while True:
        p = buf[cur]
        for dp in nbs:
            cp = p+dp
            if img[cp]==back:
                img[cp] = num
                buf[s] = cp
                s+=1
        cur += 1
        if cur==s:break
    return idx2rc(buf[:s], acc)

@jit # trace the edge and use a buffer, then buf.copy, if use [] numba not works
def trace(img, p, nbs, acc, buf):
    """
    c1 头结点索引， c2 尾结点索引， 注意有着先后（小大）顺序，顺序不能乱，否则后续连线出现飞线
    newp 存储线上要遍历的下一个点。
    修改方法：我们将头尾结点添加至线的范围内，这样可以连接结点域内部结点间的线。从而生成封闭的拓扑。
    """
    c1 = 0; c2 = 0;
    newp = 0
    cur = 0
    while True:
        buf[cur] = p
        img[p] = 0
        cur += 1
        for dp in nbs:
            cp = p + dp
            if img[cp] >= 10:
                if c1==0:
                    c1=img[cp]
                    #add
                    # c1_p = cp
                else:
                    c2 = img[cp]
                    #add
                    # c2_p = cp
            if img[cp] == 1:
                newp = cp
        p = newp
        if c2!=0:break
    # #add
    # buf = np.insert(buf,0,c1_p)
    # #add
    # buf[cur+1] = c2_p
    # #add
    # cur += 2
    return (c1-10, c2-10, idx2rc(buf[:cur], acc))
   
@jit # parse the image then get the nodes and edges
def parse_struc(img):
    #img.shape H*W
    nbs = neighbors(img.shape)
    #acc: (W,1)
    acc = np.cumprod((1,)+img.shape[::-1][:-1])[::-1]
    img = img.ravel()
    #pts: 结点索引，平铺后
    pts = np.array(np.where(img==2))[0]
    buf = np.zeros(131072, dtype=np.int64)
    #num 结点索引，以10开始，为了避免mark（0 1 2）的干扰，所以从10开始代表第0个结点域（注意是一片连续的区域）。每存储一个结点域num+1。
    num = 10
    nodes = []
    for p in pts:
        if img[p] == 2:
            nds = fill(img, p, num, nbs, acc, buf)
            num += 1
            nodes.append(nds)

    edges = []
    for p in pts:
        for dp in nbs:
            if img[p+dp]==1:
                edge = trace(img, p+dp, nbs, acc, buf)
                edges.append(edge)

    return nodes, edges
    
# use nodes and edges build a networkx graph
def build_graph(nodes, edges, multi=False):
    graph = nx.MultiGraph() if multi else nx.Graph()
    for i in range(len(nodes)):
        graph.add_node(i, pts=nodes[i], o=nodes[i].mean(axis=0))
    for s,e,pts in edges:
        l = np.linalg.norm(pts[1:]-pts[:-1], axis=1).sum()
        graph.add_edge(s,e, pts=pts, weight=l)
    return graph

def buffer(ske):
    #扩充一个单位像素的边，以便对原图中每个像素进行八邻域查找
    buf = np.zeros(tuple(np.array(ske.shape)+2), dtype=np.uint16)
    buf[tuple([slice(1,-1)]*buf.ndim)] = ske
    return buf

def build_sknw(ske, multi=False):
    buf = buffer(ske)
    mark(buf)
    nodes, edges = parse_struc(buf)
    return build_graph(nodes, edges, multi)
    
# draw the graph
def draw_graph(img, graph, cn=255, ce=128):
    acc = np.cumprod((1,)+img.shape[::-1][:-1])[::-1]
    img = img.ravel()
    for idx in graph.nodes():
        pts = graph.node[idx]['pts']
        img[np.dot(pts, acc)] = cn
    for (s, e) in graph.edges():
        eds = graph[s][e]
        for i in eds:
            pts = eds[i]['pts']
            img[np.dot(pts, acc)] = ce

if __name__ == '__main__':
    g = nx.MultiGraph()
    g.add_nodes_from([1,2,3,4,5])
    g.add_edges_from([(1,2),(1,3),(2,3),(4,5),(5,4)])
    print(g.nodes())
    print(g.edges())
    a = g.subgraph(1)
    print('d')
    print(a)
    print('d')
    

最后输出每个结点域的中心点和线。但是存在结点与线分离的情况。如下图所示：

三、添加代码：结点与边相连

分析不相连的原因：结点域以结点中心区域表示，故其它结点不会显示，于是存在断线。我的思路是从线的端点开始，向外遍历并入非结点中心的结点作为线的扩充点即可。注意线的顺序，因为线的存储是有序的，头结点和尾结点的顺序正好相反。添加代码如下：

#add
def join_nodes(graph):
    node, nodes = graph._node, graph.nodes()
    center_node = np.array([node[i]['o'] for i in nodes])
    all_nodes = np.array([node[i]['pts'] for i in nodes])
    for (s, e) in graph.edges():
        ps = graph[s][e]['pts']
        s_center_node = center_node[s]
        e_center_node = center_node[e]
        s_all_nodes = all_nodes[s]
        e_all_nodes = all_nodes[e]
        s_line_point = ps[0]
        e_line_point = ps[-1]
        #线长度为一的不进行扩展，以免后续清洗不掉
        if len(ps)==1:
            continue
        if len(s_all_nodes)==1:
            graph[s][e]['pts'] = np.vstack((s_center_node,graph[s][e]['pts']))
        else:
            bbox = [min(s_center_node[0],s_line_point[0]),max(s_center_node[0],s_line_point[0]),
                    min(s_center_node[1],s_line_point[1]),max(s_center_node[1],s_line_point[1])]
            s_crop_nodes = [i for i in s_all_nodes if i[0]>=bbox[0] and i[0]<=bbox[1] and i[1]>=bbox[2] and i[1]<=bbox[3]][::-1]
            for i in s_crop_nodes:
                graph[s][e]['pts'] = np.vstack((np.array(i),graph[s][e]['pts']))

        if len(e_all_nodes)==1:
            graph[s][e]['pts'] = np.vstack((graph[s][e]['pts'],e_center_node))
        else:
            bbox = [min(e_center_node[0],e_line_point[0]),max(e_center_node[0],e_line_point[0]),
                    min(e_center_node[1],e_line_point[1]),max(e_center_node[1],e_line_point[1]),]
            e_crop_nodes = [i for i in e_all_nodes if i[0]>=bbox[0] and i[0]<=bbox[1] and i[1]>=bbox[2] and i[1]<=bbox[3]][::-1]
            for i in e_crop_nodes:
                graph[s][e]['pts'] = np.vstack((graph[s][e]['pts'],np.array(i)))
    return graph
graph = join_nodes(graph)

后处理改进结果：