机器人开发--MPC 模型预测控制 介绍
1 介绍
1.1 概述
模型预测控制(Model Predictive Control,MPC)是一种基于模型的方法,它通过预测未来状态来优化控制策略。MPC 算法通常用于无人驾驶、机器人控制等领域。
kalman filter
1.2 发展历史
-
1970年代:MPC的早期概念开始形成,J. Richalet和A. Rault在法国提出了一种动态矩阵控制(Dynamic Matrix Control, DMC)算法,这是MPC的前身之一。
-
1980年代:MPC开始得到更广泛的关注和研究。在这一时期,Qin Shen和John MacGregor提出了模型算法控制(Model Algorithmic Control, MAC)。
-
1980年代末:随着计算机技术的发展,MPC开始在工业应用中得到实际应用,尤其是在化工和石油行业。
-
1990年代:MPC理论得到了进一步的发展,出现了多种不同的MPC算法,如有限时域控制(Finite Time Control)、无限时域控制(Infinite Time Control)等。
-
2000年代:MPC在多个领域得到应用,包括汽车、航空、能源等。算法的效率和鲁棒性也得到了显著提高。
-
2010年代至今:随着计算能力的进一步提升和优化算法的发展,MPC变得更加高效和灵活。它被应用于更广泛的领域,如自动驾驶汽车、机器人技术、生物过程控制等。
1.3 MPC 与 LQR
模型预测控制和线性二次调节器都是最优控制的表现,但优化成本的设置方案不同。
虽然模型预测控制器通常着眼于固定长度、通常是逐渐加权的误差函数集,但线性二次调节器会着眼于所有线性系统输入,并提供可减少整个频谱总误差的传递函数,从而平衡状态误差和输入频率。
由于这些根本差异,LQR 具有更好的全局稳定性能,但 MPC 通常具有更多的局部最优[?]和复杂的性能。
MPC 和LQR之间的主要区别在于 LQR 在整个时间窗口(范围)内进行优化,而 MPC 在后退时间窗口内进行优化,[ 4 ]并且 MPC 经常计算出一个新解,而 LQR 在整个时间范围内使用同一个(最优)解。因此,MPC 通常在比整个范围更小的时间窗口内解决优化问题,因此可能会得到次优解。但是,由于 MPC 不对线性做出任何假设,因此它可以处理硬约束以及非线性系统偏离其线性化工作点的迁移,这两者都是 LQR 的主要缺点。
这意味着 LQR 在远离稳定固定点时会变得很弱。MPC 可以在这些固定点之间绘制一条路径,但不能保证解决方案的收敛,尤其是当忽略了问题空间的凸性和复杂性时。
| 特性/方面 | MPC(模型预测控制) | LQR(线性二次调节器) |
|---|---|---|
| 基本方法 | 基于非线性模型的优化 | 基于线性状态空间模型 |
| 模型要求 | 需要系统模型 | 需要系统模型,且为线性 |
| 优化范围 | 预测未来路径并优化 | 优化未来某个时间点的成本 |
| 目标 | 最小化预测的轨迹与参考轨迹的差异 | 状态变量和控制输入的加权和最小化 |
| 控制结构 | 每个控制周期进行优化 | 求解代数黎卡提方程得到固定增益 |
| 实时性 | 需要足够的计算能力以实时优化 | 实时性较好,因为增益是预先计算的 |
| 适用性 | 适用于非线性和多变的系统 | 主要适用于线性系统或线性化后的非线性系统 |
| 鲁棒性 | 可以通过权重调整提高鲁棒性 | 鲁棒性较差,对模型的准确性要求较高 |
| 计算复杂度 | 较高,因为需要在每个控制周期进行优化 | 较低,因为增益是固定的,只需应用 |
| 优点 | 能够处理更复杂的系统和约束 | 控制结构简单,易于实现和理解 |
| 缺点 | 实现和计算可能较为复杂和耗时 | 可能无法处理强非线性和复杂约束 |
| 应用场景 | 汽车动力系统、飞行控制等 | 简单的电机控制、飞行器稳定性控制等 |
1.4 EKF 与 MPC 对比
| 对比项 | 扩展卡尔曼滤波 (EKF) | 模型预测控制 (MPC) |
|---|---|---|
| 定义 | 一种非线性系统状态估计的滤波技术 | 一种优化控制方法,用于预测和控制未来行为 |
| 应用场景 | 需要对系统状态进行估计时 | 需要在约束条件下进行最优控制时 |
| 处理问题类型 | 非线性系统的状态估计问题 | 多变量、多约束的最优控制问题 |
| 计算复杂度 | 相对较低,但每次迭代需要线性化处理 | 较高,需要解决优化问题 |
| 优势 | 实现相对简单,适用于实时系统 | 考虑未来预测,可以处理多约束问题 |
| 劣势 | 对于高度非线性系统可能不够准确 | 需要较长的计算时间,对实时性有影响 |
| 典型应用 | 飞行器导航、机器人定位 | 化工过程控制、汽车动力系统 |
1.5 经典控制器、预测控制器 和 重复控制器 比较
| 特性 | 经典控制器 | 预测控制器 (MPC) | 重复控制器 (Repetitive Control) |
|---|---|---|---|
| 代表算法 | PID控制器 | 模型预测控制 | 重复控制算法 |
| 应用场景 | 工业自动化、家用电器等 | 过程控制、汽车控制等 | 周期性干扰下的系统控制 |
| 优点 | - 简单易懂 - 实现容易 - 鲁棒性较好 | - 考虑未来预测 - 可以处理多变量和约束 - 优化性能 | - 对周期性干扰有良好的抑制效果 - 可以提高系统的稳定性和精度 |
| 缺点 | - 对系统模型要求不高 - 难以处理多变量和约束问题 | - 计算复杂度高 - 实时性要求较高 - 对模型准确性依赖大 | - 对非周期性干扰抑制效果有限 - 设计参数选择需要经验 |
| 适用性 | 适用于简单系统,或对控制性能要求不高的场合 | 适用于复杂系统,需要优化控制性能的场合 | 适用于存在周期性干扰的场合,需要高精度控制 |
| 设计复杂度 | 较低 | 较高 | 中等 |
| 鲁棒性 | 较好 | 一般 | 较好 |
| 实时性 | 好 | 取决于计算能力 | 好 |
| 可调整性 | 容易 | 较难,需要优化算法 | 中等 |
| 算法效率 | 高 | 低,需要快速优化算法 | 中等 |
| 代表应用 | 温度控制、速度控制等 | 化工过程、汽车动力系统等 | 磁盘驱动器定位、电机控制等 |
2 理解
stanford–MPC
由于文档内容较长,我将提供全文的翻译,但请注意,由于篇幅限制,翻译将尽可能简洁明了。
第一部分:概念
- 课程编号:EE392m - 2005年春季 Gorinevsky 控制工程
- 内容:
- 历史和工业应用资源:Joe Qin的工业MPC算法调查 - 链接
- 新兴应用
- 基于状态的 MPC - MPC的概念思想 - 最优控制综合
- 示例 - 汽车的横向控制
- 稳定性
- 第15讲:工业 MPC
MPC概念
- MPC = 模型预测控制 (Model Predictive Control)
- 也称为:
- DMC = 动态矩阵控制 (Dynamical Matrix Control)
- GPC = 广义预测控制 (Generalized Predictive Control)
- RHC = 滚动时域控制 (Receding Horizon Control)
- 控制算法基于:
- 每一步都通过数值求解优化问题
- 约束优化 - 通常是二次规划(QP)或线性规划(LP)
- 递归地平线控制
- 实施需要更多细节
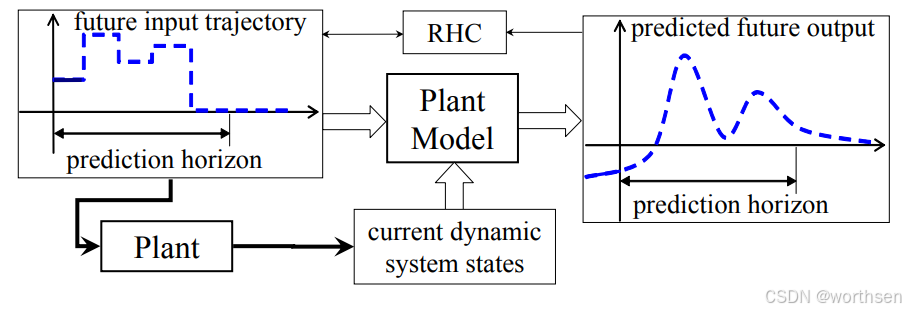
滚动时域控制 (Receding Horizon Control) RHC
-
滚动时域控制概念
-
每个时间步,通过求解开环优化问题来计算预测时域的控制
-
应用计算出的控制序列的第一个值
-
在下一个时间步,获取系统状态并重新计算
当前 MPC 使用情况
- 在现有的多变量控制应用中使用广泛
- 许多新的高级多变量控制应用的首选技术
- 成功依赖于计算能力的提高
- 拥有许多重要的实际优势
MPC 优势
- 基于易于理解的概念,公式明确
- 明确处理约束
- 显式使用模型
- 易于理解的调参参数:
- 预测时域
- 优化问题设置
- 开发时间比竞争的高级控制方法短得多
- 更易于维护:更改模型或规格不需要完全重新设计,有时可以即时完成
历史
- 第一个实际应用:
- DMC - 动态矩阵控制,20世纪70年代初在Shell Oil公司
- Cutler后来创立了Dynamic Matrix Control公司
- 许多成功的工业应用
- 理论(稳定性证明等)落后10-20年
- 工业MPC的优秀资源 - Joe Qin的工业MPC算法调查 - 历史和公式化 - 链接
新兴MPC应用
-
非线性MPC
- 只需要一个可计算的模型(仿真)
- 非线性规划(NLP)优化
-
混合MPC
- 离散和参数变量
- 动态和离散模式变化的组合
- 混合整数优化(MILP, MIQP)
-
发动机控制
-
大规模操作控制问题
- 运营管理(供应链控制)
- 活动控制
-
车辆路径规划与控制
- 非线性车辆模型
- 世界模型
- 递归时域预览
-
航天器与空间站对接
- 可见性圆锥约束
- 燃料最优化
-
水下车辆导航
-
导弹制导
基于状态的控制综合
- 为了更清晰的理解,考虑单输入系统
x ( t + 1 ) = A x ( t ) + B u ( t ) y ( t ) = C x ( t ) \begin{align} x(t+1) & = A x(t) + B u(t) \\ y(t) & = C x(t) \end{align} x(t+1)y(t)=Ax(t)+Bu(t)=Cx(t)
- 无限时域最优控制
∑ τ = t + 1 ∞ ( y ( τ ) ) 2 + r ( u ( τ ) − u ( τ − 1 ) ) 2 → min \sum_{\tau=t+1}^{\infty} (y(\tau))^2 + r(u(\tau) - u(\tau-1))^2 \rightarrow \min ∑τ=t+1∞(y(τ))2+r(u(τ)−u(τ−1))2→min
subject to: ∣ u ( τ ) ∣ ≤ u 0 \text{subject to: } |u(\tau)| \leq u_0 subject to: ∣u(τ)∣≤u0
- 解决方案 = 最优控制综合
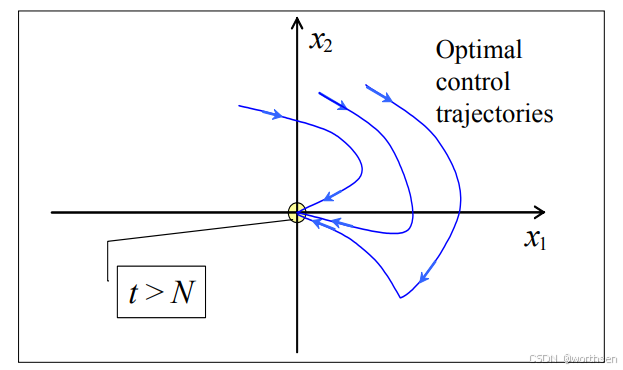
基于状态的 MPC
- 最优控制轨迹收敛于 (0,0):
- 如果N很大,可以忽略 t > N 时的问题部分
- 无限时域的最优控制 ≈ N 步时域的最优控制
- 递归时域控制;N 步最优
J = ∑ τ = t + 1 t + N ( y ( τ ) ) 2 + r ( u ( τ ) − u ( τ − 1 ) ) 2 → min J = \sum_{\tau=t+1}^{t+N} (y(\tau))^2 + r(u(\tau) - u(\tau-1))^2 \rightarrow \min J=∑τ=t+1t+N(y(τ))2+r(u(τ)−u(τ−1))2→min
subject to: ∣ u ( τ ) ∣ ≤ u 0 , \text{subject to: } |u(\tau)| \leq u_0, subject to: ∣u(τ)∣≤u0,
x ( t + 1 ) = A x ( t ) + B u ( t ) x(t+1) = A x(t) + B u(t) x(t+1)=Ax(t)+Bu(t)
y ( t ) = C x ( t ) y(t) = C x(t) y(t)=Cx(t)
- 解决方案 ≈ \approx ≈ 最优控制综合
x ( t ) → [ MPC Problem Solver ] → u ( t ) x(t) \rightarrow [\text{MPC Problem Solver}] \rightarrow u(t) x(t)→[MPC Problem Solver]→u(t)
预测模型
- 预测系统模型
Y = G x + H U + F u Y = G x + H U + F u Y=Gx+HU+Fu (初始条件响应 + 控制响应)
Y = [ y ( t + 1 ) ⋮ y ( t + N ) ] 预测输出 U = [ u ( t + 1 ) ⋮ u ( t + N ) ] 未来控制输入 x = x ( t ) 当前状态,初始条件 u = u ( t ) → 在前一步计算 \begin{array}{lcl} Y & = & \left[ \begin{array}{c} y(t+1) \\ \vdots \\ y(t+N) \end{array} \right] \text{ 预测输出 } \\ U & = & \left[ \begin{array}{c} u(t+1) \\ \vdots \\ u(t+N) \end{array} \right] \text{ 未来控制输入 } \\ x & = & x(t) \text{ 当前状态,初始条件 } \\ u & = & u(t) \rightarrow \text{ 在前一步计算} \end{array} YUxu==== y(t+1)⋮y(t+N) 预测输出 u(t+1)⋮u(t+N) 未来控制输入 x(t) 当前状态,初始条件 u(t)→ 在前一步计算
- 模型矩阵
G = [ C A ⋮ C A n ] H = [ 0 0 … 0 C B 0 … 0 ⋮ ⋮ ⋱ ⋮ C A N − 2 B C A N − 3 B … 0 ] = [ h ( 1 ) 0 … 0 h ( 2 ) h ( 1 ) … 0 ⋮ ⋮ ⋱ ⋮ h ( N ) h ( N − 1 ) … h ( 1 ) ] F = [ h ( 2 ) h ( 3 ) ⋮ h ( N + 1 ) ] \begin{array}{lcl} G & = & \left[ \begin{array}{c} C A \\ \vdots \\ C A^n \end{array} \right] \\ H & = & \left[ \begin{array}{ccccc} 0 & 0 & \ldots & 0 \\ C B & 0 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ C A^{N-2} B & C A^{N-3} B & \ldots & 0 \end{array} \right] = \left[ \begin{array}{ccccc} h(1) & 0 & \ldots & 0 \\ h(2) & h(1) & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ h(N) & h(N-1) & \ldots & h(1) \end{array} \right] \\ F & = & \left[ \begin{array}{c} h(2) \\ h(3) \\ \vdots \\ h(N+1) \end{array} \right] \end{array} GHF=== CA⋮CAn 0CB⋮CAN−2B00⋮CAN−3B……⋱…00⋮0 = h(1)h(2)⋮h(N)0h(1)⋮h(N−1)……⋱…00⋮h(1) h(2)h(3)⋮h(N+1)
计算时间线
在前一步计算:
u
(
t
)
u(t)
u(t)。
基于 x(t) 计算控制 u(t+1) ,并应用它。
- 假设控制 u 在同一瞬时 t 被应用,状态 x 被采样。
- 整个采样间隔都可用于计算 u
MPC优化问题设置
-
MPC优化问题
J = Y T Y + r U T D T D U → min subject to: ∣ U ∣ ≤ u 0 , Y = G x + H U + F u \begin{align*} J =& Y^T Y + r U^T D^T D U \rightarrow \min \\ \text{subject to: } |U| \leq& u_0, \\ Y =& G x + H U + F u \end{align*} J=subject to: ∣U∣≤Y=YTY+rUTDTDU→minu0,Gx+HU+Fu
D = [ 1 − 1 … 0 0 1 … 0 ⋮ ⋮ ⋱ ⋮ 0 0 … 0 ] D = \left[ \begin{array}{cccc} 1 & -1 & \ldots & 0 \\ 0 & 1 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & 0 \end{array} \right] D= 10⋮0−11⋮0……⋱…00⋮0 -
这是一个二次规划问题(QP problem)。
-
解决方案
x ( t ) → [ MPC Problem, QP Solver ] → U → u ( t + 1 ) = U ( 1 ) x(t) \rightarrow [\text{MPC Problem, QP Solver}] \rightarrow U \rightarrow u(t+1) = U(1) x(t)→[MPC Problem, QP Solver]→U→u(t+1)=U(1)
QP解决方案
-
QP问题:
U = U ( t ) 预测的控制序列 A U ≤ b J = 1 2 U T Q U + f T U → min \begin{array}{ll} U = U(t) \quad \text{预测的控制序列} \\ A U \leq b \\ J = \frac{1}{2} U^T Q U + f^T U \rightarrow \min & \end{array} U=U(t)预测的控制序列AU≤bJ=21UTQU+fTU→min
Q = r D T D + H T H A = [ I − I ] b = [ 1 ⋮ 1 ] ⋅ u 0 f = H T ( G x + F u ) \begin{array}{ll} Q = r D^T D + H^T H & A = \left[ \begin{array}{c} I \\ -I \end{array} \right] \quad b = \left[ \begin{array}{c} 1 \\ \vdots \\ 1 \end{array} \right] \cdot u_0 \\ f = H^T(G x + F u) & \end{array} Q=rDTD+HTHf=HT(Gx+Fu)A=[I−I]b= 1⋮1 ⋅u0 -
可以使用标准QP代码
线性MPC
-
非线性由约束条件引起
-
如果约束条件不活跃,QP问题的解是
U = Q − 1 f u = l T U U = Q^{-1} f \quad u = l^T U U=Q−1fu=lTU
l = [ 1 0 ⋮ 0 ] l = \left[ \begin{array}{c} 1 \\ 0 \\ \vdots \\ 0 \end{array} \right] l= 10⋮0 -
这是线性状态反馈
u ( t + 1 ) = l T ( r D T D + H T H ) − 1 H T ( G x ( t ) + F u ( t ) ) u = z − 1 K x + z − 1 S u K = l T ( r D T D + H T H ) − 1 H T G S = l T ( r D T D + H T H ) − 1 H T F \begin{array}{c} u(t+1) = l^T \left( r D^T D + H^T H \right)^{-1} H^T (G x(t) + F u(t)) \\ u = z^{-1} K x + z^{-1} S u \\ K = l^T \left( r D^T {D + H^T H} \right)^{-1} H^T G \\ S = l^T \left( r {D^T D} + H^T H \right)^{-1} H^T F \end{array} u(t+1)=lT(rDTD+HTH)−1HT(Gx(t)+Fu(t))u=z−1Kx+z−1SuK=lT(rDTD+HTH)−1HTGS=lT(rDTD+HTH)−1HTF -
可以作为线性系统进行分析,例如,检查特征值
u = z − 1 1 − S z − 1 K x u = \frac{z^{-1}}{1 - S z^{-1}} K x u=1−Sz−1z−1Kx
z x = A x + B u z x = A x + B u zx=Ax+Bu
非线性 MPC 稳定性
- 定理 - 来自Bemporad等人(1994)
考虑一个带有约束条件的线性规划的 MPC 算法。假设存在一个终端约束。
x ( t + N ) = 0 对于预测状态 x 和 x(t+N) = 0 \text{ 对于预测状态 } x \text{ 和} x(t+N)=0 对于预测状态 x 和
u ( t + N ) = 0 对于计算出的未来控制 u u(t+N) = 0 \text{ 对于计算出的未来控制 } u u(t+N)=0 对于计算出的未来控制 u
如果优化问题是在时间 t 可行的,那么坐标原点是稳定的。
证明:
使用性能指标 J 作为李雅普诺夫函数。它沿着在时间 t 计算的有限可行轨迹减少。这个轨迹对于 MPC 算法来说是次优的,因此 J 减少得更快。
MPC稳定性
- 分析在实践中可能有用
- 理论表明终端约束是好的
- MPC稳定性公式
(Mayne等人,Automatica,2000) - 终端等式约束
- 终端代价函数
- 双模式控制 - 无限时域
- 终端约束集
- 增加可行性区域
- 终端代价和约束集
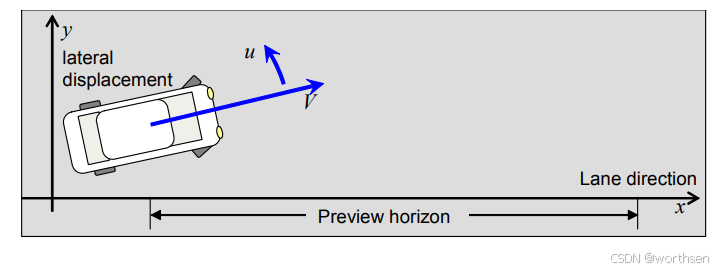
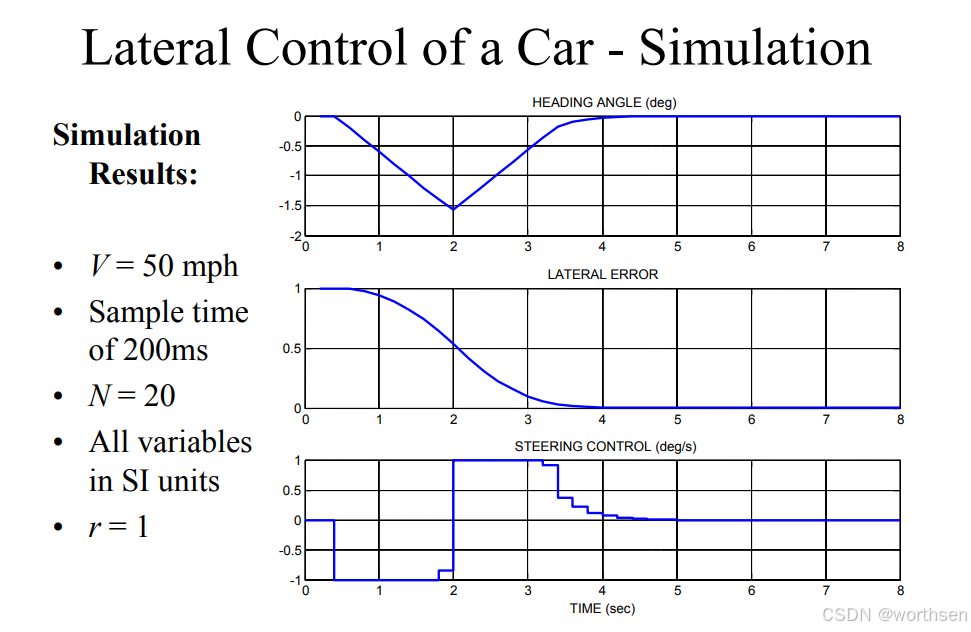
示例:汽车的横向控制
- 预测控制 - MacAdam的驾驶员模型(1980)
- 考虑预测控制设计
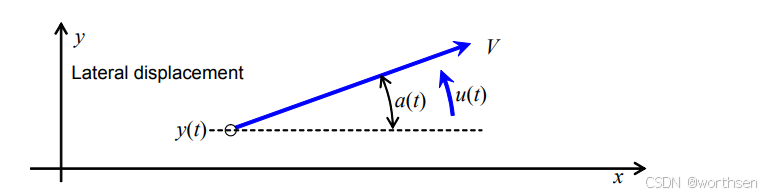
- 以速度 V 行驶的汽车的简单运动学模型
x ˙ = V cos a y ˙ = V sin a 横向位移 a ˙ = u 转向 \begin{align*} \dot{x} & = V \cos a \\ \dot{y} & = V \sin a \quad \text{横向位移} \\ \dot{a} & = u \quad \text{转向} \end{align*} x˙y˙a˙=Vcosa=Vsina横向位移=u转向
汽车的横向控制 - 模型
-
假设是直线车道 - 跟踪直线
-
线性化系统:假设 a < < 1 a << 1 a<<1
sin a ≈ a y ˙ = V a cos a ≈ 1 a ˙ = u \begin{array}{ll} \sin a \approx a & \dot{y} = V a \\ \cos a \approx 1 & \dot{a} = u \end{array} sina≈acosa≈1y˙=Vaa˙=u -
采样时间方程(采样时间 T s T_s Ts )
a ( t + 1 ) = a ( t ) + u ( t ) T s y ( t + 1 ) = y ( t ) + a ( t ) V T s + u ( t ) ⋅ 0.5 V T s 2 \begin{align*} a(t+1) &= a(t) + u(t) T_s \\ y(t+1) &= y(t) + a(t) V T_s + u(t) \cdot 0.5 V T_s^2 \end{align*} a(t+1)y(t+1)=a(t)+u(t)Ts=y(t)+a(t)VTs+u(t)⋅0.5VTs2
汽车横向控制 - MPC
状态空间系统:
x
(
t
+
1
)
=
A
x
(
t
)
+
B
u
(
t
)
x(t+1) = A x(t) + B u(t)
x(t+1)=Ax(t)+Bu(t)
x
(
t
)
=
[
a
(
t
)
y
(
t
)
]
A
=
[
1
0
V
T
s
1
]
,
B
=
[
T
s
0.5
V
T
s
2
]
x(t) = \begin{bmatrix} a(t) \\ y(t) \end{bmatrix} \quad A = \begin{bmatrix} 1 & 0 \\ V T_{s} & 1 \end{bmatrix}, \quad B = \begin{bmatrix} T_{s} \\ 0.5 V T_{s}^{2} \end{bmatrix}
x(t)=[a(t)y(t)]A=[1VTs01],B=[Ts0.5VTs2]
观测 y ( t ) = C x ( t ) y(t) = Cx(t) y(t)=Cx(t), C = [ 0 1 ] C = \begin{bmatrix} 0 & 1 \end{bmatrix} C=[01]
-
构建预测模型
Y = G x + H U + F u Y = G x + H U + F u Y=Gx+HU+Fu -
MPC优化问题
J = ( G x + H U + F u ) T ( G x + H U + F u ) + r U T D T D U → min J = (G x + H U + F u)^{T}(G x + H U + F u) + r U^{T} D^{T} D U \rightarrow \min J=(Gx+HU+Fu)T(Gx+HU+Fu)+rUTDTDU→min
约束条件: ∣ U ∣ ≤ u 0 |U| \leq u_{0} ∣U∣≤u0 -
解决方案
x ( t ) → [ M P C Q P ] → U → u ( t + 1 ) = U ( 1 ) x(t) \rightarrow [MPC \quad QP] \rightarrow U \rightarrow u(t+1) = U(1) x(t)→[MPCQP]→U→u(t+1)=U(1)
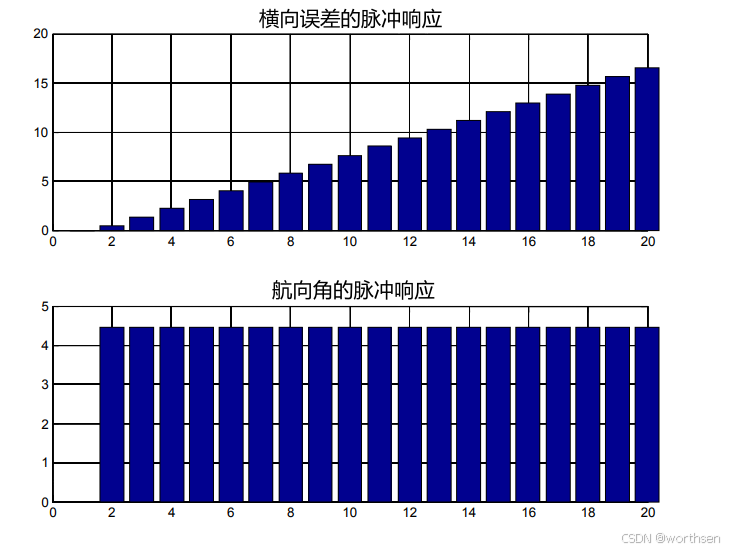
脉冲响应
以下是对提供的英文段落的中文翻译:
控制设计问题
- 仍有几个重要问题未解决
- 这些问题在这个模拟中并不明显
- 将在第15讲(MPC,第二部分)中讨论
- 并非所有状态都可用
- 稳态误差
- 需要积分器反馈
- 大角度偏差
- 线性化模型的不足
- 引入软约束
do-mpc: Basics of model predictive control
do-mpc: Basics of model predictive control
https://www.do-mpc.com/en/latest/index.html
介绍
do-mpc是一个全面的开源工具箱,用于稳健模型预测控制 (MPC) 和移动时域估计 (MHE)。do -mpc能够有效地制定和解决非线性系统的控制和估计问题,包括处理不确定性和时间离散化的工具。do -mpc的模块化结构包含模拟、估计和控制组件,可以轻松扩展和组合以适应许多不同的应用。
模型预测控制基础
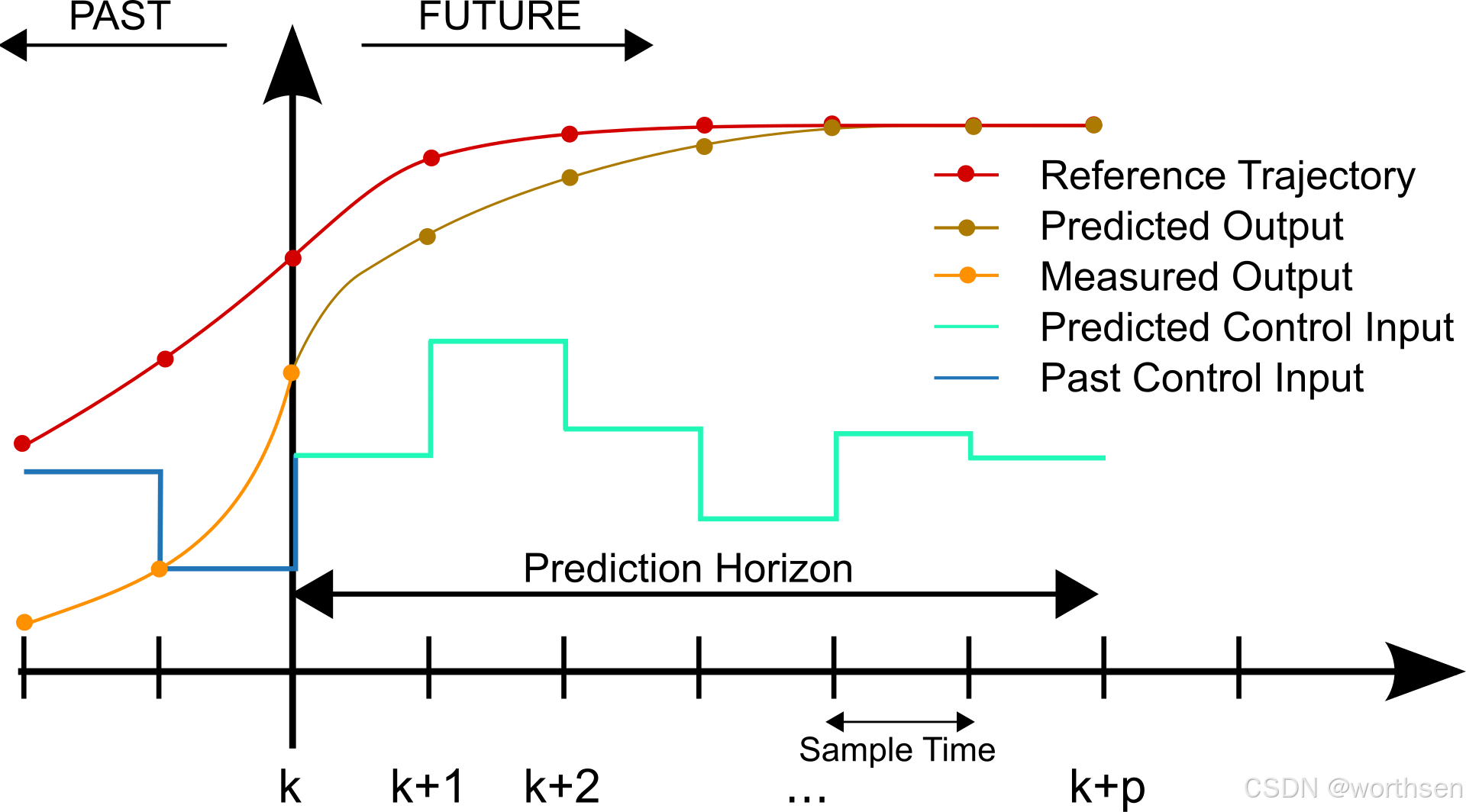
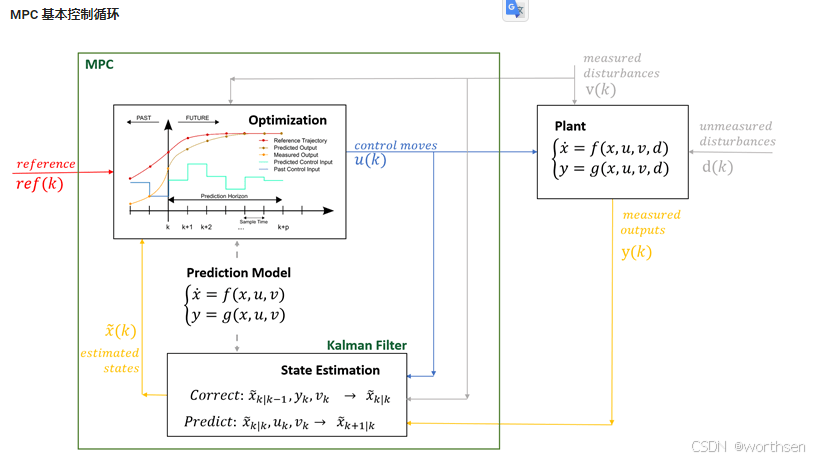
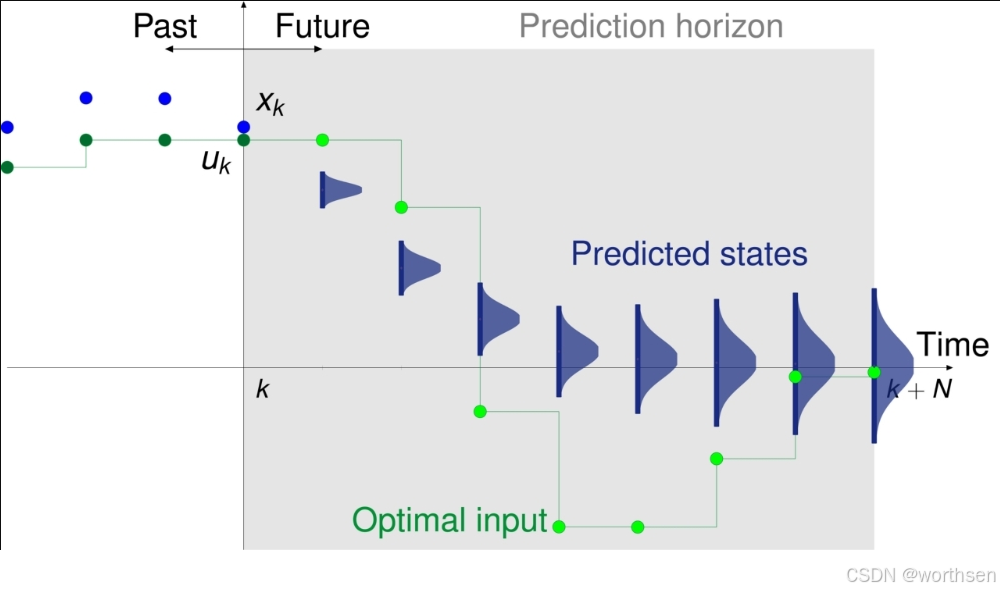
模型预测控制 (MPC)是一种控制方案,其中使用模型来预测系统在有限时间窗口(即时间范围)内的未来行为。基于这些预测和系统当前测量/估计的状态,计算出相对于定义的控制目标并受系统约束的最佳控制输入。在一定时间间隔后,使用移动时间范围重复测量、估计和计算过程。这就是该方法也称为滚动时间范围控制 (RHC) 的原因。
与传统的反应控制方法(例如 PID 等)相比,MPC 的主要优势在于
- 主动控制行动:控制器预测未来的干扰、设定点等。
- 非线性控制:MPC 可以明确考虑非线性系统,无需线性化
- 任意控制目标:传统设定点跟踪和调节或经济 MPC
- 约束公式:明确考虑物理、安全或操作系统约束
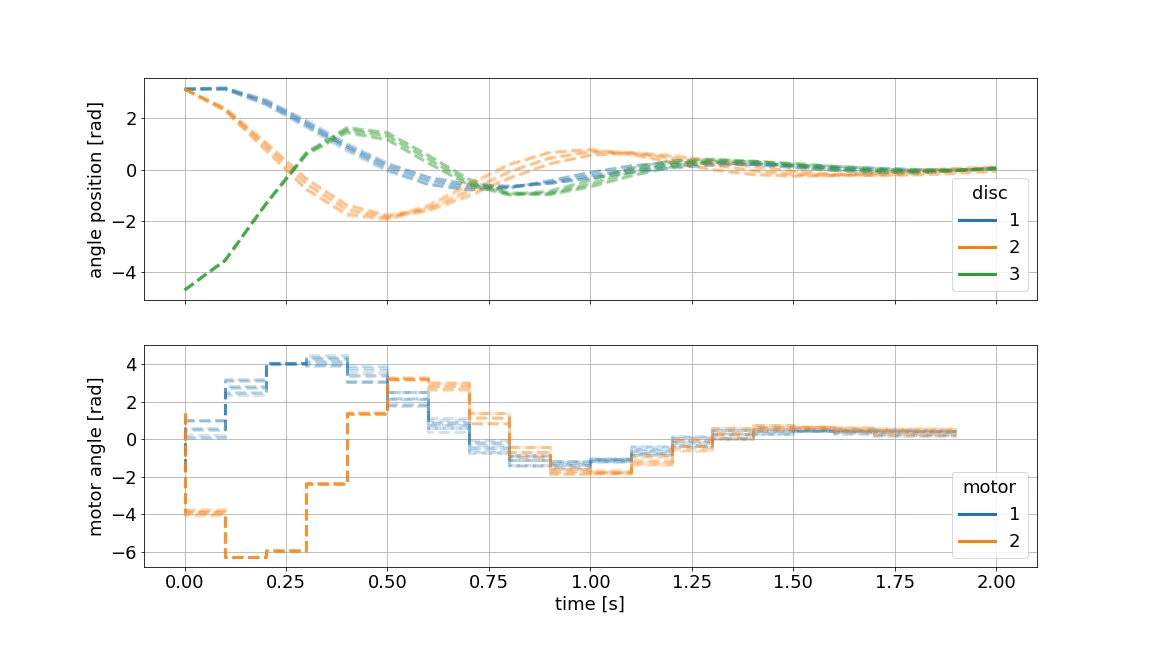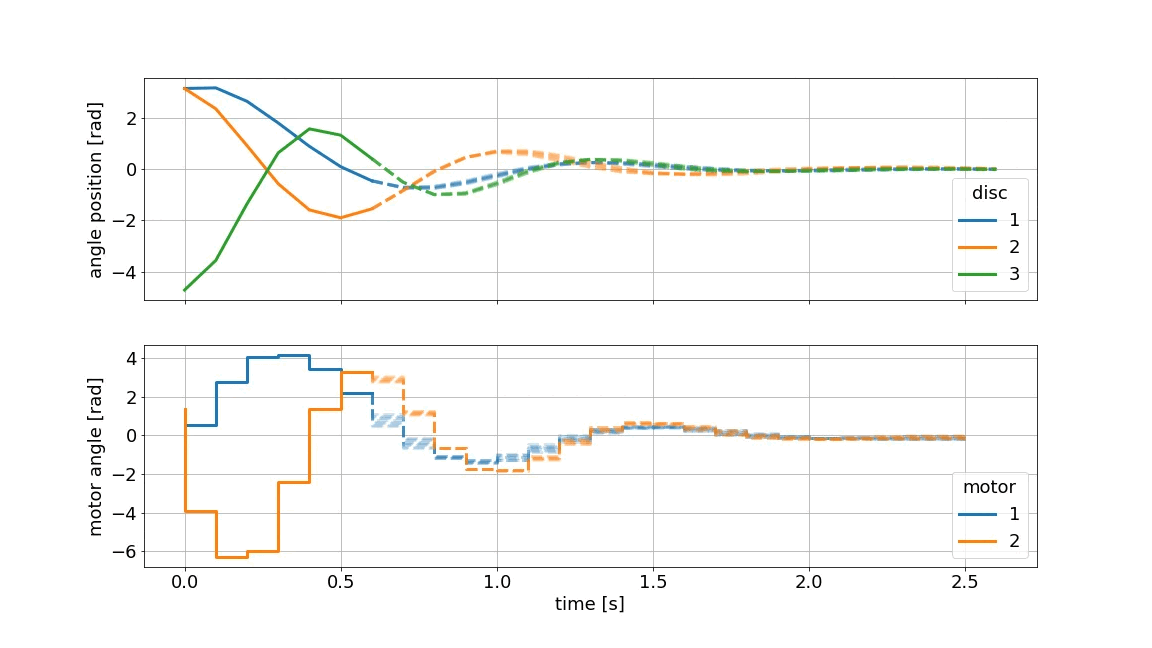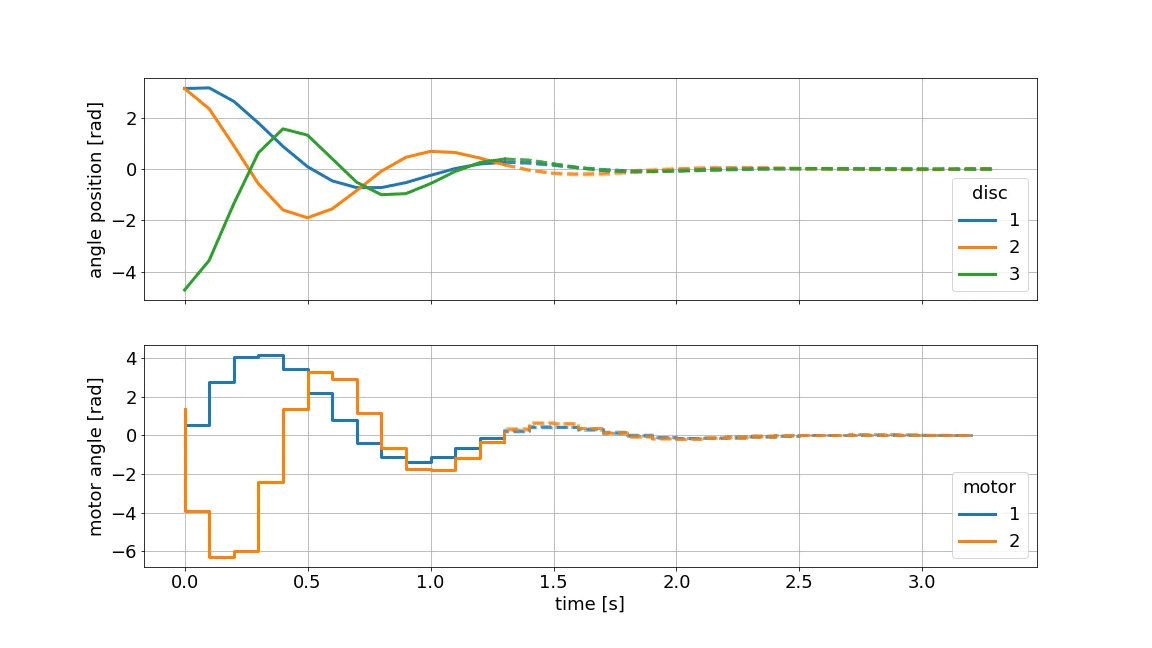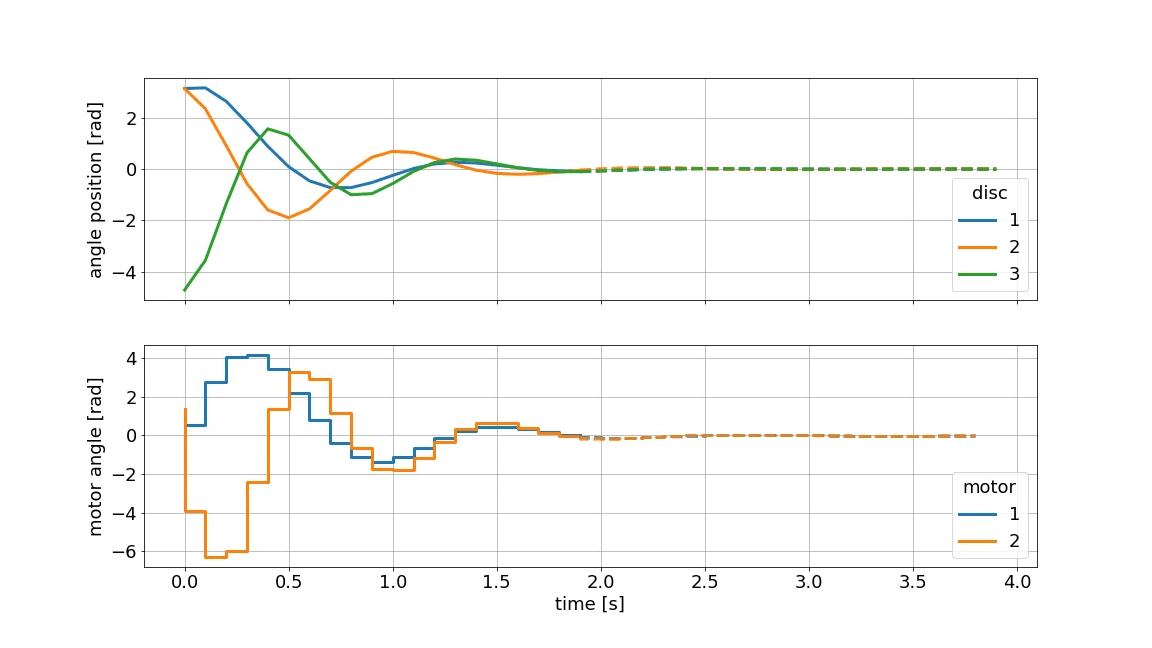
上图直观地展示了 MPC 原理。虚线表示当前预测,实线表示实际值。该图是使用do-mpc的固有绘图功能生成的。
接下来,我们将介绍可以考虑的模型类型。然后,介绍(基本)最优控制问题 (OCP) 。最后,解释多阶段 NMPC ,即do-mpc中使用的稳健 NMPC 方法。
系统
系统模型在 MPC 中起着核心作用。do-mpc可以实现连续和离散时间非线性和不确定系统的最优控制。对于连续情况,系统模型定义为
x
˙
(
t
)
=
f
(
x
(
t
)
,
u
(
t
)
,
z
(
t
)
,
p
(
t
)
,
p
tv
(
t
)
)
,
y
(
t
)
=
h
(
x
(
t
)
,
u
(
t
)
,
z
(
t
)
,
p
(
t
)
,
p
tv
(
t
)
)
,
\begin{array}{l} \dot{x}(t) = f(x(t), u(t), z(t), p(t), p_{\text{tv}}(t)), \\ y(t) = h(x(t), u(t), z(t), p(t), p_{\text{tv}}(t)), \end{array}
x˙(t)=f(x(t),u(t),z(t),p(t),ptv(t)),y(t)=h(x(t),u(t),z(t),p(t),ptv(t)),
对于离散时间的情况:
x
k
+
1
=
f
(
x
k
,
u
k
,
z
k
,
p
k
,
p
tv
,
k
)
,
y
k
=
h
(
x
k
,
u
k
,
z
k
,
p
k
,
p
tv
,
k
)
.
\begin{align*} x_{k+1} & = f(x_k, u_k, z_k, p_k, p_{\text{tv}, k}), \\ y_k & = h(x_k, u_k, z_k, p_k, p_{\text{tv}, k}). \end{align*}
xk+1yk=f(xk,uk,zk,pk,ptv,k),=h(xk,uk,zk,pk,ptv,k).
系统状态由下式给出: x ( t ) , x k x(t), x_{k} x(t),xk,控制输入为 u ( t ) , u k u(t), u_{k} u(t),uk,代数状态 z ( t ) , z k z(t), z_{k} z(t),zk,(不确定)参数 p ( t ) , p k p(t), p_{k} p(t),pk,随时间变化(但已知)的参数 p tv ( t ) , p tv , k p_{\text{tv}}(t), p_{\text{tv},k} ptv(t),ptv,k 并测量 y ( t ) , y k y(t), y_{k} y(t),yk 分别表示为 t t t 对于连续系统,时间步长为 k k k 对于离散系统。
模型预测控制
对于连续系统的情况,尝试直接解决OCP在一般情况下在计算上是难以解决的,因为它是一个无限维问题。do-mpc使用完全离散化方法,即正交配点,来离散化OCP。这意味着,连续系统和离散系统的OCP都会产生类似的离散OCP。
对于MPC的应用,需要了解系统的当前状态。一般来说,测量 y k y_{k} yk 不包含整个状态向量,这意味着状态估计 x ^ k \hat{x}_{k} x^k 需要计算。状态估计可以通过移动范围估计等方法得出。
OCP由以下公式给出:
min
x
0
:
N
+
1
,
u
0
:
N
,
z
0
:
N
m
(
x
N
+
1
)
+
∑
k
=
0
N
l
(
x
k
,
z
k
,
u
k
,
p
k
,
p
tv
,
k
)
subject to:
x
0
=
x
^
0
,
x
k
+
1
=
f
(
x
k
,
u
k
,
p
k
,
p
tv
,
k
)
,
∀
k
=
0
,
…
,
N
,
g
(
x
k
,
u
k
,
p
k
,
p
tv
,
k
)
≤
0
,
∀
k
=
0
,
…
,
N
,
x
lb
≤
x
k
≤
x
ub
,
∀
k
=
0
,
…
,
N
,
u
lb
≤
u
k
≤
u
ub
,
∀
k
=
0
,
…
,
N
,
z
lb
≤
z
k
≤
z
ub
,
∀
k
=
0
,
…
,
N
,
g
terminal
(
x
N
+
1
)
≤
0.
\begin{split} & \min_{\mathbf{x}_{0:N+1}, \mathbf{u}_{0:N}, \mathbf{z}_{0:N}} \quad m(x_{N+1}) + \sum_{k=0}^{N} l(x_k, z_k, u_k, p_k, p_{\text{tv},k}) \\ & \text{subject to:} \\ & \quad x_0 = \hat{x}_0, \\ & \quad x_{k+1} = f(x_k, u_k, p_k, p_{\text{tv},k}), \quad \forall k=0, \dots, N, \\ & \quad g(x_k, u_k, p_k, p_{\text{tv},k}) \leq 0, \quad \forall k=0, \dots, N, \\ & \quad x_{\text{lb}} \leq x_k \leq x_{\text{ub}}, \quad \forall k=0, \dots, N, \\ & \quad u_{\text{lb}} \leq u_k \leq u_{\text{ub}}, \quad \forall k=0, \dots, N, \\ & \quad z_{\text{lb}} \leq z_k \leq z_{\text{ub}}, \quad \forall k=0, \dots, N, \\ & \quad g_{\text{terminal}}(x_{N+1}) \leq 0. \end{split}
x0:N+1,u0:N,z0:Nminm(xN+1)+k=0∑Nl(xk,zk,uk,pk,ptv,k)subject to:x0=x^0,xk+1=f(xk,uk,pk,ptv,k),∀k=0,…,N,g(xk,uk,pk,ptv,k)≤0,∀k=0,…,N,xlb≤xk≤xub,∀k=0,…,N,ulb≤uk≤uub,∀k=0,…,N,zlb≤zk≤zub,∀k=0,…,N,gterminal(xN+1)≤0.
其中 N N N 是预测范围, x ^ 0 \hat{x}_0 x^0 是当前状态估计值,可以是测量得到的(状态反馈)或基于不完整测量估计得到的( y k y_k yk)。请注意,我们引入了粗体字母表示法,例如 x 0 : N + 1 = [ x 0 , x 1 , … , x N + 1 ] T \mathbf{x}_{0:N+1} = [x_0, x_1, \dots, x_{N+1}]^T x0:N+1=[x0,x1,…,xN+1]T 表示序列。
do-mpc 允许设置状态的上限和下限 x lb , x ub x_{\text{lb}}, x_{\text{ub}} xlb,xub 、输入 u lb , u ub u_{\text{lb}}, u_{\text{ub}} ulb,uub 以及代数状态 z lb , z ub z_{\text{lb}}, z_{\text{ub}} zlb,zub 。终端约束可以通过 g terminal ( ⋅ ) g_{\text{terminal}}(\cdot) gterminal(⋅) 强制执行,并且一般非线性约束可以定义为 g ( ⋅ ) g(\cdot) g(⋅) ,也可以实现为软约束。目标函数由两部分组成,Mayer项 m ( ⋅ ) m(\cdot) m(⋅) 给出了终端状态的成本,而拉格朗日项 l ( ⋅ ) l(\cdot) l(⋅) 代表了每个阶段 k k k 的成本。
这个公式是OCP的基本公式,通过do-mpc求解。在下一节中,我们将解释do-mpc如何考虑不确定性以实现鲁棒控制。
稳健的多阶段 NMPC
do-mpc的主要特征之一是鲁棒控制,即在存在不确定性的情况下,控制动作满足系统约束。具体来说,我们应用了下文描述的多阶段方法。
一般描述
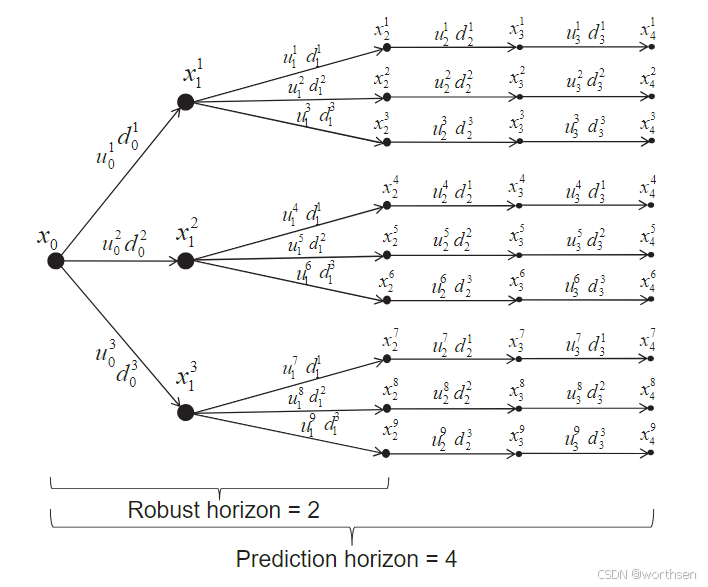
多阶段方法的基本思想是考虑各种场景,其中场景由视界内每个控制时刻所有不确定参数的一种可能实现定义。所有考虑的离散场景系列可以表示为树结构,称为场景树:
其中一个场景是从左侧根节点到右侧叶节点的一条路径,例如第一个场景的状态演变
S
4
S_{4}
S4 将是:
x
0
→
x
1
2
→
x
2
4
→
⋯
→
x
5
4
x_{0} \rightarrow x_{1}^{2} \rightarrow x_{2}^{4} \rightarrow \cdots \rightarrow x_{5}^{4}
x0→x12→x24→⋯→x54
在每个时刻,根节点的MPC问题
x
0
x_{0}
x0 解决了这个问题,同时明确考虑了未来演化的不确定性和未来决策的存在,这可以利用沿分支演化过程中获得的信息。通过这种设计,在开环优化问题中考虑了反馈信息,从而降低了多阶段方法的保守性。考虑反馈信息也意味着决策
u
u
u 从同一节点分支出来的分支需要相同,因为它们基于相同的信息,例如
u
1
4
=
u
1
5
=
u
1
6
u_{1}^{4} = u_{1}^{5} = u_{1}^{6}
u14=u15=u16。
多阶段设置中的离散化/离散系统的系统方程由下式给出:
x
k
+
1
j
=
f
(
x
k
p
(
j
)
,
u
k
j
,
z
k
p
(
j
)
,
p
k
r
(
j
)
,
p
tv
,
k
)
x_{k+1}^{j} = f(x_{k}^{p(j)}, u_{k}^{j}, z_{k}^{p(j)}, p_{k}^{r(j)}, p_{\text{tv},k})
xk+1j=f(xkp(j),ukj,zkp(j),pkr(j),ptv,k)
其中函数 p ( j ) p(j) p(j) 通过 x k p ( j ) x_{k}^{p(j)} xkp(j) 引用父状态,并且考虑的不确定性的实现由 r ( j ) r(j) r(j) 通过 d k r ( j ) d_{k}^{r(j)} dkr(j) 给出。所有出现的指数/指标对的集合 ( j , k ) (j,k) (j,k) 表示为 I I I。
稳健前景
由于在多阶段方法中,不确定性被建模为离散场景的集合,因此每个节点都会分支为 ∏ i = 1 n P v i \prod_{i=1}^{n_{\text{P}}} v_{i} ∏i=1nPvi 新的场景,其中 n P n_{\text{P}} nP 是参数的数量, v i v_{i} vi 是考虑的明确值的数量对于第 i i i 个参数。这导致场景相对于时域呈指数增长。为了保持多阶段方法的计算可处理性,引入了稳健时域 N robust N_{\text{robust}} Nrobust,这可以视为一个调整参数。然后分支仅适用于前 N robust N_{\text{robust}} Nrobust 步,而不确定参数的值在最后的 N − N robust N - N_{\text{robust}} N−Nrobust 步中保持不变。考虑的场景数量由以下公式给出:
N s = ( ∏ i = 1 n p v i ) N robust N_{\text{s}} = \left( \prod_{i=1}^{n_{\text{p}}} v_{i} \right)^{N_{\text{robust}}} Ns=(∏i=1npvi)Nrobust
这导致如果将分支应用到预测范围,上述情景树的情景将是 N s = 9 N_{\text{s}} = 9 Ns=9 个情景,而不是243个情景。
如果不确定性 p p p 未知但随时间恒定, N robust = 1 N_{\text{robust}} = 1 Nrobust=1 是建议的选择。在这种情况下,场景树的分支只需要在第一个时间点进行(因为不确定性是恒定的),并且计算负荷保持最小。
数学公式
多阶段方法的MPC问题公式如下:
min
x
0
j
,
u
0
j
,
z
k
j
∨
(
j
,
k
)
∈
I
∑
j
=
1
N
s
ω
i
J
j
(
x
0
:
N
+
1
j
,
u
0
:
N
j
,
z
0
:
N
j
)
\min\limits_{x_{0}^{j},u_{0}^{j},z_{k}^{j}\vee(j,k)\in I} \sum\limits_{j=1}^{N_{s}} \omega_{i} J_{j}(x_{0:N+1}^{j},u_{0:N}^{j},z_{0:N}^{j})
x0j,u0j,zkj∨(j,k)∈Iminj=1∑NsωiJj(x0:N+1j,u0:Nj,z0:Nj)
subject to: x 0 = x ^ 0 \text{subject to:}\quad x_{0} = \hat{x}_{0} subject to:x0=x^0
x k + 1 j = f ( x k p ( j ) , u k j , z k p ( j ) , p k r ( j ) , p t v , k ) ∀ ( j , k ) ∈ I u k i = u k j if x k p ( i ) = x k p ( j ) , ∀ ( i , k ) , ( j , k ) ∈ I g ( x k p ( j ) , u k j , z k p ( j ) , p k r ( j ) , p t v , k ) ≤ 0 ∀ ( j , k ) ∈ I x l b ≤ x k j ≤ x u b ∀ ( j , k ) ∈ I u l b ≤ u k j ≤ u u b ∀ ( j , k ) ∈ I z l b ≤ z k j ≤ z u b ∀ ( j , k ) ∈ I g t e r m i n a l ( x N j , z N j ) ≤ 0 ∀ ( j , N ) ∈ I \begin{align*} & x_{k+1}^{j} = f(x_{k}^{p(j)},u_{k}^{j},z_{k}^{p(j)},p_{k}^{r(j)},p_{tv,k}) \quad \forall(j,k) \in I\\ & u_{k}^{i} = u_{k}^{j} \quad \text{if } x_{k}^{p(i)} = x_{k}^{p(j)}, \quad \forall(i,k),(j,k) \in I\\ & g(x_{k}^{p(j)},u_{k}^{j},z_{k}^{p(j)},p_{k}^{r(j)},p_{ tv,k}) \leq 0 \quad \forall(j,k) \in I\\ & x_{lb} \leq x_{k}^{j} \leq x_{ub} \quad \forall(j,k) \in I\\ & u_{lb} \leq u_{k}^{j} \leq u_{ub} \quad \forall(j,k) \in I\\ & z_{lb} \leq z_{k}^{j} \leq z_{ub} \quad \forall(j,k) \in I\\ & g_{terminal}(x_{N}^{j},z_{N}^{j}) \leq 0 \quad \forall(j,N) \in I \end{align*} xk+1j=f(xkp(j),ukj,zkp(j),pkr(j),ptv,k)∀(j,k)∈Iuki=ukjif xkp(i)=xkp(j),∀(i,k),(j,k)∈Ig(xkp(j),ukj,zkp(j),pkr(j),ptv,k)≤0∀(j,k)∈Ixlb≤xkj≤xub∀(j,k)∈Iulb≤ukj≤uub∀(j,k)∈Izlb≤zkj≤zub∀(j,k)∈Igterminal(xNj,zNj)≤0∀(j,N)∈I
目标由每个场景的一个术语组成,可以根据场景的概率进行加权 ω j , j = 1 , … , N s \omega_{j},\quad j=1,\ldots,N_{\text{s}} ωj,j=1,…,Ns 。每种情况的成本 J i J_{i} Ji 由下式给出:
J j = m ( x N + 1 j ) + ∑ k = 0 N l ( x k p ( j ) , u k j , z k p ( j ) , p k r ( j ) , p tv , k ) J_{j} = m(x_{N+1}^{j}) + \sum_{k=0}^{N} l(x_{k}^{p(j)},u_{k}^{j},z_{k}^{p(j)},p_{k}^{r(j)},p_{\text{tv},k}) Jj=m(xN+1j)+∑k=0Nl(xkp(j),ukj,zkp(j),pkr(j),ptv,k)
对于问题公式中直接考虑的所有场景,可行解保证约束满足。这意味着,如果所有不确定性只能采用离散值,并且这些值在场景树中表示出来,则可以保证约束满足。
对于线性系统,如果 p min ≤ p ≤ p max p_{\min} \leq p \leq p_{\max} pmin≤p≤pmax ,考虑场景树中不确定性的极值保证了约束满足,即使不确定性是连续和随时间变化的。这种非线性系统场景树的设计并不能保证所有约束都得到满足 p ∈ [ p min , p max ] p \in [p_{\text{min}},p_{\text{max}}] p∈[pmin,pmax] 。然而,对于非线性系统来说,最坏情况也往往处于不确定区间的边界 [ p min , p max ] [p_{\text{min}},p_{\max}] [pmin,pmax] 。实际上,仅考虑非线性系统的极值就可以得到良好的结果。
其他常用的稳健MPC方案(例如基于管的MPC)目前尚未在do-mpc中实现,但计划在不久的将来实现。请查看我们在Github上的开发路线图以了解详细信息和更新。
德国斯图加特大学–MPC
模型预测控制 (MPC),也称为移动时域控制或滚动时域控制,是最成功和最流行的先进控制方法之一。MPC 的基本思想是在有限的时间范围内预测受控系统的未来行为,并计算最佳控制输入,在确保满足给定系统约束的同时,最小化先验定义的成本函数。更准确地说,控制输入是通过在每个采样时刻求解有限时域开环最优控制问题来计算的;然后将所得最优输入轨迹的第一部分应用于系统,直到下一个采样时刻,此时时域会移动,整个过程再次重复。MPC 之所以特别成功,是因为它能够将硬状态和输入约束以及合适的性能标准明确地纳入控制器设计中。
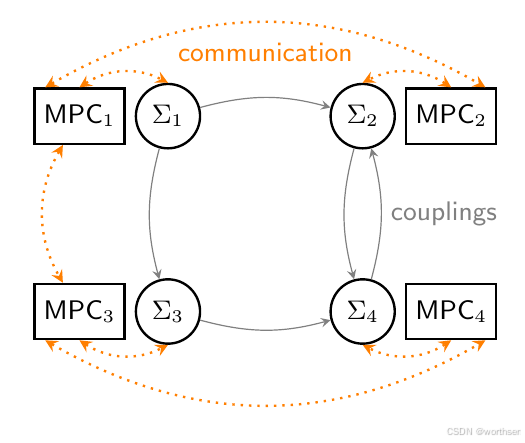
分布式 MPC
在大型动态系统和协作系统网络中,通常不可能或不希望用一个集中控制器来控制整个系统。因此,近年来,分布式 MPC 领域引起了广泛关注,其中每个子系统 ∑ i \sum_i ∑i 由 MPC 控制器本地控制,并与其相邻子系统交换有关预测轨迹的信息,以确保满足耦合约束并实现总体控制目标。在 IST,开发了分布式 MPC 方案,除了经典的设定点稳定目标外,它还适用于更一般的协作控制任务,例如包括共识和同步问题,或针对某些实际“经济”成本的最佳操作。
鲁棒 MPC
在鲁棒 MPC 中,目标是稳定不确定系统或受干扰影响的系统,同时确保约束的鲁棒满足。此类系统的行为无法准确预测。但是,如果知道不确定性的界限,则可以确定未来系统行为的界限。可以使用集合论方法确定可行性和稳定性。
许多现有的稳健 MPC 方案的缺点是计算负荷高,这是由于集值预测的复杂性以及这些方法引起的保守性。为了为非线性系统提供计算效率高的公式,我们使用基于增量系统属性的计算边界沿预测轨迹在线传播不确定性。然后,通过使用基于不确定性的预测边界的适当约束收紧来实现稳健性。我们展示了如何将这种方法扩展到具有移动障碍物的稳健避障情况。
我们还使用稳健的 MPC 方法结合机器学习的离线函数逼近方法设计快速、安全的近似显式 MPC。
在许多实际应用中,可用的计算能力可能会大大降低,因此无法采用在线稳健 MPC 方法。我们提出了一种离线方法,能够处理一般的不确定性,即状态和输入依赖性,该方法可以离线构建严格的约束集,因此相对于标称 MPC,计算负载保持不变。
稳健模型预测控制的集合论方法还可以扩展到主要目标不是稳定设定点而是根据能耗等经济标准以最佳方式运行系统的场景。我们提出了一种稳健的经济模型预测控制算法,该算法明确考虑了优化问题中可能出现的干扰,而不是优化标称行为,并且我们能够为平均和最坏情况性能提供界限,从而为经济目标提供稳健性。
随机MPC
在随机模型预测控制中,系统描述中的不确定性或外部干扰在设计过程中被明确考虑。与鲁棒模型预测控制不同,鲁棒模型预测控制通常假设不确定性未知但有界,并且所有可能的实现都应满足约束,而这种方法假设随机干扰或参数变化。此假设允许设计控制器来优化预期值或其他风险度量,而不是最坏情况。通过允许先验指定的约束违反概率,可以进一步提高性能。我们在随机模型预测控制中的研究重点是约束和目标的计算易处理公式以及确保递归可行性。为此,我们考虑了确定性和基于样本的方法。
通过 MPC 进行动态操作
研究最为深入的保证稳定性的 MPC 方法考虑了稳定给定稳态的问题,并使用离线设计的控制 Lyapunov 函数作为终端成本。然而,在实际应用中,控制目标往往更为普遍,涉及动态操作,例如设定点跟踪、轨迹跟踪、路径跟踪、输出调节或一般经济最优控制(例如,最小化能耗或最大化产量)。此外,最优操作模式(例如,最优周期轨道或稳态)通常会受到在线变化的影响,例如,由于外部设置的参考或价格信号的变化。最后,由于离线设计对于这种具有挑战性的设置而言非常棘手,因此在许多实际应用中,合适的终端成本的使用受到限制。
在 IST,我们旨在通过提供合适的分析和设计工具来弥合现有理论方法与实际挑战之间的差距。我们使用增量系统属性研究无终端成本的简单跟踪 MPC 方案的理论特性。此外,我们开发了参考通用离线计算,可用于获得适合非线性系统动态运行的终端成本。最后,我们通过将参考通用离线计算与人工参考轨迹/设定点相结合,设计了可以在在线变化的动态目标信号下可靠运行的 MPC 方案。
学习和自适应 MPC
稳健和随机 MPC 方法基于前向可达集的构建,这些前向可达集考虑了部分或全部不确定性的可能实现。尽管这些方法提供了理论保证,但由于对系统中的不确定性过度近似,它们往往过于保守。为了更好地估计系统,从而减少不确定性,可以采用系统识别中众所周知的技术。
自适应 MPC 将稳健和随机 MPC 的方法与学习技术相结合,以便在保证形式属性的同时通过不断更新的系统获得性能改进。值得注意的是,在这种情况下,MPC 控制器与所选的学习技术脱钩,因此它以所谓的确定性等价方式 (CE-MPC) 运行。
与自适应模型预测 (将系统学习作为控制动作的副作用) 不同,在学习模型预测 (也称为双自适应模型预测) 中,我们明确地在模型预测优化问题中加入了提高性能的方法。提供稳定性和约束满足等正式保证被视为一个开放点,也是我们研究的重点。
在文献中,学习 MPC 的主要方法可以细分为三类:
- 学习系统;
- 了解终端成本;
- 学习安全套装。
根据所选择的方法,性能和结果可能会有很大差异。
工业 4.0 MPC
工业 4.0 指的是未来几年工业生产中预计会发生的根本性变化。工业 4.0 一词并没有精确的定义,它包括各种使能技术和期望目标,需要在不同科学学科中进行研究。因此,IST 开展的工业 4.0 研究是跨学科的,将其在系统和控制理论方面的优势带入运筹学、工厂规划和管理的发展中。
在 IST,MPC 方法被研究是否适用于未来工厂的控制。虽然 MPC 在工业领域中的应用最为广泛,但很少考虑生产和装配系统。由于这些系统构成了不断变化的工业环境的很大一部分,因此开发了新颖的 MPC 方案,用于生产和装配系统的调度和动态重新调度。基于一种新颖的建模框架,该框架使这些系统可用于 MPC 方案的开发和系统理论分析,并给出了所需系统属性的闭环保证。
Review on model predictive control: an engineering perspective [2021]
Springer–Review on model predictive control: an engineering perspective
摘要
基于模型的预测控制(MPC)描述了一组先进的控制方法,这些方法利用过程模型来预测受控系统的未来行为。通过解决可能受约束的优化问题,MPC 隐式确定控制律。这将控制器设计的工作转移到对要控制的过程进行建模上。由于此类模型在许多工程领域都可用,因此 MPC 消除了应用控制的初始障碍。其隐含的公式保持了对系统参数的物理理解,从而促进了控制器的调整。基于模型的预测控制 (MPC) 甚至可以控制系统,这是传统反馈控制器无法控制的。在大部分理论都阐述完之后,是时候对其进行简要总结和应用驱动的调查了。这篇评论文章应该起到这样的作用。虽然在 MPC 成立之初,已经发表了几篇广受关注的综述论文,但今天却缺少对最新发展和应用的全面概述。本文回顾了当前的技术水平,包括理论、历史演变和实际考虑,以建立直观的理解。我们特别关注应用,以展示今天已经存在的可能性。此外,我们还详细讨论了一般植入细节和应对计算负担的策略——这仍然是 MPC 设计中的主要因素。除了 MPC 开发的关键方法外,这篇综述还指出了未来趋势,强调了为什么它们是 MPC 的下一个合乎逻辑的步骤。
介绍
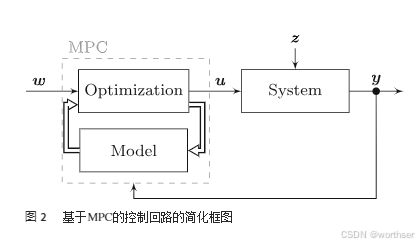
对于技术系统的自动化,反馈控制器(也称为闭环控制器)将参考 r 与测量变量 y 进行比较,根据产生的偏差 e = r−y 确定操纵变量 u 的合适值(图 1)。
根据工作原理,可分为:经典控制器、预测控制器和重复控制器。
经典控制器,如 PID 控制器、bang-bang 控制器、或状态控制器,只考虑过去和当前的系统行为(即它们对偏差是 “反应性的”)。
预测控制器使用系统模型来预测未来行为,预测与参考值的偏差。
重复控制器考虑前一个周期的系统行为,并计算下一个周期的最佳轨迹。
PID 控制器是最著名的控制器,在工业应用中具有突出的重要性和广泛应用。尽管存在几种设置规则,但通常很难找到参数化,特别是对于非线性或时变系统。
“任何反馈设计的有效性基本上都是”受系统动力学和模型准确性的限制。因此,即使在理论上,无论采用何种设计方法,仅靠反馈控制也无法完美跟踪时变参考轨迹。
特殊情况,例如执行器的技术限制,需要单独的解决方案,这些解决方案通常是基于启发式的,难以理解和维护。高级控制方法,如滑模控制器或后步控制器,在解释上同样抽象和复杂。
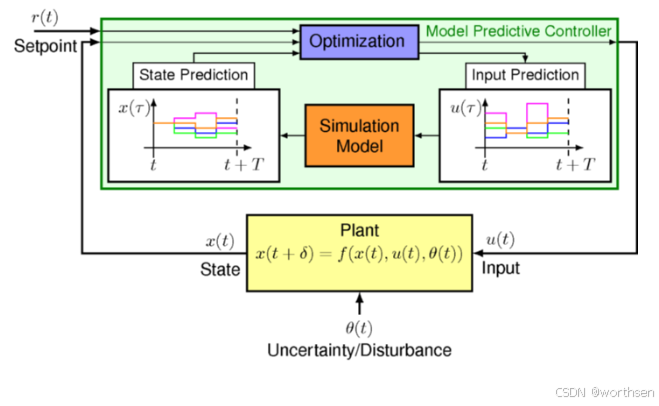
事实上,MPC理论的创始人强调,经典控制方法完美地适用于 90% 的控制问题。只有对剩下的一小部分问题才需要应用高级控制。相反,我们想要论证的是,MPC在几乎所有问题中都是一个合理的解决方案——甚至是在那些由于缺乏控制理论理解或对可行性缺乏信任而尚未得到控制的问题中。MPC基于对数学系统模型的重复实时优化。基于这个系统模型,MPC预测未来系统行为,并在优化中考虑它,以确定被控变量 u 的最优轨迹,如图2所示。因此,MPC通过调整过程模型提供了直观的参数化,但计算工作量比传统控制器要大。
其预测行为以及能够考虑硬约束的事实,使这种方法对控制系统非常有价值。随着计算能力的提高,以及复杂过程的模型对各种不同系统越来越可用,MPC 现在能够控制以前难以想象的系统。
MPC依赖于模型,这些模型在几乎所有学科中都有。这允许利用这种长期积累的知识,并节省了制定显式控制律的繁琐工作——这项任务通常是由控制专家保留的。相反,MPC通过基于模型的优化自动确定控制律。这种隐式公式、灵活性以及对模型的显式使用是MPC的主要优势,也是我们在工程界推广MPC的原因。本文将从应用的角度进行总结,但并不声称MPC是所有特定问题中所有控制算法的最优选择。
当 MPC 还是一个新概念时,关于其理论和应用的几篇广受关注的综述论文已经发表。相比之下,这篇综述是由这样一个想法驱动的:MPC不会永远是控制工程师的话题。今天,MPC理论的发展是由应用推动的,在这一过程中,制造技术刚刚开始发挥重要作用——通常对可靠性、约束和时间有挑战性的要求。这项工作应该激励非控制专家加入这一潮流,并开发新的用例,进一步推动技术限制的边界。
文章从基础理论开始,并简要概述了历史演变,以从最初的愿景和弯路中学习。重点放在可行性、稳定性和鲁棒性的实践考虑以及代表性应用上。在讨论过程中,我们讨论了MPC的不同变体,其中相关的关键词包括DMC、基于模型的预测控制、递减地平线控制等。
2 理论
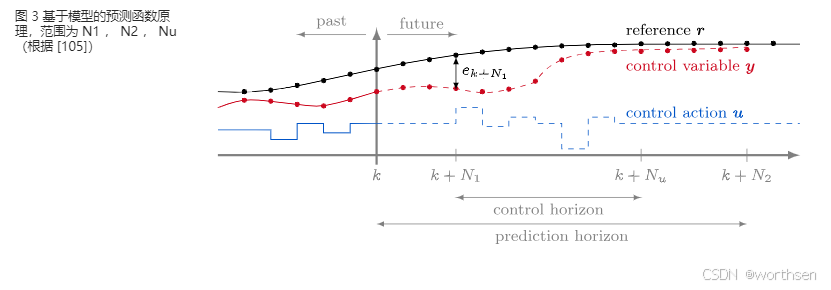
MPC 是一组高级控制方法,它明确使用模型来预测系统的未来行为。考虑到这个预测,MPC通过解决一个受约束的优化问题来确定最优输出 u。它是少数直接考虑约束的控制方法之一。通常,成本函数是这样制定的,使得系统输出 y 在 N2 的范围内跟踪给定的参考值 r,如图3所示。只有优化输出轨迹的第一个值被应用到系统中。这种预测和优化在每个时间点上重复进行。这就是为什么 MPC 也被称为“递减时域”控制。本质上,这个想法是通过短期(预测)优化来实现长期最优。由于认为近期预测的误差与远期预测相比是小的,所以假定这是真的。
预测与优化的结合是MPC与传统控制方法的主要区别,后者使用预先计算的控制律。
预测地平线 N2 必须足够长,以表示操纵变量u对控制变量y的影响。可以通过较低的预测时域N1或将它们纳入系统模型来考虑延迟。通常,将延迟纳入系统模型更为直观,较低的预测时域被设置为N1=1,以计算时间(因此,计算在一个时间步内完成,解决方案u在下一个时间步之前不会实施)。
假设一个任意系统。
x
(
k
+
1
)
=
f
(
x
(
k
)
,
u
(
k
)
)
x(k+1) = f(x(k), u(k))
x(k+1)=f(x(k),u(k)) ,(1)
y
(
k
)
=
h
(
x
(
k
)
)
y(k) = h(x(k))
y(k)=h(x(k)) ,(2)
MPC最小化用户定义的成本函数 J,公式(3),例如,参考向量 r 与模型输出 y 之间的跟踪误差,公式(4):
u
m
i
n
J
(
x
(
k
)
,
u
(
⋅
)
)
\overset{min}{u} \quad J(x(k), u(\cdot))
uminJ(x(k),u(⋅)) (3)
u m i n ∑ i = N 1 N 2 ∥ r ( k + i ∣ k ) − y ( k + i ∣ k ) ∥ \overset{min}{u} \quad \sum_{i=N_1}^{N_2} \| r(k+i|k) - y(k+i|k) \| umin∑i=N1N2∥r(k+i∣k)−y(k+i∣k)∥ (4)
u
l
b
≤
u
(
k
+
j
∣
k
)
≤
u
u
b
u_{l b} \leq u(k+j|k) \leq u_{u b}
ulb≤u(k+j∣k)≤uub
y
l
b
≤
y
(
k
+
i
∣
k
)
≤
y
u
b
y_{l b} \leq y(k+i|k) \leq y_{u b}
ylb≤y(k+i∣k)≤yub
对于所有的 i ∈ { N 1 , ⋯ , N 2 } i \in \{ N_1, \cdots, N_2 \} i∈{N1,⋯,N2} 和 j ∈ { 0 , ⋯ , N u } j \in \{ 0, \cdots, N_u \} j∈{0,⋯,Nu} 。
这种公式使用了任意范数 ∥ ⋅ ∥ \| \cdot \| ∥⋅∥。
我们将在时间点k预测的状态 k + i k+i k+i 称为 x ( k + i ∣ k ) x(k+i|k) x(k+i∣k) 。加粗的变量 A 表示更高维度,即向量(小写字符)或矩阵(大写字符)。一系列状态将由 x ( ⋅ ) x(\cdot) x(⋅) 表示:
x ( k + i ) ∀ i ∈ ( 0 , ⋯ , N 2 ) ⇒ x ( ⋅ ) x(k+i) \quad \forall i \in (0, \cdots, N_2) \Rightarrow x(\cdot) x(k+i)∀i∈(0,⋯,N2)⇒x(⋅),
u ( k + i ) ∀ i ∈ ( 0 , ⋯ , N u ) ⇒ u ( ⋅ ) u(k+i) \quad \forall i \in (0, \cdots, N_u) \Rightarrow u(\cdot) u(k+i)∀i∈(0,⋯,Nu)⇒u(⋅),
y ( k + i ) ∀ i ∈ ( N 1 , ⋯ , N 2 ) ⇒ y ( ⋅ ) y(k+i) \quad \forall i \in (N_1, \cdots, N_2) \Rightarrow y(\cdot) y(k+i)∀i∈(N1,⋯,N2)⇒y(⋅).
通过这种方式,约束公式将被缩写为
x l b ≤ x ( ⋅ ) ≤ x u b ⇒ x ∈ X f x_{l b} \leq x(\cdot) \leq x_{u b} \Rightarrow x \in X_f xlb≤x(⋅)≤xub⇒x∈Xf,
表示序列 x ( ⋅ ) x(\cdot) x(⋅) 在可行集 X f X_f Xf 中。
3 历史
在20世纪70年代末,[105]和[24]独立奠定了MPC理论的基础。随着数字控制器的出现,他们能够有效地控制复杂问题,展现出巨大的经济潜力。[105]在1978年引入了模型预测启发式控制(MPHC),它已经包含了MPC的所有特征:
- 一个明确的流程模型,由脉冲响应函数(IRFs)描述,
- 一个递减的时域,
- 输入和输出约束,
- 以及对控制(被操纵变量u的值)的迭代确定。
然而,[105]并没有声称获得最优控制。相反,未来的控制是迭代确定的,直到它们满足约束。“启发式”这个额外的术语强调了缺少明确的控制律。该技术是为具有多重输入多重输出(MIMO)系统、显著延迟和长处理时间的过程工业开发的[105]。他们甚至考虑在线识别流程模型——尽管仅用于设定点的变化。
大约在同一时间,来自壳牌石油公司的[24]开发了动态矩阵控制(DMC)。他们使用分段线性模型预测催化裂化装置的未来行为。因此,控制器意识到了工厂的延迟和其动态系统行为。Cutler和Ramaker使用了递减的预测地平线,并根据先前预测的输出与当前测量的输出之间的误差更新了模型系数。他们展示了DMC在性能上超过了经典的级联PID控制,并声称自1974年以来DMC已被应用于壳牌石油的控制问题。与MPHC的主要区别在于DMC计算最优控制变量。然而,控制问题的矩阵公式限制了DMC只能用于线性过程模型。
这两项工作为MPC在石油化工行业的广泛和快速传播奠定了基础。即使采用线性模型,采样时间也是数小时[97]。起初,重点是简化控制器设计并建立全面的理论,以便该方法可以在工业中使用[24, 34, 105]。MPC的潜力不仅基于预测,而且还基于它可以使用非线性模型——这两者都不受传统控制的支持。事实上,过程模型公式在MPC理论的初期是一个热门话题:脉冲响应公式(IRF)[105],分段线性步响应函数[24],ARMA模型[22, 23],或状态空间公式[56]。在选择模型公式方面的这种灵活性是MPC快速成功的关键原因之一。
最初的方法简单地忽略了模型不确定性和过程不稳定性——因为大多数化学工程过程是开环稳定的[35]。从20世纪80年代末开始,研究重点转向了MPC的鲁棒性和稳定性,这尤其是由MANFRED MORARI周围的研究小组特别追求的[13, 18, 19, 53, 144]。关于MPC稳定性和鲁棒性的详细讨论提供了第4节。
有有限地平线,即一个固定的移动窗口,(线性)估计问题可以被制定为一个二次规划问题[100],这在计算上是有利的。随着计算压力[14]引入了“显式MPC”,它将计算转移到大量的事先优化(第8.1节)。
随着千年的到来和计算机变得越来越强大,研究转向了应用。趋势是从大问题和长计算时间转向问题,这些问题具有较少的控制变量和对计算时间的更快要求。
4 可行性、稳定性和鲁棒性
人们必须区分 MPC 的几个方面:
- 开环优化问题的可行性,
- 闭环控制器的稳定性,以及
- 对不确定性的鲁棒性。
前者涉及优化问题的公式化,后者涉及控制器作为一个整体对干扰的处理,最后一个主要涉及过程模型的准确性。
在一个稳定的系统中,控制器设法在时域 N2 的末端将输出保持在恒定值,尽管控制回路受到干扰。相比之下,鲁棒性针对的是不确定性。它主要与模型在输出预测方面的不准确性有关。
模型是MPC的关键要素,但它永远不会完美[101]。然而,在稳定性分析中,假设模型是完美的。只有在后续步骤中才检查鲁棒性。此外,信号噪声是鲁棒性的一个重要话题[13]。Garcia和Morari[34]早就指出,最优控制改善了控制行为,但使鲁棒性检查复杂化。鲁棒性不是从稳定性中得出的,反之亦然[13],但闭环稳定系统总是减少了干扰的影响。
本工作在以下方面对MPC设计中那些分离的问题进行了明确的区分。
García等人[35]指出,对于每一个无约束的线性MPC,都存在一个等效的经典反馈控制器,它具有其经过充分验证的稳定性理论的所有好处。然而,不使用约束会失去MPC的许多魅力。因此,这更像是一种学术上的执着,而不是一个实际的选择。无限地平线MPC也是如此。对于线性MPC,有一个广泛的稳定性理论。对于状态空间形式的系统,稳定性分析基于特征值和单位圆盘,这与传统(线性)控制的稳定性分析中熟悉的一样[144]。然而,具有硬输入约束的优化问题通常是非线性的[101]。
确立稳定性——特别是鲁棒稳定性——对于非线性问题来说极其困难。这主要是因为缺乏控制算法的显式功能描述,这是大多数稳定性分析所需的[84]。如今,通过将成本函数制定为LYAPUNOV函数并引入终端集约束,实现了非线性、有约束、有限地平线MPC的稳定性[75, 77]。使用终端集将稳定性问题与约束满足问题联系起来[17]——讽刺的是,额外的约束稳定了一个有约束的非线性MPC。
鲁棒性是性能的权衡。几种方法以计算和最优性(例如L∞-范数)为代价提高鲁棒性。然而,只有在能够量化不确定性的程度时才能实现。为了保持MPC的关键特性——最优性——的一个实际折衷办法是,增加最坏情况预测必须收缩的要求[85, 144]。
5 MPC理论的最新发展
再次受到化工行业的启发,[58]将MPC集成到迭代学习控制(ILC)中,构建了一个专门用于批量处理的控制器。经典的迭代学习控制(ILC)在过程中作为开环控制工作,但会在周期或“迭代”之间调整命令配置文件。通过这种方式,它逐周期地接近理想配置文件,并可能对多个周期内的趋势做出反应。本质是“在先前运行中收集的信息可以用来改善当前运行的性能”[57]。与此相反,MPC是一个闭环控制器,但将重复任务视为彼此独立。
结合这两种方法构建了一个系统,它可以在一个周期或过程中对干扰做出反应(“随着它们发生”),并减少多个周期的跟踪误差。然而,将MPC集成到迭代学习控制(ILC)限制了其在固定时间操作中的使用,即时间样本的数量必须在周期中保持不变[58]。将这两种技术分开,让迭代学习控制(ILC)作为MPC的上层参考调节器工作,如[86]所进行的,可以克服这种限制。在这种组合中,MPC向迭代学习控制(ILC)引入了约束[57]。
Li等人[59]提出了这种组合的第三种变体,有效地成为一种最优迭代学习控制(ILC):他们取MPC的优化部分,即在地平线上优化被操纵变量,将其移植到迭代学习控制(ILC)中。得到的系统为每个周期确定了被操纵变量的最优配置文件。在随后的工作中,[60]建议平滑跨周期的命令。这基本上表明,最优解并不完全可信。这类系统只触及了MPC的一般性,因为它们缺乏递减地平线,并且有效地递归地过滤它们的最优控制。
在[66]和[128]的工作之间是迭代学习MPC与基于数据库的学习在控制理论中兴起领域的结合。前者利用k最近邻算法根据先前轨迹的整体目标和数据提取线性-二次调节器(LQR)的新轨迹。后者将迭代的、数据驱动的轨迹调整思想扩展到MPC的应用。
尽管也应用于重复任务,[78]专注于学习系统动态的模型而不是轨迹。作者利用数据和加权线性贝叶斯回归来模拟在重复路径上车辆动态的不确定性。同样,[50]应用高斯过程建模来详细说明可能轨迹的置信区间以保证安全。
数据驱动建模,如机器学习,可以用于MPC在其优化中使用的系统模型,或近似显式MPC的解空间,如[45, 71, 88],第8.1节所述。
学习的可能性特别是对于多智能体系统得到了增强,其中每个智能体都有助于数据采集和策略探索。[68]利用这种群体智能学习分布式MPC的轨迹。为此目的的学习问题被定义为在避免碰撞的约束条件下的二次优化问题。
6 应用
在约束存在的情况下的最优控制思想以及将控制律直观设计为优化问题,使MPC对许多不同任务都具有吸引力。最近,应用已经迅速扩展到所有工程领域。以下突出了主要的运动。
6.1 过程工业
长期以来,过程工业几乎专门使用MPC。这并不奇怪,因为石油化工行业决定性地推动了其发展[24, 97, 99, 105]。由于其复杂、多变量的过程具有时间延迟,MPC迅速传播,因为最优控制由于大的吞吐量带来了显著的经济效益。Darby等人[26]承认MPC是“今天在过程工业中实施有约束、多变量控制的标准方法”。
在MPC的创立论文中,[105]描述了三个应用案例:炼油厂催化裂化装置的蒸馏塔、蒸汽发生器和聚氯乙烯(PVC)工厂。催化裂化装置有两个被操纵变量(质量流量)和三个控制变量(温度),其中只有一个受到约束。该工厂通过十二个脉冲响应函数建模,采样时间为Ts = 3分钟——只有因为它使用了启发式控制律才可管理。通过控制聚氯乙烯(PVC)工厂,他们想展示MPC的多功能性,通过控制五个子过程。结果表明,受控变量的方差大幅减少,从而提高了质量和节能。令人印象深刻的演示为MPC的普及铺平了道路。
Richalet后来还描述了如何在MOBIL OIL的炼油厂控制一个蒸馏塔和一个真空装置[104]。目标函数已经制定为二次型LYAPUNOV函数,这有利于稳定性。他没有讨论鲁棒性,但提到了在故障情况下的备份控制系统。结果表明,控制器减少了质量标准的方差,回报时间不到一年。
石油公司是基于模型的先进控制器的推动者。Cutler和Ramaker[24]使用分段线性模型在SHELL OIL的一个催化裂化装置的炉子上进行控制。通过预测地平线N2 = 30和控制地平线Nu = 10,他们利用了预测潜力。
Prett和Gillette 97甚至使用了更长的地平线(N2 = 35, Nu = 15),采样时间为“几个小时”。他们连续线性化了一个非线性过程模型,以确定催化裂化反应器和再生器的最佳操作点。
由于蒸馏是化学过程工业中分子分离的主力军,它至今仍是MPC应用的热门示例,如[21, 80],这两项都是线性MPC的模拟研究。唯一的区别是[80]连续线性化了一个甲醇/水混合物的非线性模型,以应用线性MPC。
Piche等人[95]在MPC中引入了神经网络(NN)来控制聚乙烯(PE)反应器的设定点变化。神经网络(NN)是基于历史数据的非线性经验模型。这种机器学习模型目前正在受到特别的关注。从传统的(开环)工厂测试中构建线性动态模型,以在其设定点控制工厂。Piche等人实现了30%更快的过渡和受控变量变化的整体减少。这个想法仍在积极研究中。Li等人[63]也在MPC中探索了神经网络(NN)的连续线性化,但用于控制搅拌反应器的温度——这是过程工业中的一个常见应用,例如生物反应器。Shin等人[117]使用神经网络(NN)(全连接,14-15-2)与MPC用于丙烷脱气器(例如专门的蒸馏塔)。尽管声称基于神经网络(NN)的非线性MPC比线性MPC表现更好,但他们在传统的PI控制上对新控制器进行了基准测试,展示了更快的60%的稳定时间(使用神经网络(NN)-MPC为35分钟,使用PI控制为92分钟)。他们进一步强调了使用NN结合MPC的额外好处,即数据驱动模型的更容易建模。Nunez等人[89]使用了一个更复杂的神经网络(NN)结构,一个循环神经网络(RNN)(实际上是一个基于注意力的编码器解码器循环神经网络(RNN),有23,000个自由参数),用于模拟一个工业过去的增厚过程。采样时间为Ts = 5分钟,给控制器足够的时间进行全局优化与粒子群优化(PSO)——一个相当不寻常的选择——对于预测和控制地平线N2 = 10和Nu = 5。作为实际工业部署的一个罕见例子,他们展示了控制对工业工厂一天工作的有效性。基于循环神经网络(RNN)的MPC能够维持浆料增稠器的目标浓度,尽管泵出现严重故障。循环神经网络(RNN)结构也用于控制链式搅拌反应器[136]。还有具有不同特点的其他网络类型的应用,例如回声状态网络用于模拟缓冲罐的时间延迟,例如用于冰箱压缩机试验台的(非线性)MPC[9]。
总的来说,除了石油和天然气以及化工行业,制药和生物工业还使用MPC来管理其过程的非线性与大时间延迟的耦合,例如在发酵过程中[42]。Ławrynczuk[6]再次将线性MPC与非线性MPC进行了比较,用于搅拌反应器和蒸馏塔。他得出的结论是,特别是对于蒸馏过程,非线性控制器更具经济性。在此基础上,他建议将两种方法结合起来,减少纯非线性MPC的计算负担:仅在第一时间k = 1应用非线性优化,并在其他步骤1 < k < N2中使用线性化模型。据作者所知,这种方法尚未得到进一步的检验。
Prasad等人[96]选择了不同的路线,更倾向于使用多个线性模型而不是单一的非线性模型。他们控制了一个圆锥形罐的填充高度。由于直径随着高度的连续变化,他们建议在不同高度识别三个单独的线性模型,为每个设计一个控制器,并将输出组合成一个集合,以获得操纵变量(入口流量)的一般输出。
在2003年,[99]已经统计了超过4600个工业应用,回顾了MPC的可用商业软件包。它们在模型结构、其识别以及约束是如何实现的(作为硬约束或作为成本函数中的额外惩罚项)方面有所不同。尽管如此,所有模型都是线性的、时不变的,并且由经验测试数据导出。在线模型适应不受任何软件的支持,尽管从一开始就已经有了(学术)关于这个问题的工作,例如[105]。
尽管稳定性理论已达到成熟水平,但作为商业MPC软件的主要供应商,ASPENTECH假设无限时域控制以确保稳定性,这在实践中通过预测地平线比系统的反应时间大得多来实现[33]。就学术界而言,来自MATHWORKS的软件MATLAB/Simulink非常流行,例如[80, 96, 108]。
今天,过程工业仍然是MPC的主要用户[76],发展到更快的机械过程,如造纸机[145]或磨石机[108, 124]。再次,由ANGLO AMERICAN PLATIUM公司展示了一个工业应用报告,其中线性MPC(更准确地说:DMC)超越了当时著名的模糊控制器[124]。使用ASPENTECH的商业系统,大型磨石机的功耗降低了66%。然而,并没有完全信任这种新的控制方法,已建立的模糊控制器被作为异常状态的备份选项运行。
Olivier和Craig[92]以及同事们[55]在过程中检测执行器的故障,以更新MPC可用的被操纵变量,保持控制性能。他们使用粒子滤波器来估计某个执行器是否仍然可以使用(二元决策)。自我意识对于在恶劣环境中持续运行的大型系统尤为重要。他们模拟了一个矿业设施的磨矿机。模拟表明,如果MPC知道执行器故障,它可以管理执行器故障。
表1总结了讨论过程中工业的关键参数。只有那些提供了MPC实施细节的工作才被列出。顺序除了发布顺序外没有意义。
MPC通常作为经典PID控制器的监督控制,形成一个级联控制回路。大型多输入多输出(MIMO)系统、经验模型——大多数是通过步骤或脉冲测试导出的[99]——和长时间的计算时间Ts > 1h支持了过程工业中的MPC。今天,采样时间已经大幅减少到分钟和秒的区域[26],表1。过程变量之间的复杂耦合需要经验的非线性模型,这些模型通常最初是线性化的。
6.2 电力电子
直到21世纪中期,电力电子领域才形成了相反的趋势。这些极快的单输入单输出(SISO)系统使用纯分析模型在亚毫秒级的采样频率下工作[15, 52, 65, 129]。这些特征与过程工业截然不同。Richalet [104]很早就预见到了这种反向运动,报告了一个采样时间为Ts < 1ms的伺服驱动控制应用。为了实现如此短的采样时间,通常使用相对简单的模型、短的地平线,并且经常使用优化问题的显式解。显式MPC通过提前为各种情况解决优化问题来获得显式(线性)控制律的多面体[14]。这增加了整体计算工作量,但将其转移到了离线优化上。
Linder和Kennel [65]使用显式MPC应用MPC进行电气交流驱动的“场向控制”。结果令人清醒:对于大信号步长,与常规PID控制器相比几乎没有改进。对于小步骤,MPC更快更好地达到了新的目標值,但总的来说,Linder和Kennel认为MPC的潜力更多是由于直观调整和满足约束等特性。
尽管如此,Bolognani等人[15]认为MPC非常适合电动机控制,因为存在准确描述电动机行为的分析线性模型。他们也使用显式MPC公式实现了一个采样时间Ts = 83ms。由于预测地平线N2 = 5远未覆盖完整的驱动动力学,无限预测地平线的假设不成立,使得稳定性成为一个主要的(未考虑的)问题。如果负载扭矩与MPC设计的设计扭矩相匹配,则控制是完美的。否则,就会出现期望值和实际值(电流、电压等)之间的偏差。尽管如此,控制器工作稳定,并可靠地强制执行电流和电压限制。
Kouro等人[52]就功率转换器控制方面检验了MPC。功率转换器只有有限数量的离散状态n。这妨碍了需要启发式方法(混合整数优化)的优化。他们采取了一种暴力方法,测试了所有可能的控制动作,导致计算量呈指数增长:nN2。对于n = 7个转换器状态,为了实现采样时间Ts = 100ms,预测地平线限制为N2 = 2。与经典PID控制相比,他们得出的结论是MPC的优势在于其在控制变量和约束方面的灵活性——与之前的[65]类似。
Geyer等人[38]使用MPC进行电动机的直接转矩控制。控制问题包括保持电动机扭矩、定子磁通的大小和变流器的中性点电位在它们的(滞后)范围内,同时最小化变流器的开关频率。
为了降低计算复杂性并在Ts = 25ms内解决MPC,控制和预测地平线被限制在Nu = N2 = 2。作为计算工作量和系统行为之间的折衷,预测地平线的值被线性外推100步,以大致识别未来的系统行为。仿真结果表明,MPC在遵守约束方面只有轻微的改善,但平均减少了25%的开关频率,从而降低了功耗。
作为对此的实验验证,Papafotiou等人[93]在1.5MW电动机驱动上实现了MPC的直接转矩控制。再次,主要关注点是计算速度,因此控制地平线进一步减少到单步Nu = 1。两个控制任务,电动机磁通和电动机速度,被分成具有不同执行时间的单独控制任务(分别为25ms和100ms)。结果无法维持上述仿真的兴奋。平均而言,控制将变流器的开关频率降低了16.5%,同时保持了与标准控制相同的输出质量。对于这种规模的电动机驱动,实现的更快的转矩响应对某些应用更有价值。特别是高压应用,如电动机控制,必须考虑变流器的时间延迟[10]。变流器通常在开关后显示编程时间延迟,以避免直通。基于模型的预测控制(MPC)可以简单地管理这一点,例如在系统模型中[10]。
电力电子领域的应用数量增长如此之快,以至于Vazquez等人[129]感到有必要对学术实现进行广泛的回顾。他们得出的结论是,适当的模型的缺乏仍然是通往工业应用的主要障碍。而MPC在功率转换器和整流器(将交流(AC)转换为直流(DC)的电气设备)方面的应用仍然是积极研究的主题,这是由于它们的普遍性。由于社会在抗击气候变化和随之而来的整个工业电气化背景下的转型,这种应用可能会进一步增加。效率是首要的,研究人员发现MPC在确定转换器和整流器的最佳开关序列方面提供了宝贵的贡献,例如对于中压等级[40, 83]。尽管计算仍然是一个问题,例如[2],但在这个电力电子领域的非常快速控制问题的领域中,两种公式仍在竞争:在线解决控制问题的MPC的标准隐式公式和事先为所有情况解决优化问题的显式公式。关于显式MPC的详细一般讨论包括第8.1节。
再次,表2提供了MPC在电力电子应用中的工作概要。它强调了在这个领域中使用的MPC参数的多样性。从控制单个电子元件开始,特别是转换器,电气工程的应用已经扩大到控制多个组件的系统,正如下一节将展示的。
6.3 建筑气候与能源
自2010年以来,MPC已经引起了建筑气候控制界的注意。在具有长预测地平线的非线性多输入多输出(MIMO)系统中,分析模型和经验模型相结合。典型的采样时间以分钟到1小时计,预测时间通常小于48小时[113]。目标始终是在保持一定(热)舒适度的同时减少能源消耗。MPC在这一领域的成功归功于它允许纳入统计不确定性甚至天气预报[5],例如在[90]中。
用于供暖、通风和空调(HVAC)的MPC已经应用于从单个房间到大型空间,如机场建筑或多房间问题,如办公楼[1]。绝大多数工作涉及非住宅建筑,只有4%包括住宅建筑,通常作为微电网中的其他能源汇之一[74]。在他们最新的回顾中,他们指出供暖、通风和空调(HVAC)在建筑能源管理系统领域发挥着重要作用,超过50%的出版物;MPC是最常用的策略。作者将其归因于其对天气和占用预测(例如需求预测)的天然考虑。谷歌报告称,MPC提高了他们数据中心的空气处理效率,从而将冷却成本降低了9%[54]。
在气候和能源管理领域,大多数工作都是模拟,因为实施工作量大,存在不适风险。Gunay等人[43]实际上在他们大学办公室的一个实际房间展示了他们的发现;Ma等人[69]在他们大学建筑的冷却系统上实施了一个MPC控制器。主要组件是一个冷水储罐,其操作被控制(何时填充,填充速度,输入水应多冷——来自冷水机等)。他们通过引入优化财务成本而非纯粹能耗的有趣想法,将能源成本降低了19%,[1]后来在该领域再次拾起。如今,“MPC”已成为这类公式的专门术语。
Yu等人[141]在热室中的一个小模拟建筑上对不同的温度控制方法进行了整体基准测试。基于模型的预测控制(MPC)优于其他方法——包括具有可编程时间表的商业恒温器——并将能耗比恒定温度控制器降低了43%。然而,结果表明,对于小型建筑,主要好处来自于增强的温度测量。
建筑气候控制中的工业应用MPC仍然很少,这是由于巨大的建模工作量(高达控制工作的70%)[5, 94]。通常,单独的房间被建模为容量电阻元件[82, 90, 91, 107]。基于物理原理的耦合电阻-电容模型和纯粹的经验方法是用于MPC的建筑能源系统的两种主要建模类型[113]。
解决建模工作量和相关领域知识要求的一种方法是使用黑盒建模方法,即来自机器学习领域的。Qin和Badgwell[99]已经注意到,神经网络(NN)很受欢迎,用于为MPC建模未知的非线性行为。Afram等人[1]使用NN对能源管理系统的各个子系统进行建模,如通风、热储存或热泵。模型准确性的提高是以MPC中的非线性优化为代价的。系统在历史天气数据上进行了测试——假设在每个点都有理想的天气预报,这是常见的做法,例如也在[36, 90, 91]中。不幸的是,[1]中没有给出MPC参数的详细信息。目标是优化能源消耗的成本,而不是消耗量本身。为此,提出的基于神经网络(NN)的MPC将能源消耗转移到电力价格的非高峰时段,使用建筑的质量作为储存。这对于温和的天气条件效果极佳,但在极端条件下失败,如仲夏时节,这种被动热储存是不够的。
建筑气候控制中相互交织的个体模型导致了复杂的优化问题,基于梯度的算法可能失败,更可取的是基于启发式的全局优化[82]。这进一步增加了计算工作量,因此扩大了采样时间,但由于热行为的惯性特性,这很少是问题。如果房间数量变大,控制问题被分解为多个解耦的MPCs,以较低的计算成本实现近乎最优的解决方案[82]。Shaltout等人[5]呼吁建立一个分布式的MPC控制器网络,相互合作。
Gunay等人[43]声称,较短的采样时间有利于温度控制(Ts,short = 10分钟与Ts,long = 1小时,均为N2 = 6),因为模型准确性通常随着预测时间的延长而降低。此外,长地平线可能被随机干扰破坏,如占用行为。他们声称,短预测地平线TN2 = 6小时甚至可能消除了对准确天气预报的需求,并使MPC更加反应灵敏。Yu等人[141]支持了短地平线使给定温度参考的更准确跟踪的发现。相反,[91]认为应使用TN2 = 24小时作为供暖、通风和空调(HVAC)系统的预测地平线。
Park和Nagy[94]通过挖掘出版物的关键词,确定MPC是供暖、通风和空调(HVAC)控制的最新趋势,并预测它将向智能电网控制领域扩展。另一篇关于供暖、通风和空调(HVAC)系统的MPC的最新回顾[113]强调,随着向可再生能源和其更高变异性转型的电力发电,它的重要性将随之增加。事实上,将灵活的源和汇集成到电网(由可再生能源工厂和PEVs引入)的压力不断增加,需要先进的控制方法,例如[126]。
特别是,能够包括随机模型,从而明确地对不确定性进行建模,被认为是能源管理领域的一个独特特征[11]。Oldewurtel等人[91]将MPC问题制定为概率问题,考虑天气预报的不确定性。Morrison等人[86]没有使用天气预报,而是学习了由于季节趋势导致的太阳能日变化。算法学习了人类在热水需求方面的日周行为,而MPC在较低层(TN2 = 12小时)上实现了这个学习参考。在模拟研究中,他们为所考虑的热储存罐系统模拟了从仲夏到仲冬的四周。同样,在可再生能源领域,Dickler等人[27]应用了时变MPC来减轻风力涡轮机的负载和功率平衡,其中机械需求模型在每个控制步骤中针对当前预测和控制地平线进行了线性化。风速作为机械结构上的主要负载之一,通过纳入风速预测来处理。Sun等人[125]使用MPC来平滑风速波动对风力涡轮发电机产生频率的影响。这个想法是在线性化MPC中同时考虑涡轮机和风本身的动态。Shaltout等人[114]采纳了同样的想法,将风力涡轮机与储能系统耦合。针对多个目标,其中一些具有非技术动机,他们制定了所谓的经济MPC。将波动的能源消费者添加到这样的系统中,[126]模拟了一个(连接的)微电网,有一个风力发电供应商和100辆PEVs。目标是最小化整体运营成本:最大化风能消耗,最小化与主电网的交换,即在消费和生产高峰之间平衡能源消耗。PEVs可以用作源或汇,只要它们在工作日结束时完全充电。PEVs的能源需求被建模为截断的高斯模型;风力涡轮机的供应在自回归积分滑动平均模型(ARIMA)中。他们提出了一个双层MPC,顶层平衡整体电力需求,将PEVs聚合为一个单一值,而底层MPC处理将能源分配给各个PEVs。顶层优化了能源成本和风险,这是通过蒙特卡洛模拟和随机模型确定的。模拟表明,与立即充满电策略相比,成本可以降低30%以上,在这种策略中,电池一连接到电网就充满电。这可能加剧微电网在高峰时段的能源不平衡。Schmitt等人[109]通过建立双层MPC来优化混合动力汽车的能源管理。在更高级别的非线性MPC中,包括基于规则的齿轮选择在内的驾驶策略被优化,物理系统的控制和驱动在更快的底层线性MPC中实现。
在交通电气化的到来之际,MPC正在经历新的繁荣,例如在平衡混合动力汽车的燃油消耗时也考虑了个人驾驶行为[61],或在健康意识电池充电[147]中。
再次,能源转型和能源效率的超级趋势将导致对智能能源平衡策略的需求不断增加,特别是在(微)电网和建筑能源管理系统中。这反过来将需要更多的先进控制策略的应用,特别是MPC[74, 113]。该领域已经从控制纯供暖、通风和空调(HVAC)系统发展到整个消费-生产系统(或网络)。模型的复杂性代表了这种演变,表3。
6.4 制造业
制造业是MPC相对较新的应用领域,可以被视为新发展的代表:MPC不再替代现有的控制器,而是利用新的控制任务。我们想特别强调一般制造业领域,尤其是切削技术领域,一些论文已经展示了高级控制的潜在好处,例如在概念基础上[28]。
尽管如此,首先,为了实现更高的精度,对机床中心的位置控制回路进行了固定增益控制器的替代[122, 123]。用MPC补偿高精度铣削中的动态仍然是一个活跃的研究领域,例如[73]。尽管如此,应用发展到了引入MPC的额外高级控制。控制转向了过程控制,而不仅仅是实现机床设置,创造了前所未见的好处。Mehta和Mears[79]描述了一个控制车削中细长杆偏转的概念。Zhang等人[142]检验了MPC以避免铣削中的一种不受欢迎的共振现象——颤振。MPC使用了一个线性化振荡模型,假设质量、阻尼和刚度是已知的。控制器操纵刀具夹头的一个外部力执行器。在模拟中,系统将无颤振区域扩大了60%。
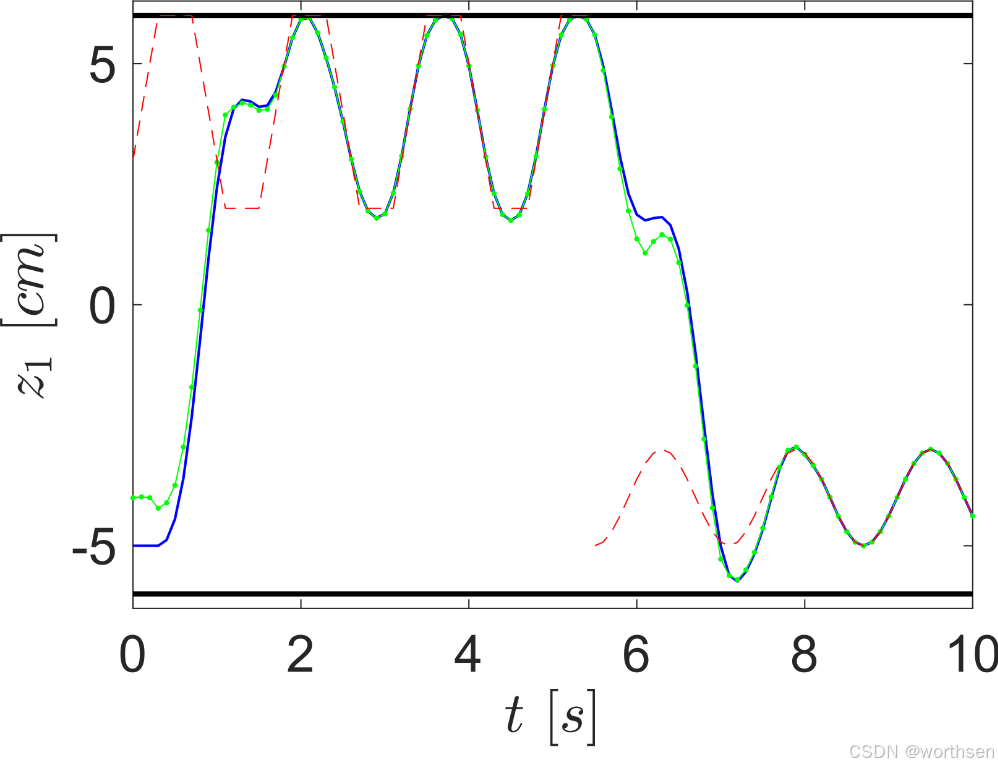
首个约束MPC用于铣削中的力控制是在德国亚琛工业大学实施的[111, 112, 119, 120]。他们通过操纵进给速度来实现这一高度动态过程中的恒定力。后来,增加了一个黑盒模型(支持向量回归(SVR))来考虑机床的非线性[7, 8]。
在金属加工领域,Liu和Zhang[67]引入了基于MPC的控制到焊接中。预测N2 = Nu = 5下一步(Ts = 0.5s),他们控制焊缝的穿透深度作为质量的度量。虽然第一种方法依赖于专用视觉系统和穿透深度的线性化模型,但一种更新的方法放弃了视觉系统:[148]。通过在线识别一个描述与穿透深度关系的模型来关闭反馈循环。这与上述铣削过程的设置类似。这些方法展示了对系统变量的控制,这些变量在没有MPC的情况下很难或不可能控制。
Wehr等人[133]应用线性MPC控制精密冷轧薄窄带的间隙。给定过程的结构因存在两个冗余的间隙控制执行器而在解剖学上过度驱动。通过引入单一的时变优化变量来同时解决过度驱动和MPC的计算工作量,该变量利用了过程中执行器的不同可用性。
Wu等人[135]解决了生产技术的不同领域,他们优化了织布中插入纬纱的气喷。这是减少织布机(以压缩空气形式)能耗的关键。对于塑料注射成型,Reiter等人[103](概念性)和后来的Stemmler等人[121]构建了一个控制模具内压力的MPC。这个想法是获得恒定的产品重量作为质量标准。通常使用不同的控制器分别控制不同阶段(注射和包装阶段),而MPC能够同时处理两个阶段并优化过渡(这原本是控制器的切换)[121]。提高MPC的可用性是这项工作的主要驱动力。
更一般地说,"生产"领域增加了自动化和搬运系统的范围。这些通常是基于图或状态建模的,例如Cataldo等人[20]对托盘运输和加工系统使用Petri网进行了建模。使用MPC,他们使系统能够适应运输线上的故障,如堵塞部分。具有离散状态的自动化应用提出了混合整数优化问题。它们需要专用求解器,这些求解器通常基于启发式,并且比基于梯度的优化器具有更大的计算负担。
表4提供了所选参数的快速概览。与早期的电力电子作品相比,采样时间相当低,预测地平线相当大。
6.5 更多应用
除了这些主要应用之外,工程领域的应用范围是巨大的。从平衡行走机器人[134]、悬挂起重机负载[110],到重型卡车的巡航控制[62, 140],再到优化视频流的缓冲和质量[138]。即使在水下机器人的路径跟踪中,也应用了MPC[116]。在几乎所有应用中,MPC的性能都优于传统控制器。
特别是,机器人技术是MPC应用的新兴领域,例如[47, 88, 134]。虽然仿人机器人是一个特殊案例[134],但工业机器人如今在车间里无处不在。轻量级、经济型和协作机器人的成功促进了这一领域与MPC相关的工作的显著增加。Nubert等人[88]通过鲁棒MPC普遍提高了跟踪鲁棒性。而[47]则利用轻量级机器人的力反馈来打磨金属工件的自由曲面。MPC在移动过程中保持对变化区域的给定压力。
随着车辆动力概念的新兴,控制策略的新应用和MPC的应用也随之而来。无论是轮毂电机的牵引控制[?],巡航控制[61, 62],还是自动驾驶的路径规划[48]。先进的巡航控制重点仍然是大型商用车辆,如(混合)电动公交车[61, 137],因为它们可以更快地获得投资回报。看来,动力传动系统的电气化将电气工程知识传播到了车辆的开发周期中,并随之带来了控制工程专业知识。
6.6 注释
尽管许多研究人员在描述他们使用的模型时表现出非凡的一丝不苟,但有些人忽略了提供有关MPC调整的基本信息。我们想强调,至少应该列出采样时间Ts和所有地平线(下预测地平线N1、上预测地平线N2和控制地平线Nu),正如表1至表4所示。
理想情况下,还应该提供成本函数,包括松弛变量ξ的权重。有了给定的地平线,就可以比较应用,估计计算工作量。确切的成本函数是重现结果的需要,确保良好的科学实践。
9 结论
MPC之所以流行,“很大程度上是因为,给定合适的模型后,控制器可以容易地实现,并且可以直接理解要调整的参数,以及容易处理约束”[104]。随着微处理器的巨大进步和模型的无处不在,这一点比以往任何时候都更加正确。MPC的一个关键特点是通过在线解决受约束的优化问题隐式确定控制律。在优化问题中纳入物理约束将设计控制器的工作转移到要控制的系统建模上[35, 104, 105]。
要使MPC对工业产生持久影响,需要克服的障碍是建模的复杂性和算法调整。在大多数情况下,潜在的好处不值得付出建立建模、优化和控制理论专家知识的劳动。
建模通常是最耗时的活动[44]。随着微处理器时代消除了计算资源作为最大障碍,为MPC的持久成功铺平了道路,第二个时代可能由使用数据驱动建模降低障碍的使用来预示。机器学习使得复杂系统的轻松描述降低了将MPC应用于新过程的障碍。对于应用,首先已经覆盖了极端情况:具有长采样时间的大型和复杂的多输入多输出(MIMO)系统(石油化工行业)。然后,几乎作为一种反向运动,开发了具有短采样时间和通常有显式公式的快速系统(功率转换器)。如今,狂热已经平息,让这个领域有了合理的采样时间。尽管计算能力有了巨大的提高,即使在今天,高效的计算应该是座右铭,但需要专家级的编程知识,阻碍了即插即用的使用。Forbes等人[32]得出结论,工业需要的是提高现有技术的可用性,而不是新的MPC算法。如今,几乎可以说重点已经从理论转移到了应用,让两者共同进步。理论再次成为应用驱动的——就像它在最初的时候一样。
我们相信,全球化的脱碳趋势将进一步推动MPC在电子领域的应用,由于电气化的扩大以及对电力元件高效率的不断迫切需求。基于模型的预测控制(MPC)可以在许多领域提高效率,例如在气候控制系统中(精确供暖、通风和空调(HVAC))。它们处理反应迟缓的系统和相当精确的预测模型,例如房间占用或天气,这使MPC非常适合它们。
新趋势的萌芽和成熟学科的粗壮树干表明,在我们看来,MPC应用数量指数增长的一步之遥。
基于模型的预测控制(MPC)能够控制高级目标,而不仅仅是机床设置点。本综述应鼓励领域专家将这种智能控制方法应用于他们的领域,播种下一代制造业。
参考
1、wiki–Model predictive control
2、MathWorks–what-is-mpc
3、do-mpcBasics of model predictive control
4、德国斯图加特大学–MPC
5、stanford–MPC
6、sc.edu – Model Predictive Control
7、Springer–Review on model predictive control: an engineering perspective
8、ControlSystemsSynthesis–MPC