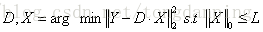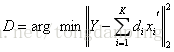稀疏表示（二）——KSVD算法详解（结合代码和算法思路）

tongdanping 2018-01-26 19:36:39

25730

分类专栏：稀疏表示

            </div>
            </div>
                            <div class="up-time"><span>最后发布：2018-01-26 19:36:39</span><span>首次发布：2018-01-26 19:36:39</span></div>
            <div class="slide-content-box">
            <div class="all-tags-box">
                                </div>
                                                                <div class="article-copyright">
                        <div class="creativecommons">
                            <a rel="license" href="http://creativecommons.org/licenses/by-sa/4.0/"></a>
                        </div>
                        <div class="creativecommons">
                            版权声明：本文为博主原创文章，遵循<a href="http://creativecommons.org/licenses/by-sa/4.0/" target="_blank" rel="noopener"> CC 4.0 BY-SA </a>版权协议，转载请附上原文出处链接和本声明。                            </div>
                        <div class="article-source-link">
                            本文链接：<a href="https://blog.csdn.net/tongdanping/article/details/79170375">https://blog.csdn.net/tongdanping/article/details/79170375</a>
                        </div>
                    </div>
                                                                            </div>
            <div class="operating">
                                                            <a class="href-article-edit slide-toggle">版权</a>
                                </div>
        </div>
    </div>
</div>
<!--python安装手册结束-->
                <article class="baidu_pl">
             <div id="article_content" class="article_content clearfix">
        <link rel="stylesheet" href="https://csdnimg.cn/release/phoenix/template/css/ck_htmledit_views-3d4dc5c1de.css">
                        <div class="htmledit_views" id="content_views">
                                        <p>鉴于很多人要代码，我放到网盘里吧：</p>

链接: https://pan.baidu.com/s/1sVMl3s-c7U1aaI9jzr3DTw 提取码: 55wx

——————————————————————我是分割线————————————————————————————

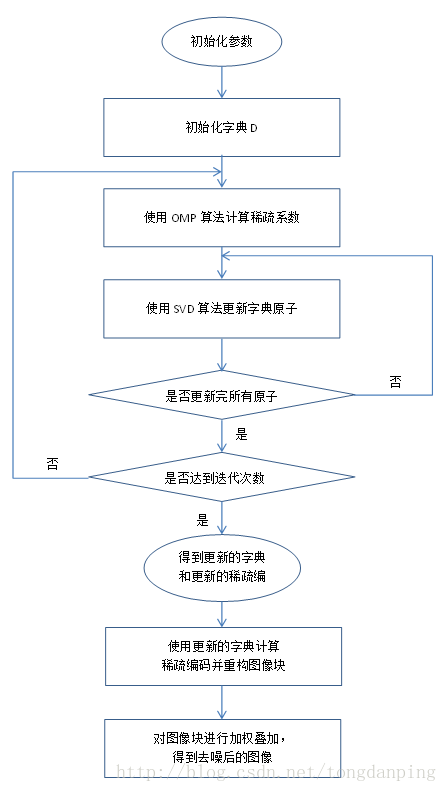
KSVD是一种稀疏表示中字典学习的算法，其名字的由来是该算法要经过K此迭代，且每一次迭代都要使用SVD分解。

在KSVD去噪算法中，稀疏编码可以使用OMP或者任意其它的稀疏编码算法，KSVD是用于字典更新的算法，KSVD在字典更新的过程中，每次只更新一个原子和对应的稀疏编码向量，在更新该原子时，其它原子是不变的，每次更新完字典的所有原子就同时更新了系数编码系数，这叫作一次迭代，在KSVD算法中，可以选择稀疏表示的第2种模型或者第3种模型见我的上一篇文章，在程序中可以通过参数 errorFlag来设置，如果errorFlag 为0，表示是用第2种模型，如果errorFlag 为1，表示是用第3种模型。在程序中的参数说明如下：

%    errorFlag...              if =0, a fix number of coefficients is
%                                 used for representation of each signal. If so, param.L must be
%                                 specified as the number of representing atom. if =1, arbitrary number
%                                 of atoms represent each signal, until a specific representation error
%                                 is reached. If so, param.errorGoal must be specified as the allowed
%                                 error.

在这里，我们使用第2种模式，也就是令errorFlag 为0。

整个KSVD的算法流程如下：

字典的初始化可以选取原始数据中的K个原子，或者使用一个固定的字典，比如DCT字典。

稀疏表示的两个主要阶段如下：

第一阶段：稀疏编码

对于模型：

此时的字典是已知的，利用OMP算法，计算得到稀疏编码矩阵X，在得到X后，进入第二阶段。

第二阶段：字典学习

在第一阶段中已经计算好了X，因此模型可以简化为：

在这里把矩阵用向量表示：

那么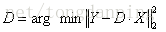，可以被简化为：

即把一个秩为K的矩阵分解为K个秩为1 的矩阵相加，现在假设我们要跟新第k列的原子，那么其他原子固定，即

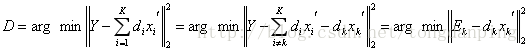
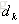
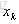
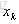
这里看出，当更新第k个原子的时候，只考虑第k个原子和稀疏向量带来的表示误差，这里问题就转化为求解一个最接近的秩为1的矩阵，得到该矩阵以后，通过SVD分解，就可以得到更新后的和（这里请看文章末尾的TIP1对SVD分解的简单介绍）。但是这样更新以后的非零的位置和更新前不再一样，甚至可能不再是稀疏的，这就违背了稀疏表示的初衷，因此在这里，应该做一点处理：

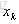
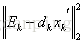
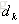
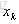
在这里，我们只保留上一次迭代中使用到了第k个原子的计算的最小误差来更新和。

接下来，我们将结合KSVD去噪的程序来说明KSVD算法的流程。KSVD去噪算法可以在pudn上下载，去噪的程序denoiseImageKSVD.m 和 KSVD算法的程序 KSVD.m 都在文章末尾。接下来我们将把程序的每个部分提出来分析其功能。

KSVD的核心程序如下：

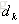
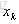
在程序中使用了I_findDistanseBetweenDictionaries()函数来更新和。

rPerm = randperm(size(Dictionary,2));%size(Dictionary,2)=256 ，该函数产生1到256的随机的整数
for j = rPerm  %j的值为从1到256的随机整数值（没有重复的）
    [betterDictionaryElement,CoefMatrix,addedNewVector] = I_findBetterDictionaryElement(Data,...
            [FixedDictionaryElement,Dictionary],j+size(FixedDictionaryElement,2),...
            CoefMatrix,param.L);
    Dictionary(:,j) = betterDictionaryElement;
    replacedVectorCounter = replacedVectorCounter+addedNewVector;
end

这个函数是随机的更新字典中的每个向量，其中I_findDistanseBetweenDictionaries()函数是这样的：

function [betterDictionaryElement,CoefMatrix,NewVectorAdded] = I_findBetterDictionaryElement(Data,Dictionary,j,CoefMatrix,numCoefUsed)
relevantDataIndices = find(CoefMatrix(j,:));
 % 查找出系数矩阵中每一行中非0元素的序号，即使用了第j个原子的的序号
if (length(relevantDataIndices)<1) %(length(relevantDataIndices)==0)  %如果系数矩阵为空，则进行如下的语句 。 如果relevantDataIndices为0，说明没有patch表达需要用到第j个原子，则执行以下语句，称为语句块1
    ErrorMat = Data-Dictionary*CoefMatrix;
    ErrorNormVec = sum(ErrorMat.^2);
    [d,i] = max(ErrorNormVec);
    betterDictionaryElement = Data(:,i);
    betterDictionaryElement = betterDictionaryElement./sqrt(betterDictionaryElement'*betterDictionaryElement);%归一化
    betterDictionaryElement = betterDictionaryElement.*sign(betterDictionaryElement(1));
    CoefMatrix(j,:) = 0;
    NewVectorAdded = 1%%%%%实验证明（针对w.jpg图像），值累加了一次
%     liuzhe=1  没进行此句，说明稀疏矩阵的每一行都有非零的元素
    return;
end
%如果length(relevantDataIndices)不为0，也就是说有patch的表达使用到了第j个原子，则执行以下语句，称为语句块2
NewVectorAdded = 0;
tmpCoefMatrix = CoefMatrix(:,relevantDataIndices); %将稀疏矩阵中使用了第j个原子的系数向量取出来，tmpCoefMatrix尺寸为：256*length(relevantDataIndices)
tmpCoefMatrix(j,:) = 0;% the coeffitients of the element we now improve are not relevant.
errors =(Data(:,relevantDataIndices) - Dictionary*tmpCoefMatrix); % vector of errors that we want to minimize with the new element    D:64*256     tmpCoefMatrix尺寸为：256*length(relevantDataIndices)  Data(:,relevantDataIndices):64*relevantDataIndices
%%在这里使用SVD就可以达到|| errors - beta*element ||_F^2误差最小的效果
[betterDictionaryElement,singularValue,betaVector] = svds(errors,1);%%%%%%%仅仅取出了第一主分量，betterDictionaryElement*singularValue*betaVector'近似的可以表示errors
CoefMatrix(j,relevantDataIndices) = singularValue*betaVector';%这里把SVD向量的左奇异矩阵的第一主向量作为更新的字典原子dk，把奇异值和右奇异向量的第一主向量的乘积作为更新的稀疏向量xk

对I_findDistanseBetweenDictionaries()函数进行分析：

如果上一次迭代中没有任何图像块的系数表示使用过第j个原子，则if语句条件成立，那么利用上一次的稀疏矩阵计算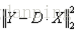并把误差最大的一项（第i项）提取出来，并把原始数据中的对应的Data(:,i)作为更新的原子，这样做的原因是把Data(:,i)作为更新的原子，这样就把最大误差消除为0.

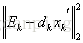
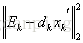
如果上一次迭代中使用过第j个原子，也就是if条件不成立，那么就执行语句块2，在语句块2中，把上一次迭代中使用了第j个原子的xk提取出来，并且计算，利用SVD算法可以得到的最小二乘解，并把SVD算法的左奇异矩阵的第一主向量作为更新的字典原子dk，把右奇异矩阵的第一主向量和最大的奇异值的乘积作为更新的稀疏向量xk。

以下是有详细注释的程序

denoiseImageKSVD.m


 
 
 
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     function [IOut,output] = denoiseImageKSVD(Image,sigma,K,varargin)
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %==========================================================================
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %   P E R F O R M   D E N O I S I N G   U S I N G   A  D I C T  I O N A R Y
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                  T R A I N E D   O N   N O I S Y   I M A G E
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %==========================================================================
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     % function IOut = denoiseImageKSVD(Image,sigma,K,varargin)
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     % denoise an image by sparsely representing each block 
     
     
     with the
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     % already overcomplete trained Dictionary, 
     
     
     and averaging the represented parts.
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     % Detailed description can be found 
     
     
     in 
     
     
     "Image Denoising Via Sparse and Redundant
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     % representations over Learned Dictionaries", (appeared 
     
     
     in the 
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     % IEEE Trans. on Image Processing, Vol. 
     
     
     15, no. 
     
     
     12, December 
     
     
     2006).
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     % This function may take some time to process. Possible factor that effect
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     % the processing time are:
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %  
     
     
     1. number of KSVD iterations - the default number of iterations 
     
     
     is 
     
     
     10.
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %  However, fewer iterations may, 
     
     
     in most cases, result an acceleration 
     
     
     in
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %  the process, without effecting  the result too much. Therefore, when
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %  required, this parameter may be re-set.
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %  
     
     
     2. maxBlocksToConsider - The maximal number of blocks to train on. If this 
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %  number 
     
     
     is larger the number of blocks 
     
     
     in the image, random blocks
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %  
     
     
     from the image will be selected 
     
     
     for training. 
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     % ===================================================================
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     % INPUT ARGUMENTS : Image - the noisy image (gray-level scale)
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                   sigma - the s.d. of the noise (assume to be white Gaussian).
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                   K - the number of atoms 
     
     
     in the trained dictionary.
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %    Optional arguments:              
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                  
     
     
     'blockSize' - the size of the blocks the algorithm
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       works. All blocks are squares, therefore the given
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       parameter should be one number (width 
     
     
     or height).
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       Default value: 
     
     
     8.
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       
     
     
     'errorFactor' - a factor that multiplies sigma 
     
     
     in order
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       to set the allowed representation error. In the
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       experiments presented 
     
     
     in the paper, it was set to 
     
     
     1.15
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       (which 
     
     
     is also the default  value here).
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                  
     
     
     'maxBlocksToConsider' - maximal number of blocks that
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       can be processed. This number 
     
     
     is dependent on the memory
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       capabilities of the machine, 
     
     
     and performances?
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       considerations. If the number of available blocks 
     
     
     in the
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       image 
     
     
     is larger than 
     
     
     'maxBlocksToConsider', the sliding
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       distance between the blocks increases. The default value
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       
     
     
     is: 
     
     
     250000.
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                  
     
     
     'slidingFactor' - the sliding distance between processed
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       blocks. Default value 
     
     
     is 
     
     
     1. However, 
     
     
     if the image 
     
     
     is
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       large, this number increases automatically (because of
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       memory requirements). Larger values result faster
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       performances (because of fewer processed blocks).
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                  
     
     
     'numKSVDIters' - the number of KSVD iterations processed
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       blocks 
     
     
     from the noisy image. If the number of
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       blocks 
     
     
     in the image 
     
     
     is larger than this number,
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       random blocks 
     
     
     from all available blocks will be
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       selected. The default value 
     
     
     for this parameter 
     
     
     is:
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       
     
     
     10 
     
     
     if sigma > 
     
     
     5, 
     
     
     and 
     
     
     5 otherwise.
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                  
     
     
     'maxNumBlocksToTrainOn' - the maximal number of blocks
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       to train on. The default value 
     
     
     for this parameter 
     
     
     is
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       
     
     
     65000. However, it might 
     
     
     not be enough 
     
     
     for very large
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       images
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                  
     
     
     'displayFlag' - 
     
     
     if this flag 
     
     
     is switched on,
    
    
    
   
   
   
  
   
   
   
    
    
    
   
   
   
   
   
   
    
    
    
     
     
     %                       announcement after finishing each it

稀疏表示（二）——KSVD算法详解（结合代码和算法思路）

稀疏表示（二）——KSVD算法详解（结合代码和算法思路）

悦读