文章目录
前言
贪心算法,如同成语"得陇望蜀"所描述的那样,总是追求眼前的最优选择,渴望在每一步都获得最大的利益。虽然这种策略在某些情况下能够高效地找到满意解,但它也有可能忽视了长期目标,从而无法达到全局最优。
学习路线:C++从入门到NOI学习路线
学习大纲:C++全国青少年信息学奥林匹克竞赛(NOI)入门级-大纲
一、概念
1.导入
想要学会贪心算法,就得理解贪心的本质——“贪”。
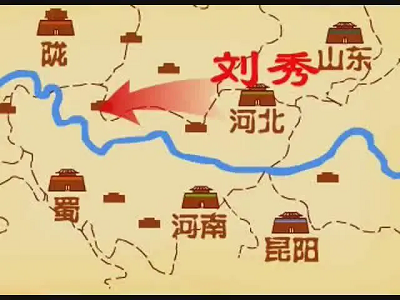
东汉初年,有两股反对光武帝的地方势力:一是割据巴蜀的公孙述;二是称霸陇西(今甘肃东部)的隗嚣。
哦,隗嚣(wěi xiáo)。
光武帝刘秀派遣大将岑彭(cén péng)去攻打陇地(今甘肃一带);
岑彭(cén péng)不负众望,成功占领了陇地,为刘秀立下了赫赫战功。
然而,就在众人以为可以稍作休整之时,刘秀却并未满足于此。他心中有着更大的图谋——蜀地(今四川一带),那个物产丰富、地势险要的宝地。于是,刘秀在给岑彭的书信中写道:“人苦不知足,既平陇,复望蜀。”
刘秀的这句话,其实与我们今天要学习的贪心算法有着异曲同工之妙。
2.概念
贪心算法,顾名思义,就是在每一步选择中都采取当前状态下最好或最优的选择,从而希望导致结果是全局最好或最优的算法策略。
它就像刘秀一样,总是追求着更大的目标,不满足于现状,不断向前探索。
2.1 贪心算法的核心思想
-
局部最优选择:在每一步,算法都做出一个当前看来最好的选择(即最有利的选择),这个选择仅依赖于当前状态,而不考虑未来可能的状态或选择。
-
全局最优解:尽管贪心算法每一步都做出局部最优选择,但它并不保证能得到全局最优解。然而,对于某些特定类型的问题,贪心算法能够确保找到全局最优解。
-
无后效性:即贪心选择一旦确定,就不会再改变。这是因为贪心算法做出的选择是基于当前状态的最优选择,一旦状态改变(比如选择了某个元素后),之前的选择就不再考虑。
-
不可逆性:选择一旦做出,就无法撤销,即算法的每一步决策都是确定性的,没有回溯机制。
-
最优子结构:如果一个问题的最优解包含其子问题的最优解,则称该问题具有最优子结构性质。贪心算法通常适用于具有最优子结构的问题。
2.2 贪心算法的步骤
-
定义问题与选择标准:
- 清晰定义问题的目标(如最小化、最大化)。
- 确定贪心选择的标准,即每一步选择当前状态下的最优解的依据。
-
逐步构建解:
- 从初始状态开始,按照贪心选择标准逐步构建问题的解。
- 在每一步选择中,只考虑当前状态,不考虑未来的影响。
-
得到最终解:
- 当无法再进行贪心选择时(如所有元素都已处理完毕),算法结束。
- 此时得到的解即为问题的贪心解(可能是全局最优解,也可能是局部最优解)。
2.3 贪心算法的应用场景
- 集合覆盖问题
- 场景描述:有一些广播台,每个广播台可以覆盖一些地区,目标是选择最少的广播台以覆盖所有地区。
- 贪心策略:在每一步中,选择能覆盖最多尚未覆盖地区数的广播台加入到最终的覆盖集合中,直到所有地区都被覆盖。
- 分数背包问题
- 场景描述:有一个固定容量的背包,以及一系列具有不同重量和价值的物品,目标是选择一些物品装入背包,使得背包中的物品总价值最大,同时总重量不超过背包的容量。特别地,当物品可以分割时,贪心算法可以得到最优解。
- 贪心策略:计算物品的单位价值(价值除以重量),并按照单位价值从高到低排序,然后依次选择物品直至背包容量达到极限。
- 旅行商问题(TSP)
- 注意:虽然旅行商问题本身是一个NP难问题,但在某些特定情况或近似解法中,贪心算法可以被用来寻找近似解。
- 贪心策略:可能包括选择最近的城市作为下一个访问点,但这种策略并不保证得到全局最短路径,只是提供了一个可行的解。
- 区间调度问题
- 场景描述:一个工厂有许多订单需要进行生产,每个订单都有一个开始时间和结束时间,目标是找出一种生产顺序,使得能够完成尽可能多的订单。
- 贪心策略:总是选择结束时间最早且不与已选订单冲突的订单进行生产,这样可以最大化可接受订单的数量。
- 最小生成树问题
- 场景描述:在无向图中,找到一棵边权和最小的生成树。
- 贪心算法应用:Prim算法和Kruskal算法都是贪心算法在最小生成树问题中的应用。Prim算法从任意顶点开始,逐步增加边和顶点,直到形成最小生成树;Kruskal算法则按照边的权重从小到大排序,逐步增加边,同时避免形成环。
- 最短路径问题
- 场景描述:在图中找到从一个顶点到另一个顶点的最短路径。
- 贪心算法应用:在Dijkstra算法中,贪心算法被用来寻找单源最短路径。Dijkstra算法通过逐步扩展已找到最短路径的顶点集合,并更新其他顶点的最短路径,直到找到目标顶点为止。
- 活动选择/任务调度问题
- 场景描述:有一系列活动(或任务),每个活动都有开始和结束时间,且同一时间只能进行一个活动,目标是选择尽可能多的互不冲突的活动。
- 贪心策略:总是选择结束时间最早的活动,一旦活动结束,就立即开始下一个最早结束的活动,这样可以最大化可接受活动的数量。
- 霍夫曼编码
- 场景描述:在信息编码中,为了节省存储空间或传输时间,需要对数据进行压缩。
- 贪心算法应用:霍夫曼编码使用贪心算法构建霍夫曼树,将出现频率较高的字符用较短的编码表示,频率较低的字符用较长的编码表示,从而实现数据的高效压缩。
- 硬币找零问题
- 场景描述:使用最少数量的硬币来凑出目标金额。
- 贪心策略:从面值最大的硬币开始,尽可能多地使用它,然后转向下一个较小的面值,直到凑出目标金额。需要注意的是,这种方法在某些货币体系下可能不会得到最优解,例如美国货币体系中,对于4美分的情况,直接使用4个1美分硬币比使用1个5美分硬币和1个1美分硬币要更少,但这种情况在实际中并不常见。
- 最优二叉搜索树(Optimal Binary Search Tree)
- 场景描述:给定一系列关键字及其访问概率,构造一棵二叉搜索树,使得查找操作的平均成本最小。这里的成本可以理解为查找过程中经过的节点数,而平均成本则是对所有关键字查找的成本按概率加权求和。
- 贪心算法应用:尽管直观上可能会尝试贪心策略,比如先插入访问概率最高的关键字,但实际上最优二叉搜索树问题并不适合直接使用简单的贪心算法解决。动态规划方法是解决该问题的标准手段,因为它需要考虑全局最优而非局部最优。然而,在某些特定情况下,如果所有关键字的访问概率相同,则构建平衡的二叉搜索树(如AVL树或红黑树)可以看作是一种“贪心”策略,即在每次插入时尽量保持树的平衡,从而最小化查找深度。
- 文件合并问题(File Merge Problem)
- 场景描述:一组文件需要被合并成一个大文件。每次合并两个文件时,产生的开销等于两个文件的大小之和。目标是最小化合并所有文件的总开销。
- 贪心策略:在每一步中,选择当前最小的两个文件进行合并。这一策略保证了每次合并产生的额外开销都是最小的,从而最小化了总的合并成本。这个过程可以通过优先队列(堆)来高效实现,每次取出两个最小元素进行合并,再将合并后的新文件放回队列中,直到所有文件被合并成一个。
二、例题讲解
问题:1372. 活动选择
类型:贪心
题目描述:
学校在最近几天有 n(n≤100)个活动,这些活动都需要使用学校的大礼堂,在同一时间,礼堂只能被一个活动使。由于有些活动时间上有冲突,学校办公室人员只好让一些活动放弃使用礼堂而使用其他教室。
现在给出 n 个活动使用礼堂的起始时间begini 和结束时间 endi (begini < endi),请你帮助办公室人员安排一些活动来使用礼堂,要求安排的活动尽量多。请问最多可以安排多少活动?
请注意,开始时间和结束时间均指的是某个小时的 0 分 0 秒,如:3 5,指的是 3:00~5:00 ,因此3 5和5 9这两个时间段不算冲突的时间段。
输入:
第一行一个整数 n (n≤100);
接下来的 n 行,每行两个整数,第一个 begini ,第二个是 endi (begini < endi ≤ 32767);
输出:
输出最多能安排的活动数;
样例:
输入:
11
3 5
1 4
12 14
8 12
0 6
8 11
6 10
5 7
3 8
5 9
2 13
输出:
4
解题思路:
首先,我们需要清晰地理解问题的要求:给定一系列活动,每个活动都有一个开始时间和一个结束时间,我们需要找出一种安排方式,使得在任意时刻最多只有一个活动在进行,同时尽可能多地安排活动。
本题的关键在于采用贪心策略,即首先根据活动的结束时间对它们进行排序,然后依次检查每个活动是否能被安排而不与前一个已安排的活动冲突(即检查当前活动的开始时间是否晚于前一个活动的结束时间)。通过这种方法,我们可以确保在遵守时间约束的前提下,最大化可安排的活动数量。最后,输出这个最大数量作为答案。
1.分析问题
- 已知:有 n(n≤100)个活动, n 个活动使用礼堂的起始时间begini 和结束时间 endi (begini < endi)。
- 未知:请问最多可以安排多少活动?
- 关系:采用贪心策略,关键在于按活动的结束时间进行排序。
2.定义变量
//二、数据定义
int n,a[1010],b[1010],endi=0,c=0;
3.输入数据
//三、数据输入
cin>>n;
for(int i=0;i<n;i++){
cin>>a[i]>>b[i];
}
4.数据计算
- 使用冒泡排序算法对活动的结束时间进行升序排序。在交换结束时间的同时,同步交换对应的开始时间,以保持活动信息的完整性。
for(int i=0;i<n-1;i++){
for(int j=0;j<n-1-i;j++){
if(b[j]>=b[j+1]){
swap(b[j],b[j+1]);
//同步开始时间
swap(a[j],a[j+1]);
}
}
}
- 选择不冲突活动:遍历排序后的活动列表,如果当前活动的开始时间大于等于endi(即前一个活动的结束时间),说明当前活动可以安排,此时更新endi为当前活动的结束时间,并增加已安排活动计数器c。
for(int i=0;i<n;i++){
if(a[i]>=endi){
endi=b[i];
++c;
}
}
5.输出结果
- 输出最多能安排的活动数量。
cout << c << endl;
完整代码如下:
#include<bits/stdc++.h>
using namespace std;
int main(){
// 一、问题分析
// 给定多个活动,每个活动由起始时间和结束时间定义,要求计算并输出最多能安排多少个活动,
// 条件是活动不能同时进行,即一个活动开始时,前一个活动必须已经结束。
// 解决方案采用贪心策略,关键在于按活动的结束时间进行排序。
// 二、数据定义
int n; // 活动数量
int a[1010], b[1010]; // a[] 存储活动的开始时间,b[] 存储活动的结束时间
int begini, endi = 0; // begini 临时存储活动的开始时间,endi 记录当前已安排活动的最晚结束时间
int c = 0; // c 记录最多可以安排的活动数量
// 三、数据输入
cin >> n; // 输入活动数量
for(int i = 0; i < n; i++) {
cin >> a[i] >> b[i]; // 输入每个活动的开始时间和结束时间
}
// 四、数据处理 - 按结束时间排序活动
// 冒泡排序算法,保证b[](结束时间数组)升序排列,同时同步调整a[](开始时间数组)
for(int i = 0; i < n - 1; i++) {
for(int j = 0; j < n - 1 - i; j++) {
if(b[j] >= b[j+1]) { // 发现逆序则交换
swap(b[j], b[j+1]); // 交换结束时间
swap(a[j], a[j+1]); // 同步交换开始时间,保持活动信息对应
}
}
}
// 五、根据排序后的活动选择不冲突的活动
for(int i = 0; i < n; i++) {
if(a[i] >= endi) { // 当前活动的开始时间大于等于上一个活动的结束时间,说明不冲突
endi = b[i]; // 更新最晚结束时间为当前活动的结束时间
++c; // 可以安排此活动,活动数量加一
}
}
// 六、输出结果
cout << c << endl; // 输出最多能安排的活动数量
return 0; // 程序正常结束
}
问题:1456. 淘淘捡西瓜
类型:贪心
题目描述:
地上有一排西瓜,每个西瓜都有自己的重量。淘淘有一个包,包的容量是固定的,淘淘希望尽可能在包里装更多的西瓜(当然要装整个的,不能切开装),请问淘淘的包最多能装下多少个西瓜?
输入:
第一行两个整数n,x ,表示有 n 个西瓜,背包容量是x 。( 1∼n∼100 ) 下面 n 个整数,表示西瓜的重量。
输出:
一个整数,表示淘淘最多能装多少西瓜回家。
样例:
输入:
5 10
2 3 1 5 4
输出:
4
解题思路:
解题的关键在于运用贪心算法优化西瓜装包过程。
即在每一步都做出局部最优选择(优先装入轻的西瓜),以期达到全局最优解(装入最多的西瓜)。
首先,读取西瓜的数量和背包的容量,并收集每个西瓜的重量信息。接着,对西瓜重量进行排序,确保能优先考虑轻的西瓜。
随后,遍历排序后的西瓜列表,每次尝试装入一个西瓜,如果装入后背包容量仍然足够,则更新背包剩余容量并增加已装西瓜数量计数;一旦发现当前西瓜无法装入,即表明后续更重的西瓜也无法装入,此时可立即终止。
1.分析问题
- 已知:n 个西瓜,背包容量是x。
- 未知:表示淘淘最多能装多少西瓜回家。
- 关系:贪心。
2.定义变量
- 定义了整型变量n(西瓜总数)、x(背包容量)、整型数组a[110](存放每个西瓜的重量)和整型变量c(计数器,表示能装入的西瓜数量)。
//二、数据定义
int n,x,a[110],c=0;
3.输入数据
- 读取西瓜总数n和背包容量x,随后读取每个西瓜的重量。
//三、数据输入
cin>>n>>x;
for(int i=0;i<n;i++){
cin>>a[i];
}
4.数据计算
- 首先使用sort(a, a+n)对西瓜重量进行升序排序。
- 接着,遍历排序后的西瓜数组,对于每个西瓜,如果其重量加上当前背包已有的物品重量不超过总容量x,就将该西瓜装入背包(减去西瓜重量x -= a[i]),并累加西瓜计数c++。
- 如果某西瓜无法装入(即x-a[i]<0),则直接跳出循环,因为后面的西瓜更重,也不可能装入。
//四、数据计算
sort(a,a+n);
for(int i = 0; i < n; i++) {
// 如果当前西瓜重量加上已装西瓜总重量不超过背包容量
if(x - a[i] >= 0) {
x -= a[i]; // 减去当前西瓜的重量,模拟装入背包
++c; // 成功装入一个西瓜,计数加一
} else {
// 若当前西瓜不能装入,直接终止循环,因为后面的西瓜更重,也无法装入
break;
}
}
5.输出结果
- 输出能装入背包的最大西瓜数量c。
//五、输出结果
cout<<c;
return 0;
完整代码如下:
#include<bits/stdc++.h>
using namespace std;
int main(){
// 一、问题分析
// 面临问题:有n个西瓜,每个西瓜有不同的重量,需要将这些西瓜放入一个容量为x的背包中。
// 目标:确定在不超过背包容量的前提下,淘淘最多能携带多少个西瓜回家。
// 方法:采用贪心策略,优先选择重量轻的西瓜装入背包。
// 二、数据定义
int n, x; // n: 西瓜总数, x: 背包容量
int a[110]; // a[]: 存储每个西瓜的重量
int c = 0; // c: 记录能装入背包的西瓜数量
// 三、数据输入
cin >> n >> x; // 输入西瓜总数和背包容量
for(int i = 0; i < n; i++) {
cin >> a[i]; // 输入每个西瓜的重量
}
// 四、数据处理 - 贪心策略选择西瓜
// 首先对西瓜重量进行升序排序,确保先考虑轻的西瓜
sort(a, a + n);
// 遍历排序后的西瓜数组
for(int i = 0; i < n; i++) {
// 如果当前西瓜重量加上已装西瓜总重量不超过背包容量
if(x - a[i] >= 0) {
x -= a[i]; // 减去当前西瓜的重量,模拟装入背包
++c; // 成功装入一个西瓜,计数加一
} else {
// 若当前西瓜不能装入,直接终止循环,因为后面的西瓜更重,也无法装入
break;
}
}
// 五、输出结果
cout << c; // 输出能装入背包的西瓜数量
return 0; // 程序正常结束
}
问题:1551 - 任务调度
类型:2017江苏省青少年信息学奥林匹克竞赛复赛、贪心
题目描述:
乌龟因为动作太慢,有 n 个任务已经超过截止日期了。乌龟处理第 i 个任务需要 ai 单位时间。从 0 时刻开始,乌龟可以选择某项任务,完成它,然后再开始另一项任务,如此往复直到所有任务都被完成。
由于已经超过截止日期,乌龟会为此受到一定的惩罚,惩罚值等于所有任务完成时刻之和。例如,有 2 个任务分别需要 10 和 20 单位时间完成。如果先完成任务 1,惩罚值为 10+30=40;如果先完成任务 2,惩罚值为20+30=50 。
乌龟希望你求出惩罚值最小的完成任务的顺序。
输入:
两个整数 n, R1,表示任务的数量和生成数列的首项。
处理任务i (1≤i≤n) 的时间 ai=(Ri mod100)+1。
试题中使用的生成数列 R 定义如下:整数0≤R1<20170 在输入中给出。对于i>1,Ri=(R(i−1)×6807+2831)mod20170。
输出:
一个整数,表示完成所有任务的最小惩罚值。
样例:
输入:
10 2
输出:
1771
解题思路:
解决这个问题的核心在于认识到惩罚值与任务完成顺序的关系。
惩罚值由所有任务完成时刻之和构成,而每个任务的完成时刻取决于它前面有多少任务已完成以及这些任务的总耗时。
因此,为了最小化惩罚值,应该尽可能地减少后面任务的等待时间,这意味着要优先处理耗时较短的任务。
1.分析问题
- 已知:有 n 个任务,ri生成数列的首项。
- 未知:求出惩罚值最小的完成任务的ai的总和。
- 关系:处理任务i (1≤i≤n) 的时间 ai=(Ri mod100)+1。对于i>1,Ri=(Ri-1×6807+2831)mod20170。
2.定义变量
- 定义变量n、ai、ri、temp和result以及一个存储任务完成时间的向量v。
//二、数据定义
long long int n,ai,ri,temp=0,result=0;
vector<int> v;
3.输入数据
- 从标准输入读取n和ri的值。
- 使用循环计算每个任务的完成时间ai,并将其存入向量v。
//三、数据输入
cin>>n>>ri;
for(int i=0;i<n;i++){
ai=(ri%100)+1;
v.push_back(ai);
ri=(ri*6807+2831)%20170;
}
4.数据计算
- 对v中的元素进行排序(从小到大)。
- 再次循环遍历v中的元素,计算累积的任务完成时间和总惩罚值result。
//四、数据计算
sort(v.begin(),v.end());
for (int i = 0; i < n; ++i) {
result += v[i] * (n - i);
}
5.输出结果
- 输出最终的总惩罚值result。
//五、输出结果
cout<<result;
return 0;
完整代码如下:
#include<bits/stdc++.h>
using namespace std;
int main(){
//一、分析问题
//已知:有 n 个任务,ri生成数列的首项。
//未知:求出惩罚值最小的完成任务的ai的总和.
//关系:处理任务i (1≤i≤n) 的时间 ai=(Ri mod100)+1。对于i>1,Ri=(Ri-1×6807+2831)mod20170。
int n, ri; // 定义变量n和ri
cin >> n >> ri; // 从标准输入读取n和ri的值
vector<int> v(n); // 定义一个大小为n的整型向量v
int ai, temp = ri; // 定义变量ai和temp,temp初始化为ri
long long result = 0; // 定义并初始化结果变量result
// 计算每个任务的完成时间ai,并存入向量v
for (int i = 0; i < n; ++i) {
ai = (temp % 100) + 1; // 计算当前任务的完成时间
v[i] = ai; // 将ai存入向量v的第i个位置
temp = (temp * 6807 + 2831) % 20170; // 更新temp
}
sort(v.begin(), v.end()); // 对向量v中的元素进行排序
// 计算累积的任务完成时间和总惩罚值result
for (int i = 0; i < n; ++i) {
result += v[i] * (n - i); // 累加每个任务的惩罚值
}
cout << result << endl; // 输出最终的总惩罚值result
return 0;
}
问题:1561. 买木头
类型:省赛、数组问题、二分答案、贪心、2015江苏省青少年信息学奥林匹克竞赛复赛
题目描述:
有 n 个木材供应商,每个供货商有长度相同一定数量的木头。长木头可以锯短,但短木头不能接长。有一个客人要求 m 根长度相同的木头。要求计算出,此时供货商提供的木头满足客人要求的最长的长度是多少。
例如 n=2,m=30,两个供货商的木头为
12,10 第 1 个供货商的木头长度为 12 ,共有 10 根;
5,10 第 2 个供货商的木头长度为 5 ,共有 10 根。
计算的结果为 5 ,即长度为 12 的木头一根可锯出两根长度为 5 的木头,多余的无用,长度为 5 的木头不动,此时可得到 30 根长度为 5 的木头。
输入:
整数 n,m,L1,S1 (1≤n≤10000,1≤m≤1000000,1≤L1≤10000,1≤S1≤100)
其中 L1 是第一个供货商木头的长,S1 是第一个供货商木头数量。其他供货商木头的长度和数量 Li 和 Si(i≥2),由下面的公式给出:
Li=((Li−1×37011+10193)mod10000)+1
Si=((Si−1×73011+24793)mod100)+1
输出:
一个整数,即满足要求的 m 根长度相同的木头的最大长度。
样例:
输入:
10 10000 8 20
输出:
201
解题思路:
解题的核心是运用二分查找算法来确定能够满足顾客需求的木头最大长度。首先,通过题目给定的序列生成规则,构建出所有供应商的木头长度和库存量。然后,设定一个查找区间,该区间上限为理论上木头可能的最大长度,下限为最小可能的长度(即1)。通过反复折半这个区间并检查中间值是否能使所有供应商提供的木头总和达到或超过顾客所需数量,逐步缩小范围直到找到确切的最大长度。这一过程中,如果中间值能满足需求,则证明存在更长的可能性,于是更新下界;反之,若不满足则表明需要更短的长度,从而更新上界。最终,当上下界收敛于同一数值时,该值即为所求的最大长度。
1.分析问题
-
已知:有n个木材供应商。需要m 根长度相同的木头。L 是第一个供货商木头的长,S是第一个供货商木头数量。
-
未知:供货商提供的木头满足客人要求的最长的长度是多少。
-
关系:长木头可以锯短,但短木头不能接长。其他供货商木头的长度和数量 Li 和 Si(i≥2),由下面的公式给出:Li=((Li-1×37011+10193)mod10000)+1、Si=((Si-1×73011+24793)mod100)+1
2.定义变量
- m: 需要的木头数量。
- cmax: 最长木头长度。
- v: 保存所有木头长度的向量。
int m, cmax = 0;
vector<int> v;
3.输入数据
- 输入供应商数量 n,需要的木头数量 m,第一个供应商的木头长度 li 和数量 si。
- 循环遍历所有供应商,将所有木头长度加入向量 v,同时计算后续供应商的木头长度和数量。
//三、数据输入
cin>>n>>m>>li>>si;
for(int i=0;i<n;i++){
for(int j=0;j<si;j++){
v.push_back(li);
}
li=(li*37011+10193)%10000+1;
si=(si*73011+24793)%100+1;
}
4.数据计算
- 对木头长度向量进行降序排序。
- 调用 myFind 函数进行二分查找,确定最长木头长度。
//四、数据计算
sort(v.begin(),v.end(),cmp);
myFind(1,v[0]);
- 自定义的比较函数,用于将绳子长度按降序排列。在C++中,sort()函数默认按升序排序,使用此函数可以改变排序方式。
bool cmp(int a,int b){
return a>b;
}
- findNum函数用于计算在给定长度mid下,所有木头能切割出多少段长度为mid的木头段。它遍历每根木头,检查其能贡献多少段长度为mid的木头段,然后返回这些段的总数。
int findNum(int mid){
int c=0,t;
for(int i=0;i<v.size();i++){
t=v[i];
while(t>=mid){
++c;
t-=mid;
}
}
return c;
}
- myFind函数使用二分查找法来寻找满足条件的木头段最大长度。它首先检查当前搜索区间的有效性,然后计算区间的中点mid。接下来,它使用findNum函数来检查在长度为mid的情况下能否切割出至少m段木头。如果不能,搜索区间变为[l, mid-1];如果可以,更新cmax为mid,并且搜索区间变为[mid+1, r]。这一过程重复,直到找到满足条件的最大长度。
void myFind(int l,int r){
if(l>r){
return;
}
int mid;
mid=l+r>>1;
if(m>findNum(mid)){
return myFind(l,mid-1);
}else{
cmax=mid;
return myFind(mid+1,r);
}
}
5.输出结果
- 输出最长木头长度。
//五、输出结果
cout<<cmax;
完整代码如下:
#include<bits/stdc++.h>
using namespace std;
int m, cmax = 0; // m: 需要的木头数量, cmax: 最长木头长度
vector<int> v; // 存储所有木头的长度
// 比较函数,用于对木头长度进行降序排列
bool cmp(int a, int b){
return a > b;
}
// 计算在给定长度下,所有木头可以被切成多少段
int findNum(int mid){
int count = 0, temp;
for(int i = 0; i < v.size(); i++){
temp = v[i];
while(temp >= mid){
++count;
temp -= mid;
}
}
return count;
}
// 使用二分查找确定最长木头长度
void myFind(int left, int right){
if(left > right){
return;
}
int mid = (left + right) / 2; // 计算中间值
if(m > findNum(mid)){ // 如果当前长度下的木头数量不足
return myFind(left, mid - 1); // 在左半边继续查找
}else{
cmax = mid; // 更新最长木头长度
return myFind(mid + 1, right); // 在右半边继续查找
}
}
int main(){
//1. 已知:有n个木材供应商。需要m 根长度相同的木头。L 是第一个供货商木头的长,S是第一个供货商木头数量。
//2. 未知:供货商提供的木头满足客人要求的最长的长度是多少。
//3. 关系:长木头可以锯短,但短木头不能接长。其他供货商木头的长度和数量 Li 和 Si(i≥2),由下面的公式给出:Li=((Li-1×37011+10193)mod10000)+1、Si=((Si-1×73011+24793)mod100)+1
// 数据定义
int n, t, li, si;
// 数据输入
cin >> n >> m >> li >> si; // 输入供应商数量、需要的木头数量、第一个供应商的木头长度和数量
for(int i = 0; i < n; i++){
for(int j = 0; j < si; j++){
v.push_back(li); // 将当前供应商的所有木头长度加入到向量中
}
li = (li * 37011 + 10193) % 10000 + 1; // 计算下一个供应商的木头长度
si = (si * 73011 + 24793) % 100 + 1; // 计算下一个供应商的木头数量
}
// 数据计算
sort(v.begin(), v.end(), cmp); // 对木头长度进行降序排序
myFind(1, v[0]); // 开始二分查找
// 输出结果
cout << cmax; // 输出最长木头长度
return 0;
}
三、总结
贪心算法的执行效率通常较高,因为它避免了穷举搜索和回溯,但是其正确性和有效性高度依赖于问题本身是否具备贪心选择性质和最优子结构性质。如果问题满足这些性质,那么贪心算法可以快速找到最优解;否则,它可能只能给出近似解,甚至是次优解。因此,在设计和应用贪心算法时,验证这些问题是非常重要的。
五、感谢
如若本文对您的学习或工作有所启发和帮助,恳请您给予宝贵的支持——轻轻一点,为文章点赞;若觉得内容值得分享给更多朋友,欢迎转发扩散;若认为此篇内容具有长期参考价值,敬请收藏以便随时查阅。
每一次您的点赞、分享与收藏,都是对我持续创作和分享的热情鼓励,也是推动我不断提供更多高质量内容的动力源泉。期待我们在下一篇文章中再次相遇,共同攀登知识的高峰!