移位运算
在十进制数字中,将小数点往右移动n位,则相当于把数字乘上10的n次方,同理,往左移动n位相当于除以10的n次方
移位运算是指通过改变各个数码位和小数点的相对位置,从而改变各数码位权
在r进制数中,把小数点往右移动n位相当于把原来的数乘上r的n次方,而往左移动n位相当于除以r的n次方。通过移位的方法可以实现乘除运算
原码的算数移位
将原码算数移位,是指符号位不变,将后面的数字进行移位,不足处补0,低位直接舍弃
例如26的原码是 "00011010",将该原码算数右移一位,得到 "00001101",十进制为13
将数字算数右移n位,相当于把小数点左移n位,因此得到的数字是原本的1/2
若将上面的原码继续算数右移,得到 "00000110",此时最低位被舍弃,得到的数字为6,因此当舍弃位不为0时,会丢失精度
反码的算数移位
正数的反码与原码相同,因此对于正数的算数移位与原码规律相同
负数反码的数值位与原码相反,而原码的不足处补0,因此负数反码不足处补1
补码的算数移位
与反码同理,正数补码的算数位移运算与原码规律相同
负数补码是通过反码最低位加一得到的
例如补码 "11101100",显然它的反码是 "11101011",补码中的最后一个1是由反码加一进位得到的,而负数反码的算数移位是补1,因此负数补码的右边应该补0
在负数补码最后一个1的左边,仍然是与反码相同的,因此左边应该补1
总结上面的规律,负数补码左移补0,右移补1
逻辑移位
逻辑移位的规则很简单,逻辑移位不区分符号位和数值位,而是把全部位共同左移和右移,并且不足处一律补0,它可以看成一个无符号数的移位
循环移位
顾名思义,循环移位就是把多出来的位补到不足处的位
当数字带有进位位时,进位位应该与整个数值位一同参与移位
考点总览
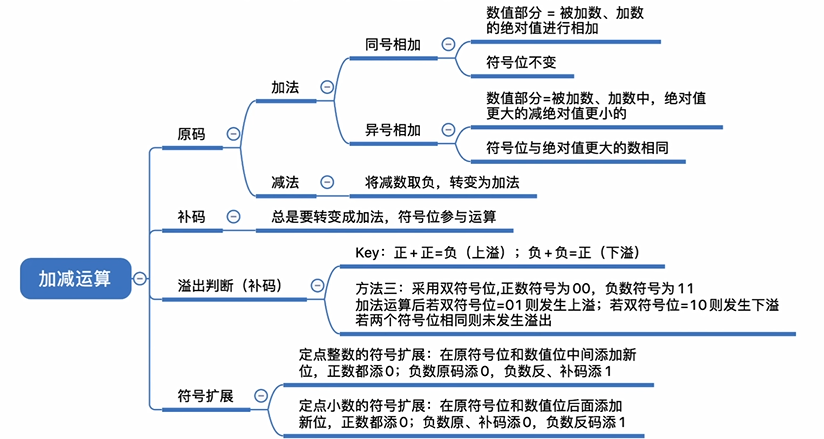
加减运算
原码的加减
原码的加减运算可以类似地看成十进制数的加减运算
无论是加减,都需要把两个数全部换成正数,例如 1 + (-2) 需要换成 1 - 2,这是为了确保符号位统一。如果两个数都是负数,那么只需要把两数绝对值相加,结果取负即可
对于加法,直接按照十进制数的规律,逢2进1即可,对于减法,则需要用绝对值大的数减去绝对值小的数,最后符号取绝对值大的数的符号
补码的加减
补码的加减运算一律转化成加法运算,例如 1 - 2 需要转换成 1 + (-2)
求出 1 和 -2 的补码: 00000001 和 11111110。接下来连着符号位一同相加,得到 11111111,换成十进制是 -1,即是计算结果
溢出判断
在使用补码表示时,设机器字长为8位,当两个正数相加,结果超出127,则称发生了上溢;当两个负数相加,结果小于-128,则称发生了下溢
当上溢发生时,会导致两个正数相加,结果变成负数;当下溢发生时,会导致两个负数相加,结果变成正数
因此我们只需要判断符号是否出错就可以知道是否发生了溢出
逻辑判断
设第一个数的符号位为A,第二个数的符号位为B,结果的符号位为S,则我们可以使用下面的逻辑表达式判断是否发生溢出
当V为真时,则表示发生了溢出。在硬件上,只需要把逻辑运算符换成对应的门电路就能方便地实现溢出判断
进位判断
通过进位的方法也可以判断溢出。当符号位均为0,而数值位往符号位进一,则两个正数的加法运算得到了负数,发生了上溢;当符号位均为1,而数值位没有进一,则两个负数相加得到了正数,发生了下溢。因此,当符号位与数值位进位不同时,一定发生了溢出
⭐双符号位判断
前面的补码都是使用一位符号位,在这里将符号位增加到两位,且两个符号位同时为0或1
当两个正数相加时,符号位应为 00...... + 00......,此时如果数值位进一,则结果的符号位变成01,发生了上溢
当两个负数相加时,符号位应为 11...... + 11......,此时如果数值位没有进一,则结果的符号位变成10,发生了下溢
这里需要注意,双符号位数字在实际存储时只会保存一个符号位,仅仅在计算时复制一个符号位
符号扩展
为了避免溢出的发生,我们可以把一个短数据变成长数据进行运算,例如从int变成long
以8位数据变成16位数据为例
定点整数的扩展
若这个数是正数,则直接在前面加上8个0即可
若这个数是负数,则需要考虑不同的编码
对于原码,只需要把符号位移到最前面,中间填充0即可
对于反码,只需要把符号位移到最前面,中间填充1即可
对于补码,只需要把符号位移到最前面,中间填充1即可
定点小数的扩展
若这个数是正数,则直接在末尾加上8个0即可
若这个数是负数,则需要考虑不同的编码
对于原码,只需要在末尾加上8个0即可
对于反码,只需要在末尾加上8个1即可
对于补码,只需要在末尾加上8个0即可
考点总览
乘法运算
原码乘法
参考乘法的竖式运算
因此,我们只需要从乘数的最后一位开始向左遍历,如果该位为1,则加上乘数,否则加上0,然后把结果整体左移一位,直到乘数被全部遍历完成
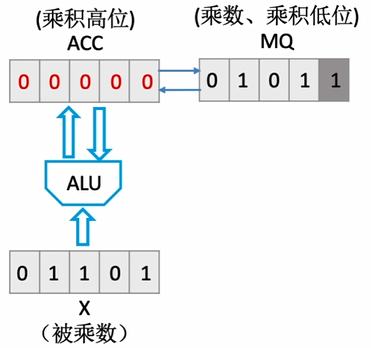
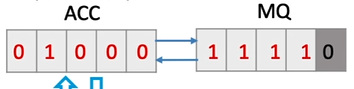
在之前的文章中,我们了解到运算器包含ACC,MQ和X。其中X用于存放被乘数,MQ用于存放乘数,ACC初始化为0
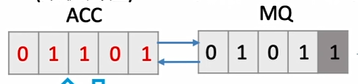
从MQ的最低位开始,若为1,则ACC加上X,若为0,则什么也不做
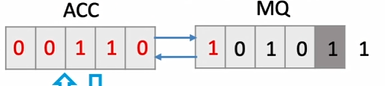
现在ACC与MQ整体右移一位,ACC的最低位移动到MQ的最高位,而ACC的最高位填充0
如此循环直到遍历完原本的MQ中的4个数(注意MQ的最高位是符号位,不参与运算),这就模拟了竖式计算中的错位相加
最后将ACC和MQ连起来,我们得到010001111,加上小数点,就是0.10001111,即结果的绝对值,结果的符号根据乘数和被乘数的符号来定
补码乘法
补码乘法与原码乘法及其类似,只有以下几点不同
补码运算时需要在MQ后面额外增加一位辅助位,且辅助位初始为0
当ACC和MQ整体右移时,MQ的最低位会被移到辅助位当中
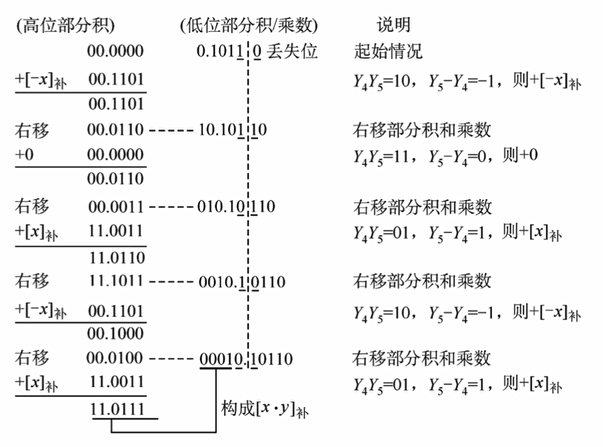
首先计算辅助位减去MQ最低位的值,以上图为例,是 0 - 1 = -1
这个计算结果可能的值有1,0,-1,则ACC应分别加上X,0,-X的补码。而在原码乘法中,是直接加上X
另外,ACC与MQ右移时,采用的是算数右移而不是原码的逻辑右移,这意味着如果当前ACC和MQ组成的补码表示一个负数,那么应该保持符号位不变,数值位右移并补1
这个过程需要重复5次,MQ中的符号位也参与运算
除法运算
恢复余数法
该方法针对原码除法
以0.1011 ÷ 0.1101为例
首先将MQ的最低位置1,即默认0.1011 ÷ 0.1101的第一位是1,用ACC减去X,即ACC加上-X的补码,得到11110,符号位为1,变成负数,也就是说X比ACC更大。此时说明MQ的最低位1是错误的,因此再把MQ的最低位置0,ACC再次加上X的补码,就恢复了原本的数
如果符号位为0,则说明置1是正确的,按照除法竖式错位相减的规则,只需要把ACC和MQ整体逻辑左移一位即可,右边空位补0
如此重复5次,在ACC中得到的数是余数,而MQ中的则是商
 https://blog.dearxuan.com/2022/05/04/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90%E5%8E%9F%E7%90%86-%E5%AE%9A%E7%82%B9%E6%95%B0%E8%BF%90%E7%AE%97/
https://blog.dearxuan.com/2022/05/04/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90%E5%8E%9F%E7%90%86-%E5%AE%9A%E7%82%B9%E6%95%B0%E8%BF%90%E7%AE%97/