摘要

Transformer注意力机制中的设计选择，包括弱归纳偏置和平方计算复杂度，限制了它在建模长序列中的应用。本文提出了Mega，一种简单且理论上有基础的单头门控注意力机制，该机制配备了（指数）移动平均，旨在将位置感知的局部依赖的归纳偏置引入到位置无关的注意力机制中。我们进一步提出了Mega的一个变种，该变种提供了线性时间和空间复杂度，但仅导致极小的质量损失，通过高效地将整个序列分成多个固定长度的块来实现。在一系列序列建模基准测试上，包括长程竞技场、神经机器翻译、自回归语言建模、图像和语音分类，广泛的实验表明，Mega在这些任务上相较于其他序列模型（包括Transformer的变种和近期的状态空间模型）取得了显著的提升。

1. 引言

设计一个统一的模型来捕捉顺序数据中的长程依赖关系，适用于多种不同的模态，如语言、音频、图像和视频，是序列建模中的一个核心且具有挑战性的问题。为此，已经开发了许多不同的架构，包括卷积神经网络（CNNs）（Kim, 2014; Strubell等, 2017）、循环神经网络（RNNs）（Goller和Kuchler, 1996; Hochreiter和Schmidhuber, 1997; Cho等, 2014）、Transformer（Vaswani等, 2017）以及最近的状态空间模型（SSMs）（Gu等, 2022a; Mehta等, 2022）。

在这些模型中，Transformer架构因其在广泛的语言和视觉任务上取得的显著经验性成功而脱颖而出，包括机器翻译（Vaswani等, 2017; Ott等, 2018）、语言理解（Devlin等, 2019; Liu等, 2019）、图像识别（Dosovitskiy等, 2020; Touvron等, 2021）和基因序列建模（Madani等, 2020; Jumper等, 2021），其主要得益于概念上吸引人的注意力机制（Bahdanau等, 2015; Luong等, 2015; Vaswani等, 2017），该机制直接建模输入标记之间的相互作用。

注意力机制提供了捕捉上下文信息的关键，它通过建模输入序列中每个时间步长的标记之间的成对交互来实现。然而，注意力机制的设计有两个常见缺点：i) 弱归纳偏置；ii) 平方计算复杂度。首先，注意力机制没有假设标记之间依赖关系的模式（例如位置归纳偏置），而是直接从数据中学习预测成对的注意力权重。其次，计算和存储注意力权重的成本是输入序列长度的平方。最近的研究已显示，在长序列任务中应用Transformer的局限性，既体现在准确性上，也体现在效率上（Tay等, 2020）。

在本研究中，我们提出了一种配备移动平均的门控注意力机制（Mega），旨在同时解决这两个问题。其关键思想是通过利用经典的指数移动平均（EMA）方法（Hunter, 1986），在时间步维度上将归纳偏置引入注意力机制。EMA捕捉了随着时间指数衰减的局部依赖关系（见图1），并广泛应用于时间序列数据建模（§2）。我们引入了一种具有可学习系数的多维衰减形式的EMA（§3.1），随后通过将EMA与单头门控注意力（Hua等, 2022）的变种结合，开发了配备移动平均的门控注意力机制（§3.2）。从理论上讲，我们证明了单头门控注意力与最常用的多头注意力具有相同的表达能力（§3.3）。得益于融入的移动平均机制，我们进一步提出了一个具有线性复杂度的Mega变种，称为Mega-chunk，它通过将输入序列简单地分成固定块来最小化上下文信息的损失（§3.5）。

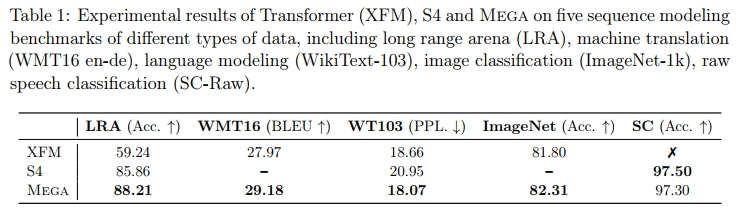
在实验中，通过在各种数据类型上的五个序列建模任务，包括长上下文序列建模、神经机器翻译、自回归语言建模、图像和语音分类，我们展示了Mega在有效性和效率上显著超过了多种强基准模型（§4）（见表1）。这些改进展示了通过不同归纳偏置模式建模长短期依赖关系的重要性。

2. 背景

在本节中，我们设置了符号表示，简要回顾了两种广泛使用的序列建模方法——自注意力机制和指数移动平均（EMA）——并讨论了将它们结合的动机。我们使用 $\mathbf{X}={\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_n\in {\mathbb{R}}^{n\times d}$ 来表示长度为 $n$ 的输入表示序列。令 $\mathbf{Y}={\mathbf{y}}_1,{\mathbf{y}}_2,\dots ,{\mathbf{y}}_n\in {\mathbb{R}}^{n\times d}$ 为每一层的输出表示序列，其长度与输入序列 $\mathbf{X}$ 相同，均为 $n$。在本文中，我们假设输入和输出序列的表示具有相同的维度 $d$。

2.1 自注意力机制

传统的自注意力机制是一个函数：

$$Y=Attn(X)=f(QKT\tau (X))VY=\mathrm{Attn}(X)=f\left(\frac{Q{K}^T}{\tau (X)}\right)V(1)$$

其中，Attn$:{\mathbb{R}}^n\times d\to {\mathbb{R}}^{n\times d}$ 是自注意力函数。$Q=X{W}_q+b_q,\mathbf{K}=\mathbf{X}{W}_k+b_k$ 和 $\mathbf{V}=\mathbf{X}{W}_v+b_v$ 是查询、键和值的序列，具有可学习的参数 $W_q,W_k,W_v\in {\mathbb{R}}^{d\times d}$，$b_q,b_k,b_v\in {\mathbb{R}}^d$。$f(\cdot )$ 是注意力函数，例如软最大函数 $f_{\text{softmax}}(\cdot )$（Bahdanau等, 2015），或最近提出的平方ReLU函数 $f_{{\mathrm{relu}}^2}(\cdot )$（So等, 2021；Hua等, 2022）。$\tau (\mathbf{X})$ 是一个缩放项，通常对于 $f_{\text{softmax}}(\cdot )$ 设置为 $\tau (\mathbf{X})=\sqrt{d}$，对于 $f_{\mathrm{rel}{\mathrm{u}}^2}(\cdot )$ 设置为 $\tau (\mathbf{X})=n$。常用的多头注意力变体将注意力函数并行执行 $h$ 次。

我们可以根据公式（1）定义一个矩阵 $\mathbf{A}=f\left(\frac{Q{\mathbf{K}}^T}{\tau (\mathbf{X})}\right)\in {\mathbb{R}}^{n\times n}$，该矩阵称为注意力矩阵，表示了输入序列中每一对标记之间的依赖关系强度。由于它建模了成对的依赖关系权重，因此 $\mathbf{A}$ 矩阵原则上提供了一个灵活且强大的机制，能够学习长距离的依赖关系，并具有最小的归纳偏置。然而，实际上，直接从数据中识别所有依赖关系模式是一个具有挑战性的任务，尤其是在处理长序列时。此外，使用 $h$ 个注意力头计算 $\mathbf{A}$ 的时间和空间复杂度为 $O(h{n}^2)$，而序列长度的平方依赖关系成为一个显著的瓶颈。

2.2 指数移动平均（EMA）

移动平均是一种经典的序列数据建模方法，广泛用于时间序列数据中，以平滑短期波动并突出长期趋势或周期。指数移动平均（EMA）（Winters, 1960；Hunter, 1986）是移动平均的一个特例，应用递减的权重因子。形式上，EMA递归地计算输出序列 $Y$：
$$yt=\alpha \odot xt+(1-\alpha )\odot yt-1y_t=\alpha \odot x_t+(1-\alpha )\odot y_{t-1}\text{\hspace{1em}(2)}$$
其中，$\alpha \in (0,1{)}^d$ 是EMA系数，表示权重衰减的程度，$\odot$ 是元素逐项相乘。较高的 $\alpha$ 会更快地降低旧观测值的权重（见图1）。

使用EMA在学习成对依赖关系时施加了强烈的归纳偏置：两个标记之间的依赖权重随着时间的推移以输入无关的衰减因子 $\alpha$ 指数下降。这个属性有利于局部依赖，并限制了长距离依赖。尽管在公式（2）中采用了递归的形式，EMA的计算可以表示为 $n$ 个独立的卷积运算，可以通过快速傅里叶变换（FFT）高效地计算（详细信息请见附录A）。

2.3 为什么将注意力机制与EMA结合？

如第2.1节和第2.2节所述，尽管EMA和注意力机制在序列建模中有广泛的应用并取得了显著成功，但它们各自也有其局限性。通过利用它们各自的特点以互相补充，我们提出将EMA嵌入到注意力矩阵A的计算中。由此得到的模型既能享受强归纳偏置的优势，又能保持学习复杂依赖模式的能力。此外，这种集成方法使得我们可以设计出一种计算上高效的分块注意力机制，相对于序列长度具有线性复杂度（§3.5）。

3. 移动平均驱动的门控注意力（Mega）

在本节中，我们详细介绍我们提出的方法——移动平均驱动的门控注意力（Mega）。首先，我们介绍多维衰减EMA（§3.1），它是与Mega中的单头门控注意力结合的关键组件（§3.2），并讨论Mega与三个密切相关的模型：GRU（Cho et al., 2014）、Flash（Hua et al., 2022）和S4（Gu et al., 2022a）之间的关系。我们还为单头门控注意力的设计提供理论依据（§3.3）。接着，我们描述每个Mega模块的详细架构，包括前馈层和归一化层（§3.4）。最后，我们介绍Mega-chunk，它是Mega的一个变体，简单地将输入序列分割成固定的块，从而将时间和空间复杂度从二次复杂度降低到线性复杂度（§3.5）。

3.1 多维衰减EMA

MEGA引入了标准EMA的修改版，称为多维衰减EMA，以提高其灵活性和能力。

衰减EMA。以往的研究（McKenzie和Gardner Jr，2010；Svetunkov，2016）表明，通过放宽先前和当前观测值的耦合权重（公式（2）中的$\mathbf{\alpha }$与$1-\mathbf{\alpha }$）可以生成更加稳健的依赖建模。受到此启发，MEGA允许对前一个时间步的影响进行衰减：
$$yt=\alpha \odot xt+(1-\alpha \odot \delta )\odot yt-1,\mathbf{y}t=\alpha \odot \mathbf{x}t+(1-\alpha \odot \delta )\odot {\mathbf{y}}_{t-1}\text{\hspace{1em}(3)}$$
其中，$\delta \in (0,1{)}^d$ 是衰减因子。

多维衰减EMA。为了进一步提高EMA的表达能力，我们引入了EMA的多维变体。具体来说，我们首先通过扩展矩阵$\beta \in {\mathbb{R}}^{d\times h}$将输入序列$\mathbf{X}$的每个维度单独扩展为$h$个维度。形式上，对于每个维度$j\in 1,2,\dots ,d$，我们有：
$$ut(j)={\beta }_j{x}_{t,j}\text{\hspace{1em}(4)}$$
其中，${\beta }_j\in {\mathbb{R}}^h$是$\beta$的第$j$行，${\mathbf{u}}_t^{(j)}\in {\mathbb{R}}^h$是时间步$t$下第$j$维度的扩展后的$h$维向量。

相应地，我们将$\mathbf{\alpha }$和$\mathbf{\delta }$的形状从一维向量扩展为二维矩阵，即$\mathbf{\alpha },\mathbf{\delta }\in {\mathbb{R}}^{d\times h}$，其中${\mathbf{\alpha }}_j,{\mathbf{\delta }}_j\in {\mathbb{R}}^h$分别表示$\mathbf{\alpha }$和$\mathbf{\delta }$的第$j$行。然后，对于每个维度$j$，将衰减EMA应用于$h$维隐藏空间：
$$h_t(j)={\alpha }_j\odot u_t^j+(1-{\alpha }_j\odot {\delta }_j)\odot h_{t-1}^j$$

$${\mathbf{y}}_{t,j}={\eta }_j^T{\mathbf{h}}_t^{(j)}\text{\hspace{1em}(5)}$$

其中，${\mathbf{h}}_t^{(j)}\in {\mathbb{R}}^h$是时间步$t$下第$j$维度的EMA隐藏状态，$\mathbf{\eta }\in {\mathbb{R}}^{d\times h}$是一个投影矩阵，用于将$h$维隐藏状态映射回1维输出${\mathbf{y}}_{t,j}\in \mathbb{R}$。${\mathbf{\eta }}_j\in {\mathbb{R}}^h$是$\mathbf{\eta }$的第$j$行。由(5)得到的输出$\mathbf{Y}$表示为$\mathbf{Y}\stackrel{\Delta }{=}$ EMA$(\mathbf{X})$。因为我们不需要显式地计算$\mathbf{h}{t}^{(j)}$来得到输出${\mathbf{y}}_{t,j}$，所以时间和空间复杂度与标准EMA（公式（2））相似（详细内容见附录A）。实验结果表明，它的效果得到了提升（§4）。

3.2 移动平均装备门控注意力

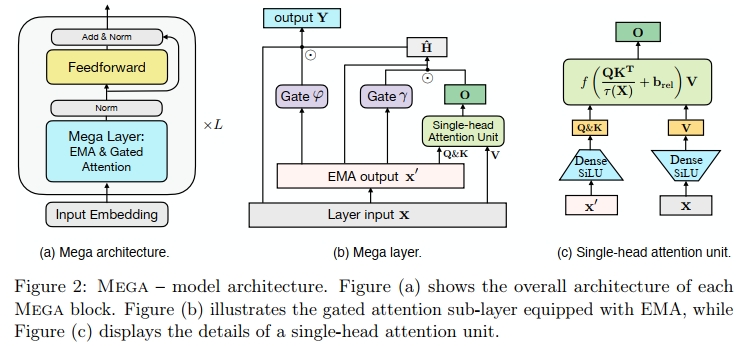
Mega中的门控注意力机制采用了门控递归单元（GRU; Cho等人，2014）和门控注意力单元（GAU; Hua等人，2022）作为骨干架构，并将基于EMA的子层嵌入到注意力矩阵的计算中。形式上，我们首先使用(5)中的输出计算GAU中的共享表示：
$$\begin{array}{rlrlrl}& X^{\prime }=\mathrm{EMA}(X)& & \in {\mathbb{R}}^{n\times d}& & (6)\\ & \mathbf{Z}={\varphi }_{\mathrm{silu}}({\mathbf{X}}^{\prime }{W}_z+b_z)& & \in {\mathbb{R}}^{n\times z}& & (7)\end{array}$$
其中，$X^{\prime }$ 可以视为更新后的或上下文化的输入，因为它通过EMA编码了上下文信息。$Z$ 是共享表示，具有 $z$ 维度，投影矩阵为 $W_z\in {\mathbb{R}}^{d\times z}$，偏置项为 $b_z\in {\mathbb{R}}^z$。${\varphi }_{silu}$ 是自门控激活函数（SiLU）（Ramachandran等人，2017；Elfving等人，2018）。继GAU之后，查询和键序列通过对$Z$应用每维标量和偏移量来计算，而值序列则来自原始的$X$：
$$\begin{array}{c}\mathrm{C}!={\kappa }_q\odot Z+{\mu }_q\in {\mathbb{R}}^{n\times z}\left(8\right)\\ \mathrm{K}={\kappa }_k\odot Z+{\mu }_k\in {\mathbb{R}}^{n\times z}(9)\\ \mathrm{V}={\varphi }_{\mathrm{silu}}(X{W}_v+b_v)\in {\mathbb{R}}^{n\times v}(10)\end{array}$$
其中，${\kappa }_q,{\mu }_q,{\kappa }_k,{\mu }_k\in {\mathbb{R}}^2$ 是查询和键的可学习标量和偏移量。$v$ 是值序列的扩展中间维度。注意力的输出计算如下：
$$O=f\left(\frac{Q{K}^T}{\tau (X)}+b_{\mathrm{rel}}\right)V\in {\mathbb{R}}^{n\times v}\text{\hspace{1em}(11)}$$
图形规范显示在图 2 © 中。$b_{rel}\in {\mathbb{R}}^{n\times n}$ 是相对位置偏差。我们选择$b_{rel}$来自现有的方法，包括T5（Raffel 等人，2020），RoPE（Sutton 等人，2021），TUPE（Ke 等人，2020）和ALiBi（Press 等人，2021）。随后，MEGA 引入了重置门 $\gamma$、更新门 $\phi$，并计算候选激活输出 $\hat{H}$：
$$\gamma ={\varphi }_{\mathrm{silu}}({\mathbf{X}}^{\prime }{W}_{\gamma }+b_{\gamma })\in {\mathbb{R}}^{n\times v}\text{\hspace{1em}(12)}$$

$$\phi ={\varphi }_{\mathrm{sigmoid}}({\mathbf{X}}^{\prime }{W}_{\phi }+b_{\phi })\in {\mathbb{R}}^{n\times d}\text{\hspace{1em}(13)}$$

$$\hat{\mathbf{H}}={\varphi }_{\mathrm{silu}}({\mathbf{X}}^{\prime }{W}_h+(\gamma \odot \mathbf{O})U_h+b_h)\in {\mathbb{R}}^{n\times d}\text{\hspace{1em}(14)}$$

最终输出 $Y$ 是通过更新门 $\phi$ 计算得到的：
$$Y=\phi \odot \hat{H}+(1-\phi )\odot X\in {\mathbb{R}}^{n\times d}\text{\hspace{1em}(15)}$$
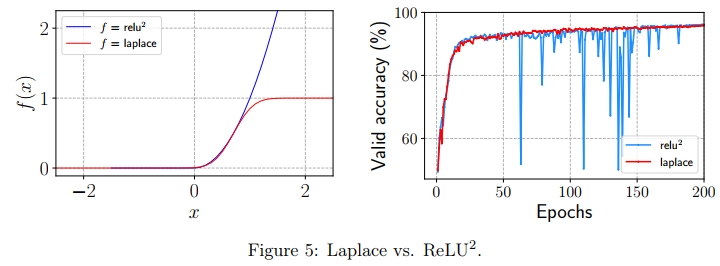
Mega子层的图形架构如图2(b)所示。拉普拉斯注意力函数。如第2.1节所述，softmax函数是最常见的注意力函数f(·)。So等人（2021）最近通过架构搜索技术引入了平方ReLU函数frelu2(·)，该函数在语言任务上表现出更快的收敛速度和具有竞争力的泛化性能（Hua等人，2022）。然而，frelu2(·)的一个问题是其范围和梯度都没有界限，导致模型训练不稳定（有关详细信息，请参见附录C.1）。为了应对这个问题，我们提出了一种基于拉普拉斯函数的新注意力函数。
$$f_{\text{lplace}}(x;\mu ,\sigma )=0.5\times [1+\text{erf}\left(\frac{x-\mu }{\sigma \sqrt{2}}\right)]\text{\hspace{1em}(16)}$$
其中，erf() 是误差函数。μ 和 σ 是我们调整的两个系数，用来逼近 $f_{rel{u}^2}$，从而得到 $\mu =\sqrt{1/2}$ 和 $\sigma =\sqrt{1/4\pi }$。拉普拉斯函数的推导和可视化请参见附录C。

与GRU、Flash和S4的关系与区别。重置门γ、更新门’以及候选激活输出H^的计算（公式12-14）让人联想到GRU（Cho等人，2014）。主要区别在于，在GRU中，两个门是应用于当前和前一个时间步的隐藏状态之间，而在Mega中，它们是应用于EMA和门控注意力子层的输出之间。此外，公式（15）中的输出门控机制类似于Parisotto等人（2020）和Xu等人（2020）提出的门控残差连接，用以减少输出Y的方差。

共享表示Z的计算，以及公式（7-10）中查询、键和值的序列，受到Flash中GAU的启发（Hua等人，2022）。Mega通过从EMA输出X0而不是原始输入X计算公式（7）中的Z，将EMA整合到GAU中，并将GAU输出与X0结合用于公式（14）中的候选激活H^。与Flash相比的实验结果表明了这一设计选择的有效性（第4.1节）。

多维衰减EMA可以看作是状态空间模型的简化变种。从这个角度来看，Mega与S4（Gu等人，2022a）也有紧密的关系，后者是一个具有结构化状态矩阵的状态空间模型。S4利用HiPPO框架（Gu等人，2020）来初始化其低秩结构化状态矩阵，而S4中卷积核的计算需要复杂的快速傅里叶变换（FFT）。Mega中的EMA子层对状态矩阵进行了对角化，并将对角元素限制在（0，1）范围内。因此，卷积核将是一个范德蒙德积，可以以高效且数值稳定的方式进行计算。类似的对角化在并行工作S4D（Gu等人，2022b）中也有使用。此外，不像S4和S4D，Mega中的参数初始化不依赖于HiPPO框架。

3.3 单头门控注意力的理论依据

实验证明，单头门控注意力在性能上与普通的多头注意力相当（Liu等人，2021；Hua等人，2022），但对其理论见解并未进行讨论。在这一节中，我们提供了单头门控注意力表达能力的理论依据。为了便于后续分析，我们简化了多头注意力的符号表示。具体来说，我们将查询、键和值的序列表示为输入序列的三种变换的输出：
$$Q=\mathcal{Q}(X),K=\mathcal{K}(X),V=\mathcal{V}(X)\text{\hspace{1em}(17)}$$
其中，$\mathcal{Q},\mathcal{K},\mathcal{V}$ 是三个变换，例如线性投影。设 $\mathbf{q}\in \mathbf{Q}={\mathbf{q}}_1,\dots ,{\mathbf{q}}_n$ 是一个单一的查询向量（$\mathbf{q}\in {\mathbb{R}}^d$），并且 $\mathbf{a}=\mathcal{A}(\mathbf{q},\mathbf{K})$ 表示 $\mathbf{q}$ 对应的注意力权重，其中 $\mathcal{A}$ 是注意力变换，即公式（11）中的 $f(\cdot )$。

对于多头注意力，一个常见的实现方法是将查询向量拆分成 $h$ 个头，在模型维度上进行分割：
$$\mathbf{q}=\left[\begin{array}{c}{\mathbf{q}}^{(1)}\\ ⋮\\ {\mathbf{q}}^{(h)}\end{array}\right]\text{\hspace{1em}(18)}$$
其中，${\mathbf{q}}^{(i)}\in {\mathbb{R}}^{d/h}$，且 $i\in 1,\dots ,h$ 是第 $i$ 个头的查询向量。$\mathbf{K}$ 和 $\mathbf{V}$ 也按相同方式进行分割。第 $i$ 个头的注意力权重为 $a^{(i)}=\mathcal{A}({\mathbf{q}}^{(i)},{\mathbf{K}}^{(i)})$。然后，单头和多头注意力的输出分别为：
$$O_{\mathrm{SHA}}={\mathbf{a}}^T\mathbf{V}=\left[\begin{array}{c}{\mathbf{a}}^T{\mathbf{V}}^{(1)}\\ ⋮\\ {\mathbf{a}}^T{\mathbf{V}}^{(h)}\end{array}\right],{\mathbf{O}}_{\mathrm{MHA}}=\left[\begin{array}{c}{\mathbf{a}}^{(1{)}^T}{\mathbf{V}}^{(1)}\\ ⋮\\ {\mathbf{a}}^{(h{)}^T}{\mathbf{V}}^{(h)}\end{array}\right]\text{\hspace{1em}(19)}$$
很容易看出，$O_{\mathrm{MHA}}$ 比 $O_{\mathrm{SHA}}$ 更具表达能力，因为 $O_{\mathrm{MHA}}$ 利用了 $h$ 组注意力权重。

在单头门控注意力中，我们为每个 $\mathbf{q}$ 引入一个门控向量 $\gamma =\mathcal{G}(\mathbf{X})$，单头门控注意力的输出为 $O_{\mathrm{SHGA}}=O_{\mathrm{SHA}}\odot \gamma$。以下定理揭示了 $O_{\mathrm{SHGA}}$ 和 $O_{\mathrm{MHA}}$ 在表达能力上的等价性（证明见附录B）：

定理 1 假设变换 $\mathcal{G}$ 是一个 $a$ 型的普适逼近器。那么，对于每个 $\mathbf{X}$，存在一个 $\mathbf{\gamma }=\mathcal{G}(\mathbf{X})$，使得
$$O_{\mathrm{SHGA}}=O_{\mathrm{MHA}}\text{\hspace{1em}(20)}$$
定理 1 表明，通过简单地引入门控向量，$O_{\mathrm{SHGA}}$ 与 $O_{\mathrm{MHA}}$ 在表达能力上是等价的。实际上，变换 $\mathcal{G}$ 通常通过一个（浅层）神经网络来建模，其逼近的普适性已经得到广泛研究（Hornik等人，1989；Yarotsky，2017；Park等人，2020）。

3.4 Mega块

Mega层（带有移动平均的门控注意力）可作为Transformer中常规注意力的替代层。它后面跟随逐位置的前馈网络（FFNs）和归一化层，组成一个Mega块。由于门控残差连接已经包含在公式（15）中，我们省略了原始的残差连接，直接对 $Y$ 应用归一化层：具体而言，
$$\begin{array}{rl}& \mathbf{Y}=\mathrm{Norm}(\mathrm{Mega}(\mathbf{X}))\\ & {\mathbf{Y}}^{\prime }=\mathrm{Norm}(\mathrm{FFN}(\mathbf{Y})+\mathbf{Y})\end{array}\text{\hspace{1em}(21)}$$
在这里，Y₀ 是 Mega block 的输出。Mega block 的整体架构如图 2 (a) 所示。在 Transformer 中，FFN（前馈网络）的隐藏维度通常设置为 $d_{FFN}=4d$。为了保持与每个 Transformer block 相似的模型规模，我们将 FFN 的隐藏维度减小为$ d_{FFN }= 2d$，并将公式（10）中值序列的扩展维度 v 设置为 2d，除非另有说明。

3.5 Mega-chunk：具有线性复杂度的 Mega

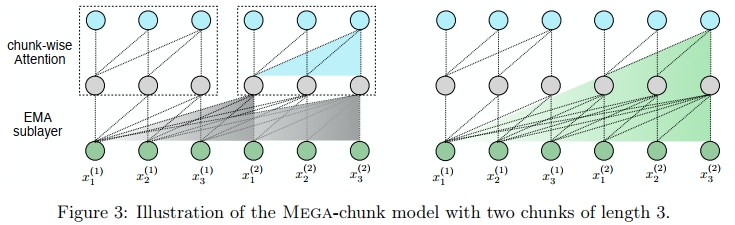
到目前为止，我们只关注在注意力机制中引入更强的归纳偏差，而注意力机制本身仍然具有平方的计算复杂度。在本节中，我们提出了 Mega-chunk，Mega 的一个变种，具有线性复杂度，它通过将注意力应用于每个固定长度的局部块来简化计算。

具体来说，我们首先将（8-10）式中的查询、键和值序列划分为长度为 $c$ 的块。例如，$Q=Q_1,\dots ,Q_k$，其中 $k=n/c$ 是块的数量。注意力操作（11）分别应用于每个块，从而使计算复杂度为 $O(k{c}^2)=O(nc)$，相对于 $n$。然而，这种方法存在一个关键的限制，即它会丧失来自其他块的上下文信息。幸运的是，MEGA 中的 EMA 子层通过捕捉每个 token 附近的局部上下文信息来缓解这一问题，这些输出被用作注意力子层的输入。因此，块级注意力所利用的有效上下文可以超越块边界。图 3 展示了一个 MEGA-chunk 块所能捕捉到的最大依赖长度。

4. 实验

为了评估 Mega，我们在五个基准序列建模任务上进行了实验，涵盖了各种数据类型，并与当前在每个任务上的最先进模型进行了比较。所有带有 z 的数字表示我们复现的基准模型的结果。更详细的描述、结果和分析见附录 D。

4.1 长上下文序列建模

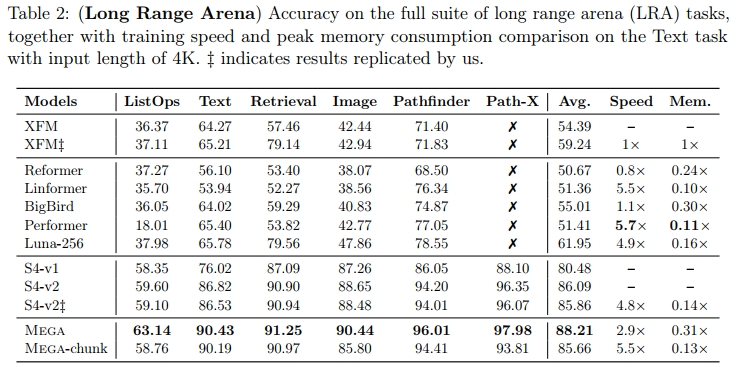
我们从在最近由 Tay 等人（2021）提出的长范围竞技场（LRA）基准上的评估开始，这个基准旨在评估长上下文场景下的序列模型。他们在这个基准中收集了六个任务，分别是 ListOps（Nangia 和 Bowman, 2018）、字节级文本分类（Text；Maas 等人, 2011）、字节级文档检索（Retrieval；Radev 等人, 2013）、基于像素序列的图像分类（Image；Krizhevsky 等人, 2009）、Pathfinder（Linsley 等人, 2018）及其极长版本（Path-X；Tay 等人, 2021）。这些任务包括了从 1K 到 16K token 的输入序列，涵盖了多种数据类型和模态。

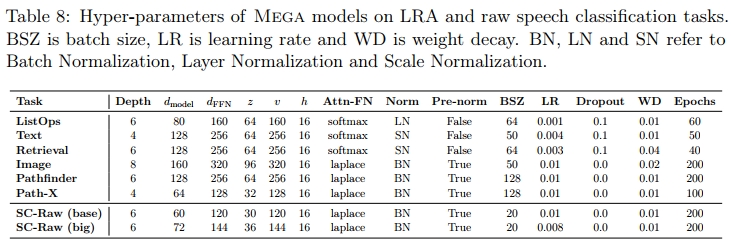
表 2 比较了 Mega 与几个基准模型的表现，包括 Transformer 及其高效变体，以及最先进的 S4 模型（包括版本 1（Gu 等人，2022a）和版本 2（Gu 等人，2022b））。为了确保公平比较，我们在每个任务上调整了层数和模型维度，使得 Mega 的参数数量与 S4-v1 相似。对于每个实验，我们报告了 5 次不同随机种子的平均结果。调优信息和模型细节见附录 D.1。

在所有六个任务中，Mega 明显优于所有基准模型。我们还在每个任务上评估了 Mega-chunk，通过将所有任务的块大小设为 c = 128，除了 Path-X，其中 c = 4096。我们观察到 Mega-chunk 始终表现良好，尤其在三个语言任务上表现突出。我们还检查了 Mega 在字节级分类任务（输入长度为 4K）上的速度和内存效率。Mega-chunk 的效率非常高，速度是普通 Transformer 的 5.5 倍，内存消耗仅为 Transformer 的 13%。有趣的是，具有完整注意力域的 Mega 在效率上也明显优于 Transformer，得益于单头门控注意力。

多维阻尼 EMA 的分析
为了展示 Mega 中多维阻尼 EMA 组件的有效性，我们对两个 LRA 任务（字节级文本分类（Text）和像素序列图像分类（Image））进行了消融实验。我们训练了具有不同 EMA 维度 $h ∈ {0, 1, 2, 4, 8, 16, 32} $的 Mega 模型，其中 h = 0 表示移除 EMA 组件。从图 4 左侧的图像中，我们可以看到，在没有 EMA 组件的情况下，两个任务的模型准确率迅速下降。同时，通过使用一维 EMA（h = 1），Mega 在两个任务上都获得了显著提升，证明了通过 EMA 引入归纳偏差的重要性。

块大小的分析
我们进一步分析了块大小 c 对同两个任务的影响，通过改变 c ∈ {16, 32, 64, 128, 256, 512, 1}，其中 1 表示原始的没有分块的 Mega。图 4 右侧的图像显示，图像数据对块大小比文本数据更敏感。在 Text 任务中，即使是小块大小 c = 16 的 Mega-chunk 也能达到约 90% 的准确率。在 Image 任务中，Mega-chunk 使用 c = 16 取得了约 75% 的准确率，这仍然远超普通 Transformer 模型。

注意力函数的分析
最后，我们评估了不同注意力函数的性能。表 3 显示了三种注意力函数在相同两个任务上的准确率。在文本数据上，softmax 获得了最佳准确率，而在图像数据上表现最差。laplace 函数在图像数据上获得了最佳准确率，并且在文本数据上也表现得相当有竞争力，始终优于 $rel{u}^2$。在以下实验中，我们对语言任务使用 softmax，对视觉和语音任务使用 laplace。

4.2 原始语音分类

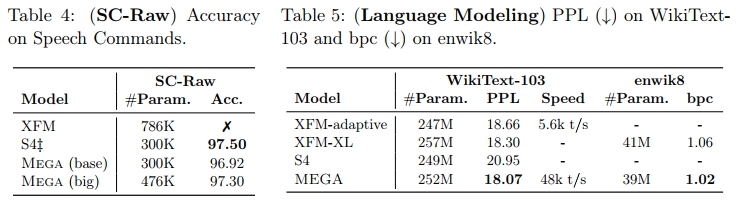
为了评估 Mega 在长范围建模语音信号方面的能力，我们将 Mega 应用于原始语音分类（长度为 16000），而不是使用传统的预处理方法（例如转换为 MFCC 特征）。按照 Gu 等人（2022a）的方法，我们在 Speech Commands 数据集的 SC10 子集上进行语音分类（Warden，2018）。我们使用 Mega-chunk 变体，块大小设为 c = 1000，因为 Mega 和 Transformer 的计算无法适应 GPU 内存。如表 4 所示，我们的 Mega-chunk（base）模型，具有 30 万个参数，能够达到 96.92 的准确率，略低于最先进的 S4 方法的 97.50。然而，通过增加 0.18M 参数，Mega-chunk（big）模型的表现与 S4 相当。

4.3 自回归语言建模

我们在两个已建立的语言建模基准上评估 Mega——WikiText-103（Merity 等人，2017）和 enwik8（Hutter，2006），这两个任务都是预测下一个 token。WikiText-103 是一个词级别的语言建模数据集，包含来自 Wikipedia 文章的 1.03 亿个训练 token。根据之前的工作（Baevski 和 Auli，2018；Dai 等人，2019），我们采用了自适应 softmax 和输入嵌入，并使用 26 万词汇表。Enwik8 是一个字符级别的语言建模基准，包含来自未处理的 Wikipedia 文章的 1 亿个 token，词汇表大小约为 200。在测试时，我们将测试数据分割成多个段，并按顺序处理每个段。在表 5 中，我们与之前的顶级模型进行了比较，

这些模型旨在利用更长的上下文，包括 Transformers（Baevski 和 Auli，2018；Al-Rfou 等人，2019）（XFM-adaptive），Transformer-XL（Dai 等人，2019）（XFM-XL）和 S4（Gu 等人，2022a）。在 WikiText-103 和 enwik8 上，我们获得了非常具有竞争力的结果，显著超越了基准模型，同时相比 Transformer 模型享有更快（9 倍）的推理速度。由于 EMA 层的递归设计，Mega 在推理时也能自然地实现长度外推，适应比训练时更长的序列。此外，由于在训练中使用了旋转位置嵌入（Su 等人，2021），我们还可以对 Mega 的注意力块大小进行外推。我们在附录 D.3 中详细描述了这些内容，并提供了使用不同测试时块大小和段长度的完整结果。

4.4 神经机器翻译

为了评估 Mega 在序列到序列建模上的表现，我们在一个标准的机器翻译基准上进行了实验，即 WMT 2016 英语-德语新闻翻译（WMT’16），该数据集包含 450 万句对的训练数据。按照 Ott 等人（2018）的方法，我们在 newstest13 上进行验证，并在 newstest14 上进行测试。Mega 模型的架构紧跟 Transformer-base：6 个编码器和解码器层，模型维度 d = 512。

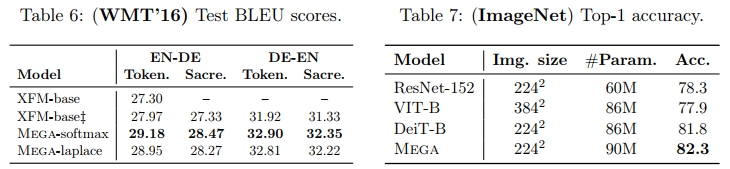
表 6 展示了 WMT’16 测试集的 BLEU 分数，包括两个方向：EN→DE 和 DE→EN。对于每个实验，我们报告了 5 个不同随机种子的平均结果，包括标记化的 BLEU 分数和 SacreBLEU（Post，2018）分数。Mega-base 明显优于 Transformer-base，BLEU 分数提高了超过 1.1。我们还报告了使用 Laplace 注意力函数的 Mega 的结果，尽管它略微但持续地逊色于 Softmax。

4.5 图像分类

为了评估 Mega 在大规模图像分类任务上的表现，我们在 Imagenet-1k（Deng 等人，2009）数据集上进行了实验，该数据集包含 128 万张训练图像和 5 万张验证图像，来自 1000 个类别。表 7 中报告了在验证集上的 Top-1 准确率，以评估不同模型的表现。Mega 相较于 DeiT-B（Touvron 等人，2021）获得了大约 0.5% 的准确率提升。我们大部分遵循 DeiT 的方法，应用了多种数据增强和正则化方法来促进训练过程，包括 Cutmix（Yun 等人，2019）、Mixup（Zhang 等人，2017）、随机深度（Huang 等人，2016）、重复增强（Hoffer 等人，2020）、Rand-Augment（Cubuk 等人，2020）和随机擦除（Zhong 等人，2020）。这些方法主要针对优化 DeiT 的性能进行了高度调优，可能对于 Mega 来说并不是最优的。探索适合 Mega 的最佳数据增强和正则化方法是未来工作的一个有趣方向。更多的训练细节见附录 D.5。

5. 相关工作

最近有许多技术被提出，以解决 Transformer 模型的两个问题；由于篇幅限制，这里仅提到其中的一些。

归纳偏差
为了将更强的归纳偏差引入注意力机制，一个研究方向集中于通过高级位置编码方法注入位置信息，包括绝对和相对位置嵌入（Vaswani 等人，2017；Huang 等人，2020；Ke 等人，2020），以及相对位置偏置（Su 等人，2021；Press 等人，2021）。另一个研究方向将注意力机制与其他具有内在强归纳偏差的神经架构相结合，如卷积（Gehring 等人，2017；Dai 等人，2021）和递归（Dai 等人，2019；Rae 等人，2020；Lei，2021）。

计算效率
最近出现了许多先进的 Transformer 模型变体（“xformers”）（Tay 等人，2020，2021），旨在提高时间和内存效率。流行的技术包括稀疏注意力模式（Parmar 等人，2018；Beltagy 等人，2020；Kitaev 等人，2020），注意力矩阵的低秩近似（Wang 等人，2020；Ma 等人，2021），以及通过核化近似（Choromanski 等人，2020；Peng 等人，2021）。尽管这些模型在长序列上展示了更好的渐进复杂度，但它们在中等长度序列上的效率提升不明显，其性能仍落后于常规注意力的 Transformer 模型。

具有连续核的卷积神经网络
由于 EMA 及更一般的状态空间模型（如 S4）可以视为序列长度等于核大小的卷积变换，Mega 也与具有连续核的 CNN（卷积神经网络）相关，包括 CKConv（Romero 等人，2021）、FlexConv（Romero 等人，2022a）和 CCNN（Romero 等人，2022b）。

6. 结论

我们介绍了 Mega，这是一种简单、高效且有效的神经架构，可作为常规多头注意力的替代方案。通过利用经典的指数移动平均（EMA）方法，Mega 能够将更强的归纳偏差融入注意力机制。此外，EMA 方法还使得 Mega-chunk 的设计成为可能，Mega-chunk 是 Mega 的一个高效变种，具有线性复杂度。在五个涉及各种数据类型的序列建模任务中，Mega 显著超越了包括之前的最先进系统在内的多种强基准模型。这些改进为未来将 Mega 应用于多模态建模提供了潜在方向。

附录：Mega：带有移动平均门控注意力的模型

附录 A. 多维阻尼 EMA 的高效计算

注意，不同维度的多维阻尼 EMA 计算彼此完全独立。在不失一般性的情况下，我们设定 d = 1，并在以下公式中省略维度索引 j。我们将初始隐藏状态表示为 h0h_0。在（5）中定义的多维阻尼 EMA 可以向量化为以下公式：
$${\mathbf{h}}_t=\alpha \odot {\mathbf{u}}_t+(1-\alpha \odot \delta )\odot {\mathbf{h}}_{t-1}\text{\hspace{1em}(22)}$$

$${\mathbf{y}}_t={\eta }^T{\mathbf{h}}_t\text{\hspace{1em}(23)}$$

其中 α、δ 和 $\eta \in R^h$，$u_t=\beta x_t\in R^h$，$h_t\in R^h$ 是时刻 t 的 EMA 隐藏状态。我们设 $\phi =1-\alpha \odot \delta$。然后，明确展开上述两个方程得到：

${\mathbf{h}}_1=\varphi \odot {\mathbf{h}}_0+\alpha \odot \beta {\mathbf{x}}_1$ ${\mathbf{h}}_2={\varphi }^2\odot {\mathbf{h}}_0+\varphi \odot \alpha \odot \beta {\mathbf{x}}_1+\alpha \odot \beta {\mathbf{x}}_2$

${\mathbf{y}}_1={\eta }^T\varphi \odot {\mathbf{h}}_0+{\eta }^T\alpha \odot \beta {\mathbf{x}}_1$ ${\mathbf{y}}_2={\mathbf{\eta }}^T{\mathbf{\varphi }}^2\odot {\mathbf{h}}_0+{\mathbf{\eta }}^T\mathbf{\varphi }\odot \mathbf{\alpha }\odot \mathbf{\beta }{\mathbf{x}}_1+{\mathbf{\eta }}^T\mathbf{\alpha }\odot \mathbf{\beta }{\mathbf{x}}_2$

这可以写成一个向量化的公式：
$$\mathbf{y}t={\eta }^T{\varphi }^t\odot \mathbf{h}0+{\eta }^T{\varphi }^{t-1}\odot \alpha \odot \beta \mathbf{x}1+\dots +{\eta }^T\alpha \odot \beta \mathbf{x}t\text{\hspace{1em}(24)}$$

$$\mathbf{y}=\mathcal{K}\ast \mathbf{x}+{\eta }^T{\varphi }^t\odot {\mathbf{h}}_0\text{\hspace{1em}(25)}$$

其中 * 是具有核 $K ∈ ℝ^n $的卷积变换：
$$\mathcal{K}=\left(\begin{array}{cccc}{\eta }^T(\alpha \odot \beta ),& {\eta }^T(\varphi \odot \alpha \odot \beta ),& \dots ,& {\eta }^T({\varphi }^t\odot \alpha \odot \beta )\end{array}\right)\text{\hspace{1em}(26)}$$
在提出的多维阻尼 EMA 中，K 可以通过 Vandermonde 乘积高效计算。给定 K 后，可以通过 FFT 高效计算公式 (25) 中的输出 y。

附录 B. 定理 1 的证明

证明：我们将 γ 分成 h 个头，方式与 Q、K 和 V 相同：
$$\gamma =\left[\begin{array}{c}{\gamma }^{(1)}\\ ⋮\\ {\gamma }^{(h)}\end{array}\right]$$
然后我们得到：
$$O_{\mathrm{SHGA}}=a^{T}V\odot \gamma =\left[\begin{array}{c}{a}^T{V}^{(1)}\odot {\gamma }^{(1)}\\ ⋮\\ a^T{V}^{(h)}\odot {\gamma }^{(h)}\end{array}\right]$$
为了证明定理 1，我们需要找到 γ，使得：
a T V ( i ) ⊙ γ ( i ) = a ( i ) T V ( i ) ⟺ γ ( i ) = a ( i ) T V ( i ) ⊘ a T V ( i ) , ∀ i ∈ { 1 , … , h } a^T\boldsymbol{V}^{(i)}\odot\boldsymbol{\gamma}^{(i)}=\boldsymbol{a}^{(i)^T}\boldsymbol{V}^{(i)}\Longleftrightarrow\boldsymbol{\gamma}^{(i)}=\boldsymbol{a}^{(i)^T}\boldsymbol{V}^{(i)}\oslash\boldsymbol{a}^T\boldsymbol{V}^{(i)},\forall i\in\{1,\ldots,h\} aTV(i)⊙γ(i)=a(i)TV(i)⟺γ(i)=a(i)TV(i)⊘aTV(i),∀i∈{1,…,h}
其中 ∅ 是逐元素除法操作。由于 G(X) 是一个通用逼近器，并且 Q、K、V 和 $a$ 都是从 X 转换而来，理论上 γ 可以恢复 $a^{(i)}$^TV(i)∅$a^T{V}^{(i)},\forall X$。

附录 C. 拉普拉斯注意力函数

为了使用（16）中的拉普拉斯函数近似平方 ReLU 函数，我们需要选择合适的系数 μ 和 σ。我们通过在$x=\sqrt{2}$ 时解以下两个方程来推导 μ 和 σ 的值：
$$f_{\mathrm{relu}2}(\sqrt{2})=f_{\mathrm{laplace}}(\sqrt{2})\text{\hspace{1em}(27)}$$

$$f_{\mathrm{relu}2}^{\prime }(\sqrt{2})=f_{\mathrm{laplace}}^{\prime }(\sqrt{2})\text{\hspace{1em}(28)}$$

公式（27）得出 $\mu =\sqrt{1/2}$，随后公式（28）给出 $\sigma =\sqrt{1/4\pi }$。图5展示了这两个函数的可视化结果。

C.1 稳定性：拉普拉斯 vs. 平方ReLU

除了性能改进之外，我们还研究了两种注意力函数的稳定性。我们在LRA Pathfinder任务上使用MEGA模型对这两种函数进行了实验。图5展示了训练过程中验证集上的准确率。我们观察到，拉普拉斯函数比ReLU${}^2$函数稳定得多。

附录 D. 实验细节

D.1 长距离竞技场（LRA）

对于所有任务，我们严格遵循 Tay 等人（2020）的工作，包括数据预处理、数据划分等细节。Mega 模型在这些任务上的超参数列于表 8 中。

D.2 原始语音分类

按照 Gu 等人（2022a）的研究，我们在 Speech Commands 数据集（Warden, 2018）的 SC10 子集上进行语音分类任务，这是一个 10 类分类任务。Mega-chunk 的分块大小为 1000。其他超参数列于表 8 中。

D.3 语言建模

训练细节
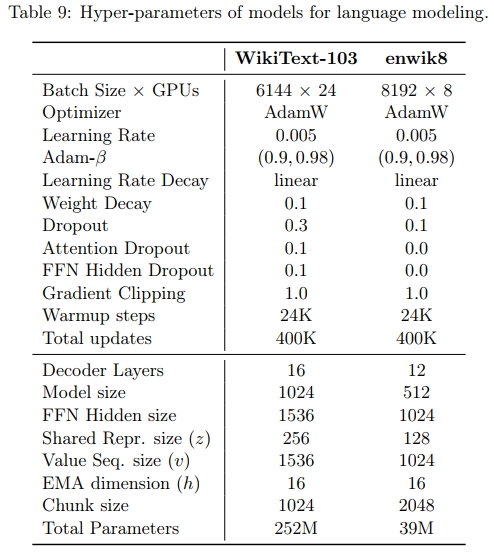
我们使用 WikiText-103 和 enwik8 的数据及其划分（由 Dai 等人于 2019 年提供）。在训练时，我们将训练数据分割成若干段；每段包含 m 个连续的分块，其中分块大小是有效的注意力长度。m 是一个从 [cl; ch] 中均匀采样的随机整数变量。对于 WikiText-103，我们使用 [cl; ch] = [2; 6]，而对于 enwik8，我们使用 [cl; ch] = [2; 4]。其他训练超参数（包括优化器、学习率调度器和架构）列于表 9 中。

推理时的长度外推
我们在训练时使用 Mega-chunk（§3.5），并将注意力分块大小分别设置为 1024（WikiText-103）和 2048（enwik8）。为了在推理时使用比训练时更长的 Mega 注意力长度（即 1024 或 2048），我们在注意力子层中应用了旋转位置嵌入（Su 等人，2021）。在测试时，我们将测试数据分割成 K 段，并依次处理每段的 m 个分块，即每段的最大上下文长度为 $\frac{\#\text{测试 token 数}}{K}$。在表 5 中，我们报告了使用更长分块大小（注意力长度）的测试结果，分别为 WikiText-103 的 2048 和 enwik8 的 4096。由于 EMA 层的循环设计，Mega 可以在推理时自然地外推到比训练时更长的序列。这种设计使得每个分块的输入可以通过 EMA 访问历史上下文，如图 3 所示。

另一方面，由于使用了旋转位置嵌入，注意力可以在测试时处理比训练时更长的分块大小。我们希望这两种长度外推方式对读者来说是清晰的。我们在下面提供了关于这两种长度外推方式的消融研究，即通过增加输入序列长度外推到更长的上下文，以及通过增加分块大小外推到更长的注意力长度。

上下文长度的消融实验

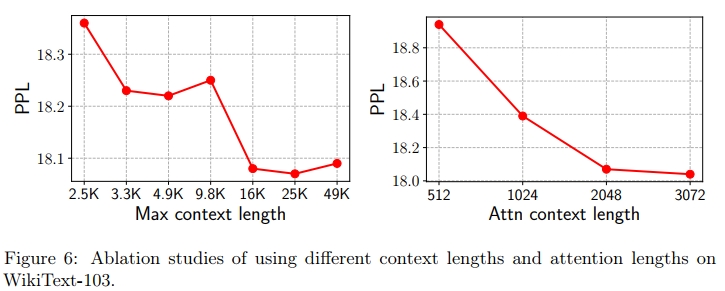
首先，我们将分块大小固定为 2048，并在 [100; 75; 50; 25; 15; 10; 5] 范围内调整 K，对应的最大上下文 token 数分别为 [2.5K; 3.3K; 4.9K; 9.8K; 16K; 25K; 49K]。我们在图 6 的左侧绘制了随着上下文长度增加时的测试 PPL（困惑度）。尽管在训练时模型所见的最大上下文长度为 6144，但 Mega 能够外推到更长的上下文长度。图中显示，随着上下文长度的增加，PPL 逐渐下降，并且当上下文长度超过 25K 时，改进趋于饱和。这一结果与 Press 等人（2021）的观察一致。

注意力分块大小的消融实验

接下来，我们将上下文长度固定为 25K，并将分块大小从 512 增加到 3072。如图 6 右侧所示，尽管 Mega 在训练时仅使用了 1024 的注意力长度，但随着注意力长度的增加，其性能持续提升。这一发现与 Alibi（Press 等人，2021）的研究结果相矛盾，Alibi 发现旋转位置嵌入无法泛化到更长的长度，并会导致更高的 PPL。

D.4 机器翻译

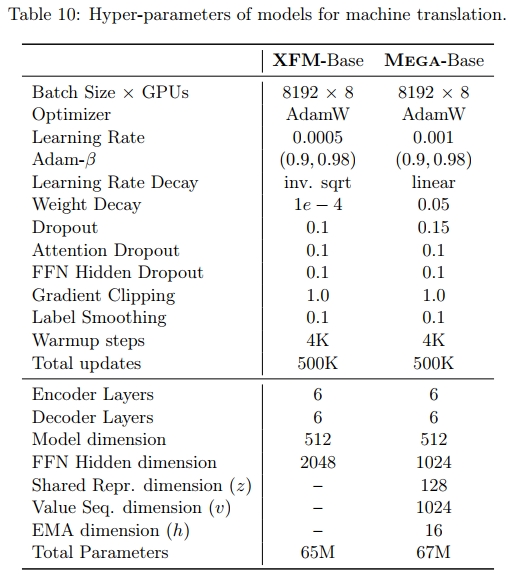
WMT 2016 英德数据集包含 450 万对平行句对用于训练。我们遵循标准设置（Ott 等人，2018），使用 Newstest2013 作为验证集，Newstest2014 作为测试集。数据集按照（Ma, 2020）的方法进行预处理，使用 FairSeq 包（Ott 等人，2019）中的脚本。我们在语言对内共享源语言和目标语言的词汇表，采用 32K 字节对编码（BPE）类型（Sennrich 等人，2016）。Transformer 和 Mega 模型的超参数列于表 10 中。

D.5 图像分类

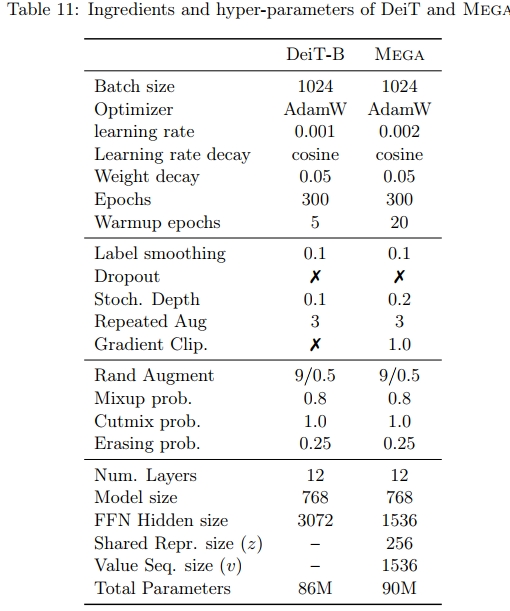
超参数列于表 11 中。我们严格遵循 Touvron 等人（2021）的研究，复用了他们的大部分超参数。