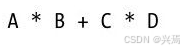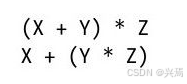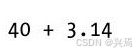【Python学习手册（第四版）】学习笔记05-Python对象类型-数字类型详解

在基本类型中，Python提供了：整数（正整数和负整数）和浮点数（带有小数部分的数字）。Python还允许我们使用十六进制、八进制和二进制常量来表示整数，提供一个复数类型，并且允许整数具有无穷的精度（只要内存空间允许，它可以增长成任意位数的数字）。表5-1展示了Python数字类型在程序中的显示方式（作为常量）。

整数和浮点数常量

整数以十进制数字的字符串写法出现。浮点数带一个小数点，也可以加上一个科学计数标志e或者E。如果编写一个带有小数点或幂的数字，Python会将它变成一个浮点数对象，并且当这个对象用在表达式中时，将启用浮点数（而不是整数）的运算法则。浮点数就像C语言中的“双精度”一样实现，因此，其精度与用来构建Python解释器的C编译器所给定的双精度一样。

Python 3.0中的整数：一个单独的类型

在Python 3.0中，一般整数和长整数类型已经合二为一了，只有整数这一种，它自动地支持Python 2.6的单独的长整数类型所拥有的无穷精度。因此，整数在程序中不再用末尾的l或L表示，并且整数也不再会显示出这个字符。

十六进制数、八进制和二进制常量

整数可以编写为十进制（以10为基数）、十六进制（以16为基数）、八进制（以8为基数）和二进制（以2为基数）形式。十六进制数以0x或0X开头，后面接十六进制的数字0～9和A～F。十六进制的数字编写成大写或小写都可以。八进制数常量以数字0o或0O开头（0和小写或大写的字母"o"），后面接着数字0～7构成的字符串。

所有这些常量在程序代码中都产生一个整数对象，它们仅仅是特定值的不同语法表示而已。内置函数hex(I)、oct(I)和bin(I)把一个整数转换为这3种进制表示的字符串，并且int(str,base)根据每个给定的进制把一个运行时字符串转换为一个整数。

复数

Python的复数常量写成实部+虚部的写法，这里虚部是以j或J结尾。其中，实部从技术上讲可有可无，所以可能会单独表示虚部。从内部看来，复数都是通过一对浮点数来表示的，但是对复数的所有的数字操作都会按照复数的运算法则进行。也可以通过内置函数complex(real,imag)来创建复数。

编写其他的数字类型

我们将在本章后面看到，还有表5-1中所没有包含的其他的、更高级的数字类型。其中的一些通过调用导入的模块中的函数来创建（例如，十进制数和分数），其他的一些拥有它们自己的常量语法（例如，集合）。

内置数学工具和扩展

除了在表5-1中显示的内置数字常量之外，Python还提供了一系列处理数字对象的工具：

表达式操作符

+、-、*、/、＞＞、**、＆等。

内置数学函数

pow、abs、round、int、hex、bin等。

公用模块

random、math等。

尽管数字主要是通过表达式、内置函数和模块来处理，它们如今也拥有很多特定于类型的方法，我们也将在本章中介绍这些。例如，浮点数拥有一个as_integer_ratio方法，它对于分数数字类型很有用；还有一个is_integer方法可以测试数字是否是一个整数。整数有各种各样的属性，包括一个将要在未来的Python 3.1中发布的新的bit_length方法，它给出表示对象的值所必需的位数。此外，集合既像一些集合一样也像一些数字一样，它也支持这两者的方法和表达式。

表达式是大多数数字类型最基本的工具，我们接下来将介绍它。

Python表达式操作符

表达式是处理数字的最基本的工具。当一个数字（或其他对象）与操作符相结合时，Python执行时将计算得到一个值。在Python中，表达式是使用通常的数学符号和操作符号写出来的。例如，让两个数字X和Y相加，写成X+Y，这就会告诉Python，对名为X和Y的变量值应用+的操作。这个表达式的结果就是X与Y的和，也就是另一个数字对象。

表5-2列举了Python所有的操作符表达式。

例如，is操作符测试对象身份（也就是内存地址，严格意义上的相等），lambda创建匿名函数。

在Python 3.0之中，值不相等测试使用X!=Y就行了。

在Python 3.0中，X/Y表达式执行真正的除法（保留余数）

Python 3.0删除了一个后引号表达式'X'和repr(X)的作用相同，转换对象以显示字符串。使用更容易理解的str和repr内置函数

·比较操作符可以连续使用：X＜Y＜Z的结果与X＜Y and Y＜X相同。参见本书后面的“比较：一般的和连续的”小节。

在Python 3.0中，非数字的混合类型的大小比较是不允许的，并且会引发异常，这包括按照代理排序。

·在Python 3.0中，对字典的大小比较也不再支持（尽管支持相等性测试）；比较sorted(dict.items())是一种可能的替代。

混合操作所遵循的操作符优先级

就像大多数语言一样，在Python中，将表5.2中的操作符表达式像字符串一样结合在一起就能编写出很多较复杂的表达式。例如，两个乘法之和可以写成变量和操作符的结合：

当编写含有一个操作符以上的表达式时，Python将按照所谓的优先级法则对其进行分组，这个分组决定了表达式中各部分的计算顺序。

·在表5-2中，表的操作符中越靠后的优先级越高，因此在混合表达式中要更加小心。

·表5-2中位于同一行的表达式在组合的时候通常从左到右组合（除了幂运算，它是从右向左组合的，还有比较运算，是从左到右连接的）。

括号分组的子表达式

如果用括号将表达式各部分进行分组的话，就可以完全忘掉优先级的事情了。当使用括号划分子表达式的时候，就会超越Python的优先级规则。Python总会先行计算括号中的表达式，然后再将结果用在整个表达式中

例如，表达式X+Y*Z写成下边两个表达式中的任意一个以此来强制Python按照你想要的顺序去计算表达式：

混合类型自动升级

除了在表达式中混合操作符以外，也能够混合数字的类型。例如，可以把一个整数与一个浮点数相加：

但是这将引出另一个问题：它们的结果是什么类型？是整数还是浮点数？答案很简单，特别是如果你有使用其他语言经验的话：在混合类型的表达式中，Python首先将被操作的对象转换成其中最复杂的操作对象的类型，然后再对相同类型的操作对象进行数学运算。

Python是这样划分数字类型的复杂度的：整数比浮点数简单，浮点数比复数简单。

可以通过手动调用内置函数来强制转换类型：

通常是没有必要这样做的。因为Python在表达式中自动升级为更复杂的类型，其结果往往就是你所想要的。

再者，要记住所有这些混合类型转换仅仅在将数字类型（例如，一个整数和一个浮点数）混合到一个表达式中的时候才适用，这包括那些使用数字和比较操作符的表达式。一般来说，Python不会在其他的类型之间进行转换。例如，一个字符串和一个整数相加，会产生错误，除非你手动转换其中某个的类型。

预习：运算符重载

要留心所有的Python操作符可以通过Python的类或C扩展类型被重载（即实现），让它也能工作于你所创建的对象中。例如，用类编写的对象代码也许可以使用+表达式做加法或连接，以及使用[i]表达式进行索引等。

再者，Python自身自动重载了某些操作符，能够根据所处理的内置对象的类型而执行不同的操作。例如，“+”操作符应用于数字时是在做加法，而用于字符串或列表这样的序列对象时是在做合并运算。实际上，“+”应用在定义的类的对象上可以进行任何运算。

这种特性通常称作多态。多态指操作的意义取决于所操作的对象的类型。

在实际应用中的数字

最好的理解数字对象和表达式的方法就是看看它们在实际中的应用。

变量和基本的表达式

练习一下基本的数学运算吧。在下面的交互中，首先把两个变量（a和b）赋值为整数，在更大的表达式中我们会使用它们。变量就是简单的名字（由你或Python创建），可以用来记录程序中信息。

在Python中：

·变量在它第一次赋值时创建。

·变量在表达式中使用将被替换为它们的值。

·变量在表达式中使用以前必须已赋值。

·变量像对象一样不需要在一开始进行声明。

换句话说，这些赋值会让变量a和b自动生成：

在#标记后直到本行末尾的文本会认作是一个注释并忽略。注释是为代码编写可读文档的方法。因为在交互模式下编写的代码是暂时的，一般是不会在这种情形下编写注释的，但是本书中的一些例子中添加了注释，是为了有助于解释代码。

让我们在表达式中使用新的整数对象。目前，a和b的值分别是3和4。一旦用在一个表达式中，就像这里的变量，都会被它们的值替换，当在交互模式下工作时，表达式的结果将马上显示出来：

>>> a + 1 , a - 1
(4, 2)
>>> b * 3, b /2
(12, 2.0)
>>> a % 2 ,b **2
(1, 16)
>>> 2 + 4.0 , 2.0 ** b
(6.0, 16.0)

从技术上讲，这里的回显所得到的结果是有两个值的元组，因为输入在提示符的那行包含了两个被逗号分开的表达式。显示的结果包含在括号里的原因。

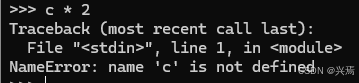
注意表达式正常工作了的，因为变量a和b已经被赋值了。如果使用一个从未被赋值的不同的变量，Python将会报告有错误而不是赋给默认的值：

在Python中，变量并不需要预声明，但是在使用之前，至少要赋一次值。实际上，这意味着在对其进行加法运算时要计数器初始化为0，在列表后添加元素前，要首先初始化列表为一个空列表。

>>> b / 2 + a
5.0
>>> print(b / (2 + a))
0.8

在第一个表达式中，没有括号，所以Python自动根据运算符的优先级法则将各部分分组。因为在表5-2中“/”比“+”位置靠后，它的优先级更高，所以首先进行“/”运算。结果就像代码右边的注释中加了括号表达式运算的结果一样。Python 3.0执行带有余数的真除法并且得到上面所示的结果。如果想要在Python 3.0中执行整数除法，把这段代码编写为b//2+a

在第二个表达式中，括号用在“+”的周围，强制使Python首先计算“+”（也就是说，先于“/”）。并且，通过增加小数点让其中的一个操作对象为浮点数2.0。因为是混合类型，Python在进行“+”之前首先将整数变换为浮点数的值（3.0）。

但在Python 3.0中得到浮点数0.8。

数字显示的格式

>>> num = 1/3.0
>>> num
0.3333333333333333
>>> print(num)
0.3333333333333333
>>> '%e' % num
'3.333333e-01'
>>> '%4.2f' % num
'0.33'
>>> '{0:4.2f}'.format(num)
'0.33'

这些方法中的最后三个使用了字符串格式化，这是灵活地进行格式化的一种工具

比较：一般的和连续的

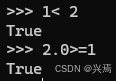
到目前为止，我们已经介绍了标准数字操作（加法和乘法），但是，还可以比较数字。一般的比较就像我们所期待的那样对数字起作用，它们比较操作数的相对大小，并且返回一个布尔类型的结果

str和repr显示格式

>>> num = 1/3
>>> repr(num)
'0.3333333333333333'
>>> str(num)
'0.3333333333333333'

这两个函数都会把任意对象变换成它们的字符串表示：repr（也就是默认的交互模式回显）产生的结果看起来就好像它们是代码。str（也就是打印语句）转变为一种通常对用户更加友好的格式。一些对象两种方式都有：str用于一般用途，repr用于额外细节。

除了为任意对象提供打印字符串，str内置函数也是字符串数据类型的名字，并且能够用一个编码的名字来调用，从而从一个字节字符串解码一个Unicode字符串。

在这里Python比较了更为复杂的类型（浮点类型）的值。

有趣的是，Python还允许我们把多个比较连续起来执行范围测试。连续的比较是更大的布尔表达式的缩写。简而言之，Python允许我们把大小比较测试连接起来，成为诸如范围测试的连续比较。例如，表达式(A＜B＜C)测试B是否在A和C之间；它等同于布尔测试(A＜B and B＜C)，但更容易辨识（和录入）。例如，假设如下的赋值：

>>> x = 2
>>> y = 4
>>> z = 6
>>> x<y<z
True
>>> x<y and y<z
True
>>> x<y>z
False
>>> 1<2<3.0<4
True
>>> 1>2>3.0<4
False

我们可以在连续测试中使用其他的比较，但是，最终的表达式可能变得很晦涩，除非你按照Python的方式来计算它们。

Python并不会把1==2的False的结果和3进行比较

>>> 1 == 2 < 3
False
>>> 1 == 2 and 2 < 3
False

除法：传统除法、Floor除法和真除法

X/Y 在Python 3.0版本中将会变成真除法（无论任何类型都会保持小数部分）

X//Y Floor除法。这个操作不考虑操作对象的类型，总会省略掉结果的小数部分，剩下最小的能整除的整数部分。

/和//操作符在Python 3.0中分别实现真除法和Floor除法。

·在Python 3.0中，/现在总是执行真除法，不管操作数的类型，都返回包含任何余数的一个浮点结果。//执行Floor除法，它截除掉余数并且针对整数操作数返回一个整数，如果有任何一个操作数是浮点类型，则返回一个浮点数。

>>> 3 //4
0
>>> 4 // 3
1
>>> 10 / 4.0
2.5
>>> 10 // 4.0
2.0

在Python 3.0中，//的结果的数据类型总是依赖于操作数的类型：如果操作数中有一个是浮点数，结果就是浮点数；否则，结果是一个整数。

Floor除法VS截断除法

一个细微之处在于：//操作符通常叫做截断除法，但是，更准确的说法是floor除法，它把结果向下截断到它的下层，即真正结果之下的最近的整数。其直接效果是向下舍入，并不是严格地截断，并且这对负数也有效。你可以使用Python的math模块来自己查看其中的区别：

>>> import math
>>> math.floor(2.5)
2
>>> math.floor(-2.5)
-3
>>> math.trunc(2.5)
2
>>> math.trunc(-2.5)
-2

在执行除法操作的时候，只是真正地截断了正的结果，因此截断除法和floor除法是相同的；对于负数，它就是一个floor结果（实际上，它们都是floor，但是对于正数来说，floor和截断是相同的）。

>>> 5/2 , 5/-2
(2.5, -2.5)
>>> 5//2, 5//-2
(2, -3)
>>> 5/2.0 , 5/-2.0
(2.5, -2.5)
>>> 5//2.0 , 5//-2.0
(2.0, -3.0)

如果你真的想要截断而不管符号，可以总是通过math.trunc来得到一个浮点除法结果

整数精度

除法可能在Python的各个版本中有所区别，但是，它仍然是相对标准的。

Python 3.0整数支持无穷的大小：

无穷大整数是一个方便的内置工具。例如，你可以使用它以美分为单位去直接计算年度预算（如果你有这种打算，并且计算机有足够多的内存）。

Python为了支持扩展的精度，需要做额外的工作，在实际应用中，长整型数的数学运算通常要比正常的整数运算（它是直接与硬件相关的）更慢。

复数

在Python中，复数是个不同的核心对象类型。

复数表示为两个浮点数（实部和虚部）并接在虚部增加了j或J的后缀。我们能够把非零实部的复数写成由+连接起来的两部分。例如，一个复数的实部为2并且虚部为-3可以写成2+-3j。下面是一些复数运算的例子。

>>> 1j * 1J
(-1+0j)
>>> 2 + 1j * 3
(2+3j)
>>> (2 + 1j ) * 3
(6+3j)

复数允许我们分解出它的实部和虚部作为属性，并支持所有一般的数学表达式，并且可以通过标准的cmath模块（复数版的标准数学模块）中的工具进行处理。复数通常在面向工程的程序中扮演重要的角色。

十六进制、八进制和二进制记数

Python整数能够以十六进制、八进制和二进制记数法来编写，作为一般的以10位基数的十进制记数法的补充。

记住，这些常量只是指定一个整数对象的值的一种替代方法。

>>> 0o1,0o20,0o377
(1, 16, 255)
>>> 0x01,0x10,0xFF
(1, 16, 255)
>>> 0b1,0b10000,0b11111111
(1, 16, 255)

八进制值0o377、十六进制值0xFF和二进制值0b11111111，都表示十进制的255。Python默认地用十进制值（以10为基数）显示，但它提供了内置的函数，允许我们把整数转换为其他进制的数字字符串：

>>> oct(64),hex(64),bin(64)
('0o100', '0x40', '0b1000000')

oct函数会将十进制数转换为八进制数，hex函数会将十进制转换为十六进制数，而bin会将十进制数转换为二进制。

内置的int函数会将一个数字的字符串变换为一个整数，并可以通过定义的第二个参数来确定变换后的数字的进制：

>>> int('64'),int('100',8),int('40',16),int('1000000',2)
(64, 64, 64, 64)
>>> int('0x40',16),int('0b1000000',2)
(64, 64)

eval函数，将会把字符串作为Python代码。因此，它也具有类似的效果（但往往运行得更慢：它实际上会作为程序的一个片段编译并运行这个字符串，并且它假设你能够信任运行的字符串的来源。）

>>> eval('64'),eval('0o100'),eval('0x40'),eval('0b1000000')
(64, 64, 64, 64)

最后可以使用字符串格式化方法调用和表达式将一个整数转换成八进制数和十六进制数的字符串：

>>> '{0:o},{1:x},{2:b}'.format(64,64,64)
'100,40,1000000'
>>> '%o,%x,%X' % (64,255,255)
'100,ff,FF'

在Python 3.0中必须使用0o010

其次，注意这些常量可以产生任意长度的整数。例如，下面的例子创建了十六进制形式的一个整数，然后先用十进制形式显示它，再将其转换为八进制和二进制的形式：

>>> x = 0xFFFFFFFFFFFFFFFFFFFFFFFFFF
>>> x
20282409603651670423947251286015
>>> oct(x)
'0o37777777777777777777777777777777777'
>>> bin(x)
'0b11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111'

位操作

除了一般的数学运算（加法、减法等），Python也支持C语言中的大多数数学表达式。这包括那些把整数当作二进制位串对待的操作。例如，还可以实现位移及布尔操作：

>>> x = 1
>>> x << 2
4
>>> x | 2
3
>>> x & 1
1

在第一个表达式中，二进制数1（逢2进位，0001）左移了两位，成为二进制数4（0100）。最后的两个操作一个是二进制或（0001|0010=0011），一个是二进制与（0001＆0001=0001）。这样的按位进行掩码的运算，使我们可以对一个整数进行多个标志位和值进行编码。

如果需要“位运算”的话，它是支持的，并且如果Python代码必须与由C程序生成的网络包或封装了的二进制数打交道的话，它是很实用的。尽管这样，注意位操作在Python这样的高级语言中并不像在C这样的底层语言中那么重要。作为一个简明的法则，如果你需要在Python中对位进行翻转，你应该想想现在使用的是哪一门语言。一般来说，在Python中有比位字符串更好的编码信息的方法。

Python 3.1中，整数的bit_length方法也允许我们查询以二进制表示一个数字的值所需的位数。通过bin和内置函数len（本书第4章介绍过）得到二进制字符串的长度，然后在减去2，我们往往可以得到同样的效果，尽管这种方法效率较低：

其他的内置数学工具

除了核心对象类型以外，Python还支持用于数字处理的内置函数和内置模块。例如，内置函数pow和abs，分别计算幂和绝对值。这里有一些内置math模块（包含在C语言中math库中的绝大多数工具）的例子并有一些实际中的内置函数。

>>> import math
>>> math.pi,math.e                    #π 跟e 
(3.141592653589793, 2.718281828459045)
>>> math.sin(2 * math.pi /180)        #sin函数
0.03489949670250097
>>> math.sqrt(144),math.sqrt(2)       #平方根
(12.0, 1.4142135623730951)
>>> pow(2,4),2 ** 4                #指数
(16, 16)
>>> abs(-42.0),sum((1,2,3,4))        #绝对值，求和
(42.0, 10)
>>> min(3,4,1,0),max(3,4,1,0)        #最小，最大
(0, 4)

sum函数作用于数字的一个序列，min和max函数接受一个参数序列或者单个的参数。

有各种各样的方法可以删除一个浮点数的小数位。我们前面介绍了截断和floor方法，我们也可以用round，

正如我们在前面看到的，最后一个例子产生了我们通常会打印出的字符串，并且它支持各种格式化选项。同样，如果我们把倒数第二行的例子包含到一个print调用中以要求一个更加用户友好的显示，它将会输出(3,2,2.57)。然而，最后两行还是有差异的，round舍入一个浮点数但是仍然在内存中产生一个浮点数，而字符串格式化产生一个字符串并且不会得到一个修改后的数字：

在Python中有3种方法可以计算平方根：使用一个模块函数（math.sqrt）、一个表达式（x ** .x）或者一个内置函数（pow（x, .x））

模块是外部的组件，而内置函数位于一个隐性的命名空间内，Python自动搜索程序的变量名。这个命名空间对应于Python 3.0中名为builtins的模块

使用标准库中的random模块时必须导入。这个模块提供了工具，可以选出一个在0和1之间的任意浮点数、选择在两个数字之间的任意整数、在一个序列中任意挑选一项等：

Random模块很实用，在游戏中的发牌、在演示GUI中随机挑选图片、进行统计仿真等都需要使用Random模块。

数字扩展

尽管Python的核心数字类型提供的功能对于大多数应用程序已经够用了，还是有大量的第三方开源扩展可以用来解决更加专门的需求。由于数字编程是Python的常用领域，你将会发现众多的高级工具。

如果你需要做一些正式的数字计算，一个叫做NumPy(Numeric Python)的可选的Python扩展提供了高级的数字编程工具，例如矩阵数据类型、向量处理和高级的计算库。

像Los Alamos和NASA这样的核心科学编程组织，使用带有NumPy的Python来实现此前用C++、FORTRAN、Matlab编写的任务。

Python和NumPy的组合往往可以比作是一款免费的、更加灵活的Matlab，可以得到NumPy的性能以及Python语言及其库。

你可以通过在Python的PyPI站点或者通过搜索Web，来找到对高级数字编程的其他支持，包括图形工具和绘制工具、统计库以及流行的SciPy包。另外，还要注意，NumPy目前是一个可选的扩展；还没有纳入到Python中，必须单独安装。

习题答疑

1.Python中表达式2*(3+4)的值是多少？

2.Python中表达式2*3+4的值是多少？

3.Python中表达式2+3*4的值是多少？

4.通过什么工具你可以找到一个数字的平方根以及它的平方？

5.表达式1+2.0+3的结果是什么类型？

6.怎样能够截断或舍去浮点数的小数部分？

7.怎样将一个整数转换为浮点数？

8.如何将一个整数显示成八进制、十六进制或二进制的形式？

9.如何将一个八进制、十六进制或二进制数的字符串转换成平常的整数？

习题解答

1.结果的值将会是14,即2*7的结果，因为括号强制让加法在乘法前进行运算。

2.这里结果会是10，即6+4的结果。Python的操作符优先级法则应用在没有括号存在的场合，根据表5-2，乘法的优先级要比加法的优先级高（先进行运算）。

3.表达式将得到14，即2+12的结果，正如前一个问题一样是优先级的原因。

4.求平方根、pi以及正切等等函数，在导入math模块后即可使用。为了找到一个数字的平方根，import math后调用math.sqrt(N)。为了得到一个数字的平方，使用指数表达式X**2，或者内置函数pow(X,2)。上述两种方式的任何一种也可以用来计算一个数的0.5次方（例如，X**.5）。

5.结果将是一个浮点数：整数将会变换升级成浮点数，这个表达式中最复杂的类型，然后使用浮点数的运算法则进行计算。

6.int(N)函数和math.trunc(N)函数会省略小数部分，而round(N，digit)函数做四舍五入。我们可以使用math.floor(N)来计算floor，并且使用字符串格式化操作来舍入以便于显示。

7.float(I)将整数转换为浮点数；在表达式中混合整数和浮点数也会实现转换。在某种意义上，Python 3.0的/除法也会转换，它总是返回一个包含余数的浮点数结果，即便两个操作数都是整数。

8.内置函数oct(I)和hex(I)会将整数以八进制数和十六进制数字符串的形式返回。%字符串表达式也会实现这样的目标。在Python 2.6和Python 3.0中，bin(I)也会返回一个数字的二进制数字字符串。%字符串格式化表达式和字符串格式化方法也为这样的转换提供方法。

9.int(S,base)函数能够用来让一个八进制和十六进制数的字符串转换为正常的整数（传入8、16或2作为base的参数）。eval(S)函数也能够用作这个目的，但是运行起来开销更大也有可能导致安全问题。注意整数总是在计算机内存中以二进制保存的；这些只不过是显示的字符串格式的转换而已。