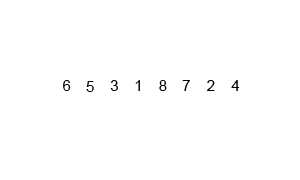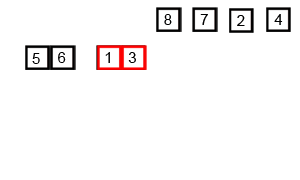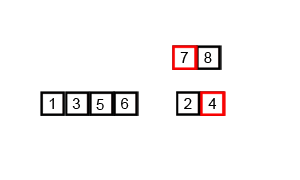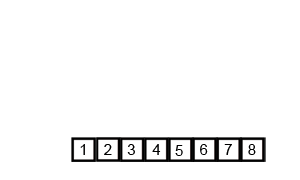目录
一:归并排序算法介绍
归并排序是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分解数组,再合并数组。将数组分解最小之后,然后合并两个有序数组,基本思路是比较两个数组的最前面的数,谁小就先取谁,取了后相应的指针就往后移一位。然后再比较,直至一个数组为空,最后把另一个数组的剩余部分复制过来即可。
二:归并排序的分析
三:归并排序的Python代码实现
def merge_sort(alist):
"""归并排序算法"""
n = len(alist)
if n <= 1:
return alist
# 二分分解
num = len(alist)//2
# left 采用归并排序后形成的有序的新的列表
left_li = merge_sort(alist[:num])
# right 采用归并排序后形成的有序的新的列表
right_li = merge_sort(alist[num:])
# 将两个有序的子序列合并成一个有序的整体
left_pointer, right_pointer = 0, 0 # 定义两个游标
result = [] # 定义一个空列表用于存放有序序列
while left_pointer< len(left_li) and right_pointer < len(right_li):
if left_li[left_pointer] < right_li[right_pointer]:
result.append(left_li[left_pointer])
left_pointer += 1
else:
result.append(right_li[right_pointer])
right_pointer += 1
# 如果左右数组长度不对称、直接将剩余的元素添加到result中
result += left_li[left_pointer:]
result += right_li[right_pointer:]
return result
if __name__ =="__main__":
alist = [54, 26, 93, 17, 77, 31, 44, 55, 20, 99]
print(alist)
sorted_alist = merge_sort(alist)
print(sorted_alist)运行结果:
四:算法时间复杂度分析
- 最优时间复杂度:O(nlogn)
- 最坏时间复杂度:O(nlogn)
- 稳定性:稳定
注:该算法的时间复杂度不易从代码中分析得到、可以通过分析其过程得到(类似于快速排序)
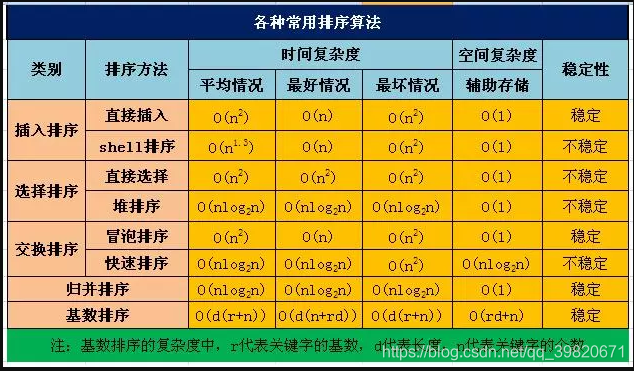
五:常见排序算法效率比较
排序算法(一)之冒泡排序(Python代码实现)
排序算法(二)之选择排序(Python代码实现)
排序算法(三)之插入排序(Python代码实现)
排序算法(四)之希尔排序(Python代码实现)
排序算法(五)之快速排序(Python代码实现)
排序算法(六)之归并排序(Python代码实现)