1 基本思想
我们求解常微分方程的时候,某些常微分方程有解析方法,但是大多数的常微分方程只能用数值解法来求解。
数值解法的一个基本特点就是“递进式”,顺着节点的顺序一步一步向前推进。
龙格库塔法的基本思想就是利用f(x,y)在某些特殊点上的函数值的线性组合,来估算高阶单步法的平均斜率。
1.1 平均斜率
对于常微分方程,有一个初始解y=y(x),用泰勒展开式有(其中,h=x(n+1)-x(n)):
根据拉格朗日中值定理,存在一个θ∈(0,1),使得
所以对于,有
y'(x+θh)就是这里的平均斜率。
2 二阶龙格库塔法
考虑区间上的点
(0<p≤1)
用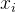
点的斜率K1和K2的加权平均作为
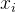
的 平均斜率K的近似值
即:K=λ1K1+λ2K2,也就是=
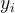
-
λ1和λ2都是待定的常数,K1=f(yi,yi),那么问题在于:如何确定点的斜率K2和常数λ1,λ2
按照改进的泰勒展开式,用泰勒展开式估计
(
(y'=f(x,y))
并用它来估计斜率K2
于是得到如下形式的算法:
要使得公式具备二阶精度,需要:
λ1+λ2=1—— h的系数
λ2p=1/2——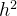
(和泰勒公式里面h的系数对应)
方程组有无穷多组解,所以二级方程有无穷多种。
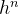
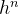
另一部分是这么看的:f(x,y+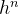
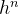
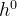
2.2 常用的二阶龙格库塔法
2.2.1 中点法
λ1=0,λ2=1 ,p=1/2
2.2.2 传统二阶龙格库塔法:
λ1=1/2 λ2=1/2 p=1
3 传统三阶龙格库塔法
通过验证,不难发现h的1,2,3次方的系数和泰勒展开式中一致
h的系数 1/6+2/3+1/6=1
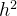
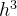
4 传统四阶龙格库塔法
4.1 四阶龙格库塔法举例
我们使用经典四阶龙格库塔法:
实验结果:
可视化结果











