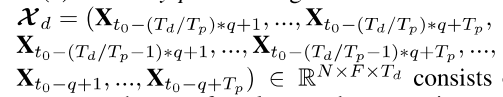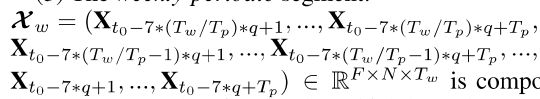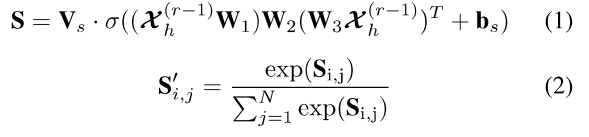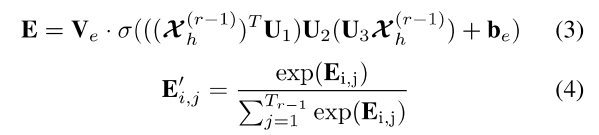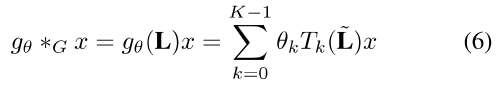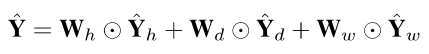AAAI2019
0 摘要
交通流数据通常有很高的非线性和很复杂的特征。目前很多交通预测的方法缺乏对交通数据时空相关性的动态建模。
本文提出了一种基于注意力的时空图卷积神经网络(ASTGCN)来解决交通预测问题
ASTGCN包括三个独立的部分,分别对交通流的三种时间属性进行建模:
1)当前相关性(recent dependencies)
2)每天的周期性(daily-periodic dependencies)
3)每周的周期性(weekly-periodic dependencies)
每个独立的部分都包含了以下两块:
1)时空注意力机制,可以捕捉交通数据中动态的时空相关性
2)时空卷积,可以同时将图卷积应用于交通数据中,来捕获时间和空间特征
单个独立部分的结果将被加以权重地结合起来,来生成最终的预测结果
1 introduction
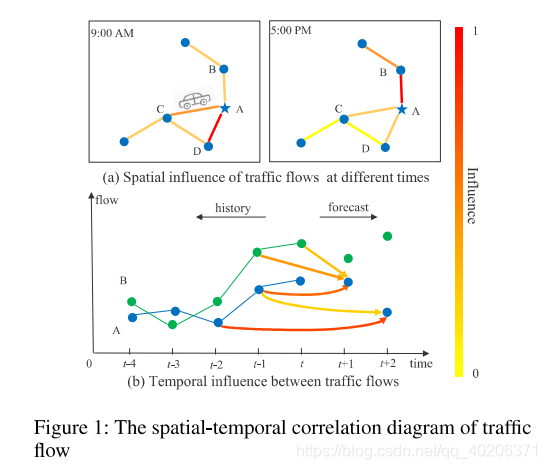
图1体现了交通数据的时空相关性,不同的位置,不同的时间,各点交通流量之间的影响是不一样的——》交通数据在空间和时间维度都展现出了强大的动态特征
早期模型的缺点
| 时间序列分析模型 | 难以解决数据的不稳定行和非线性 |
| 传统机器学习 | 1)难以同时考虑高维交通数据集中时空相关性 2)十分依赖特征的选择和建立 |
| 一些深度学习模型 | 仍然难以同时建模交通数据中时间和空间特征的相关性 |
ASTGCN:
1)使用空间注意力机制来建模空间层面复杂的相关性
2)使用时间注意力机制来捕获不同时间之间的动态时间相关性
3)使用图卷积来捕获交通图中的空间特征;以及不同时间篇之间的依赖关系
2 相关工作
2.1 交通预测
| 统计模型 | HA、ARIMA、VAR | 这些模型需要数据满足一些假设,但是交通数据过于复杂,无法满足这些假设,所以这些模型在交通预测领域的表现不尽人意 |
| 机器学习模型 | KNN,SVM | 这些模型需要进行自己的特征工程 |
| 深度学习模型 | ST-ResNet、CNN+LSTM | 数据必须是标准的2D,3D表格数据 |
2.2 GNN
| spatial methods | 直接在图上进行卷积计算 |
| spectral methods | 使用图拉普拉斯矩阵(切比雪夫多项式进行优化) |
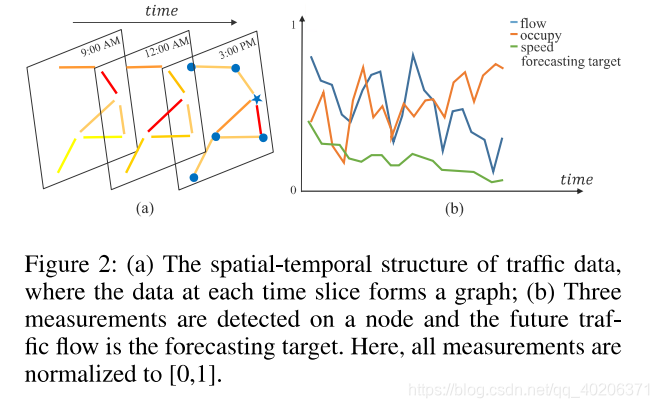
3 Preliminaries
3.1 交通网络
| G=(V,E,A) | 无向交通图 |
| V | 点集 |
| E | 边集 |
| F | 每个点的观测特征维度 |
3.2 交通流预测
问题描述
4 ASTGCN
4.1 整体框架
ASTGCN由三个部分组成(前面在abstract说的recent、daily-periodic和weekly-periodic),三个部分的结构几乎是一样的。
为了优化训练的效率,我们在每个ST模块上添加了一个残差连接
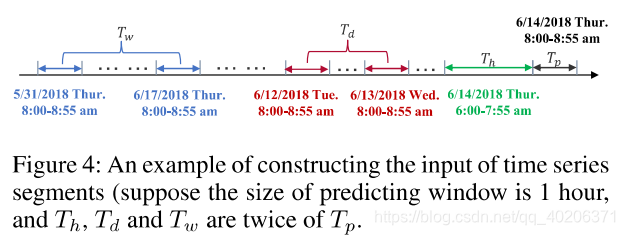
4.2 recent、daily-periodic和weekly-periodic数据集划分
我们分别设置提取数据集的时间片段长度Th,Td和Tw,表示recent、daily-periodic和weekly-periodic的数据集划分间隔,Th,Td,Tw都是原始数据集时间间隔的整数倍
4.2.1 recent 临近时间片段
预测时间段之前的一小段时间片段
4.2.2 daily 日周期片段
预测时间片段之前几天相同的时间片段
4.2.3 weekly 周时间片段
预测时间片段之前几周相同的时间片段
4.3 时空注意力机制
- 在空间维度,不同区域的交通状况相互影响,这种相互影响有很强的动态性
- 在时间维度,不同的时间片段的交通流量存在相关性
4.3.1 空间注意力机制
通过注意力机制捕获以上两种关系,此处以recent 模块为例:
这里
是第r层ST-块的输入
是第r层每个点每一时刻特征的维度(当r=1时,也就是原始输入,
等于F)
是第r层时间维度的长度(当r=1的时候,对于recent来说,
就是
;对于daily来说,
就是
;对于weekly来说,
就是
)
和
都是N×N的矩阵,是对attention结果的加权/bias
对应的是attention里面Q,K,V的权重,其中
机器学习笔记:Transformer_UQI-LIUWJ的博客-CSDN博客_机器学习transformer
、
、
都是可学习的参数
σ是激活函数
由此我们便动态地算出了本层ST模块的空间注意力矩阵,这个矩阵根据当前层ST模块的数据计算而得。
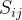
之后的图卷积模块中,我们会将这个空间注意力矩阵S和邻接矩阵A一起考虑,来动态调整点与点之间的影响权重
4.3.2 时间注意力机制
和空间注意力机制类似,我们有:
其中,这五个矩阵都是可学习的
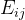
之后的图卷积中,我们直接将标准化的时间注意力矩阵应用到数据集上
来动态调整输入数据
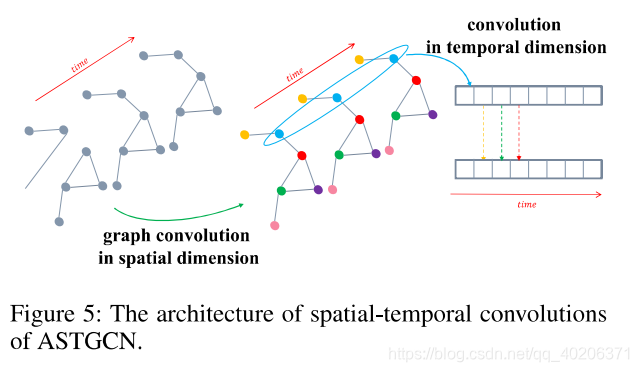
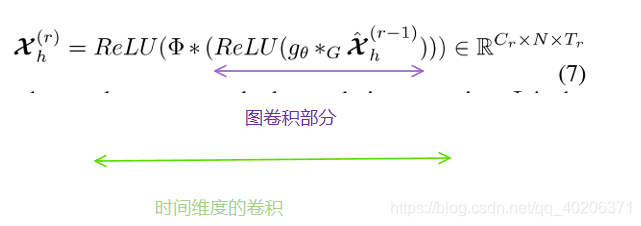
4.4 时空卷积
之前时空注意力模组让网络更关注一些更有用的信息。调整后的输入被喂入时空卷积中
时空卷积网络由一个空间维度的图卷积(来捕获邻居节点之间的依靠关系)和一个时间维度的卷积(来捕获相邻时间片之间的依靠关系)
4.4.1 空间维度的图卷积
这里使用谱图卷积(spectral graph convolution)。图结构的属性可以通过分析图拉普拉斯矩阵及其特征值来获得
拉普拉斯矩阵L=D-A,D是度矩阵(对角矩阵),A是邻接矩阵
标准拉普拉斯矩阵
对拉普拉斯矩阵进行特征值分解,我们有:
(这里因为是无向图,所以拉普拉斯矩阵一定对称,所以后面一项可以是U的转置)
其中:
是特征值组成的对角矩阵
U是傅里叶基
我们记图上的一个点的信号为x,那么这个信号x经过图傅里叶变化之后,变为:
因为拉普拉斯矩阵是对称矩阵,所以U是一个正交矩阵,所以信号x的逆拉普拉斯矩阵为
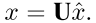
基于上面的部分,信号x和图上的filter 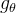
*G表示了一个图卷积计算
我们可以把上述方程看成:先把信号x和
经过傅里叶变化变换到谱图域中,然后将他们进行乘法操作,最后在通过你傅里叶变化得到最州的谱图卷积结果
然而,当图很大的时候,计算拉普拉斯矩阵的特征值开销是很大的,于是,我们可以使用切比雪夫多项式来进行近似:
这时候的参数θ就是切比雪夫多项式的系数了。
,
是拉普拉斯矩阵最大的特征值。
切比雪夫多项式为
我们进行0~k-1的切比雪夫多项式的相加,相当于计算0阶~k-1阶邻居节点对于中心节点的影响(影响的大小由卷积核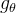
图卷积的觉果使用RELU进行激活,即
而我们在4.3.1引入了空间注意力机制,得到了一个空间注意力矩阵S‘,怎么使用那个矩阵呢?
对于切比雪夫多项式中的,我们让他和S’做哈达玛积(对应位置元素相乘),即:
那么“有价值”的点,获得的权重更多;“没有价值”的点,获得的权重就少
因此,在引入了空间注意力机制后,用切比雪夫多项式近似的谱图卷积可以写为:
4.4.2 时间维度的卷积
在图卷积之后,我们使用时间卷积来更新点的信号
4.4.3 ST卷积模块总结
时空注意力模块+时空卷积模块,组合成了一个ST卷积模块
我们可以叠加多个ST卷积模块,以进一步提取更大“感受野”的关联信息。
最后,添加一个全连接层,以保证输出与目标有相同的维度和形状,最后的全连接层使用 ReLU 作为激活函数。
4.5 Mult-component fusion:将recent、daily-periodic和weekly-periodic模块结果结合
这一个部分很简单
即三组可学习的参数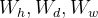
5 实验部分
5.1 数据预处理:
1)去除了冗余的观测点,使得相邻观测点之间的距离大于等于3.5英里(不知道为什么。。。)
2)缺失的点使用线性插值填充
3)数据用zero-mean来进行标准化
5.2 实验结论
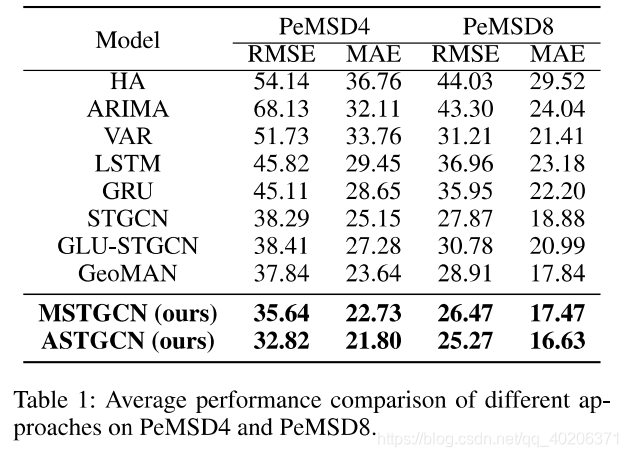
1)传统的时间序列分析方法(HA、ARIMA)通常并不理想
——>这些方法在建模交通数据的非线性和复杂性上是欠佳的
2)相比于传统的时间序列方法,有些深度学习的方法得到的结果会好很多
3)在深度学习方法中,同时考虑了时间和空间属性的模型(STGCN、GLU-STGCN、GeoMAN、我们的模型)效果比LSTM和GRU(只考虑了空间属性的模型)好
4)GeoMAN模型效果比STGCN和GLU-STGCN效果好
——>注意力机制是有效的
5)对我们的模型MSTGCN(没有注意力机制的模型)已经比原有的模型要好了;加了注意力机制之后的模型ASTGCN效果更好
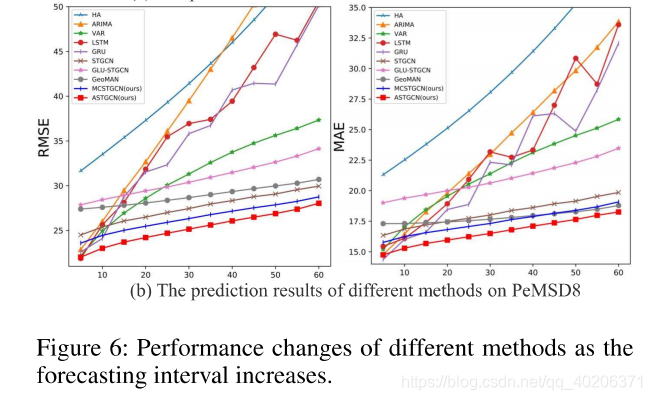
随着我们的预测间距的增大,预测的难度也在增加,预测误差也随之增加
只考虑时间属性的模型,在短期预测任务中通常有不粗的表现(HA、ARIMA、LSTM、GRU等),但是,随着预测区间的增发,这些模型不适用于预测长期的内容
相比而言,同类型模型的VAR准确率下降得就慢了很多。(因为VAR同时考虑了时间和空间的相关性,这个在长期预测任务中是很关键的),但是随着交通网络规模的增大,我们需要考虑更多的交通时序信息,,VAR的预测误差就上去了(如图6所示,VAR在PeMSD4的准确度小于其在PeMSD8的准确度)
我们的模型在任何时候都比其他的模型效果好,尤其是在长期预测问题中。这说明了使用注意力机制+图卷积操作可以更好地挖掘交通数据中动态的时空特征
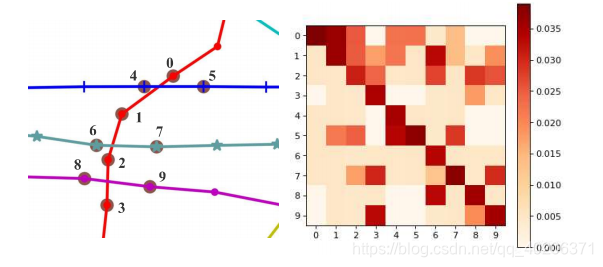
图7在说明注意力机制有什么用处,论文选取了PeMSD8中的10个点,对他们之间的attention矩阵进行了可视化。
以点9为例,权重大的是点3和点8,这是很合理的
6 展望
未来可以考虑一些外部影响因素,例如天气因素和大型事件,进一步提高预测精度。