第一题是基础打卡题，按照字符串匹配模拟即可。

第二题暴力枚举即可，数据比较小，当然也有优化方法

第一题：

输入描述

第一行是一个整数n，表示有n个函数名。接下来n行，每行一个字符串，保证每个字符串只包含小写字母和下划线，字符串长度均不超过30。

输出描述

输出n行，第i行表示按照问题描述中对输入中的第i个函数名的判断结果。

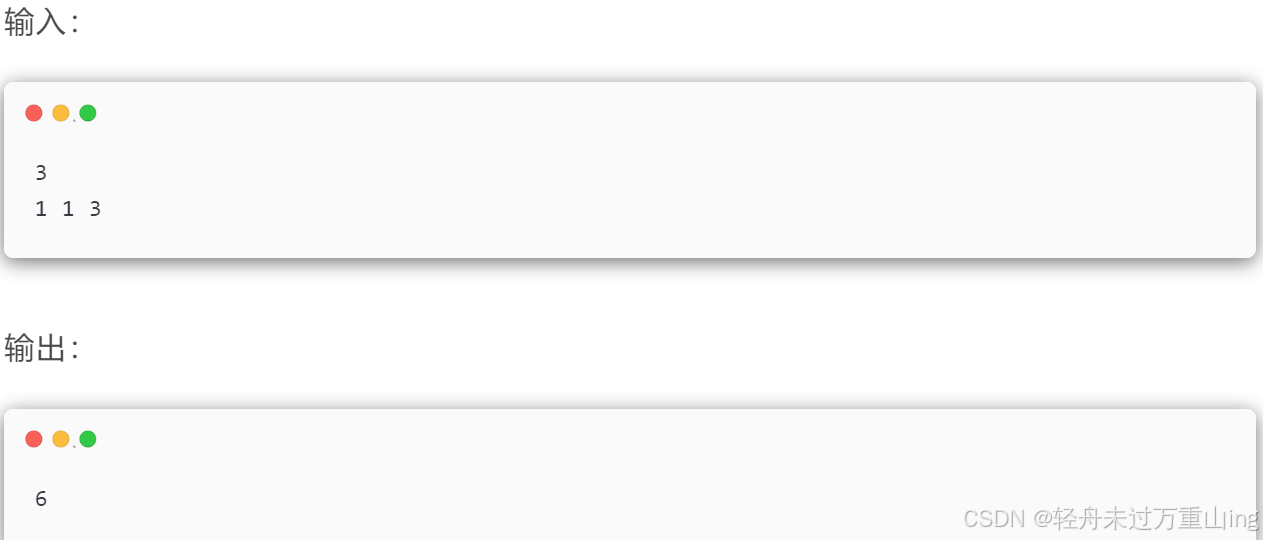
示例：输入：

输出：

思路与代码

这道题思路很简单，只需要按照题目意思模拟即可，这边主要三个步骤，分别为

1. 判断小驼峰命名法：遍历字符串，检查是否包含大写字母，第一个字母不能是大写字母。

2. 判断下划线命名法：检查字符串是否包含 _ 且全为小写字母，注意这边还不能出现两个下划线，以及最后一个字符不能是下划线。

3. 转换：将小驼峰命名法的字符串转换为下划线命名法， 这边直接遇到大写字母就变成下划线加上该大写字母的小写，否则不变。

通过对字符串的遍历和条件判断，合理判断和转换命名法格式，输出符合题意的结果。复杂度在可接受范围内，可以处理题目给定的输入规模。

参考答案：

import java.util.*;  // 导入Java集合框架的类

public class Main {

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);  // 创建Scanner对象用于读取输入
        int n = Integer.parseInt(sc.nextLine().trim()); //读取并解析输入的整数，表示名称的数量
        List<String> names = new ArrayList<>();  // 存放名称的列表
        for (int i = 0; i < n; i++) {  // 读取n个名称
            names.add(sc.nextLine().trim());  // 读取每一行并添加到列表中
        }
        List<String> results = convNames(names);  // 调用convNames方法进行转换
        for (String result : results) {  // 遍历并打印每一个结果
            System.out.println(result);
        }
    }

    // 转换名称列表，根据名称的格式进行不同的处理
    public static List<String> convNames(List<String> names) {
        List<String> res = new ArrayList<>();  // 存放结果的列表
        for (String name : names) {  // 遍历每一个名称
            if (isCamelCase(name)) {  // 如果是驼峰命名法
                res.add(camelToSnake(name));  // 转换为蛇形命名法并添加到结果中
            } else if (isSnakeCase(name)) {  // 如果是蛇形命名法
                res.add(name);  // 直接添加到结果中
            } else {
                res.add("indistinct");  // 如果不符合驼峰或蛇形命名法，添加"indistinct"
            }
        }
        return res;  // 返回结果列表
    }

    // 判断字符串是否符合驼峰命名法
    public static boolean isCamelCase(String name) {
        // 确保字符串不是全小写，没有下划线，且首字符是小写字母
        return !name.equals(name.toLowerCase()) && !name.contains("_") && Character.isLowerCase(name.charAt(0));
    }


    // 将驼峰命名法的字符串转换为蛇形命名法
    public static String camelToSnake(String name) {
        StringBuilder res = new StringBuilder();  // 使用StringBuilder构建结果字符串
        for (char ch : name.toCharArray()) {  // 遍历字符串的每一个字符
            if (Character.isUpperCase(ch)) {  // 如果字符是大写字母
                res.append('_').append(Character.toLowerCase(ch));  // 添加'_'和字符的小写形式到结果中
            } else {
                res.append(ch);  // 如果是小写字母，直接添加到结果中
            }
        }
        // 如果结果字符串以'_'开头，去掉第一个字符
        return res.charAt(0) == '_' ? res.substring(1) : res.toString();
    }

    
    // 判断字符串是否符合蛇形命名法
    public static boolean isSnakeCase(String name) {
        // 确保字符串是全小写，没有双下划线，且首尾字符都不是下划线
        return name.equals(name.toLowerCase()) && !name.contains("__") && name.charAt(name.length() - 1) != '_' && name.charAt(0) != '_';
    }

}

第二题：

输入描述

一行一个整数，表示房屋数量n。接下来1行，共n个整数，表示这n个房屋上的数值。

输出描述

一行一个整数表示方案数。

说明: 这里任意两个数字之间都有倍数关系。因此所有的六种情况均符合要求。

注意:1号房屋，2号房屋，3号房屋/2号房屋，1号房屋，3号房屋

上述两种排列尽管数值是一样的(排列后均为1，1，3)，但是两个不同的方案。

import java.util.*;  // 导入Java集合框架的类

public class Main {
    private static int size;  // 存储输入的整数个数
    private static int[] numbers;  // 存储输入的整数
    private static Integer[][] cache;  // 缓存用于动态规划的结果

    public static void main(String[] args){
        Scanner input = new Scanner(System.in);  // 创建Scanner对象用于读取输入
        size = input.nextInt();  // 读取整数个数
        numbers = new int[size];  // 初始化整数数组
        for(int index = 0; index < size; index++){
            numbers[index] = input.nextInt();  // 读取每一个整数并存储在数组中
        }
        // 初始化缓存，cache[i][j]存储以i为最后元素、状态为j的子集的数量
        cache = new Integer[size][1 << size];
        // 调用explore方法从深度0，状态0，最后元素-1开始进行探索
        System.out.println(explore(0,0,-1));
    }

    // 递归方法，用于计算以某种状态组合为基础的不同有效排列数
    private static int explore(int depth, int state, int last) {
        if(depth == size){  // 如果深度等于输入的整数个数
            return 1;  // 说明当前排列是有效的，返回1
        }
        // 如果缓存中有保存的结果，直接返回缓存中的值
        if(last != -1 && cache[last][state] != null){
            return cache[last][state];
        }
        int count = 0;  // 计数器，用于记录有效排列数
        for(int current = 0; current < size; current++){
            // 检查当前状态下，当前元素是否还未被使用
            if((state & (1 << current)) == 0){
                // 检查当前元素是否符合条件（当前是第一个元素，或者满足条件的组合）
                if(last == -1 || numbers[current] % numbers[last] == 0
                        || numbers[last] % numbers[current] == 0){
                    // 递归调用explore，增加深度、更新状态、将当前元素作为最后一个元素
                    count += explore(depth + 1, state | (1 << current), current);
                }
            }
        }
        // 如果last不为-1，缓存当前结果以供以后使用
        if(last != -1){
            cache[last][state] = count;
        }
        return count;  // 返回计算的有效排列数
    }
}

• main 方法:

  • 使用 Scanner 读取输入的整数个数 size。
  • 初始化 numbers 数组，并将输入的整数存储在数组中。
  • 初始化 cache 数组，其中 cache[i][j] 用于缓存以 i 为最后元素、状态为 j 的子集的有效排列数。
  • 调用 explore 方法进行深度优先搜索，从深度 0、状态 0、最后元素 -1 开始。

• explore 方法:

  • 递归终止条件: 当 depth 达到 size 时，说明当前排列是有效的，返回 1。
  • 缓存查找: 如果缓存中有保存的结果，则直接返回缓存中的值。
  • 循环遍历: 遍历所有可能的当前元素 current，检查当前元素是否符合条件（即未被使用且符合可连接条件）。
  • 递归调用: 递归调用 explore 方法，更新 depth、state 和 last。
  • 缓存结果: 如果 last 不为 -1，将计算结果存储在 cache 中。
  • 返回结果: 返回计算的有效排列数。