一项综述类的课程作业
Anomaly detection with generative adversarial networks for multivariate time series.
MAD-GAN: Multivariate anomaly detection for time series data with generative adversarial networks.
TAnoGAN: Time Series Anomaly Detection with Generative Adversarial Networks.
TadGAN: Time Series Anomaly Detection Using Generative Adversarial Networks.
基于GAN框架的时间序列异常检测研究综述
1 背景
在许多现实世界的系统(例如智能建筑,工厂,发电厂和数据中心)中,网络传感器和执行器的普及为这些系统生成了大量的多元时间序列数据。这些网络物理系统(CPS)中的许多都是为执行关键任务而设计的,因此成为网络攻击的目标。可以通过一些异常检测方法连续监视这类时间序列数据是否存在入侵事件。时间序列异常检测的目的是在时间序列中分离出不同长度的异常子序列。最简单的检测技术之一是阈值化,它检测超出正常范围的数据点。由于缺少标签信息,通常将时间序列数据中的异常检测作为无监督的机器学习任务来处理。一种流行的方法包括将时间序列分段为一定长度的子序列(重叠或其他形式),并应用聚类算法来查找异常值。另一个学习一种预测或重建时间序列信号的模型,并在真实值与预测或重建值之间进行比较。较高的预测或重建误差表明存在异常。
生成对抗网络(GAN)框架通过对抗训练来学习生成模型正变得越来越流行。 GAN模型可以成功生成逼真的图像和合成数据。它已被用来模拟现实世界中时间序列数据的复杂且高维的一般(即正态)分布[1]。生成对抗网络在图像处理任务中已经有了不错的成绩,但对于时间序列数据采用GAN框架的工作还十分有限。最近几年,逐渐有学者尝试将GAN框架用于异常检测[2-6]。
本篇综述的目的有以下两个方面:首先,介绍了最近提出的基于GAN框架进行时间序列异常检测的一些研究方法,并比较了不同研究方法之间的异同点。然后回顾了这些方法在不同数据集下的实验,对实验结果进行了分析。
2 基于GAN的时间序列异常检测方法
时间序列异常被定义为系统表现异常的时间点或时间段。点异常是指达到异常值的单个数据点,而时间段异常是指作为一个整体被认为是异常的连续数据点序列,即使单个数据点可能并不异常。它们可能有一些据称是“正常”的时间点,但在它们发生的特定时间是不寻常的,即时间段异常。
传统的异常检测方法无法处理由现代信息物理系统(CPS)日益动态和复杂的性质所产生的多元数据流。而受监督的机器学习方法由于缺少标记数据而无法利用大量数据。此外,当前的无监督机器学习方法是通过线性投影和变换构建的,还没有完全利用时空相关性和系统中用于检测异常的多个变量之间的其他依赖性。大多数当前技术是采用了当前状态与预测的正常范围之间的简单比较来进行异常检测。鉴于系统的高度动态性,这可能是不够的。MAD-GAN[4]、TAnoGAN[5]和TadGAN[6]几种基于生成对抗网络(GAN)的无监督时间序列异常检测方法相继被提出。下面分别对这三种方法进行介绍。
2.1 MAD-GAN
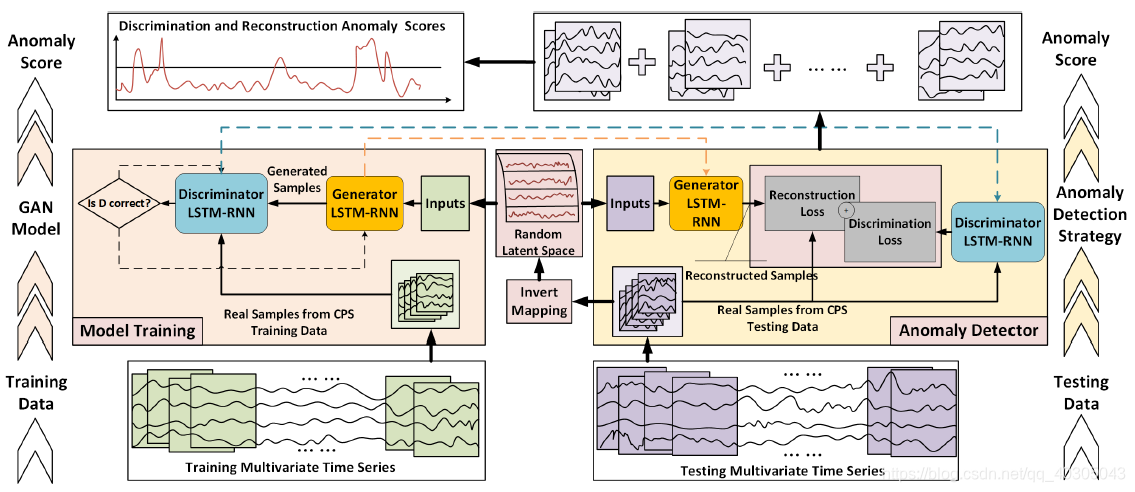
首先,为了处理时间序列数据,论文将GAN的生成器和判别器构造为两个长短期循环神经网络(LSTM-RNN),如图2.1左中部分所示。按照典型的GAN框架,生成器(G)以来自随机潜在空间的序列作为输入,生成假的时间序列,并将生成的序列样本传递给判别器(D),判别器将尝试将生成的数据序列与实际的正常训练数据序列区分开来。
MAD-GAN框架不是独立地处理每个数据流,而是同时考虑整个变量集,以便将变量之间的潜在的交互作用捕捉到模型中。论文将多元时间序列划分为一个滑动窗口的子序列,然后再进行识别。在训练阶段,根据D的输出结果更新D和G的参数(式2.1),生成器G将捕捉到训练序列的隐藏多元分布。同时,判别器D也能够以较高的灵敏度区分假的(即异常)数据和真实的(即正常)数据。最后论文结合判别和重构定义异常分数DR-Score,如式2.2。其中,测试样本在时间t的残差计算如式2.3。
min
G
max
D
V
(
D
,
G
)
=
E
x
∼
p
d
a
t
a
(
X
)
[
log
D
(
x
)
]
+
E
z
∼
p
z
(
Z
)
[
log
(
1
−
D
(
G
(
z
)
)
)
]
(2.1)
\min \limits _G \max \limits _D V(D,G) = \mathcal {E}_{x\sim p_{data}(X)}\left[ \log D(x)\right] + \mathcal {E}_{z\sim p_z(Z)}\left[ \log (1-D(G(z)))\right] \tag{2.1}
GminDmaxV(D,G)=Ex∼pdata(X)[logD(x)]+Ez∼pz(Z)[log(1−D(G(z)))](2.1)
L j , t t e s = λ R e s ( X j , t t e s ) + ( 1 − λ ) H ( D r n n ( X j , t t e s ) , 1 ) (2.2) \displaystyle L_{j,t}^{tes}=\lambda Res(X^{tes}_{j,t})+(1-\lambda )\mathcal {H}(D_{rnn}(X^{tes}_{j,t}),1) \tag{2.2} Lj,ttes=λRes(Xj,ttes)+(1−λ)H(Drnn(Xj,ttes),1)(2.2)
R e s ( X j , t t e s ) = ∑ i = 1 T ∣ x j , t t e s , i − G r n n ( Z j , t k , i ) ∣ (2.3) Res(X^{tes}_{j,t})=\sum _{i=1}^T \mid x_{j,t}^{tes,i}-G_{rnn}(Z^{k,i}_{j,t}) \mid \tag{2.3} Res(Xj,ttes)=i=1∑T∣xj,ttes,i−Grnn(Zj,tk,i)∣(2.3)
2.2 TAnoGAN
与MAD-GAN非常相似,TAnoGAN仍然使用LSTM作为生成器和判别器模型来处理时间序列数据。不同的是,TAnoGAN使用了不同的有效架构来检测小数据集的异常。为了解决少量数据点问题,论文研究了多种生成器和判别器的架构。论文指出:当数据集较小时,较大的判别器很容易对数据进行过度拟合,而浅层的生成器无法生成足够真实的数据来击败判别器。
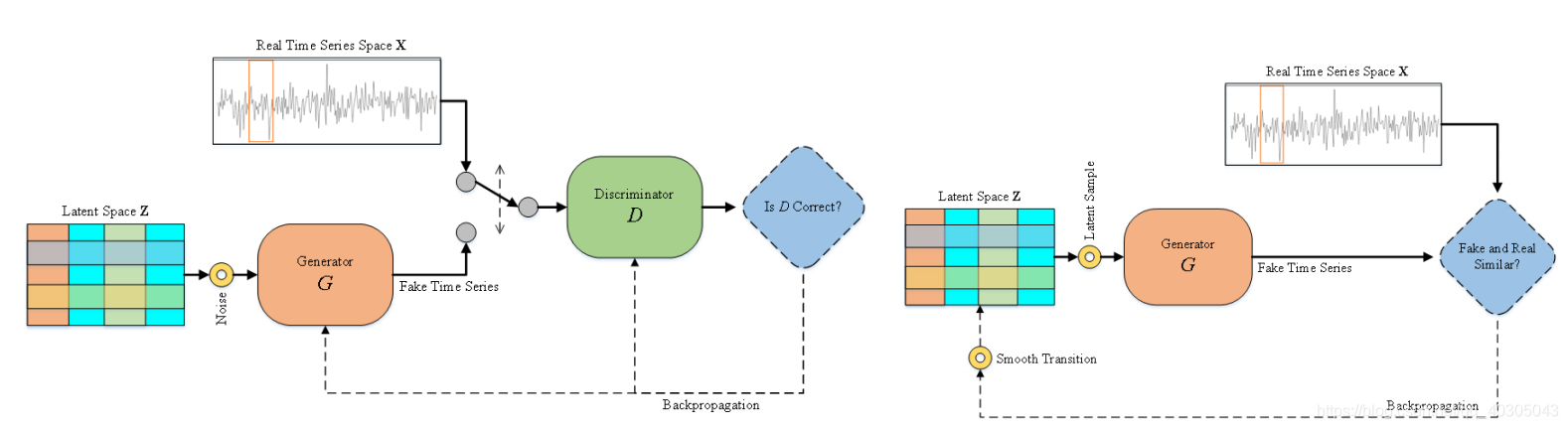
TAnoGAN方法分为“Learning General Data Distribution”和“Mapping Real-Data to the Latent Space”两个子处理过程。在第一个子过程(图2.2左)中,学习了基于生成对抗网络(GAN)的表示正常时间序列多样性的模型。在此子过程之后,生成器可以从潜在空间生成逼真的(假的)时间序列。在第二个子过程(图2.2右)中,我们将真实的时间序列映射到一个潜在空间,并从该潜在空间重构序列。
损失函数
L
L
L包括残差损失
L
R
\mathcal{L}_{R}
LR和判别损失
L
D
\mathcal{L}_{D}
LD,残差损失
L
R
\mathcal{L}_{R}
LR衡量的是真实的子序列
x
x
x和假子序列
G
(
z
λ
)
G(\mathrm{z}_{\lambda})
G(zλ)之间的逐点差异,如式2.4:
L
R
(
z
λ
)
=
∑
∣
x
−
G
(
z
λ
)
∣
(2.4)
\displaystyle \mathcal{L}_{R}(\mathrm{z}_{\lambda})=\sum|\mathrm{x}-G(\mathrm{z}_{\lambda})| \tag{2.4}
LR(zλ)=∑∣x−G(zλ)∣(2.4)
判别损失定义如式2.5:
L
D
(
z
λ
)
=
∑
∣
f
(
x
)
−
f
(
G
(
z
λ
)
)
∣
(2.5)
\displaystyle \mathcal{L}_{D}(\mathrm{z}_{\lambda})=\sum|f(\mathrm{x})-f(G(\mathrm{z}_{\lambda}))| \tag{2.5}
LD(zλ)=∑∣f(x)−f(G(zλ))∣(2.5)
损失函数
L
L
L被定义为如下的残差损失和判别损失的加权和,如式2.6:
L
(
z
λ
)
=
(
1
−
γ
)
⋅
L
R
(
z
λ
)
+
γ
⋅
L
D
(
z
λ
)
(2.6)
\mathcal{L}(\mathrm{z}_{\lambda})=(1-\gamma)\cdot \mathcal{L}_{R}(\mathrm{z}_{\lambda})+\gamma\cdot \mathcal{L}_{D}(\mathrm{z}_{\lambda}) \tag{2.6}
L(zλ)=(1−γ)⋅LR(zλ)+γ⋅LD(zλ)(2.6)
损失函数
L
L
L会评估假序列
G
(
z
λ
)
G(z_{\lambda})
G(zλ)与实际序列
x
x
x的不相似性。可以从
L
L
L直接得出表示给定
x
x
x与一般数据分布(即正常小序列模型)的拟合度的异常分数
A
(
x
)
A(x)
A(x),如式2.7:
A
(
x
)
=
(
1
−
γ
)
⋅
R
(
x
)
+
γ
⋅
D
(
x
)
(2.7)
A(\mathrm{x})=(1-\gamma)\cdot \mathcal{R}(\mathrm{x})+\gamma\cdot \mathcal{D}(\mathrm{x}) \tag{2.7}
A(x)=(1−γ)⋅R(x)+γ⋅D(x)(2.7)
2.3 TadGAN
论文指出应用标准对抗损失的原始公式存在梯度不稳定和模式崩溃的问题。模式崩溃是指在生成器与判别器的动态博弈之后,生成器其实是更倾向于产生那些已经被发现是“好”的样本来愚弄判别器,而不愿意产生新的样本,这导致生成器产生的样本多样性不足,无法完美收敛到目标分布。因此,TadGAN的目标包括Wasserstein loss和Cycle consistency loss。前者是为了使生成的时间序列的分布与目标域的数据分布相匹配;后者是为了防止两个生成器之间产生矛盾。
对于映射函数
G
:
Z
→
X
G:Z\rightarrow X
G:Z→X及其判别器
C
x
C_{x}
Cx,我们有目标如式2.8:其中,是
P
X
\mathbb{P}_{X}
PX上的分布。
C
x
\mathbb{C}_{x}
Cx表示利普希茨连续函数的集合。判别器的输出是输入时间序列为真实序列的概率,那么式2.9的目标就是使真实的时间序列的输出概率最大,生成的时间序列的输出概率最小。按照类似的方法,论文引入了映射函数及
ε
:
X
→
Z
\varepsilon :X\rightarrow Z
ε:X→Z其判别器
C
z
C_{z}
Cz的损失(式2.10)。
m
i
n
G
m
a
x
C
x
∈
C
x
V
X
(
C
x
,
G
)
(2.8)
min_{G}max_{C_{x}\in\mathbb{C}_{x}}V_{X}(C_{x},G) \tag{2.8}
minGmaxCx∈CxVX(Cx,G)(2.8)
V X ( C x , G ) = E x ∼ P X [ C x ( x ) ] − E z ∼ P Z [ C x ( G ( x ) ) ] (2.9) V_{X}(C_{x},G)=E_{x\sim \mathbb{P}_{X}}[C_{x}(x)]-E_{z\sim \mathbb{P}_{Z}}[C_{x}(G(x))] \tag{2.9} VX(Cx,G)=Ex∼PX[Cx(x)]−Ez∼PZ[Cx(G(x))](2.9)
m i n ε m a x C z ∈ C z V Z ( C z , ε ) (2.10) min_{\varepsilon}max_{C_{z}\in\mathbb{C}_{z}}V_{Z}(C_{z},\varepsilon) \tag{2.10} minεmaxCz∈CzVZ(Cz,ε)(2.10)
TadGAN的目的是为了重构输入的时间序列,但是仅仅使用对抗损失,不能保证将单个输入
x
i
x_{i}
xi映射到期望的输出
z
i
z_{i}
zi。于是论文又引入了Cycle Consistency Loss(式2.11),通过最小化原始样本和重构样本之间差异的
L
2
L2
L2范数,训练
ε
\varepsilon
ε和两
G
G
G个生成器。此外,论文指出,实验结果表明,添加反向一致性损失并没有改善模型的性能。
V
L
2
(
ε
,
G
)
=
E
x
∼
P
X
[
∥
x
−
G
(
ε
(
x
)
)
∥
2
]
(2.11)
V_{L2}(\varepsilon ,G)=E_{x\sim \mathbb{P}_{X}}[\left \| x-G(\varepsilon (x))\right \|_{2}] \tag{2.11}
VL2(ε,G)=Ex∼PX[∥x−G(ε(x))∥2](2.11)
结合上述所有目标,可以得到最终的minmax目标,如式2.12。
m
i
n
{
ε
,
G
}
m
a
x
{
C
x
∈
C
x
,
C
z
∈
C
z
}
V
X
(
C
x
,
G
)
+
V
Z
(
C
z
,
ε
)
+
V
L
2
(
ε
,
G
)
(2.12)
min_{\{\varepsilon ,G\}}max_{\{C_{x}\in\mathbb{C}_{x},C_{z}\in\mathbb{C}_{z}\}}V_{X}(C_{x},G)+V_{Z}(C_{z},\varepsilon)+V_{L2}(\varepsilon,G) \tag{2.12}
min{ε,G}max{Cx∈Cx,Cz∈Cz}VX(Cx,G)+VZ(Cz,ε)+VL2(ε,G)(2.12)
关于如何计算每个时间点的重构误差,论文提出了三种不同类型的函数。分别是逐点差、面积差和动态时间归整。判别器的输出是重构的时间序列为真实序列的概率,所以除了重构误差,判别器的输出也可以直接作为时间序列的异常指标。论文探讨了凸组合以及相乘两个将重构误差和判别器输出合并为异常分数的方法。
获得了每个时间点的异常分数后,论文用局部自适应阈值寻找异常序列,并提出一种异常修剪方法来减少误报。
2.4 方法间的异同点
2.4.1 相同点
-
MAD-GAN、TAnoGAN以及TadGAN均为基于重构的异常检测方法,其核心思想是学习一个能够对数据点进行编码的模型,然后对编码后的进行解码(即重构后的一段时间序列)。一个有效的模型不应该像 "正常 "实例一样能够重建异常,因为异常会在编码过程中丢失信息。
-
为了捕捉时间序列分布的时间相关性,MAD-GAN、TAnoGAN以及TadGAN均使用LSTM作为生成器和判别器模型来处理时间序列数据。
2.4.2 不同点
- 与MAD-GAN不同的是,TAnoGAN使用了不同的有效架构来检测小数据集的异常。
- 与MAD-GAN和TAnoGAN不同的是,TadGAN没有应用标准对抗损失的原始公式,而是结合Wasserstein loss和Cycle consistency得到最终的minmax目标。此外,TadGAN使用几种新的方法来计算重建误差,以及不同的方法来结合重建误差和判别器是输出来计算异常分数。
3 实验结果
3.1 实验概况
为了衡量MAD-GAN、TAnoGAN以及TadGAN的性能,各位学者均使用丰富多样的数据集与一些基准模型进行了大量的实验,如表3.1:
| model | DATASETS | baseline |
|---|---|---|
| MAD-GAN | the Secure Water Treatment (SWaT) and the Water Distribution (WADI) datasets | PCA、KNN、FB、AE、EGAN |
| TAnoGAN | 46 real-world time series datasets that cover a variety of domains | MAD-GAN、AutoEn、VanLstm、IsoF、GMM、OCSvm、BiLstmGan、CnnGan |
| TadGAN | 11 datasets from multiple reputable sources such as NASA, Yahoo, Numenta, Amazon, and Twitter | LSTM、Arima、DeepAR、LstmAE、HTM、DenseAE、MAD-GAN、MS Azure |
3.2 实验结果对比
3.2.1 TAnoGAN & MAD-GAN
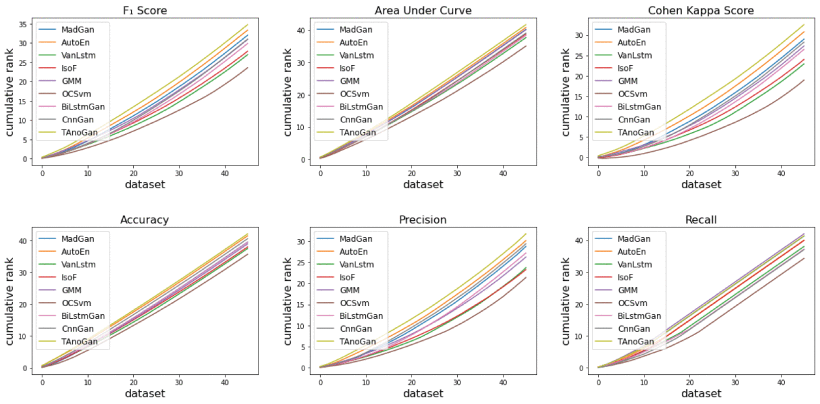
为了衡量TAnoGAN方法的有效性,论文进行了大量的实验。通过计算所有数据集中所有模型的累积排名可以显示TAnoGAN与基线模型的相对排名。图3.1显示,TAnoGAN在F1 score,Cohen Kappa Score,Precision,Accuracy和AUC方面均高于所有基线模型(包括MAD-GAN)。
其中,MAD-GAN,BiLstmGan[7]和CnnGan[2]与TAnoGAN具有相似的体系结构。通过在生成器中使用逐渐增加的隐藏单元数量,TAnoGAN比这些在生成器的所有内部层中使用相同数量的隐藏单元的模型性能更好。前面几层的隐藏单元数量少,可以解码序列的细粒度属性,后面几层的隐藏单元数量多,可以解码序列的粗粒度属性。这种架构可以实现序列的分层解码,允许关注序列不同抽象层次的属性变化。由于小数据集没有足够的实例,学习不同抽象层次的属性变化有助于生成器的泛化。
由表3.1可知,论文共使用了46个不同领域的数据集评估TAnoGAN。当评价的数据集数量较多时,临界差值对模型性能排名是有效的[8],分数越低性能越好。因此,论文绘制了临界差分图,如图3.2:
从上图可以看到,TAnoGAN在除Recall之外的所有评价指标中都优于所有基线方法。TAnoGAN的召回率接近GMM,优于其他模型。即使GMM的召回率略优于TAnoGAN,但GMM与TAnoGAN相比,F1 score较差。这说明GMM输出了大量的假阳性,导致精度很低(精度图也显示了同样的情况)。在异常检测中,较好的召回率是可取的,但过多的假阳性导致调查许多误报的成本较高。需要在召回率和精度两方面取得平衡,由较高的F1 score可以看出,TAnoGAN实现了这一点。
3.2.2 TadGAN & MAD-GAN
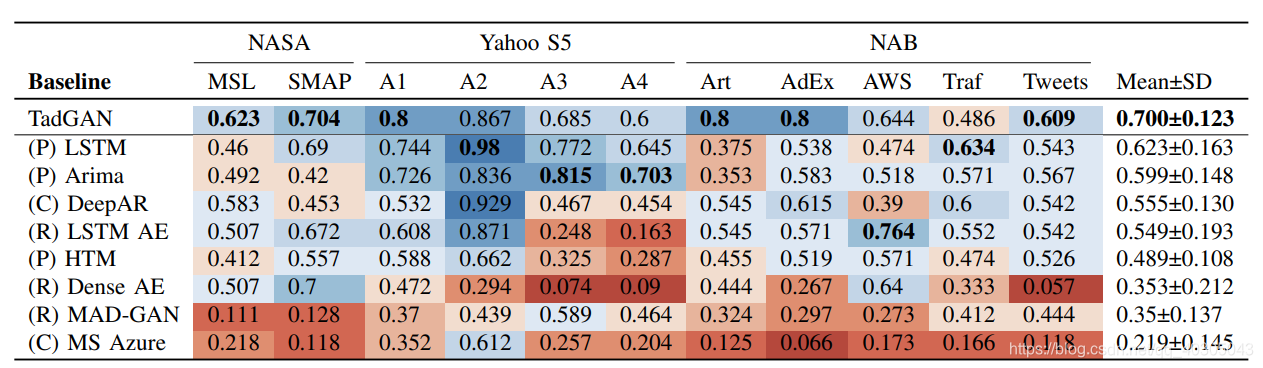
在MAD-GAN的基础上,TadGAN应用Wasserstein loss和Cycle consistency loss,避免了标准对抗损失的原始公式梯度不稳定和模式崩溃的问题。TadGAN与一些基于预测的模型、基于重构的模型以及商业工具的性能比较如图3.3:
从上图可以看到,TadGAN在所有数据集中具有最高的平均F1 score(0.7),优于所有基线方法。TadGAN(0.7)明显优于Mad-GAN(0.35)。这充分说明了Cycle Consistency Loss的使用,防止了两个生成器之间的矛盾,并保证测试样本 x i x_{i} xi对应最优的 z i z_{i} zi。
4 总结
本文介绍了最近提出的基于GAN框架进行时间序列异常检测的MAD-GAN、TAnoGAN以及TadGAN三种研究方法,并比较了不同研究方法之间的异同点。本文总结发现:(1)TAnoGAN在MAD-GAN的基础上使用了更有效的架构来检测小数据集的异常;(2)为避免MAD-GAN中标准对抗损失的原始公式梯度不稳定和模式崩溃的问题,TadGAN结合了Wasserstein loss和Cycle consistency loss两项子目标。然后本文还回顾了这些方法在不同数据集下的实验,着重对实验结果中的MAD-GAN、TAnoGAN以及TadGAN进行了分析。
基于GAN框架进行时间序列异常检测有一定的优势,但本人在实际应用中发现这类模型超参数普遍较多,也许在未来工作中可以对这类模型继续完善。此外,现实系统通常是源源不断地产生数据,异常也不是一成不变的。因此,有必要进行人工干预来纠正检测结果,再利用专家提供的正确的标签反馈到模型中。模型主动学习到数据的变化,也能获得更加准确的结果。
参考文献
[1] Esteban, Cristóbal, Stephanie L. Hyland, and Gunnar Rätsch. “Real-valued (medical) time series generation with recurrent conditional gans.” arXiv preprint arXiv:1706.02633 (2017).
[2] Schlegl, Thomas, et al. “Unsupervised anomaly detection with generative adversarial networks to guide marker discovery.” International conference on information processing in medical imaging. Springer, Cham, 2017.
[3] Li, Dan, et al. “Anomaly detection with generative adversarial networks for multivariate time series.” arXiv preprint arXiv:1809.04758 (2018).
[4] Li, Dan, et al. “MAD-GAN: Multivariate anomaly detection for time series data with generative adversarial networks.” International Conference on Artificial Neural Networks. Springer, Cham, 2019.
[5] Bashar, Md Abul, and Richi Nayak. “TAnoGAN: Time Series Anomaly Detection with Generative Adversarial Networks.” 2020 IEEE Symposium Series on Computational Intelligence (SSCI). IEEE, 2020.
[6] Geiger, Alexander, et al. “TadGAN: Time Series Anomaly Detection Using Generative Adversarial Networks.” arXiv preprint arXiv:2009.07769 (2020).
[7] Zhu, Fei, et al. “Electrocardiogram generation with a bidirectional LSTM-CNN generative adversarial network.” Scientific reports 9.1 (2019): 1-11.
[8] Fawaz, Hassan Ismail, et al. “Deep learning for time series classification: a review.” Data Mining and Knowledge Discovery 33.4 (2019): 917-963.