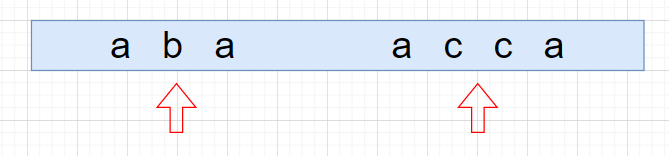Manacher (马拉车算法)
算法功能
回文字符串的通俗定义是:如果一个字符串正着读或反着读都一样,那么称这个字符串为回文字符串。
Manacher的作用就是在==O(N)==的时间复杂度下求出以每个位置为回文中心的最长回文半径。
前置知识
回文中心
此时发现如果回文字符串长度为偶数时,回文中心不能恰好落到某个数组下标处,为了统一操作,在每个字符中间添加一个特殊字符,如:
最长回文半径
以 i i i下标为回文中心的回文半径,可以理解为人的臂长。例如 上图红色的4
注意:有的资料中是把回文中心本身也计入回文半径的长度(在上图基础上每个回文半径+1),相比之下我更喜欢不计入的方式。因为这样无论字符串长度是奇数还是偶数,其最长回文长度,就是 m a x ( r [ i ] ) max(r[i]) max(r[i])
核心思想
暴力中心扩展
如果用暴力匹配&中心扩展的方式,遍历到每一个字符时都以该字符作为回文中心向两侧进行扩展,扩展的最大步数,即为以该点为回文中心的回文半径,时间复杂度 O ( n 2 ) O(n^2) O(n2)
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int r[105];
//将字符之间填充#字符,方便统一操作
string GetNewStr(string &str) {
string s = "#";
for (int i = 0; str[i]; ++i) {
(s += str[i]) += '#';
}
return s;
}
int main() {
string str;
cin >> str;
str = GetNewStr(str);
for (int i = 0; str[i]; ++i) {
while (i - r[i] >= 0 && str[i - r[i]] == str[i + r[i]]) ++r[i];
--r[i]; //将自身减掉
}
for (int i = 0; str[i]; ++i) {
printf("%3c", str[i]);
}
printf("\n");
for (int i = 0; str[i]; ++i) {
printf("%3d", r[i]);
}
printf("\n");
return 0;
}
/*
aba
# a # b # a #
0 1 0 3 0 1 0
acca
# a # c # c # a #
0 1 0 1 4 1 0 1 0
*/
优化
Manacher的核心思想就是尽可能借助之前已知的回文串,来减少以当前点为回文中心向两侧扩展的操作次数
我们发现,暴力方法在扫描完 s t r [ 4 ] str[4] str[4]后其实已经知道了 s t r [ 0 − 8 ] str[0-8] str[0−8]为回文串了。那么在扫描str[5]时,可以利用与当前已知可以向右扩展最远的回文中心(4)的对称点3的回文长度来减少扫描str[5]的操作次数
扫描str[i] 即是以str[i]作为回文中心向两侧探索
说人话就是:
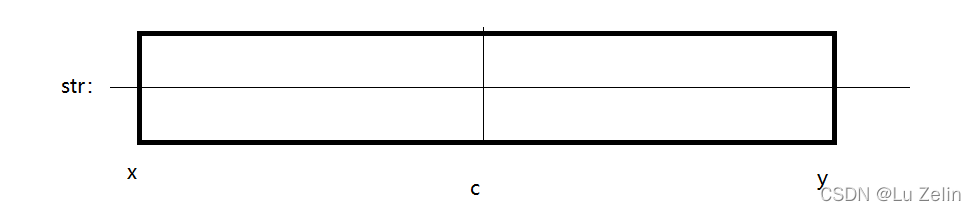
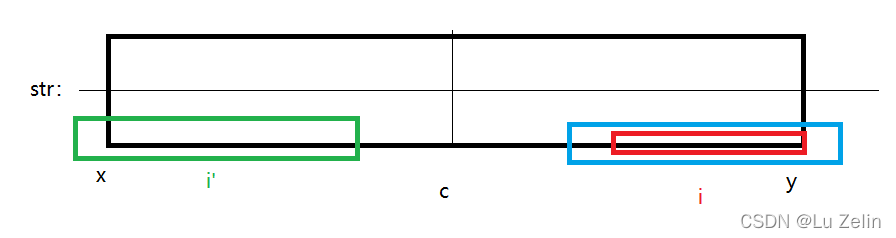
- 扫描完 c c c下标字符后,已经发现了 x x x~ y y y是回文串,并且在这之前没有扫描过哪个回文串的右边界> y y y。也就是说当前以 c c c下标作为回文中心的回文串,是向右扩展最远的
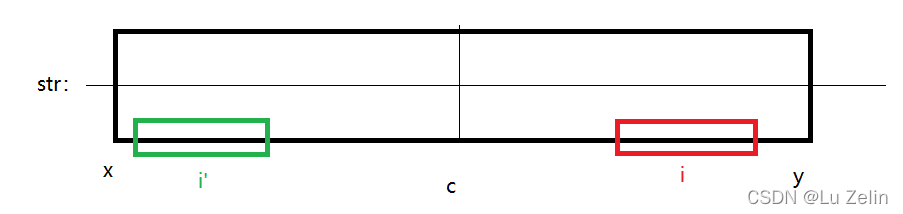
- 此时又探索到了 i i i下标位置,发现 i i i下标,还在当前已知最远回文串中。这时就可以利用 i i i基于 c c c的对称点 i ’ i’ i’的值来减少 i i i点向两侧扩展的次数
(1)第一种情况, r [ i ′ ] r[i'] r[i′]并没有超出 x x x~ y y y,所以 r [ i ] = r [ i ′ ] r[i] = r[i'] r[i]=r[i′]
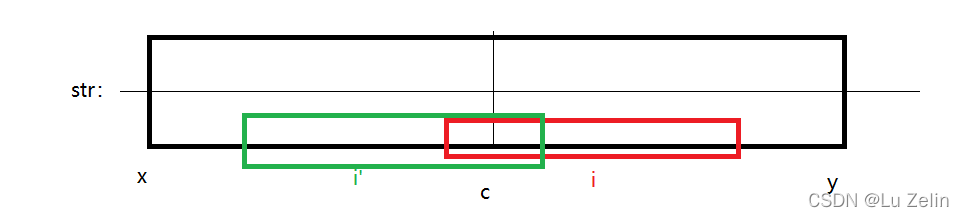
(2)第二种情况, r [ i ′ ] r[i'] r[i′]并超出x~y,所以 r [ i ] = c + r [ c ] − i r[i] = c + r[c] - i r[i]=c+r[c]−i
- 再通过暴力向两侧扩展 r [ i ] r[i] r[i]
- 经过优化之后,就可以借助之前的回文串,从而减少当前点的扫描扩展次数。注意过程中记录更新 c c c的位置
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
string Get_new(string &str) {
string temp = "#";
for (int i = 0; str[i]; ++i) {
(temp += str[i]) += "#";
}
return temp;
}
int main() {
string str;
cin >> str;
str = Get_new(str);
int *r = (int *)calloc(sizeof(int), str.size()), c = 0, ans = 0;
for (int i = 1; str[i]; ++i) {
if (c + r[c] > i) r[i] = min(r[2 * c - i], c + r[c] - i);
while (i - r[i] >= 0 && str[i - r[i]] == str[i + r[i]]) ++r[i];
--r[i];
if (i + r[i] > c + r[c]) c = i; //注意更新C的位置
ans = max(ans, r[i]);
}
cout << ans << endl;
free(r);
return 0;
}
时间复杂度证明
我们考虑产生复杂度的地方,分别是最外层对整个字符串的遍历和每次对回文串扩展的while。
显然,最外层的for循环是O(N)的,那么我们只需要证明while的总循环次数也是O(N)级别的即可。
1、如果以i位置的为回文中心的回文串的基础长度没有超出当前回文串的最大覆盖范围,那么显然不会进入while中(由于对称性,该回文串的长度已经最大了)。
2、如果以i位置的为回文中心的回文串的基础长度超出了当前回文串的最大覆盖范围,那么显然每进入一次while,回文串的最大覆盖范围都会加1.那么,当最大覆盖范围包含了整个字符串之后,while循环就不会在进入了。所以while循环的总次数为O(N)。综上所述,Manacher算法的时间复杂度为O(N)。
例题:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int Mod = 19930726;
const int N = 1e6;
int r[N + 5], cnt[N + 5], c = 0;
int quick_pow(long long n, long long p) {
int ans = 1;
while (p) {
if (p & 1) ans = (ans * n) % Mod;
n = (n * n) % Mod;
p >>= 1;
}
return ans % Mod;
}
int main() {
int n, max_len = 0;
long long m;
string str;
cin >> n >> m >> str;
for (int i = 0; str[i]; ++i) {
if (c + r[c] > i) r[i] = min(r[2 * c - i], c + r[c] - i);
while (i - r[i] >= 0 && str[i - r[i]] == str[i + r[i]]) ++r[i];
--r[i];
++cnt[1];
--cnt[r[i] * 2 + 2];
max_len = max(max_len, r[i] * 2 + 1);
if (i + r[i] > c + r[c]) c = i;
}
for (int i = 1; i <= max_len; ++i) {
cnt[i] += cnt[i - 1];
}
long long ans = 1;
for (int i = max_len; i > 0 && m; i -= 2) {
if (m >= cnt[i]) {
ans = (ans * quick_pow(i, cnt[i])) % Mod;
m -= cnt[i];
} else {
ans = (ans * quick_pow(i, m)) % Mod;
m = 0;
}
}
if (m) cout << -1 << endl;
else cout << ans << endl;
return 0;
}
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N = 2e5;
int r[N + 5], Left[N + 5], Right[N + 5], c;
string Get_new(string &str) {
string temp = "#";
for (int i = 0; str[i]; ++i) {
(temp += str[i]) += "#";
}
return temp;
}
int main() {
string str;
cin >> str;
str = Get_new(str);
for (int i = 0; str[i]; ++i) {
if (c + r[c] > i) r[i] = min(r[2 * c - i], c + r[c] - i);
while (i - r[i] >= 0 && str[i - r[i]] == str[i + r[i]]) ++r[i];
--r[i];
if (c + r[c] < i + r[i]) c = i;
Left[i + r[i]] = max(Left[i + r[i]], max(r[i], 1));
Right[i - r[i]] = max(Right[i - r[i]], max(r[i], 1));
}
for (int i = 2; i < (int)str.size(); i += 2) {
Right[i] = max(Right[i], Right[i - 2] - 2);
}
for (int i = str.size() - 3; i > 0; i -= 2) {
Left[i] = max(Left[i], Left[i + 2] - 2);
}
/*
for (int i = 0; str[i]; ++i) {
printf("%3c", str[i]);
}
printf("\n");
for (int i = 0; str[i]; ++i) {
printf("%3d", r[i]);
}
printf("\n");
for (int i = 0; str[i]; ++i) {
printf("%3d", Left[i]);
}
printf("\n");
for (int i = 0; str[i]; ++i) {
printf("%3d", Right[i]);
}
printf("\n");
*/
int ans = 0;
for (int i = 2; i < (int)str.size() - 1; i += 2) {
ans = max(ans, Left[i] + Right[i]);
}
cout << ans << endl;
return 0;
}