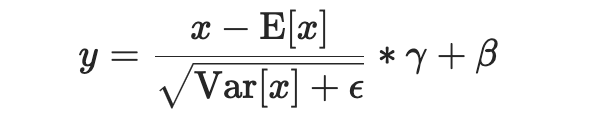1 nn.BatchNorm
BatchNorm是深度网络中经常用到的加速神经网络训练,加速收敛速度及稳定性的算法,是深度网络训练必不可少的一部分,几乎成为标配;
BatchNorm 即批规范化,是为了将每个batch的数据规范化为统一的分布,帮助网络训练, 对输入数据做规范化,称为Covariate shift;
数据经过一层层网络计算后,数据的分布也在发生着变化,因为每一次参数迭代更新后,上一层网络输出数据,经过这一层网络参数的计算,数据的分布会发生变化,这就为下一层网络的学习带来困难 -- 也就是在每一层都进行批规范化(Internal Covariate shift),方便网络训练,因为神经网络本身就是要学习数据的分布;
下面通过代码掩饰BatchNorm的作用;
首先要清楚,BatchNorm后是不改变输入的shape的;
nn.BatchNorm1d: N * d --> N * d
nn.BatchNorm2d: N * C * H * W -- > N * C * H * W
nn.BatchNorm3d: N * C * d * H * W --> N * C * d * H * W
下面讲解nn.BatchNorm1d,和nn.BatchNorm2d的情况
1.1 nn.BatchNorm1d
首先看其参数:
CLASStorch.nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True,
track_running_stats=True, device=None, dtype=None)主要参数介绍:
num_features: 输入维度,也就是数据的特征维度;
eps: 是在分母上加的一个值,是为了防止分母为0的情况,让其能正常计算;
affine: 是仿射变化,将,分别初始化为1和0;
使用方法介绍:
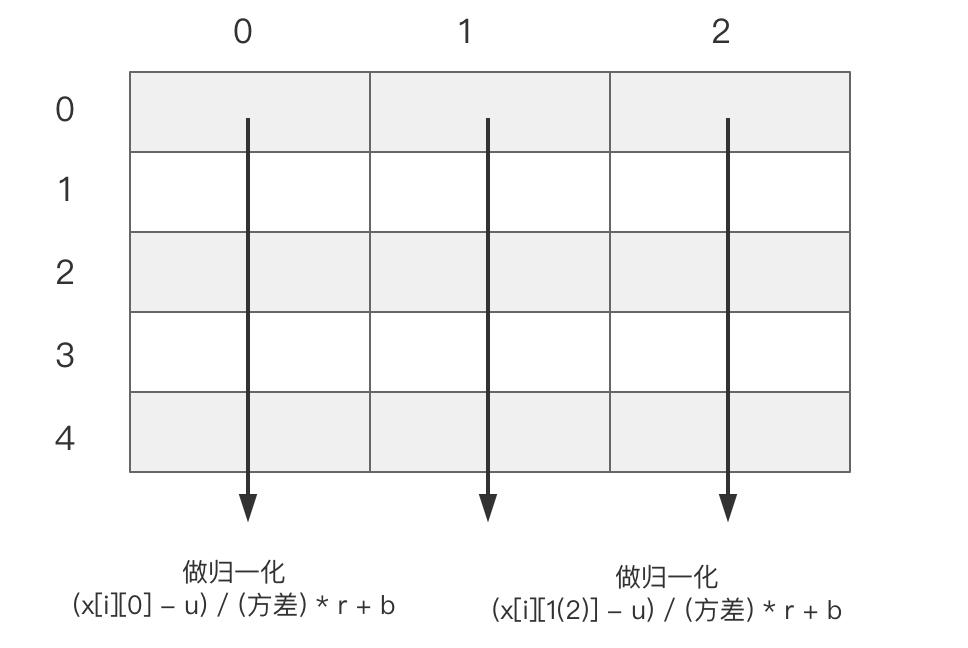
主要作用在特征上,比如输入维度为N*d, N代表batchsize大小,d代表num_features;
而nn.BatchNorm1d是对num_features做归一化处理,也就是对批次内的特征进行归一化;
如输入 N = 5(batch_size = 5), d = 3(数据特征维度为3);
上图中的r, b是可学习的参数,文档中成为放射变换,文档中称为, 可以使用x.weight 和 x.bias获得, r初始化值为1,b初始化值为0;
上图中方差的计算是采用的有偏估计;
归一化处理公式:
E(x)表示均值, Var(x)表示方差;表示为上述参数的eps,防止分母为0 的情况;
演示代码:
>>> import torch
>>> import torch.nn as nn
m = nn.BatchNorm1d(3) #首先要实例化,才能使用,3 对应输入特征,也就是number_features
>>> m.weight # 对应r ,初始化值为1
Parameter containing:
tensor([1., 1., 1.], requires_grad=True)
>>> m.bias # 对应b,初始化为0
Parameter containing:
tensor([0., 0., 0.], requires_grad=True)
>>> output.mean(dim = 0) # 归一化后,平均值都是0, e-08 实际上也就是0了
tensor([ 0.0000e+00, -1.1921e-08, -2.3842e-08], grad_fn=<MeanBackward1>)
>>> output.std(dim = 0,unbiased = False) # 标准差为1, 有偏估计,所以unbiased = False
tensor([1.0000, 1.0000, 1.0000], grad_fn=<StdBackward0>)
采用普通方法实现BatchNorm:
>>> x
tensor([[ 0.0482, -0.1098, 0.4099],
[ 0.9851, 2.8229, -0.7795],
[ 0.3493, -1.0165, -0.0416],
[ 1.5942, -1.3420, 1.0296],
[ 0.0452, -1.0462, -1.1866]])
>>> mean = x.mean(dim = 0)
>>> mean
tensor([ 0.6044, -0.1383, -0.1136])
>>> std = torch.sqrt(1e-5 + torch.var(x,dim = 0, unbiased = False))
>>> std
tensor([0.6020, 1.5371, 0.7976])
>>> (x - mean)/std
tensor([[-0.9239, 0.0185, 0.6564],
[ 0.6325, 1.9265, -0.8348],
[-0.4238, -0.5713, 0.0903],
[ 1.6442, -0.7831, 1.4333],
[-0.9290, -0.5906, -1.3452]])
>>> m(x) # 和上述计算结果相同
tensor([[-0.9239, 0.0185, 0.6564],
[ 0.6325, 1.9265, -0.8348],
[-0.4238, -0.5713, 0.0903],
[ 1.6442, -0.7831, 1.4333],
[-0.9290, -0.5906, -1.3452]], grad_fn=<NativeBatchNormBackward0>)
1.2 nn.BatchNorm2d
首先看其参数:
CLASStorch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True,
track_running_stats=True, device=None, dtype=None)使用方法介绍:
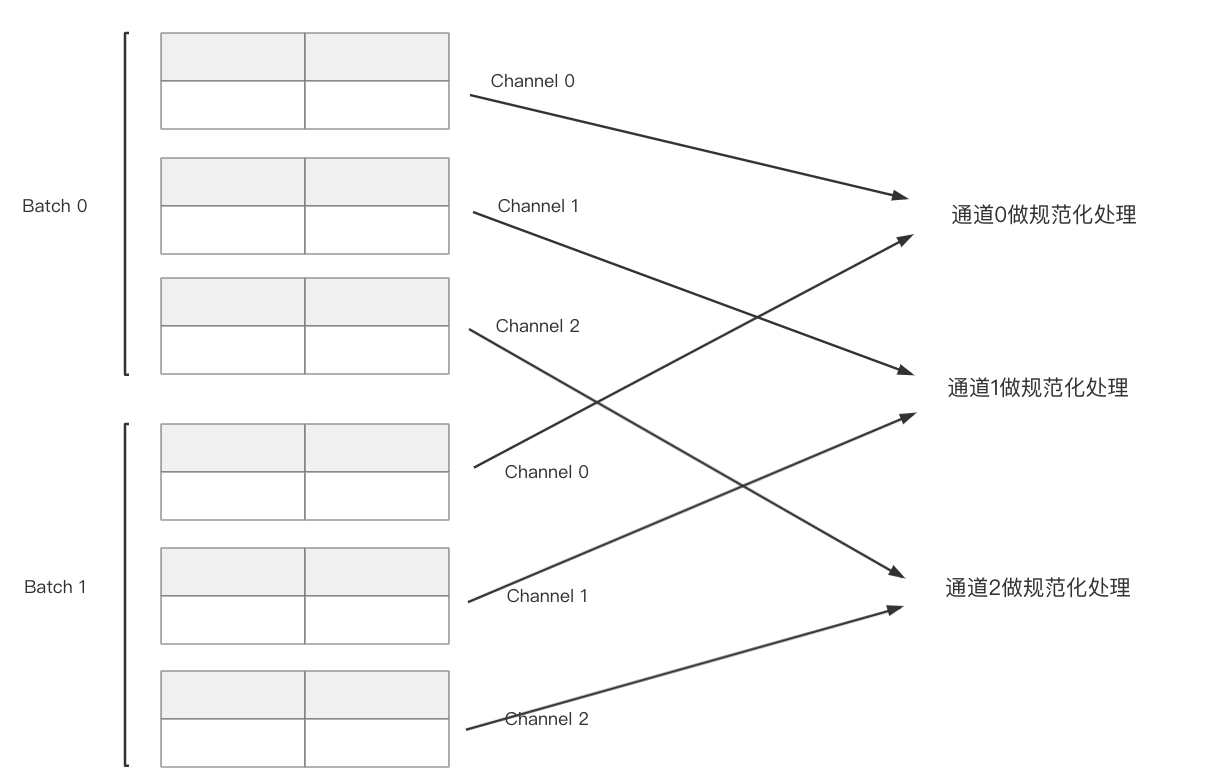
主要作用在特征上,比如输入维度为B*C*H*W, B代表batchsize大小,C代表channel,H代表图片的高度维度,W代表图片的宽度维度;
而nn.BatchNorm2d是对channel做归一化处理,也就是对批次内的特征进行归一化;
如输入B * C * H * W = (2 * 3 * 2 * 2):
计算的均值和方差的方式实际上是把batch内对应通道的数据拉平计算;
演示代码:
>>> y = torch.randn(2,3,2,2)
>>> y
tensor([[[[-0.3008, 0.7066],
[ 0.5374, -0.4211]],
[[-0.3935, 0.6193],
[ 0.5375, -0.2747]],
[[ 0.8895, 0.0956],
[-0.0622, 1.7511]]],
[[[-0.2402, 0.6884],
[ 0.5264, 0.3918]],
[[-0.3101, -0.6729],
[-0.5292, -1.0383]],
[[-0.6681, -0.3747],
[ 0.3431, 0.3245]]]])
>>> n = nn.BatchNorm2d(3)
>>> n.weight
Parameter containing:
tensor([1., 1., 1.], requires_grad=True)
>>> n.bias
Parameter containing:
tensor([0., 0., 0.], requires_grad=True)
>>> n(y)
tensor([[[[-1.2111, 1.0613],
[ 0.6797, -1.4823]],
[[-0.2544, 1.6433],
[ 1.4902, -0.0318]],
[[ 0.8494, -0.2705],
[-0.4931, 2.0649]]],
[[[-1.0742, 1.0204],
[ 0.6549, 0.3513]],
[[-0.0981, -0.7779],
[-0.5086, -1.4626]],
[[-1.3479, -0.9340],
[ 0.0786, 0.0524]]]], grad_fn=<NativeBatchNormBackward0>)
关于均值方差的计算方法演示:
>>> z = [-1.2111, 1.0613, 0.6797, -1.4823, -1.0742, 1.0204, 0.6549, 0.3513] # 每个通道拉平计算
>>> import numpy as np
>>> np.mean(z) # 10的-17次方就是0
-2.7755575615628914e-17
>>> np.std(z) # numpy默认是有偏的, torch的模式是无偏的
0.9999846111315913
参考:[pytorch 网络模型结构] 深入理解 nn.BatchNorm1d/2d 计算过程_哔哩哔哩_bilibili