论文地址:https://doi.org/10.1016/j.patcog.2021.107867
发表于:PR 2021
Abstract
显著目标检测(SOD)是计算机视觉领域的一个基本问题。本文提出了一个新颖的空间上下文感知网络(SCA-Net),用于图像中的SOD。与最近其他基于深度学习的SOD方法相比,SCA-Net能够更有效地聚合多级深度特征。一个长路径上下文模块(LPCM)用于赋予包含全局信息特征图更好的辨别能力。这样,就可以得到一个更好的初始saliency map,以用于后续的预测。此外,SCA-Net还采用了一个短路径上下文模块(SPCM),用于逐步加强局部上下文线索与全局特征之间的互动。在五个大型benchmark上进行的广泛实验表明,SCA-Net与最近的SOTA相比取得了良好的性能。
I. Motivation
在CNN中,全局上下文信息是通过一系列下采样操作(如不同stride卷积层、池化层)得到的。对于最终得到的全局特征,存在这么些问题:
- 空间分辨率较小
- 缺乏局部细节
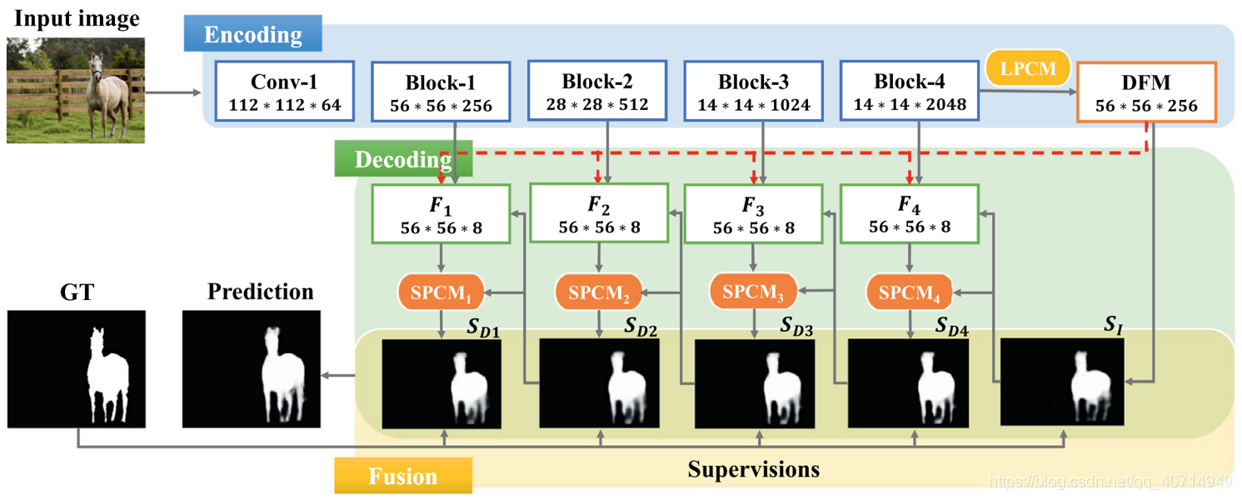
而后续的预测过程基本都是要基于Encoder学到的全局特征的,全局特征的质量会对最终结果产生关键的影响,一个例子如下所示:
一般来说,得到的全局特征图会像b这样,确实能够包含显著目标(图中的马)的大致位置,但是在一些关键区域(如耳朵、腿)仍然是模糊的。因此,有必要提升全局特征中这些模糊区域的可区分性,达到类似c中的效果。
此外,对于许多方法,局部上下文信息是通过将深层信息与浅层信息逐渐融合得到的,而如果此时中间特征包含大量噪声,便会影响最终特征融合的效果,如上图e所示。因此,需要寻找一种方法来恢复全局特征图中的细节信息。
II. Network Architecture
从整体结构而言,分为三个部分:Encoding Network(ResNet 50)、Decoding Network、Fusion Network。
III. Long-Path Context Module
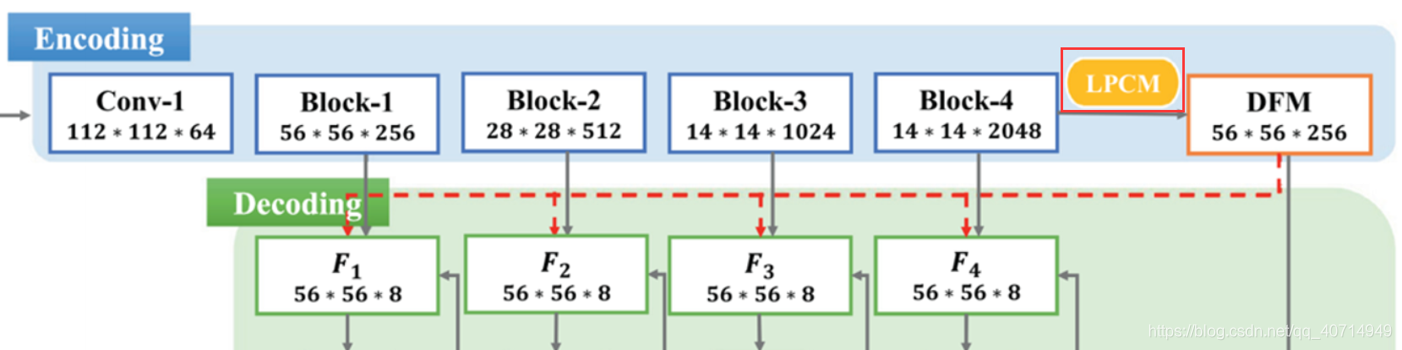
Long-Path Context Module,长路径上下文模块,这个东西的作用是"提升包含全局信息的特征图的可判别性",也就是对全局特征做文章,提升下全局特征的精度。既然是用来处理全局特征的,那么LPCM位置基本上就跑不了了,与大多数情况类似,其位于Encoder与Decoder的连接处:
因为文中没有给出LPCM的结构示意图,因此下面用公式一点一点来分析这个模块的思想和作用。
在此之前,需要先了解Affinity Matrix(亲和矩阵,相似矩阵)是什么东西。一般来说在计算机视觉任务中,Affinity Matrix算的就是图像中每个点与其他所有点的相关性,而这个相关性通常是用余弦相似度来计算的。当两个向量垂直时,cos值为0,不相似;当两个向量平行时,cos值为1,相似。低相关性意味着相应像素的独特性。有关Affinity Matrix的一些更详细的讲解可以见文章[1~2]。
记输入特征图为
F
∈
R
W
×
H
×
C
\mathbf{F} \in \mathbb{R}^{W \times H \times C}
F∈RW×H×C,
f
i
∈
R
1
×
1
×
C
\mathbf{f}_{i} \in \mathbb{R}^{1 \times 1 \times C}
fi∈R1×1×C为
F
\mathbf{F}
F于
(
W
i
,
H
i
)
\left(W_{i}, H_{i}\right)
(Wi,Hi)处的特征向量,
x
i
\mathbf{x}_{i}
xi、
x
j
\mathbf{x}_{j}
xj分别为
(
W
i
,
H
i
)
\left(W_{i}, H_{i}\right)
(Wi,Hi)、
(
W
j
,
H
j
)
\left(W_{j}, H_{j}\right)
(Wj,Hj)处的特征向量,
g
(
x
i
,
x
j
)
g\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)
g(xi,xj)为相关系数,计算的是
x
i
\mathbf{x}_{i}
xi、
x
j
\mathbf{x}_{j}
xj之间的相关性(即上文提到的亲和矩阵中的亲和性)。至此,可以将LPCM模块的任务记为下式:
f
i
L
=
1
N
(
x
)
∑
∀
j
g
(
x
i
,
x
j
)
⋅
f
j
\mathbf{f}_{i}^{L}=\frac{1}{\mathcal{N}(\mathbf{x})} \sum_{\forall j} g\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right) \cdot \mathbf{f}_{j}
fiL=N(x)1∀j∑g(xi,xj)⋅fj 即,将某个位置原有的特征向量
f
i
\mathbf{f}_{i}
fi,替换为了图像中其余位置所有特征向量的加权和
f
i
L
\mathbf{f}_{i}^{L}
fiL。上式中
N
(
x
)
\mathcal{N}(\mathbf{x})
N(x)为标准化因子,作用为保证相关系数的和1,有
1
N
(
x
)
∑
∀
j
g
(
x
i
,
x
j
)
=
1
\frac{1}{\mathcal{N}(\mathbf{x})} \sum_{\forall j} g\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=1
N(x)1∑∀jg(xi,xj)=1。和一般卷积操作相比,这相当于将感受野扩展到了整张特征图,对全局信息进行了编码。
落实到具体网络实现,首先,将特征图
F
\mathbf{F}
F按通道展开,得到
F
‾
∈
R
N
×
C
\overline{\mathbf{F}} \in \mathbb{R}^{N \times C}
F∈RN×C,其中
N
=
W
×
H
N=W \times H
N=W×H。那么上面刚提到的LPCM任务式便可以被重写为:
F
‾
L
=
G
L
×
F
‾
\overline{\mathbf{F}}^{L}=\mathbf{G}^{L} \times \overline{\mathbf{F}}
FL=GL×F 其中
G
L
=
{
g
(
x
i
,
x
j
)
}
i
,
j
=
1
N
∈
R
N
×
N
\mathbf{G}^{L}=\left\{g\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)\right\}_{i, j=1}^{N} \in \mathbb{R}^{N \times N}
GL={g(xi,xj)}i,j=1N∈RN×N便表示长路径亲和矩阵。在该矩阵中,每个元素都对成对的亲和关系进行了编码。可以看到,这其实就是个可微的线性变换,因此很容易使用CNN进行实现。落实到具体特征上,有:
f
j
=
f
(
x
j
)
=
W
f
x
j
\mathbf{f}_{j}=f\left(\mathbf{x}_{j}\right)=\mathbf{W}_{f} \mathbf{x}_{j}
fj=f(xj)=Wfxj
W
f
\mathbf{W}_{f}
Wf就是个可学习的权重矩阵。而对于相关性的具体计算,有:
g
(
x
i
,
x
j
)
=
e
α
(
x
i
)
T
β
(
x
j
)
g\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=e^{\alpha\left(\mathbf{x}_{i}\right)^{T} \beta\left(\mathbf{x}_{j}\right)}
g(xi,xj)=eα(xi)Tβ(xj) 其中
α
(
x
i
)
=
W
α
x
i
\alpha\left(\mathbf{x}_{i}\right)=\mathbf{W}_{\alpha} \mathbf{x}_{i}
α(xi)=Wαxi,
β
(
x
j
)
=
W
β
x
j
\beta\left(\mathbf{x}_{j}\right)=\mathbf{W}_{\beta} \mathbf{x}_{j}
β(xj)=Wβxj为嵌入函数。
总体看下来,命名中的Long-Path,其实对应的就是这个Affinity Matrix。由于亲和矩阵的计算需要与特征图中各位置的特征向量进行比较,所以其是"长路径"的。至于最终作用,LSPM可以利用相似性强化局部区域(前景),并弱化背景。
IV. Short-Path Context Module
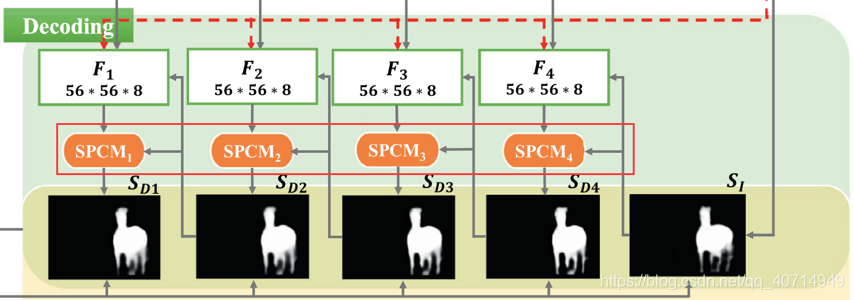
Short-Path Context Module,短路径上下文模块,这个东西的作用是"逐步加强局部上下文与全局特征之间的交流",也就是做局部特征与全局特征的融合。从这一作用的角度,容易想到其位于各Decoder的连接处:
相比于LPCM的一点在于这次SPCM是给出网络结构图了…不过我们依然先从数学推导开始说明。同样地,记输入特征图为
F
∈
R
W
×
H
×
C
\mathbf{F} \in \mathbb{R}^{W \times H \times C}
F∈RW×H×C,SPCM的目标是得到:
f
i
S
=
1
N
(
x
)
∑
j
∈
N
(
x
i
)
g
(
x
i
,
x
j
)
⋅
f
j
\mathbf{f}_{i}^{S}=\frac{1}{\mathcal{N}(\mathbf{x})} \sum_{j \in N\left(\mathbf{x}_{i}\right)} g\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right) \cdot \mathbf{f}_{j}
fiS=N(x)1j∈N(xi)∑g(xi,xj)⋅fj 这里与LPCM的一点不同是,
j
j
j不再是图中其他任意位置,而只是输入
x
i
\mathbf{x}_{i}
xi的附近位置(周围一圈八格),所以这个东西是"短路径"的。记此时的短路径亲和矩阵为
G
S
\mathbf{G}^{S}
GS,类似地,将
F
\mathbf{F}
F按通道展开,有:
F
‾
S
=
G
S
×
F
‾
\overline{\mathbf{F}}^{S}=\mathbf{G}^{S} \times \overline{\mathbf{F}}
FS=GS×F 作为一个矩阵乘法,其同样可以改写为下式以便用卷积网络实现:
f
i
,
j
S
=
∑
s
,
t
=
−
1
1
w
i
,
j
(
s
,
t
)
⊙
f
i
+
s
,
j
+
t
\mathbf{f}_{i, j}^{S}=\sum_{s, t=-1}^{1} \mathbf{w}_{i, j}(s, t) \odot \mathbf{f}_{i+s, j+t}
fi,jS=s,t=−1∑1wi,j(s,t)⊙fi+s,j+t
f
i
,
j
\mathbf{f}_{i, j}
fi,j为
(
i
,
j
)
(i,j)
(i,j)处的特征向量,
w
i
,
j
∈
R
3
×
3
×
C
\mathbf{w}_{i, j} \in \mathbb{R}^{3 \times 3 \times C}
wi,j∈R3×3×C为网络的可学习参数(即3×3卷积核),
⊙
\odot
⊙为element-wise乘。
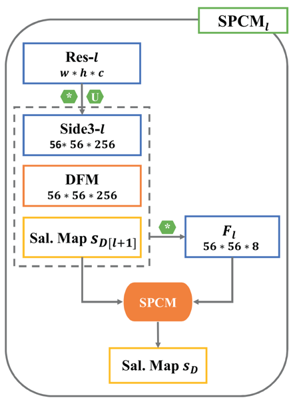
SPCM的结构示意图如下:
V. Fusion Network
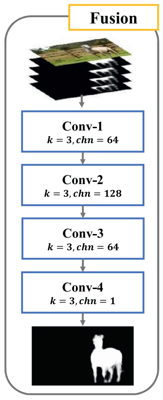
Fusion Network做的是side-output prediction的融合,以得到最终的预测结果。这里比较有意思的一点是,其将原始图像也引入了融合过程中,如下所示:
具体过程如下:
- 将各side-output prediction上采样至原图像尺寸
- 将采样后的各prediction与原始图像进行channel-wise concat
- 通过四个卷积层学习得到最终结果
VI. Loss
本文没有采用比较特别的loss设计技巧,还是用的Cross Entropy交叉熵损失,最终的loss如下:
L
total
=
L
I
+
∑
i
=
1
4
L
D
(
i
)
+
L
F
\mathcal{L}_{\text {total }}=\mathcal{L}_{I}+\sum_{i=1}^{4} \mathcal{L}_{D}^{(i)}+\mathcal{L}_{F}
Ltotal =LI+i=1∑4LD(i)+LF
其中:
- L I \mathcal{L}_{I} LI: 初始预测结果 S I \mathbf{S}_{I} SI的损失
- L D ( i ) \mathcal{L}_{D}^{(i)} LD(i): 中间预测结果 S D i \mathbf{S}_{Di} SDi的损失
- L F \mathcal{L}_{F} LF: 最终预测结果 S F \mathbf{S}_{F} SF的损失
VII. Experiment
性能超越了13个最近模型,包括MINet(CVPR 2020)、RAS(ECCV 2018)、PoolNet(CVPR 2019)、AFNet(CVPR 2019)、BAS(CVPR 2019)、HRSD(ICCV 2019)、MLMS(CVPR 2019)、PiCA(CVPR 2018)、BMPM(CVPR 2018)、PAGR(CVPR 2018)、R3Net(IJCAI 2018)、Amulet(ICCV 2017)、DSS(CVPR 2017)
VIII. Summary
从出发点来讲,本文做的是比较经典的如何处理Encoder得到的全局特征(LPCM)与怎样进行更好的特征融合(SPCM),核心创新思想在于引入了在传统图像领域里面用的更多一些的Affinity Matrix概念,用来强化模型去学习"对比度"这样的一个能力。
Ref
[1] https://blog.csdn.net/haohulala/article/details/109602671
[2] https://deepai.org/machine-learning-glossary-and-terms/affinity-matrix