给你一个整数数组 colors 和一个整数 k ，colors表示一个由红色和蓝色瓷砖组成的环，第 i 块瓷砖的颜色为 colors[i] ：

• colors[i] == 0 表示第 i 块瓷砖的颜色是 红色 。
• colors[i] == 1 表示第 i 块瓷砖的颜色是 蓝色 。

环中连续 k 块瓷砖的颜色如果是 交替 颜色（也就是说除了第一块和最后一块瓷砖以外，中间瓷砖的颜色与它 左边 和 右边 的颜色都不同），那么它被称为一个 交替 组。

请你返回 交替 组的数目。

注意 ，由于 colors 表示一个 环 ，第一块 瓷砖和 最后一块 瓷砖是相邻的。

示例 1：

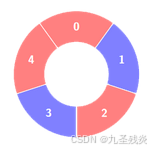
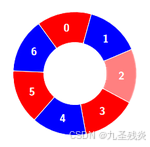
输入：colors = [0,1,0,1,0], k = 3

输出：3

解释：

交替组包括：

示例 2：

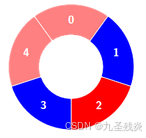
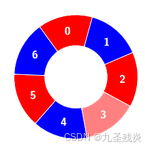
输入：colors = [0,1,0,0,1,0,1], k = 6

输出：2

解释：

交替组包括：

示例 3：

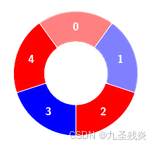
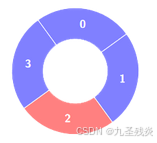
输入：colors = [1,1,0,1], k = 4

输出：0

解释：

提示：

• 3 <= colors.length <= 10^5
• 0 <= colors[i] <= 1
• 3 <= k <= colors.length

我的解答：

class Solution {
    public int numberOfAlternatingGroups(int[] colors, int k) {
        int size = colors.length;
        int res = 0;
        int[] new_colors = new int[2 * size];
        int new_size = new_colors.length;
        for(int i = 1; i < new_size; i++){
            int p = (i - 1) % size;
            int l = i % size;
            if(colors[p] != colors[l]){
                new_colors[i] = new_colors[i - 1] + 1;
                // 如果元素在拓展位置且所在交替组的长度大于k，则说明以该元素为终点的交替组满足条件
                if(i >= size && new_colors[i] >= k - 1) res++;
            }
        }
        return res;
    }
}

优化

class Solution {
    public int numberOfAlternatingGroups(int[] colors, int k) {
        int size = colors.length - 1;
        int res = 0;
        int first_len = -1; // 记录从0开始的首个交替组长度
        int current_len = 1; // 以当前元素为终点的交替组的长度
        for(int i = 1; i <= size; i++){
            // 如果当前元素与上一元素相同，则表示交替组中断
            if(colors[i] == colors[i-1]){
                if(first_len == -1){
                    // 更新首个交替组
                    first_len = current_len;
                }else{
                    // 上一交替组中满足条件的组数
                    res += Math.max(0,current_len - k + 1);
                }
                current_len = 1;
            }
            else{
                current_len++;
            }
        }
        if(colors[0] != colors[size]){
            // 如果以尾元素为终点的交替组长度大于等于圆的长度，那么说明整个圆是循环交替的
            if(current_len > size) return size + 1;
            res +=  Math.max(0,(current_len + first_len - k + 1));
        }else{
            res +=  Math.max(0,(current_len - k + 1)) + Math.max(0,(first_len - k + 1));
        }
        return res;
    }
}