题目描述
最基本的01背包问题描述如下:
有
N
N
N件物品和一个容量为
V
V
V的背包,放入第
i
i
i个物品需要耗费的代价为
C
i
C_{i}
Ci,得到的价值为
W
i
W_{i}
Wi,求解将哪些物品装入背包可使价值总和最大。
解法
基本思路
最基础的背包问题,其每一件物品只有一个,可以选择放或者不放。一般采用二维动态规划来解决问题,通常定义其子状态为
d
p
[
i
]
[
v
]
dp[i][v]
dp[i][v],表示前
i
i
i个物品放入到容量为
v
v
v的背包中的最大的价值总和。那么这个值是如何得到的呢,对于第
i
i
i个物品,无非就是两种情况,放或者不放。如果不放或者根本放不下(
v
<
C
i
v < C_{i}
v<Ci),那么问题等同于前
i
−
1
i - 1
i−1个物品放入到容量为
v
v
v的背包的情况,即:
d
p
[
i
]
[
v
]
=
d
p
[
i
−
1
]
[
v
]
dp[i][v] = dp[i - 1][v]
dp[i][v]=dp[i−1][v]
如果选择放,那么问题就等同于前
i
−
1
i - 1
i−1个物品放入到容量为
v
−
C
i
v - C_{i}
v−Ci的背包的情况,即:
d
p
[
i
]
[
v
]
=
d
p
[
i
−
1
]
[
v
−
C
i
]
+
w
i
dp[i][v] = dp[i - 1][v - C_{i}] + w_i
dp[i][v]=dp[i−1][v−Ci]+wi
最终
d
p
[
i
]
[
v
]
dp[i][v]
dp[i][v]的取值就两者中更大的一个。
初始化dp数组时的细节
在大多数动态规划解法的题目中,初始化一直是很重要并且较难思考的一件事情。一般在求最优解的背包问题中,有两种问法,一个是要求“恰好装满背包”时的最优解,另一个则是不需要恰好装满背包,只求最优解。
如果是第一种情况,要求恰好装满背包,那么在初始化的时候,除了
d
p
[
0
]
[
0
]
dp[0][0]
dp[0][0]为0,其它的
d
p
[
0
]
[
1...
V
]
dp[0][1...V]
dp[0][1...V]均设为
−
∞
-\infty
−∞。说明此时只有容量为0的背包可以在什么也不装的情况下被“恰好装满”,其价值为0,而容量为1…V的背包,无法在没有物品的情况下被装满,没有合法的解,所以设定为
−
∞
-\infty
−∞。
对于第二种情况,题目并没有要求背包装满,只是希望价值尽可能大,那么
d
p
[
0
]
[
0...
V
]
dp[0][0...V]
dp[0][0...V]均初始化为0。因为任何容量的背包都有一个合法解“什么都不装”,这个解的价值为0,所以初始化状态的值也就全部为0了。
背包问题的优化
上述的基本思路中,时间和空间的复杂度均为
O
(
V
N
)
O(VN)
O(VN),其中的空间复杂度是可以被优化到
O
(
V
)
O(V)
O(V)的。从
d
p
[
i
]
[
v
]
dp[i][v]
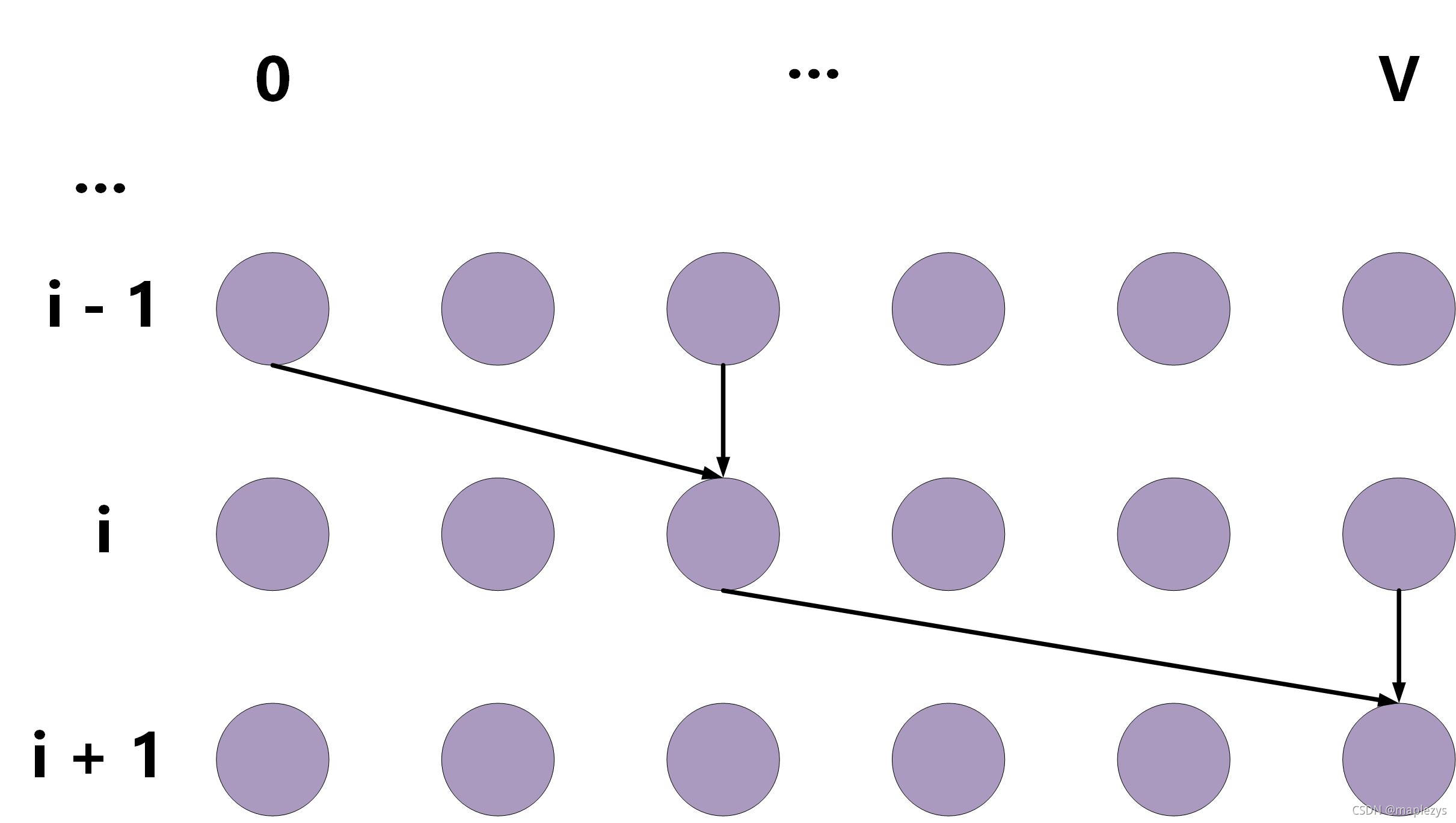
dp[i][v]的更新方程中不难看出,其实
d
p
[
i
]
dp[i]
dp[i]的值,只和
d
p
[
i
−
1
]
dp[i - 1]
dp[i−1]有关,如下图:
那我们在一开始初始化的时候,只需要初始化
d
p
[
0...
V
]
dp[0...V]
dp[0...V]大小的数组即可,每一次对物品的循环(
i
i
i)都只需要更新这一行数组就行。但需要注意的是,更新的时候要逆序更新,即从V更新到0。
举个例子,假如正向更新,访问到了
v
=
6
v=6
v=6的时候,你需要通过
n
e
w
_
d
p
[
6
]
=
m
a
x
(
o
l
d
_
d
p
[
6
]
,
o
l
d
_
d
p
[
3
]
)
new\_dp[6] = max(old\_dp[6], old\_dp[3])
new_dp[6]=max(old_dp[6],old_dp[3]),而由于是正向更新,
v
=
3
v=3
v=3的值已经被更新成了
n
e
w
_
d
p
[
3
]
new\_dp[3]
new_dp[3],
o
l
d
_
d
p
[
3
]
old\_dp[3]
old_dp[3]已经无法被访问,所以无法更新,所以这一层循环需要你需更新。
题目列表
在这里列举leetcode上四题经典01背包的题目。
416 分割等和子集
这题要求判断是否一个数组分成相等的两个子数组。
即选取若干个数字,刚好值为和的一半。
Python代码如下:
class Solution:
def canPartition(self, nums: List[int]) -> bool:
n = len(nums)
if n == 1: return False
total = sum(nums)
if total % 2 == 1: return False
target = total // 2
maxnum = max(nums)
if maxnum > target: return False
dp = [[False] * (target + 1) for _ in range(n)]
for i in range(n):
dp[i][0] = True
dp[0][nums[0]] = True
for i in range(1, n):
num = nums[i]
for j in range(1, target + 1):
if j < num:
dp[i][j] = dp[i - 1][j]
else:
dp[i][j] = dp[i - 1][j] | dp[i - 1][j - num]
return dp[n - 1][target]
优化空间复杂度的版本如下:
class Solution:
def canPartition(self, nums: List[int]) -> bool:
n = len(nums)
if n < 2:
return False
total = sum(nums)
if total % 2 != 0:
return False
target = total // 2
dp = [True] + [False] * target
for i, num in enumerate(nums):
for j in range(target, num - 1, -1):
dp[j] |= dp[j - num]
return dp[target]
474 一和零
原题连接
这题要求给你一个字符串数组,里面的字符串均为0和1组成,例如:strs = [“10”, “0001”, “111001”, “1”, “0”],再给你
m
=
5
m=5
m=5和
n
=
3
n=3
n=3,让你找出0的个数小于
m
m
m且1的个数小于
n
n
n的最大子集的长度。
这题同经典背包问题不同的是,它有两重限制,需要采用三维动态规划完成,Python代码如下:
class Solution:
def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
k = len(strs)
if m == 0 and n == 0: return 0
dp = [[[False] * (n + 1) for _ in range(m + 1)] for __ in range(k + 1)]
for s in range(k+1):
dp[s][0][0] = 0
for i in range(m+1):
for j in range(n+1):
dp[0][i][j] = 0
for s in range(1, k+1):
for i in range(m + 1):
for j in range(n + 1):
nums0, nums1 = self.count(strs[s - 1])
if nums0 <= i and nums1 <= j:
dp[s][i][j] = max(dp[s - 1][i][j], dp[s - 1][i - nums0][j - nums1] + 1)
else:
dp[s][i][j] = dp[s - 1][i][j]
return dp[k][i][j]
def count(self, s):
count0, count1 = 0, 0
for ss in s:
if ss == '0':
count0 += 1
elif ss == '1':
count1 += 1
return count0, count1
虽然是三维动态规划,但其也可以进行空间复杂度的优化,其代码如下:
class Solution:
def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
k = len(strs)
if m == 0 and n == 0: return 0
dp = [[0] * (n + 1) for _ in range(m + 1)]
dp[0][0] = 0
for s in range(1, k + 1):
for i in range(m, -1, -1):
for j in range(n, -1, -1):
nums0, nums1 = self.count(strs[s - 1])
if nums0 <= i and nums1 <= j:
dp[i][j] = max(dp[i][j], dp[i - nums0][j - nums1] + 1)
return dp[m][n]
def count(self, s):
count0, count1 = 0, 0
for ss in s:
if ss == '0':
count0 += 1
elif ss == '1':
count1 += 1
return count0, count1
494 目标和
原题连接
题目要求,将给的数组中每个数字前面添加“
+
+
+”或者“
−
-
−”,使得整个公式的和为题目给的target,问一共有多少种公式。
例如,对于nums = [1,1,1,1,1], target = 3,则共有5种公式:
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
第一眼看上去这题与背包问题并不一致,需要做一点小小的改变。通过所有数的总和以及给出的target,我们可以计算出所有前面符号为“
−
-
−”的数的总和为
t
o
t
a
l
−
t
a
r
g
e
t
2
\frac{total - target}{2}
2total−target。原题也就转换成,要求出有多少种挑选的方法可以使得挑选出来的数字和为
t
o
t
a
l
−
t
a
r
g
e
t
2
\frac{total - target}{2}
2total−target,和416类似。此外,若
t
o
t
a
l
−
t
a
r
g
e
t
2
\frac{total - target}{2}
2total−target根本就只是小数,那说明一种方法都没有,直接返回0。
Python代码如下:
class Solution:
def findTargetSumWays(self, nums: List[int], target: int) -> int:
total = sum(nums)
if total < target: return 0
if (total - target) % 2 == 1: return 0
neg = (total - target) // 2
n = len(nums)
dp = [[0] * (neg + 1) for _ in range(n + 1)]
dp[0][0] = 1
for i in range(1, n + 1):
for j in range(neg + 1):
if nums[i - 1] > j:
dp[i][j] = dp[i - 1][j]
else:
dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i - 1]]
return dp[n][neg]
优化版本的Python代码如下:
class Solution:
def findTargetSumWays(self, nums: List[int], target: int) -> int:
total = sum(nums)
if total < target: return 0
if (total - target) % 2 == 1: return 0
neg = (total - target) // 2
n = len(nums)
dp = [0] * (neg + 1)
dp[0] = 1
for i in range(1, n + 1):
for j in range(neg, -1, -1):
if nums[i - 1] <= j:
dp[j] += dp[j - nums[i - 1]]
return dp[-1]
879 目标和
原题连接
原题看上去比较复杂,其实跟474一样,是二重限制的背包问题,需要三重动态规划来解。
Python代码如下:
class Solution:
def profitableSchemes(self, n: int, minProfit: int, group: List[int], profit: List[int]) -> int:
length = len(group)
dp = [[[0] * (minProfit + 1) for _ in range(n + 1)] for _ in range(length + 1)]
dp[0][0][0] = 1
for i in range(1, length + 1):
g, p = group[i - 1], profit[i - 1]
for j in range(n + 1):
for k in range(minProfit + 1):
if j < g:
dp[i][j][k] = dp[i - 1][j][k]
else:
dp[i][j][k] = (dp[i - 1][j][k] + dp[i - 1][j - g][max(0, k - p)]) % (10**9 + 7)
ans = sum(dp[length][j][minProfit] for j in range(n + 1))
return ans % (10**9 + 7)
其中,在状态转移的时候,
d
p
[
k
]
dp[k]
dp[k]并不是直接等于
d
p
[
k
−
p
r
o
f
i
t
[
i
−
1
]
]
dp[k - profit[i - 1]]
dp[k−profit[i−1]],这是因为
k
k
k代表着至少利润是
k
k
k,
k
−
p
r
o
f
i
t
[
i
−
1
]
k - profit[i - 1]
k−profit[i−1]是可能为负的,也是合法状态,但数组中并没有存储“利润至少为负”的状态,所以需要改成
d
p
[
m
a
x
(
0
,
k
−
p
r
o
f
i
t
[
i
−
1
]
)
]
dp[max(0, k - profit[i - 1])]
dp[max(0,k−profit[i−1])],因为“利润至少为负”和“利润至少为零”是等价的。
优化版本的Python代码如下:
class Solution:
def profitableSchemes(self, n: int, minProfit: int, group: List[int], profit: List[int]) -> int:
dp = [[0] * (minProfit + 1) for _ in range(n + 1)]
for i in range(0, n + 1):
dp[i][0] = 1
for earn, members in zip(profit, group):
for j in range(n, members - 1, -1):
for k in range(minProfit, -1, -1):
dp[j][k] = (dp[j][k] + dp[j - members][max(0, k - earn)]) % (10**9 + 7)
return dp[n][minProfit]