前言

  trie 是专门为处理字符串而设计的。

  假设一下，如果有 n 个条目，使用树结构，那么查询的时间复杂度为 O(logn)。如果有 100 万个条目，logn 大约有 20。但是如果我们使用 trie，它的查询的时间复杂度和字典中一共多少个条目无关。只与查询的字符串的长度相关，若要查询的字符串长度为 w，那么时间复杂度为 O(w)。这是非常有优势的，因为对于绝大多数的单词而言，长度一般小于 10。

  下面，我们来看一下，trie 是怎么实现的。

什么是 Trie？

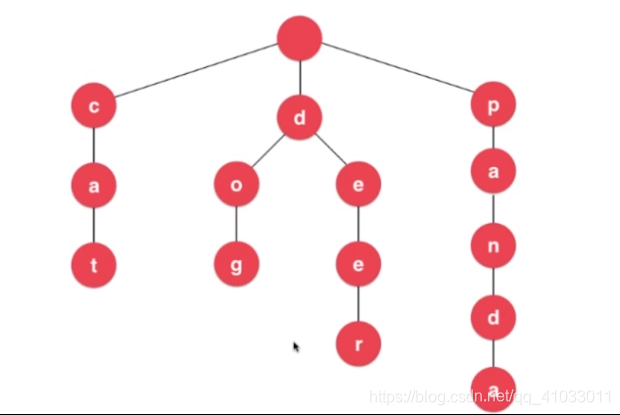
下图是 Trie 的图形结构

  Trie 是以字母为单位，将每个字符串拆开存储，每个节点有 26 个指向下个节点的指针。所以每个节点大概有以下定义：

class Node{
	char c;			// 每个节点表示的字母
	Node next[26];	// 每个节点的有26个指向下个节点的指针
};

  这里会有一个问题，就是我们指定了每个节点后只有 26 个指向下一节点的指针，那么就限制了 trie 的功能，只能统计英文小写字母，如果考虑到大小写，那么每个节点后面应该有 52 个指针。但是如果存储网址等信息，那么包含的信息更多，比如 @，/，_等等，所以我们最好不要将 next 固定。最后我们考虑用一个 map 来实现 next。定义如下：

class Node{
	char c;
	map<char, Node> next;
};

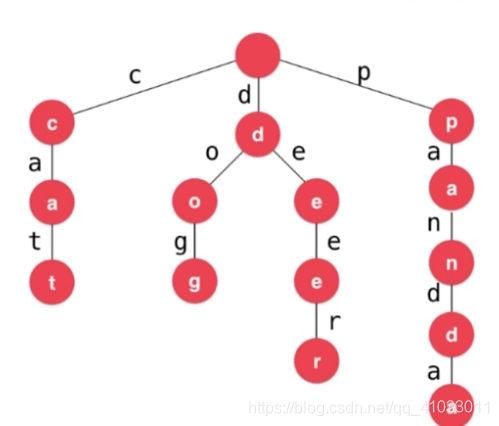
  下面，我们再来看另外一个问题。上面在绘制 Trie 的时候，在每个节点上都填充了一个字母，但是，可以想象一下，我们从根节点找到下一个节点的过程中，我们已经知道这个字母是谁了。比如，我们要在下图搜索 cat 这个单词，我们之所以能来到 c 这个节点，是因为我们知道了下一个节点是要到 c 这个字母所在的节点。所以，其实更准确的来讲，我们应该把这个字母标在这个边上，那么，在节点的数据结构中，我不存储每个节点所对应的字母是没有问题的。

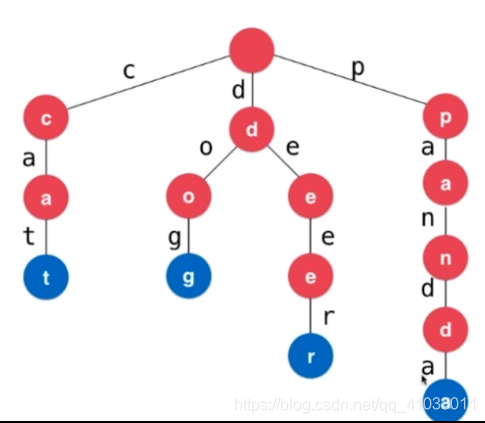
  从根节点出发，一直到叶子节点，说明查询到了一个单词。比如下图，我们遍历到了 t 这个节点，说明查询到了 cat 这个单词；遍历到了 g 这个节点，说明查询到了 dog 这个单词。我们依次把这些叶子节点做相应的标记。

  在我们的英语单词世界中，很多单词可能是另一种单词的前缀。比如 pan(平底锅) 就是 panda(熊猫) 这个单词的前缀。所以，我们 p - a - n - d - a 这条路径中，我们既要存储 pan 这个单词，也要存储 panda 这个单词。所以，我们对于每一个 Node，都需要一个标识，这个标识来告诉大家，当前这个节点是否是某一个单词的结尾，某一个单词的结尾只靠叶子节点是不能区别出来的。

  所以，Node 节点中应该增添一个 bool 类型的数据结构，表示该节点是否是某个单词的结尾。

class Node{
	bool isWord;
	map<char, Node> next;
};

下面我们开始书写代码：

  首先定义一个 Trie 类，里面包含一个节点类

class Trie
{
private:
    class Node{		// 节点类
    public:
        bool isWord;
        map<char, Node*> next;
         Node()
        {
            this->isWord = false;
        }
        Node(bool isWord){
            this->isWord  = isWord;
        }
    };

    Node *root;      // 根节点
    long long size;       // Trie 存储的单词个数
    public:
        Trie()
        {
            root = new Node();
            size = 0;
        }
        ~Trie()
        {
            delete root;
        }
};

向 Trie 中添加新单词 word

		void add(string word)
        {
            Node *cur = root;		
            for(int i = 0; i < word.size(); i++)
            {
                char c = word[i];
                // 检查 c 存不存在
                if(cur->next[c] == nullptr)		// 如果节点不存在，就创建一个新结点
                    cur->next[c] = new Node();
                cur = cur->next[c];				// cur 指向下一个节点
            }
            if(!cur->isWord){		// 判断单词在 Trie 中是否已经存在，若已经存在，直接返回，不存在，改变其 isWord 的值，并将 size++
                cur->isWord = true;
                size++;
            }
        }

查询某个单词是否在 Trie 中

		bool contains(string word)
        {
            if(size == 0)		// 如果 Trie 中没有单词，直接返回
                return false;
            Node *cur = root;
            for(int i = 0; i < word.size(); i++)
            {
                char c = word[i];
                if(cur->next[c])
                    cur = cur->next[c];
                else
                    return false;
            }
            return cur->isWord;
        }

  到此，我们实现了 Trie 的两个基本功能，插入和查找，让我们实现一下 Trie 的功能吧！

  下面我将一个文本中的单词保存到一个字符串数组中，然后插入到 Trie 上，然后再在 Trie 中查找这些单词，统计所需时间。下面请看示例代码：

#include <iostream>
#include <fstream>
#include <vector>
#include <ctime>
#include "Trie.h"
using namespace std;
// 判断一个字符串是不是英文字符串
bool isword(const string &str)
{
    if(str[0] >= '1' && str[0] <= '9')
        return false;
    for(char c : str)
    {
        if(!( (c >= 'a' && c <= 'z') || (c >= 'A' && c <= 'Z')))
            return false;
    }
    return true;
}
//去掉英文字符串结尾的标点符号
void subString(string &str)
{
    char c = str[str.length() - 1];
    if(!( (c >= 'a' && c <= 'z') || (c >= 'A' && c <= 'Z')) )
        str = str.substr(0, str.size() - 2);
 }
void Test1()
{
    Trie t;
    ifstream readFile("D://test.txt");
    string s;
    vector<string> words;
    while(!readFile.eof())
    {
        readFile >> s;
        if(isword(s))
        {
            subString(s);
            words.push_back(s);
        }
    }
    clock_t startTime = clock();
    for(string w : words)
        t.add(w);			// 将单词添加到 trie 中
    for(string w : words)
        t.contains(w);		// 在 Trie 中查找这些单词
    clock_t endTime = clock();
    cout << "Total different words：" <<  t.getSize() << endl;
    cout << "Trie：" << double(endTime - startTime) / CLOCKS_PER_SEC << " s " << endl;


}
int main()
{
    Test1();
    return 0;
}

运行结果如下：

Trie 和 前缀搜索

代码如下：

  		// 查询是否在 Trie 中有单词以 prefix 为前缀
        bool isPrefix(string prefix)
        {
            if(size == 0)
                return false;
            Node *cur = root;
            for(int i = 0; i < prefix.size(); i++)
            {
                char c = prefix[i];
                if(cur->next[c])
                    cur = cur->next[c];
                else
                    return false;
            }
            return true;    //只要存在 prefix 这个节点，那么就肯定有以它为前缀的单词
        }

Trie 的局限性

最大的问题：空间！

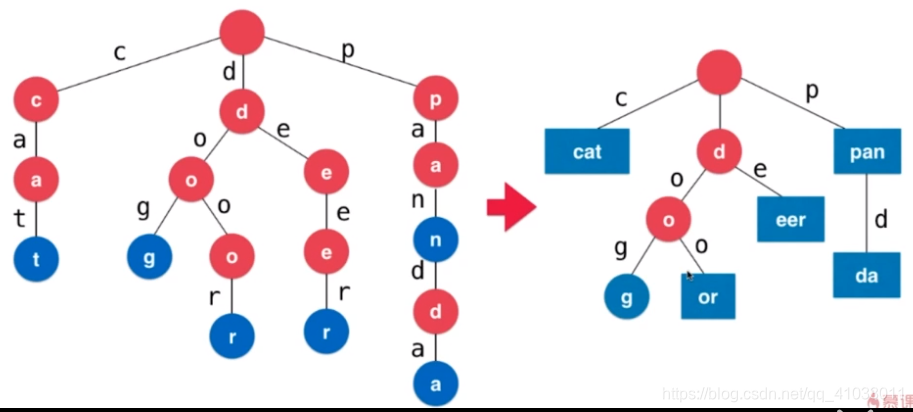
  其实对于每一个 Node，它只承载了一个字符的信息，而对于从这个字符到下一个字符，需要使用 map 来映射到下一个字符。即使我们讨论的是 26 个字母表这样一个字符空间的话，这个 map 最终也要存储 26 条记录，换句话说，我们的存储空间整体基本可以认为是原来的字符串所占空间的 27 倍。那么这个空间的消耗是极其大的。为了解决这个问题，相应的，也有一些变种，最为典型的一种变种是 压缩字典树（Compressed Trie）。如下图所示：

  什么是压缩字典树呢？从上图可以看出，很多字符后面都是单链的形式，比如 cat，c 字符后面只有 a，a 字符后面只有 t。那么我们可不可以把它们进行压缩一下呢？答案是可以的，因为从 c 字符开始。后面只有 a 字符，那么一个 Trie 就被改造成如下形式：

  这样的一棵树就被称为 压缩字典树。可以看出，它的空间节省了一部分，它的缺点就是维护成本更高了。如果我们向压缩字典树中添加一个单词，比如 ：park，从根节点出发经过 p，pa 是 pan 的前缀，所以我们需要 pan 先拆成 pa 和 n 两部分，再将 park 这个单词加进去，所以整体部分更加复杂一些。

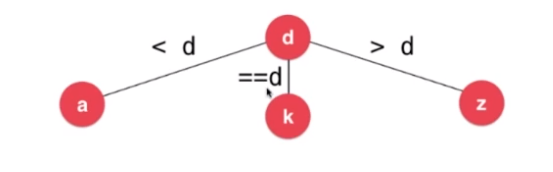
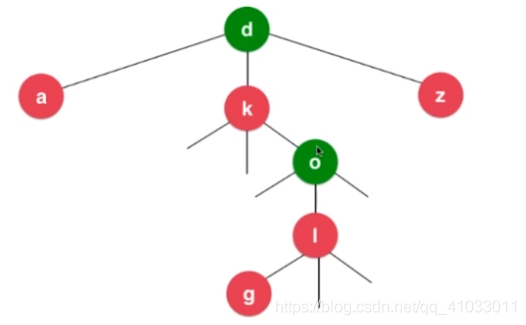
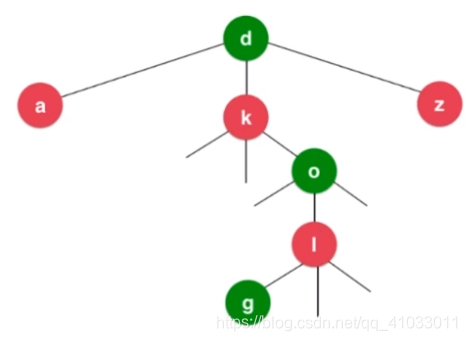
  另外一种改造方式，其实也是一种很经典的数据结构，三分搜索树（Ternary Search Trie）。下图是三分搜索树的图示。

  对于任意一个节点 d，这三个分支分别代表小于 d，等于 d 和大于 d 三部分。

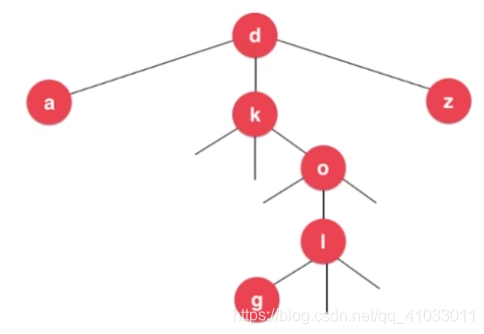
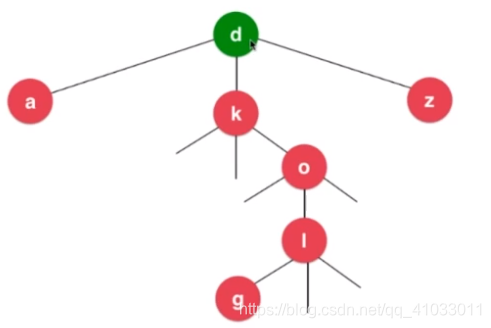
  其实上图的三分搜索树中存储了 dog 这个词，可能有些朋友看得不是很清楚。下面讲解一下搜索 dog 这个单词的过程。

  首先搜索字母 d，这个根节点就是 d，那么我们找到根节点。

  之后，我们就可以直接看 d 中间这个分支的下一个节点。下一个节点是 k，但是我们要找的下一个字母是 o，o 在字母表中位于 k 之后，所以我们往 k 节点的右分支找。k 的右分支的下一个节点是 o，然后我们就找到了字母 o。

  相应的，我们继续到 o 的中间这个分支继续找，o 的下一个节点是 l，g 比 l 小，所以到 l 的左分支的下一个节点找，我们成功找到了 g。到此，寻找 dog 这个单词完成。

  由此可见，我们使用三分搜索树查找单词所需要的次数有可能是要比单词长度要多的，因为我们会遍历一些其它的字符。不过它的优点是对于每一个节点，它只有左中右三个孩子，而不像 Trie 那样，用一个 map 来表示它的孩子。大大节省了空间，相应的也是牺牲了一点点时间。

  Trie 是一种前缀树，相应的，也有一种后缀树。后缀树在解决很多模式匹配的问题的时候，都有非常大的优势。

  这里有更多关于字符串的问题：比如子串查询，可以使用 KMP，Boyer-Moore，Rabin-Karp。还有一个更重要的问题：文件压缩。比如：哈夫曼算法。另外还有一种是 模式匹配，这也是讨论字符串相关的问题。