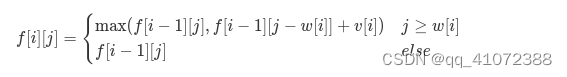题目：现在有四个物品，背包总容量为8，背包最多能装入价值为多少的物品？

物品编号 1 2 3 4
物品体积 2 3 4 5
物品价值 3 4 5 6

解法：
一、如果装不下当前物品，那么前n个物品的最佳组合和前n-1个物品的最佳组合是一样的。
二、如果装得下当前物品
假设1：装当前物品，在给当前物品预留了相应空间的情况下，前n-1个物品的最佳组合+当前物品的价值就是总价值。
假设2：不装当前物品，前n个物品的最佳组合和前n-1个物品的最佳组合是一样的。
选取假设1和假设2中较大的价值，为当前最佳组合的价值

升级：在使得背包内总价值最大的情况下，背包内装了哪些物品？
解法：从表的右下角开始回溯，如果发现前n个物品的最佳组合和前n-1个物品的最佳组合一样，说明第n个物品没有被装入；否则，第n个物品被装入

/*
v：物品种类数量
w[]：重量数组
v[]：价值数组
c：背包总容量
int[] object = new int[v]：存放的哪些物品
*/
void dynamic() {
   	//动态规划找到其下最大价值
	for(int i = 1; i <= v; i++){
   
		for(int j = 1; i <= c; j++){
   
			if(w[i] > j)
				dp[i][j] = dp[i-1][j];
			else
				dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-w[i]]+v[i]);
		}
	}
}

void Find(int i, int j) {
   	//回溯找到背包内价值最大时，有哪些物品
	if(i == 0) {
   
		for(int j = 0; j < v; j++)
			System.out.println(object[i]);//i表示物品编号；object[i]表示背包内是否有该物品
		return;
	}
	if(dp[i][j] = dp[i-1][j]) {
   
		object[i] = 0;
		Find(i-1, j);
	}
	else if(dp[i][j] == dp[i-1][j], dp[i-1][j-w[i]]+v[i]) {
   
		object[i] = 1;
		Find(i-1, j-w[i]);
	}
}

更新：

这是一道经典的动态规划问题，解题思路和上面背包问题思路一样
我们定义动规数组f[i][j]来表示前i件物品，容量为j时的最大价值，则

在本题中进行了一项变动，即物品分为主件和附件，考虑到一个主件最多可以购买两个附件，那我们可以细化分析，将是否购买该物品，细化为是否购买该物品，以及是否购买该物品的附件，即5种情况，不购买该物品，购买该物品，购买该物品及附件1，购买该物品及附件2，购买该物品及附件1及附件2，f[i][j]取这五种情况的最大值，这五种情况分别对应于

f[i−1][j]f[i-1][j]f[i−1][j]，

f[i−1][j−w[i]]+v[i]f[i-1][j-w[i]]+v[i]f[i−1][j−w[i]]+v[i]，

f[i][j]=max(f[i−1][j],f[i−1][j−w[i]−w[a1]]+v[i]+v[a1])f[i][j]=max(f[i-1][j], f[i-1][j-w[i]-w[a_1]]+v[i]+v[a_1])f[i][j]=max(f[i−1][j],f[i−1][j−w[i]−w[a1​]]+v[i]+v[a1​])，

f[i][j]=max(f[i−1][j],f[i−1][j−w[i]−w[a2]]+v[i]+v[a2])f[i][j]=max(f[i-1][j], f[i-1][j-w[i]-w[a_2]]+v[i]+v[a_2])f[i][j]=max(f[i−1][j],f[i−1][j−w[i]−w[a2​]]+v[i]+v[a2​])，

f[i][j]=max(f[i−1][j],f[i−1][j−w[i]−w[a1]−w[a2]]+v[i]+v[a1]+v[a2])f[i][j]=max