【论文地址】A-color-image-encryption-technique-using-exclusive-OR-with-DNA-complementary-rules-based-on-chaos-theory-and-SHA-2
使用基于混沌理论和SHA-2的异或与DNA互补规则的彩色图像加密技术
摘要
本研究使用SHA-256哈希函数修改混沌系统的初始条件和控制参数,将彩色图像的三个通道排列成一维矢量,并根据分段线性混沌映射产生的混沌序列进行排序。然后这个排列阵列被分成三个部分,每个部分代表一个颜色通道,并再次使用洛伦兹的混沌系统独立排列。该算法的新颖之处在于,通道的每个像素都被DNA互补规则的异或操作所取代。多重DNA规则被用来在一个序列中重复这个操作到一些随机的次数。这个操作迭代循环进行。这种循环操作开始的DNA选择规则和操作的延续依赖于Chen的混沌序列。大量的模拟实验结果表明,该算法仅在一次加密中就获得了良好的加密效果。
引言
如今,人们可以通过网络方便地传输各种多媒体信息。数字图像是多媒体通信的重要信息载体,如何保护图像信息是人们高度关注的问题,传统的分组加密方法(如DES、IDEA和AES)适用于图像加密,但对图像在传输过程中可能产生的传输噪声没有抵抗能力。因此,迫切需要研究新的图像加密算法。
由于数字图像在空间域中具有体积大、相关性强等固有特征,需要有一个独特的伪随机数生成器。混沌系统是一种很好的伪随机数生成器,因为它对种子和控制参数具有很高敏感性,而且计算量小,这标志着系统的有效性。
本文提出了一种新的彩色图像加密算法。利用SHA-256哈希函数修改PWLCM、Lorenz和Chen的混沌系统的初始条件和控制参数,以避免选择性明文攻击。为了打破彩色图像通道间的相关性,设计了双重置换。将红、绿、蓝通道组合成单个阵列,并按PWLCM序列排序。排列矢量被分解成代表三个通道的三个部分,并使用Lorenz混沌序列重新独立排序。然后将彩色图像的每个像素独立编码到DNA碱基中,DNA规则的选择是混乱的。通过与DNA规则的异或运算,提出了一种新的像素级混淆机制,增强了DNA互补规则的使用。这个过程是循环的,它有异或操作的起点,然后继续随机次数。著名的Chen超混沌序列被用来选择一个起始DNA规则和上限来继续异或操作替换一个像素。最后将替换的DNA碱基转化为数字格式,得到加密图像。
相关工作
在该算法中,采用了三个不同维数的混沌系统来增加复杂性,每个混沌系统都有自己的特点。
PWLCM
分段线性混沌映射(Piecewise Linear Chaotic Map)公式如下:
a
i
+
1
=
{
a
i
/
p
0
0
≤
a
i
<
p
0
(
a
i
−
p
0
)
/
(
0.5
−
p
0
)
p
0
≤
a
i
<
0.5
(
1
−
a
i
)
a
i
≥
0.5
a_{i+1}= \left\{ \begin{array}{lr} a_i/p_0 \ 0 \leq a_i <p_0 \\ (a_i-p_0)/(0.5-p_0) \ p_0 \leq a_i <0.5\\ (1-a_i)\ a_i \geq 0.5 \end{array} \right .
ai+1=⎩⎨⎧ai/p0 0≤ai<p0(ai−p0)/(0.5−p0) p0≤ai<0.5(1−ai) ai≥0.5
Chen’s hyper-chaotic system
Chen超混沌系统对初值和控制参数高度敏感,公式如下:
{
u
˙
=
a
(
v
−
u
)
v
˙
=
−
u
w
+
d
u
+
c
u
−
x
w
˙
=
u
v
−
b
w
x
˙
=
u
+
k
\left\{ \begin{array}{lr} \dot{u} =a(v-u) \\ \dot{v}=-uw+du+cu-x \\ \dot{w}=uv-bw \\ \dot{x}=u+k \end{array} \right .
⎩⎪⎪⎨⎪⎪⎧u˙=a(v−u)v˙=−uw+du+cu−xw˙=uv−bwx˙=u+k
a, b, c, d, k为系统参数,当a = 36, b = 3, c = 28, d = 16,−0.7≤k≤0.7时,陈氏超混沌系统处于混沌状态,可以产生4个混沌序列。本文使用参数k = 0.2来生成Chen混沌序列,本文采用四阶龙格-库塔法求解方程组,得到序列U、V、W和X,然后序列组合成一个数组。
Lorenz’s system
Lorenz系统是天气预报的数学模型,公式如下:
{
y
˙
=
−
f
y
+
f
z
z
˙
=
r
y
−
z
−
y
q
q
˙
=
−
g
q
+
y
z
\left\{ \begin{array}{lr} \dot{y} =-fy+fz \\ \dot{z}=ry-z-yq \\ \dot{q}=-gq+yz \end{array} \right .
⎩⎨⎧y˙=−fy+fzz˙=ry−z−yqq˙=−gq+yz
上述方程是一个具有两个非线性的动态非线性系统:yq,yz。输入f、g、r为气流的常量物理特性,y为空气槽内对流电流的幅值,z为上升和下降电流的温差,q为空气槽内温度与常温的偏差。该非线性方程组不存在解析解,首先将其转化为迭代形式,然后计算数值解。数值解表明,当0 < r < 1时,系统整体具有稳定响应,当1 < r < 24时,系统也具有稳定的周期响应,当r为> 24,f = 10, g = 8/3时,系统产生混沌响应。
DNA complementary rules and algebraic operations
脱氧核糖核酸或简称DNA是一种存在于几乎所有生物体内的遗传物质。在人体中,DNA以A, G, C和T是成对的。这些碱基分别是腺嘌呤(A)、胞嘧啶©、鸟嘌呤(G)和胸腺嘧啶(T)。1953年,Watson和Crick在《自然》杂志上发表了一篇文章,定义了互补碱基配对的原理[28],也被称为互补规则。根据互补规则,每一对DNA碱基必须是互补的,就像A和T是互补的,C和G是互补的。二进制数字系统只由两个数字组成;0和1相互对立或互补。同理,00和11是互补的,01和10也是互补的。用上面讨论的A、C、G、T四个基来表示二进制序列00、11、10、01。DNA转化规则共有24种,但只有8种符合所示的Watson-Crick互补规则,如下表:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 00-A | 00-C | 00-G | 00-T | 00-C | 00-A | 00-T | 00-G |
| 01-C | 01-A | 01-T | 01-C | 01-T | 01-G | 01-G | 01-A |
| 10-G | 10-T | 10-A | 10-G | 10-A | 10-C | 10-C | 10-T |
| 11-T | 11-G | 11-C | 11-A | 11-G | 11-T | 11-A | 11-C |
一幅数字图像的像素强度在0到255之间,所以将8位像素强度值表示到DNA域只需要4个DNA碱基。例如,如果像素强度值为93,则其二进制值为“01 01 11 01”,93的DNA转化值取决于DNA编码规则的选择,如果采用DNA编码规则8,它将成为“AACA”。利用相同的DNA规则8将“AACA”转换为数字格式,得到相同的强度值93。但如果我们选择另一条DNA规则解码,如规则1,那么“AACA”将是‘00 00 01 00’,像素的强度值将是2。这是DNA编码/解码方法。
DNA碱基存在加法(+)、减法(-)等代数运算和异或(XOR)。下表只展示了XOR运算,将在本文的方案中应用。
| XOR | A | G | C | T |
|---|---|---|---|---|
| A | A | G | C | T |
| G | G | A | T | C |
| C | C | T | A | G |
| T | T | C | G | A |
本文方案
生成初始条件
SHA-256生成256位的摘要,而不管输入的大小。如果两个输入之间有一个比特的差异,它们的消息摘要将完全不同。因此,这可以用来生成要加密的彩色图像的摘要,然后消息摘要分为两组十六进制值。第一组分为大小相同的8块,其值分别为
m
j
,
j
=
1
,
2...
,
8
m_j,j=1,2...,8
mj,j=1,2...,8。;每个块包含7个十六进制数字,通过公式将其转换为浮点小数
m
j
∈
(
0
,
0.0156
)
m_j∈(0, 0.0156)
mj∈(0,0.0156)
m
j
=
h
e
x
2
d
e
c
(
m
1
,
.
.
.
,
m
8
)
/
2
34
m_j = hex2dec(m_1,..., m_8)/2^{34}
mj=hex2dec(m1,...,m8)/234
第二部分直接转成浮点数
d
∈
(
0
,
0.0156
)
d∈(0, 0.0156)
d∈(0,0.0156)。
d
=
h
e
x
2
d
e
c
(
d
)
/
2
38
d = hex2dec(d)/2^{38}
d=hex2dec(d)/238
PWLCM初值为
{
a
0
′
=
a
0
+
m
1
+
C
K
p
0
′
=
p
0
+
m
2
+
C
K
m
o
d
1
\left\{ \begin{array}{lr} a'_0=a_0+m_1+CK \\ p'_0=p_0 + m_2 +CK \\ \end{array} \right . mod\ 1
{a0′=a0+m1+CKp0′=p0+m2+CKmod 1
Chen 系统新的初值为:
{
u
0
′
=
u
0
+
m
3
+
C
K
v
0
′
=
v
0
+
m
4
+
C
K
w
0
′
=
w
0
+
m
5
+
C
K
x
0
′
=
x
0
+
m
6
+
C
K
m
o
d
1
\left\{ \begin{array}{lr} u'_0=u_0 + m_3 + CK \\ v'_0=v_0 + m_4 +CK \\ w'_0=w_0 + m_5 + CK \\ x'_0=x_0 + m_6 +CK \\ \end{array} \right . mod\ 1
⎩⎪⎪⎨⎪⎪⎧u0′=u0+m3+CKv0′=v0+m4+CKw0′=w0+m5+CKx0′=x0+m6+CKmod 1
Lorenz 超混沌系统初值为:
{
y
0
′
=
y
0
+
m
7
+
C
K
z
0
′
=
z
0
+
m
8
+
C
K
q
0
′
=
q
0
+
d
+
C
K
m
o
d
1
\left\{ \begin{array}{lr} y'_0=y_0 + m_7 + CK \\ z'_0=z_0 + m_8 +CK \\ q'_0=q_0 + d + CK \end{array} \right . mod\ 1
⎩⎨⎧y0′=y0+m7+CKz0′=z0+m8+CKq0′=q0+d+CKmod 1
在上述方程中,CK是生成的通用密钥,如下所示
C
K
=
a
0
+
p
0
+
u
0
+
v
0
+
w
0
+
x
0
+
y
0
+
z
0
+
q
0
m
o
d
1
CK=a_0+p_0+u_0+v_0+w_0+x_0+y_0+z_0+q_0\ mod\ 1
CK=a0+p0+u0+v0+w0+x0+y0+z0+q0 mod 1
密钥对明文图像的依赖性确保了每次输入都会改变,因此使得加密图像更加安全。
置乱
本文提出的彩色图像的置乱方法分两次进行,第一次是采用PWLCM迭代3MN次得到的混沌序列A,将图像I的所有三个通道合并成一个1*3MN大小的一维数组,然后根据混沌序列A进行排序。
A = a i , a i + 1 , . . . , a 3 M N A={a_i,a_{i+1},...,a_{3MN}} A=ai,ai+1,...,a3MN
[ v a l A , i d x A ] = s o r t ( A ) [valA,idxA]=sort(A) [valA,idxA]=sort(A)
I ′ = I ( i d x A ) I'=I(idxA) I′=I(idxA)
之后,I’被分成3个1*MN大小的R、G、B通道
R = [ I ′ ( 1 ) , I ′ ( 2 ) , . . . I ′ ( M N ) ] R=[I'(1),I'(2),...I'(MN)] R=[I′(1),I′(2),...I′(MN)]
G = [ I ′ ( M N + 1 ) , I ′ ( M N + 2 ) , . . . , I ′ ( 2 M N ) ] G=[I'(MN+1),I'(MN+2),...,I'(2MN)] G=[I′(MN+1),I′(MN+2),...,I′(2MN)]
B = [ I ′ ( 2 M N + 1 ) , I ′ ( 2 M N + 2 ) , . . . , I ′ ( 3 M N ) ] B=[I'(2MN+1),I'(2MN+2),...,I'(3MN)] B=[I′(2MN+1),I′(2MN+2),...,I′(3MN)]
第二次排列分别在上述通道R、G和B上进行。用初值为 y 0 ′ , z 0 ′ , q 0 ′ y'_0,z'_0,q'_0 y0′,z0′,q0′的Lorenz系统生成大小为t+MN的三个伪随机序列Y、Z、Q去混淆三个通道的像素。为了避免瞬态效应,丢弃序列的前t个值,三个序列排序如下:
[ v a l Y , i d x Y ] = s o r t ( Y ) [valY,idxY]=sort(Y) [valY,idxY]=sort(Y)
[ v a l Z , i d x Z ] = s o r t ( Z ) [valZ,idxZ]=sort(Z) [valZ,idxZ]=sort(Z)
[ v a l Q , i d x Q ] = s o r t ( Q ) [valQ,idxQ]=sort(Q) [valQ,idxQ]=sort(Q)
其中idxY、idxZ、idxQ为已排序的Y、Z、Q的索引值,根据idxY、idxZ、idxQ对R、G、B中的元素进行重新排列,得到排列后的图像,如下式所示:
{
R
′
(
i
)
=
R
(
i
d
x
Y
(
i
)
)
G
′
(
i
)
=
G
(
i
d
x
Z
(
i
)
)
B
′
(
i
)
=
B
(
i
d
x
Q
(
i
)
)
\left\{ \begin{array}{lr} R'(i) = R(idxY(i)) \\ G'(i) = G(idxZ(i)) \\ B'(i) = B(idxQ(i)) \\ \end{array} \right .
⎩⎨⎧R′(i)=R(idxY(i))G′(i)=G(idxZ(i))B′(i)=B(idxQ(i))
DNA编码
将图像编码到DNA碱基很简单,对R、G、B通道的编码采用四种DNA规则,如下表。
| S# | Chaotic intervals | Encoding | Decoding |
|---|---|---|---|
| 1 | 0.001-0.05, 0.20-0.25, 0.40-0.45, 0.50-0.55, 0.95-0.99 | “AGCT” | “GTAC” |
| 2 | 0.05-0.10, 0.30-0.35, 0.60-0.65, 0.70-0.75, 0.85-0.90 | “ACGT” | “TGCA” |
| 3 | 0.10-0.15, 0.35-0.40, 0.55-0.60, 0.65-0.70, 0.80-0.85 | “GATC” | “CTAG” |
| 4 | 0.15-0.20, 0.25-0.30, 0.45-0.50, 0.75-0.80, 0.90-0.95 | “CATG” | “TCGA” |
把每个通道的像素转成二进制,用初始密钥
u
0
′
,
v
0
′
,
w
0
′
u'_0,v'_0,w'_0
u0′,v0′,w0′和
x
0
′
x'_0
x0′的Chen超混沌系统迭代(t+MN*3)次得到四个伪随机混沌序列U,V,W和X。为了消除瞬态效应,消除前t个元素。U的元素被分成三个大小为MN的向量;
{
U
1
=
[
U
(
1
)
,
U
(
2
)
,
.
.
.
,
U
(
M
N
)
]
U
2
=
[
U
(
M
N
+
1
)
,
U
(
M
N
+
2
)
,
.
.
.
,
U
(
2
M
N
)
]
U
3
=
[
U
(
2
M
N
+
1
)
,
U
(
2
M
N
+
2
)
,
.
.
.
,
U
(
3
M
N
)
]
\left \{ \begin{array}{lr} U_1=[U(1),U(2),...,U(MN)] \\ U_2=[U(MN+1),U(MN+2),...,U(2MN)] \\ U_3=[U(2MN+1),U(2MN+2),...,U(3MN)] \end{array}\ \right .
⎩⎨⎧U1=[U(1),U(2),...,U(MN)]U2=[U(MN+1),U(MN+2),...,U(2MN)]U3=[U(2MN+1),U(2MN+2),...,U(3MN)]
现在,应用新的DNA编码模型去独立地编码每个通道,每个DNA碱基数组大小为14MN
KaTeX parse error: Undefined control sequence: \ at position 137: …) \end{array}\̲ ̲ \right .
混淆/扩散
对彩色图像的三个通道进行编码,以一种新颖的方式对每个像素进行异或运算,并使用DNA规则本身。该方法需要两个确定性随机数数组,一个混沌序列用于选择DNA规则,另一个混沌序列用于决定重复时间,以继续与后续的DNA规则进行异或操作。利用上述Chen系统生成的随机序列V和W,将其转换为start{0,1,2,3,4,5,6,7}和times{0,1,2,3,4,5,6,7},
{
s
t
a
r
t
=
(
V
(
i
)
×
1
0
12
)
m
o
d
8
t
i
m
e
s
=
(
W
(
i
)
×
1
0
12
)
m
o
d
8
i
=
1
,
2
,
.
.
.
,
3
M
N
\left \{ \begin{array}{lr} start =(V(i) × 10^{12})mod\ 8\\ times=(W(i)×10^{12})mod\ 8 \end{array}\ i=1,2,...,3MN \right .
{start=(V(i)×1012)mod 8times=(W(i)×1012)mod 8 i=1,2,...,3MN
把start和times分割成三个大小为MN的子数组,如下式:
{
s
t
a
r
t
R
=
[
s
t
a
r
t
(
1
)
,
s
t
a
r
t
(
2
)
,
.
.
.
,
s
t
a
r
t
(
M
N
)
]
s
t
a
r
t
G
=
[
s
t
a
r
t
(
M
N
+
1
)
,
s
t
a
r
t
(
M
N
+
2
)
,
.
.
.
,
s
t
a
r
t
(
2
M
N
)
]
s
t
a
r
t
B
=
[
s
t
a
r
t
(
2
M
N
+
1
)
,
s
t
a
r
t
(
2
M
N
+
2
)
,
.
.
.
,
s
t
a
r
t
(
3
M
N
)
]
\left\{ \begin{array}{lr} start_R=[start(1),start(2),...,start(MN)] \\ start_G=[start(MN+1),start(MN+2),...,start(2MN)] \\ start_B=[start(2MN+1),start(2MN+2),...,start(3MN)] \end{array} \right .
⎩⎨⎧startR=[start(1),start(2),...,start(MN)]startG=[start(MN+1),start(MN+2),...,start(2MN)]startB=[start(2MN+1),start(2MN+2),...,start(3MN)]
{
t
i
m
e
s
R
=
[
t
i
m
e
s
(
1
)
,
t
i
m
e
s
(
2
)
,
.
.
.
,
t
i
m
e
s
(
M
N
)
]
t
i
m
e
s
G
=
[
t
i
m
e
s
(
M
N
+
1
)
,
t
i
m
e
s
(
M
N
+
2
)
,
.
.
.
,
t
i
m
e
s
(
2
M
N
)
]
t
i
m
e
s
B
=
[
t
i
m
e
s
(
2
M
N
+
1
)
,
t
i
m
e
s
(
2
M
N
+
2
)
,
.
.
.
,
t
i
m
e
s
(
3
M
N
)
]
\left\{ \begin{array}{lr} times_R=[times(1),times(2),...,times(MN)] \\ times_G=[times(MN+1),times(MN+2),...,times(2MN)] \\ times_B=[times(2MN+1),times(2MN+2),...,times(3MN)] \end{array} \right .
⎩⎨⎧timesR=[times(1),times(2),...,times(MN)]timesG=[times(MN+1),times(MN+2),...,times(2MN)]timesB=[times(2MN+1),times(2MN+2),...,times(3MN)]
使用start_R和times_R替换排列和编码红色通道的像素伪代码如下:
for i =1 to MN
pixel = R_DNA(i,∀)
s=start_R(i)
for k=1 to times_R(i)
pixel=pixel ⊗ Rule(s)
s=(s+1) mod 8
end
RED(i)=pixel
end
上述伪代码将执行MN次,用适当的变量替换R_DNA,start_R,times_R,得到三个替换通道。在上面的伪代码中,∀表示一个像素的四个DNA碱基。
解码
基于大小为3MN的伪随机数组X,从DNA编码表中随机选取4条DNA rules,实现对红、绿、蓝通道的解码。在编码过程中生成的数组仍然可以自由使用,将向量X分成三个数组,如下所示:
{
X
1
=
E
[
X
(
1
)
,
X
(
2
)
,
.
.
.
,
X
(
M
N
)
]
X
2
=
[
X
(
M
N
+
1
)
,
X
(
M
N
+
2
)
,
.
.
.
,
X
(
2
M
N
)
]
X
3
=
[
X
(
2
M
N
+
1
)
,
X
(
2
M
N
+
2
)
,
.
.
.
,
X
(
3
M
N
)
]
\left\{ \begin{array}{lr} X_1=E[X(1),X(2),...,X(MN)] \\ X_2=[X(MN+1),X(MN+2),...,X(2MN)] \\ X_3=[X(2MN+1),X(2MN+2),...,X(3MN)] \end{array} \right .
⎩⎨⎧X1=E[X(1),X(2),...,X(MN)]X2=[X(MN+1),X(MN+2),...,X(2MN)]X3=[X(2MN+1),X(2MN+2),...,X(3MN)]
{ C i p h e r _ R E D = D e c o d e ( R E D ( i ) , X 1 ) C i p h e r _ G R E E N = D e c o d e ( G R E E N ( i ) , X 2 ) C i p h e r _ B L U E = D e c o d e ( B L U E ( i ) , X 3 ) \left\{ \begin{array}{lr} Cipher\_RED=Decode(RED(i),X_1) \\ Cipher\_GREEN=Decode(GREEN(i),X_2) \\ Cipher\_BLUE=Decode(BLUE(i),X_3) \end{array} \right . ⎩⎨⎧Cipher_RED=Decode(RED(i),X1)Cipher_GREEN=Decode(GREEN(i),X2)Cipher_BLUE=Decode(BLUE(i),X3)
扩散过程说明
假设红通道的一个像素由DNA碱基{A, C, T, T}组成,start_R={4},times_R={6},则{A, C, T,
T}将与规则GTAC异或,然后是ACGT, TCGA, CATG, AGCT和GATC
| s# | Selection Value | DNA Rules for XOR |
|---|---|---|
| 1 2 3 4 5 6 7 8 | 0 1 2 3 4 5 6 7 | AGCT GATC CTAG TGCA GTAC ACGT TC GA CATG |
结果将在每次迭代时生成
- {G, G, T, G} = {A, C, T, T}⊗{G, T, A, C} or Rule 4
- {G, T, C, C} = {G, G, T, G}⊗{A, C, G, T} or Rule 5
- {C, G, T, C} = {G, T, C, C}⊗{T, C, G, A} or Rule 6
- {A, G, A, T} = {C, G, T, C}⊗{C, A, T, G} or Rule 7
- {A, A, C, A} = {A, G, A, T}⊗{A, G, C, T} or Rule 0
- {G, A, G, C} = {A, A, C, A}⊗{G, A, T, C} or Rule 1
最终的输出是{G, A, G, C}。DNA规则{4,5,6,7,0,1}在序列中是互斥的。
图像加密步骤
假设原始彩色图像I的大小为M × N × 3,完整的加密过程包括以下步骤。
**输入:**图像I,PWLCM, Chen’s和Lorenz’s系统通用的初始条件和控制参数 a 0 , p 0 , u 0 , v 0 , w 0 , x 0 , y 0 , z 0 , q 0 , a_0, p_0, u_0, v_0, w_0, x_0, y_0, z_0, q_0, a0,p0,u0,v0,w0,x0,y0,z0,q0, 。
**输出:**加密后的图像。
**步骤1:**计算明文图像的SHA-256哈希值,生成新的初始条件;
**步骤2:**转换彩色图像I为3MN的1维数组然后用新的 a 0 ′ , p 0 ′ a'_0,p'_0 a0′,p0′初值得到混沌序列A。之后重新排列一维数组然后分成三个大小为1*MN的R、G、B分量;
**步骤3:**迭代初值为 y 0 ′ , z 0 ′ y'_0,z'_0 y0′,z0′和 q 0 ′ q'_0 q0′的混沌系统得到三个大小为1*MN的序列,重新排序R,G,B三个独立通道;
**步骤4:**迭代初值为 u 0 ′ , v 0 ′ , w 0 ′ u'_0,v'_0,w'_0 u0′,v0′,w0′和 x 0 ′ x'_0 x0′的Chen混沌系统得到四个大小为1*3MN的伪随机序列U,V,W和X。把U分割成三个子向量 U 1 , U 2 U_1,U_2 U1,U2和 U 3 U_3 U3,这些子向量被用来选择DNA编码规则去转换每个颜色通道的像素为DNA碱基;
**步骤5:**对每个像素的混淆,序列V和W被转成0-7的十进制值,被称为start和times并且每个都可以分成三个子数组start_R,start_G,start_B,times_R,times_G,times_B;
**步骤6:**在每个通道上使用上述伪代码实现通道替换;
**步骤7:**将X分成三个子向量X1、X2、X3,根据DNA编码表选择解码规则将每个颜色通道的每个像素转成数字格式;
**步骤8:**结合三个解码通道得到加密彩色图像;
解密过程
在上面的例子中,start_R={4},times_R={6},在加密过程中,应用DNA规则{4,5,6,7,0,1},但解密时,必须反向应用DNA规则才能得到明文的像素。所以(4 + 6)−1 = 9 mod 8 = 1所以,DNA规则
应用{1,0,7,6,5,4}。解密的伪代码如下:
for i =1 to MN
pixel = R_DNA(i,∀)
s={[start_R(i)+times_R(i)]-1}mod 8
for k=1 to times_R(i)
pixel=pixel ⊗ Rule(s)
s=(s-1) mod 8
end
RED(i)=pixel
end
实验结果
初始条件
PWLCM映射初始值为: a 0 = 0.123456789010 , p 0 = 0.234578900 a_0=0.123456789010,p_0=0.234578900 a0=0.123456789010,p0=0.234578900。
Chen超混沌系统初始值: u 0 = 0.3456789012 , v 0 = 0.245789012 , w 0 = 0.4567890124 , x 0 = 0.5678901234 u_0=0.3456789012,v_0= 0.245789012,w_0=0.4567890124,x_0=0.5678901234 u0=0.3456789012,v0=0.245789012,w0=0.4567890124,x0=0.5678901234。
Lorenz系统初始值: y 0 = 0.6789012346 , z 0 = 0.7890123456 , q 0 = 0.6890123450 y_0=0.6789012346,z_0=0.7890123456,q_0=0.6890123450 y0=0.6789012346,z0=0.7890123456,q0=0.6890123450
密钥集: γ 0 = [ a 0 ′ , p 0 ′ , u 0 ′ , v 0 ′ , w 0 ′ , x 0 ′ , y 0 ′ , z 0 ′ , q 0 ′ ] . \gamma_0 = [a'_0, p'_0, u'_0, v'_0, w'_0, x'_0, y'_0, z'_0, q'_0]. γ0=[a0′,p0′,u0′,v0′,w0′,x0′,y0′,z0′,q0′].
Chen系统控制参数: a = 36 , b = 3 , c = 28 , d = 16 , k = 0.2 a=36,b=3,c=28,d=16,k=0.2 a=36,b=3,c=28,d=16,k=0.2
Lorenz系统控制参数: f = 10 , g = 8 / 3 , r = 28 f=10,g=8/3,r=28 f=10,g=8/3,r=28
用Lean作为明文图片对所提出的加密方案进行评价和测试
加解密结果如下:
性能评估
注:性能评估代码参见【常见图像加密性能评价指标】
密钥空间分析
混沌系统输入浮点精度取决于系统在 1 0 10 到 1 0 12 10^{10}到10^{12} 1010到1012之间的变化,本文采用了PWLCM、Lorenz、Chen三种混沌系统。PWLCM采用了精度为 1 0 12 10^{12} 1012的两个参数 a0和p0,因此PWLCM的密钥空间为 $S_{PWLCM}=S_{a0}*S_{p0}\approxeq 10^{24}\approxeq 2^{79.72} $。第二个混沌系统是Chen系统,需要四个输入。Chen系统的初始值精度为 1 0 1 0 10^10 1010,因此Chen系统的密钥空间是 S C h e n ′ s = S u 0 ∗ S v 0 ∗ S w 0 ∗ S x 0 ≊ 1 0 40 ≊ 2 132.87 S_{Chen's}=S_{u0}*S_{v0}*S_{w0}*S_{x0}\approxeq 10_{40}\approxeq 2^{132.87} SChen′s=Su0∗Sv0∗Sw0∗Sx0≊1040≊2132.87。第三个系统是Lorenz系统,需要三个初始值。 S l o r e n z = S y 0 ∗ S z 0 ∗ S 10 = 1 0 30 ≊ 2 99.65 S_{lorenz}=S_{y0}*S_{z0}*S_{10}=10^{30}\approxeq 2^{99.65} Slorenz=Sy0∗Sz0∗S10=1030≊299.65。总密钥空间是 S T o t a l = S P W L C M ∗ S C h e n ∗ S L o r e n z = 1 0 94 ≊ 2 312 S_{Total}=S_{PWLCM}*S_{Chen}*S_{Lorenz}=10^{94}\approxeq 2^{312} STotal=SPWLCM∗SChen∗SLorenz=1094≊2312。所提出系统的密钥空间远大于抵抗暴力攻击的最小要求 2 128 2^{128} 2128。
密钥敏感度测试
密钥敏感度测试可以通过修改密钥 K 中的某一位得到 K’,利用 K 和 K’ 加密同一张图像得到𝐶1和𝐶2,采用像素改变率 NPCR 和像素平均改变强度 UACI 量化两张密文图像的差别。NPCR 和 UACI 越接近理想值,加密算法对安全密钥 的敏感度越强,加密算法越安全。
| NPCR | UACI | |
|---|---|---|
| R | 99.5686% | 33.4380% |
| G | 99.6098% | 33.4592% |
| B | 99.6178% | 33.4337% |
直方图分析
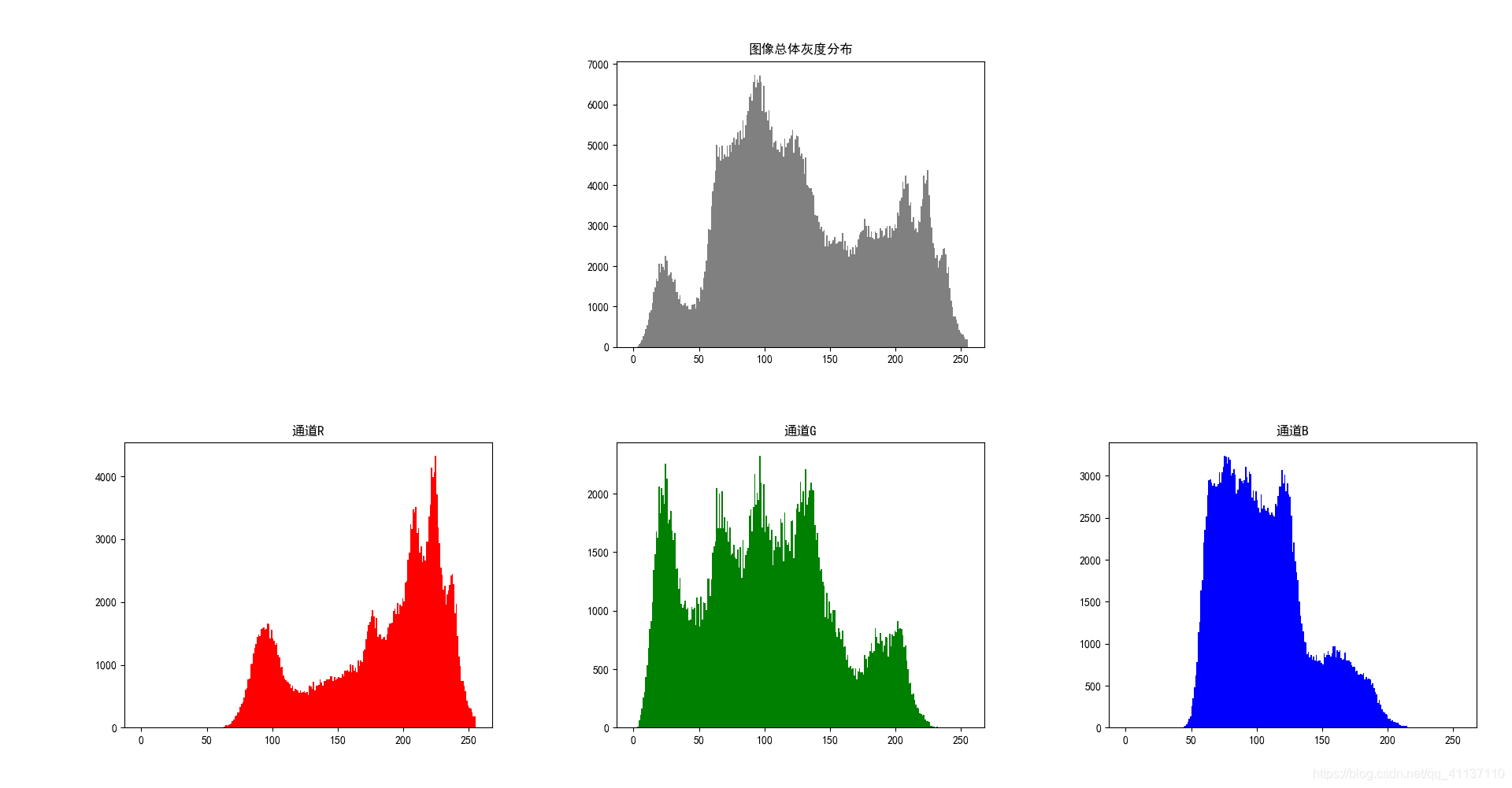
原始图像Lena.png的灰度直方图如下
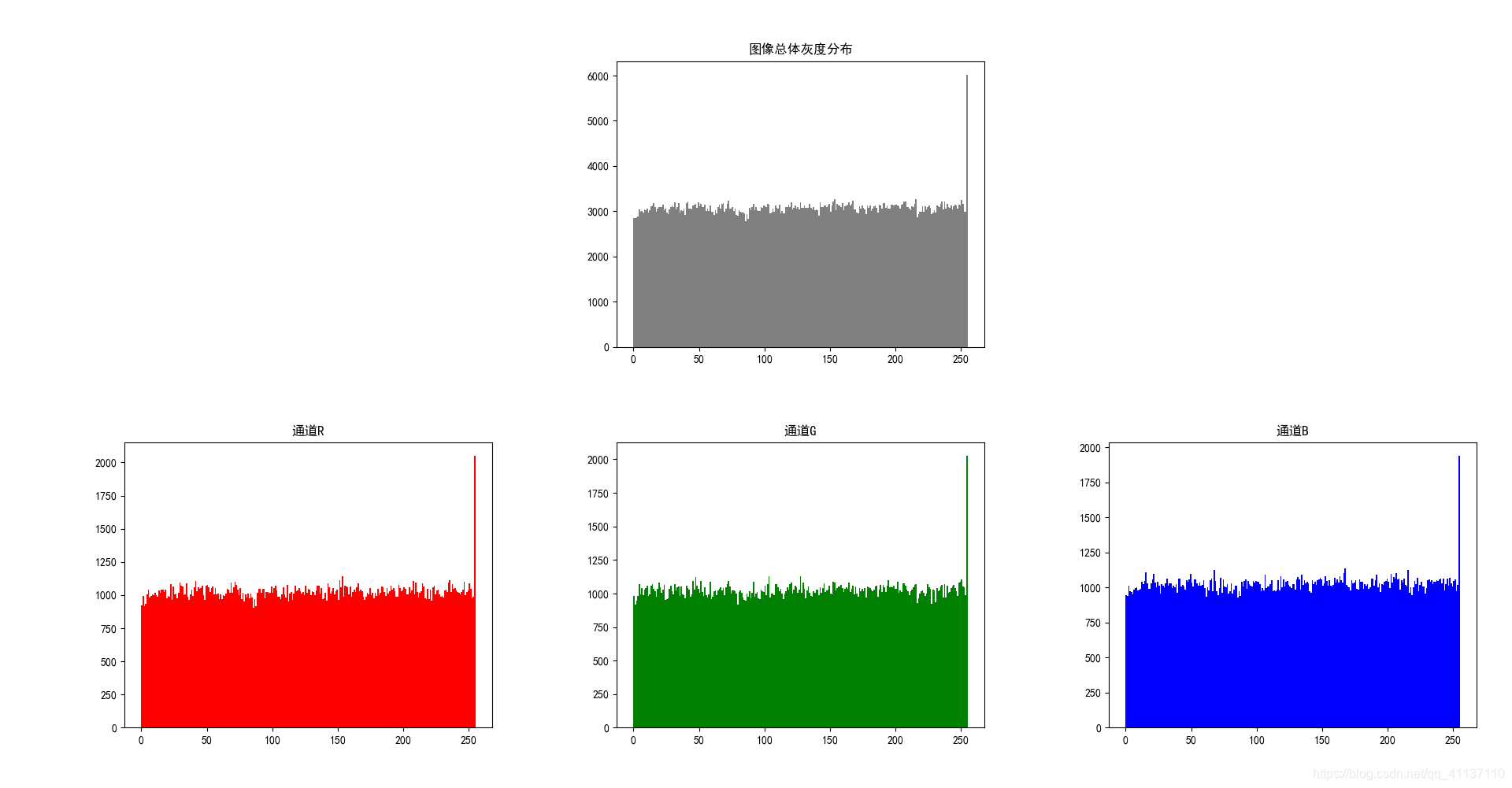
加密图像Lena_encrypt1.png的灰度直方图如下:
相关性分析
原始图像的相关系数
| 通道 | Horizontal | Vertical | Diagonal |
|---|---|---|---|
| R | 0.9782 | 0.9893 | 0.9664 |
| G | 0.9699 | 0.9805 | 0.9548 |
| B | 0.9359 | 0.9572 | 0.9239 |
加密图像的相关系数
| 通道 | Horizontal | Vertical | Diagonal |
|---|---|---|---|
| R | -0.0110 | -0.0091 | 0.0223 |
| G | -0.0260 | -0.0175 | -0.0228 |
| B | -0.0147 | -0.0078 | -0.0114 |
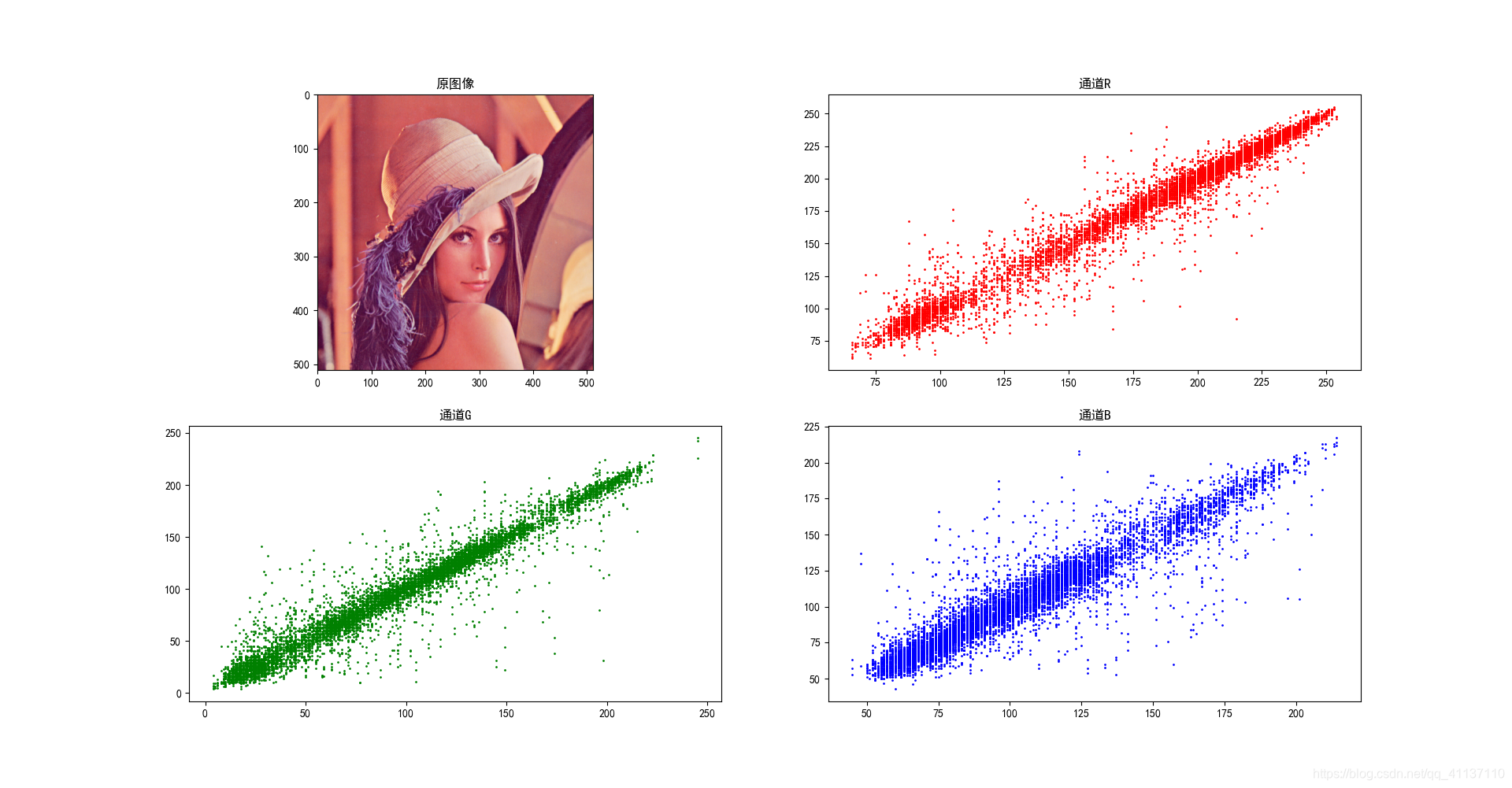
原始图像相关性图
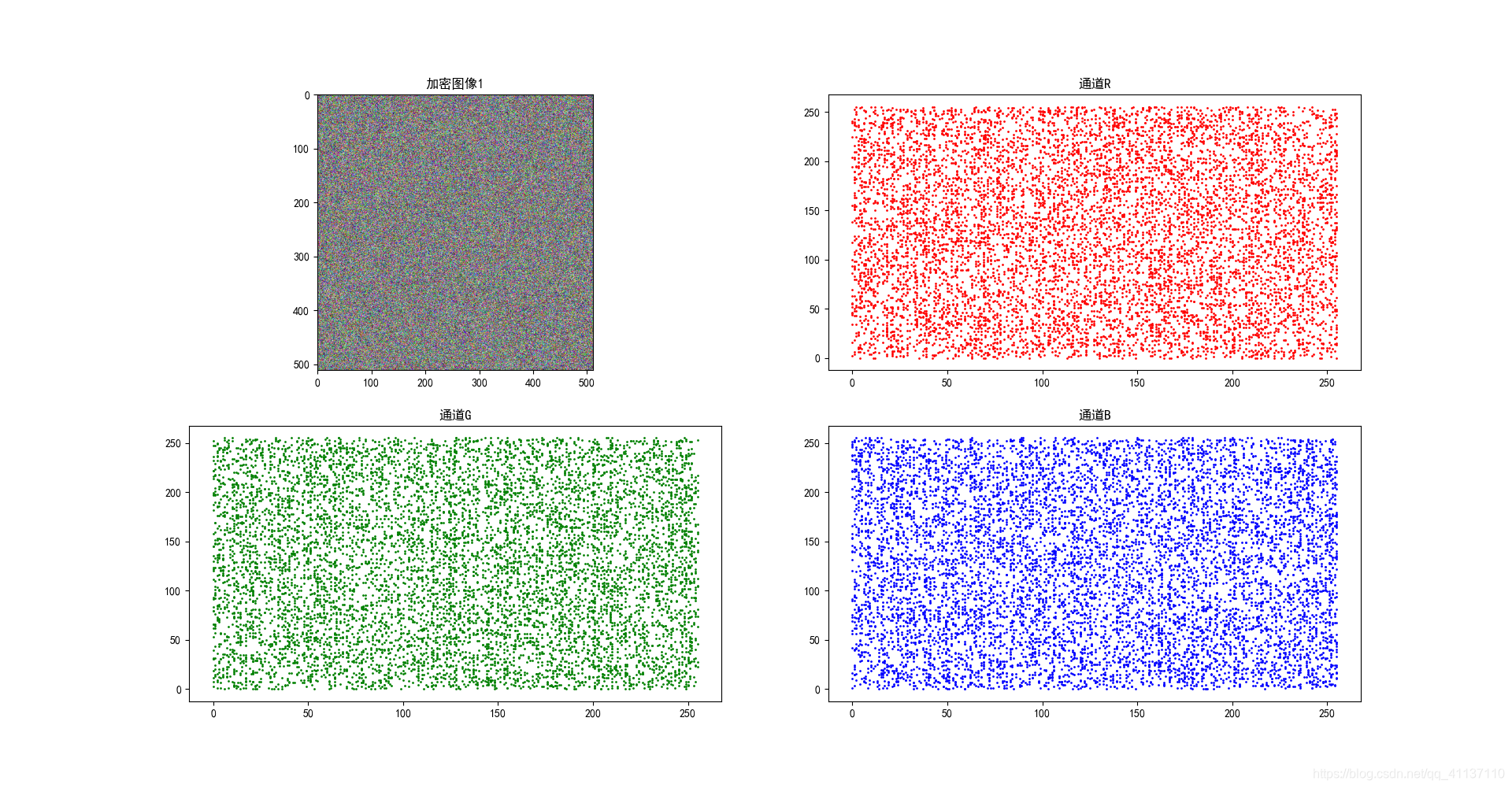
加密图像相关性图
信息熵
| 信息熵计算 | 原Lena图像 | 加密图像1 |
|---|---|---|
| R | 6.879 | 7.999 |
| G | 6.926 | 7.999 |
| B | 6.968 | 7.999 |
噪声攻击
对加密图像分别添加均值为零,方差为0.0005的高斯噪声和5%的校验噪声,然后进行解密,结果如下
裁剪攻击
从加密图像中移除(换成0)一块80×80像素的红色通道,一块50×80像素的绿色通道和一块60×50像素的全通道,然后进行解密,结果如图。
峰值信噪比(PSNR)
与原始图像计算PSNR
| PSNR | 加密图像 | Gauss噪声解密图像 | 椒盐噪声解密图像 | 裁剪解密图像 |
|---|---|---|---|---|
| R | 7.895123 | 17.676579 | 20.855574 | 24.268677 |
| G | 8.562234 | 18.183927 | 21.599919 | 24.585058 |
| B | 9.603804 | 19.269221 | 22.659644 | 25.684638 |
差分攻击
使用两个测试图像,一个是明文图像Lena,另一个是改变了一位像素的图像,把右下角的像素R通道值从185(0b10111001)改成了184(0b10111000)。c1和c2是两张明文图像相应的加密图像,两幅密文图像的NPCR和UACI计算结果如下
| NPCR | UACI | |
|---|---|---|
| R | 99.5964% | 33.4411% |
| G | 99.6056% | 33.4552% |
| B | 99.6181% | 33.4561% |
实验代码
import cv2
import hashlib
import numpy as np
import matplotlib.pyplot as plt
'''
加密函数
img:原始图像路径
key:密钥列表,大小为9(1、2为PWLCM初始条件和参数;3、4、5、6为Chen系统初值,7、8、9为Lorenz系统初值)
return:返回加密后的图像
'''
def encrypt(img,key):
#读取图片
#opencv的颜色通道顺序为[B,G,R],而matplotlib颜色通道顺序为[R,G,B],所以需要调换一下通道位置
im=cv2.imread(img)[:,:,(2,1,0)]
#获取图像宽高和通道数
[w,h,dim]=im.shape
#生成初始条件
a0=key[0]
p0=key[1]
u0=key[2]
v0=key[3]
w0=key[4]
x0=key[5]
y0=key[6]
z0=key[7]
q0=key[8]
#两次置乱操作
#图像扁平化为一维,flatten in row-major
pixels = im.flatten(order = 'C')
#第一次置乱
#PWLCM迭代3*w*h次,得到迭代序列ai
ai=[]
for i in range(3*w*h):
if 0<=a0<p0:
a0=a0/p0
elif a0<0.5:
a0=(a0-p0)*(0.5-p0)
else:
a0=1-a0
ai.append(a0)
#打包
dic=list(zip(ai,pixels))
#根据ai排序
dic.sort(key=lambda x:x[0])
#得到排序后的像素列表
pixels=list(list(zip(*dic))[1])
#分成R、G、B三个通道
R=pixels[:w*h]
G=pixels[w*h:2*w*h]
B=pixels[2*w*h:]
#第二次置乱
#Lorenz生成三个序列Y,Z,Q
t=100
f=10
r=28
g=8/3
#调用Lorenz模型函数
Y,Z,Q=Lorenz(y0,z0,q0,f,r,g,t+w*h)
#丢弃序列前t个值
Y=Y[t:]
Z=Z[t:]
Q=Q[t:]
#分别在R、G、B三个通道进行排序
Y_R=list(zip(Y,R))
#根据序列Y排序
Y_R.sort(key=lambda x:x[0])
#得到排序后的像素列表
R=list(list(zip(*Y_R))[1])
Z_G=list(zip(Z,G))
#根据序列Z排序
Z_G.sort(key=lambda x:x[0])
#得到排序后的像素列表
G=list(list(zip(*Z_G))[1])
Q_B=list(zip(Q,B))
#根据序列Q排序
Q_B.sort(key=lambda x:x[0])
#得到排序后的像素列表
B=list(list(zip(*Q_B))[1])
#得到重新排列后的R、G、B颜色分量
#DNA编码
#Hyper Chaos Chen系统控制参数
a=36
b=3
c=28
d=16
k=0.2
t=100
U,V,W,X=Chen(u0,v0,w0,x0,a,b,c,d,k,t+3*w*h)
U=U[t:]
V=V[t:]
W=W[t:]
X=X[t:]
for i in range(3*w*h):
rule='ACGT'
if(int(U[i]%1/0.05) in [0,4,8,10,19]):
#采用编码规则AGCT
rule='AGCT'
elif(int(U[i]%1/0.05) in [1,6,12,14,17]):
#编码规则ACGT
rule='ACGT'
elif(int(U[i]%1/0.05) in [2,7,11,13,16]):
rule='GATC'
elif(int(U[i]%1/0.05) in [3,5,9,15,18]):
rule='CATG'
if(i/(w*h)<1):
R[i]=DNA_Encode(R[i],rule)
elif(i/(w*h)<2):
G[i-w*h]=DNA_Encode(G[i-w*h],rule)
else:
B[i-2*w*h]=DNA_Encode(B[i-2*w*h],rule)
start=[]
times=[]
for i in V:
start.append(int(i*pow(10,12))%8)
for i in W:
times.append(int(i*pow(10,12))%8)
startR=start[:w*h]
startG=start[w*h:2*w*h]
startB=start[2*w*h:]
timesR=times[:w*h]
timesG=times[w*h:2*w*h]
timesB=times[2*w*h:]
#八种DNA编码规则
rules=['ACGT','CATG','GTAC','TCGA','CTAG','AGCT','TGCA','GATC']
for i in range(w*h):
#起始规则位置
s=startR[i]
for j in range(timesR[i]):
R[i]=DNA_XOR(R[i],rules[s])
s=(s+1)%8
for i in range(w*h):
#起始规则位置
s=startG[i]
for j in range(timesG[i]):
G[i]=DNA_XOR(G[i],rules[s])
s=(s+1)%8
for i in range(w*h):
#起始规则位置
s=startB[i]
for j in range(timesB[i]):
B[i]=DNA_XOR(B[i],rules[s])
s=(s+1)%8
#DNA解码
for i in range(3*w*h):
rule='ACGT'
if(int(X[i]%1/0.05) in [0,4,8,10,19]):
#采用解码规则GTAC
rule='GTAC'
elif(int(X[i]%1/0.05) in [1,6,12,14,17]):
#解码规则TGCA
rule='TGCA'
elif(int(X[i]%1/0.05) in [2,7,11,13,16]):
rule='CTAG'
elif(int(X[i]%1/0.05) in [3,5,9,15,18]):
rule='TCGA'
if(i/(w*h)<1):
R[i]=DNA_Decode(R[i],rule)
elif(i/(w*h)<2):
G[i-w*h]=DNA_Decode(G[i-w*h],rule)
else:
B[i-2*w*h]=DNA_Decode(B[i-2*w*h],rule)
#合并R、G、B三个通道得到加密彩色图像
encrypt_img=np.array((R+G+B)).reshape((512,512,3),order='C')
return encrypt_img
'''
功能:加密图像解密,加密过程的逆
参数:
输入加密图像路径和密钥参数
返回:
返回解密后的图像(ndarray)
'''
def decrypt(img,key):
#生成初始条件
a0=key[0]
p0=key[1]
u0=key[2]
v0=key[3]
w0=key[4]
x0=key[5]
y0=key[6]
z0=key[7]
q0=key[8]
#读取密文图像
# im=cv2.imread(img)[:,:,(2,1,0)]
im=cv2.imread(img)
#获取图像高宽和通道数
[h,w,dim]=im.shape
pixels = im.flatten(order = 'C')
#分成R、G、B三个通道
R=list(pixels[:w*h])
G=list(pixels[w*h:2*w*h])
B=list(pixels[2*w*h:])
#Hyper Chaos Chen系统控制参数
a=36
b=3
c=28
d=16
k=0.2
t=100
U,V,W,X=Chen(u0,v0,w0,x0,a,b,c,d,k,t+3*w*h)
U=U[t:]
V=V[t:]
W=W[t:]
X=X[t:]
for i in range(3*w*h):
rule='ACGT'
if(int(X[i]%1/0.05) in [0,4,8,10,19]):
#采用解码规则GTAC进行逆编码
rule='GTAC'
elif(int(X[i]%1/0.05) in [1,6,12,14,17]):
#解码规则TGCA
rule='TGCA'
elif(int(X[i]%1/0.05) in [2,7,11,13,16]):
rule='CTAG'
elif(int(X[i]%1/0.05) in [3,5,9,15,18]):
rule='TCGA'
if(i/(w*h)<1):
R[i]=DNA_Encode(R[i],rule)
elif(i/(w*h)<2):
G[i-w*h]=DNA_Encode(G[i-w*h],rule)
else:
B[i-2*w*h]=DNA_Encode(B[i-2*w*h],rule)
#逆扩散
start=[]
times=[]
for i in V:
start.append(int(i*pow(10,12))%8)
for i in W:
times.append(int(i*pow(10,12))%8)
startR=start[:w*h]
startG=start[w*h:2*w*h]
startB=start[2*w*h:]
timesR=times[:w*h]
timesG=times[w*h:2*w*h]
timesB=times[2*w*h:]
#八种DNA编码规则
rules=['ACGT','CATG','GTAC','TCGA','CTAG','AGCT','TGCA','GATC']
for i in range(w*h):
#起始规则位置
s=(startR[i]+timesR[i]-1)%8
for j in range(timesR[i]):
R[i]=DNA_XOR(R[i],rules[s])
s=(s-1)%8
for i in range(w*h):
#起始规则位置
s=(startG[i]+timesG[i]-1)%8
for j in range(timesG[i]):
G[i]=DNA_XOR(G[i],rules[s])
s=(s-1)%8
for i in range(w*h):
#起始规则位置
s=(startB[i]+timesB[i]-1)%8
for j in range(timesB[i]):
B[i]=DNA_XOR(B[i],rules[s])
s=(s-1)%8
#逆编码
for i in range(3*w*h):
rule='ACGT'
if(int(U[i]%1/0.05) in [0,4,8,10,19]):
#采用编码规则AGCT
rule='AGCT'
elif(int(U[i]%1/0.05) in [1,6,12,14,17]):
#编码规则ACGT
rule='ACGT'
elif(int(U[i]%1/0.05) in [2,7,11,13,16]):
rule='GATC'
elif(int(U[i]%1/0.05) in [3,5,9,15,18]):
rule='CATG'
if(i/(w*h)<1):
R[i]=DNA_Decode(R[i],rule)
elif(i/(w*h)<2):
G[i-w*h]=DNA_Decode(G[i-w*h],rule)
else:
B[i-2*w*h]=DNA_Decode(B[i-2*w*h],rule)
#逆第二次置乱
#Lorenz生成三个序列Y,Z,Q
t=100
f=10
r=28
g=8/3
#调用Lorenz模型函数
Y,Z,Q=Lorenz(y0,z0,q0,f,r,g,t+w*h)
#丢弃序列前t个值
Y=Y[t:]
Z=Z[t:]
Q=Q[t:]
#分别在R、G、B三个通道进行排序
seq=range(w*h)
Y_seq=list(zip(Y,seq))
#根据序列Y得到R通道真实的序列
Y_seq.sort(key=lambda x:x[0])
#得到真实序列,Y元素为位置索引
Y=list(list(zip(*Y_seq))[1])
Z_seq=list(zip(Z,seq))
Z_seq.sort(key=lambda x:x[0])
Z=list(list(zip(*Z_seq))[1])
Q_seq=list(zip(Q,seq))
Q_seq.sort(key=lambda x:x[0])
Q=list(list(zip(*Q_seq))[1])
Y_R=list(zip(Y,R))
Y_R.sort(key=lambda x:x[0])
R=list(list(zip(*Y_R))[1])
Z_G=list(zip(Z,G))
Z_G.sort(key=lambda x:x[0])
G=list(list(zip(*Z_G))[1])
Q_B=list(zip(Q,B))
Q_B.sort(key=lambda x:x[0])
B=list(list(zip(*Q_B))[1])
pixels=R+G+B
#逆第一次置乱
#PWLCM迭代3*w*h次,得到迭代序列ai
ai=[]
for i in range(3*w*h):
if 0<=a0<p0:
a0=a0/p0
elif a0<0.5:
a0=(a0-p0)*(0.5-p0)
else:
a0=1-a0
ai.append(a0)
seq=range(3*w*h)
ai_seq=list(zip(ai,seq))
#根据序列ai得到真实的序列
ai_seq.sort(key=lambda x:x[0])
#得到真实序列,ai元素为位置索引
ai=list(list(zip(*ai_seq))[1])
#打包
dic=list(zip(ai,pixels))
#根据ai排序
dic.sort(key=lambda x:x[0])
#得到排序后的像素列表
pixels=list(list(zip(*dic))[1])
decrypt_img=np.array(pixels).reshape((512,512,3),order='C')
return decrypt_img
'''
Lorenz吸引子生成函数
参数为三个初始坐标,三个初始参数,迭代次数
返回三个一维list
'''
def Lorenz(x0,y0,z0,p,q,r,T):
#微分迭代步长
h=0.01
x=[]
y=[]
z=[]
for t in range(T):
xt=x0+h*p*(y0-x0)
yt=y0+h*(q*x0-y0-x0*z0)
zt=z0+h*(x0*y0-r*z0)
#x0、y0、z0统一更新
x0,y0,z0=xt,yt,zt
x.append(x0)
y.append(y0)
z.append(z0)
return x,y,z
'''
Chen吸引子生成函数
参数为四个初始坐标,五个初始参数,迭代次数
返回四个一维数组(坐标)
'''
def Chen(u0,v0,w0,x0,a,b,c,d,k,T):
h=0.001
u=[]
v=[]
w=[]
x=[]
for t in range(T):
ut=u0+h*(a*(v0-u0))
vt=v0+h*(-u0*w0+d*u0+c*u0-x0)
wt=w0+h*(u0*v0-b*w0)
xt=u0+k
#u0、v0、w0,x0统一更新
u0,v0,w0,x0=ut,vt,wt,xt
u.append(u0)
v.append(v0)
w.append(w0)
x.append(x0)
return u,v,w,x
#根据原始图像使用SHA256生成初始条件
def Generate_Key(img,key):
im=cv2.imread(img)[:,:,(2,1,0)]
#获取图像高宽和通道数
[h,w,dim]=im.shape
with open(img,'rb') as f:
bytes=f.read()
img_hash=hashlib.sha256(bytes).hexdigest()
m=[]
for i in range(8):
m.append(int(img_hash[i*7:i*7+7],16)/2**34)
d=int(img_hash[-8:],16)/2**38
ck=0
for i in range(len(key)):
ck+=key[i]
#生成初始条件
for i in range(8):
key[i]=(key[i]+m[i]+ck)%1
key[8]=(key[8]+d+ck)%1
return key
#将像素值按照规则rule编码成DNA碱基返回
def DNA_Encode(pixel,rule):
base=''
#将整数像素值转成8bits二进制
bits=bin(pixel)[2:].zfill(8)
for k in range(4):
b=bits[k*2:2*k+2]
if b=='00':
base+=rule[0]
elif b=='01':
base+=rule[1]
elif b=='10':
base+=rule[2]
else:
base+=rule[3]
return base
#将4个DNA碱基组成的字符串按rule解码成像素值返回
def DNA_Decode(base,rule):
pixel=''
for k in base:
if k==rule[0]:
pixel+='00'
elif k==rule[1]:
pixel+='01'
elif k==rule[2]:
pixel+='10'
else:
pixel+='11'
return int(pixel,2)
def DNA_XOR(base1,base2):
#转成整数进行异或
pixel=DNA_Decode(base1,'AGCT')^DNA_Decode(base2,'AGCT')
return DNA_Encode(pixel,'AGCT')
def main():
#原始图像路径
img_path='./lena512color.tiff'
#加密密钥参数列表
key=[0.123456789010,0.234578900,0.3456789012,0.245789012,0.4567890124,0.5678901234,0.6789012346,0.7890123456,0.6890123450]
new_key=Generate_Key(img_path,key)
#原始图像
img=cv2.imread(img_path)[:,:,(2,1,0)]
#加密后的图像
img_encrypt=encrypt(img_path,new_key)
cv2.imwrite('./lena512color_encrypt.tiff',img_encrypt)
decrypt_path='./lena512color_encrypt.tiff'
#正确密钥解密图像
img_decrypt=decrypt(decrypt_path,new_key)
#错误密钥解密图像
wrong_key=list(new_key)
wrong_key[8]+=pow(10,-10)
wrong_decrypt=decrypt(decrypt_path,wrong_key)
#结果展示
plt.rcParams['font.sans-serif'] = ['SimHei'] # 中文乱码
#子图1,原始图像
plt.subplot(221)
#imshow()对图像进行处理,画出图像,show()进行图像显示
plt.imshow(img)
plt.title('原始图像')
#不显示坐标轴
plt.axis('off')
#子图2,加密后图像
plt.subplot(222)
plt.imshow(img_encrypt)
plt.title('加密图像\nq0={}'.format(new_key[8]))
plt.axis('off')
#子图3,错误密钥解密结果
plt.subplot(223)
plt.imshow(wrong_decrypt)
plt.title('解密图像\nq0={}'.format(wrong_key[8]))
plt.axis('off')
#子图4,正确密钥解密结果
plt.subplot(224)
plt.imshow(img_decrypt)
plt.title('解密图像\nq0={}'.format(new_key[8]))
plt.axis('off')
# #设置子图默认的间距
plt.tight_layout()
#显示图像
plt.show()
if __name__ == '__main__':
main()
扩展
NPCR
像素数变化率(NPCR)和统一平均变化强度(UACI)。NPCR和UACI分别表示两张加密图像之间的变化像素数和两张加密图像之间的平均变化强度数。NPCR和UACI的理想值为99.61%和33.46%
疑问
仔细阅读论文并进行实验时,发现了一些问题(不排除是自己理解错了🙄)
Table1 八种碱基配对规则???
感觉这个表有点不太对,它这样八种规则不是一样吗???不都是00-A;01-C;10-G;11-T吗???
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 00-A | 01-C | 10-G | 11-T | 01-C | 00-A | 11-T | 10-G |
| 01-C | 00-A | 11-T | 01-C | 11-T | 10-G | 10-G | 00-A |
| 10-G | 11-T | 00-A | 10-G | 00-A | 01-C | 01-C | 11-T |
| 11-T | 10-G | 01-C | 00-A | 10-G | 11-T | 00-A | 01-C |
我认为正确的八种规则如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 00-A | 00-C | 00-G | 00-T | 00-C | 00-A | 00-T | 00-G |
| 01-C | 01-A | 01-T | 01-C | 01-T | 01-G | 01-G | 01-A |
| 10-G | 10-T | 10-A | 10-G | 10-A | 10-C | 10-C | 10-T |
| 11-T | 11-G | 11-C | 11-A | 11-G | 11-T | 11-A | 11-C |
生成初始值—SHA-256???
d = h e x 2 d e c ( d ) / 2 42 d = hex2dec(d)/2^{42} d=hex2dec(d)/242
我觉得这个公式除数的幂不对,应为38即 d = h e x 2 d e c ( d ) / 2 38 d = hex2dec(d)/2^{38} d=hex2dec(d)/238
因为SHA-256消息摘要256位,第一部分分8块,每块7个16进制数,也就是每块28bits转换成浮点小数 m j ∈ ( 0 , 0.0156 ) m_j∈(0, 0.0156) mj∈(0,0.0156) 公式 m j = h e x 2 d e c ( m 1 , . . . , m 8 ) / 2 34 m_j = hex2dec(m_1,..., m_8)/2^{34} mj=hex2dec(m1,...,m8)/234 这是没错的(每块最大数字为 2 28 , 2 28 / 2 34 = 0.015625 2^{28},2^{28}/2^{34}=0.015625 228,228/234=0.015625 );那么第二部分剩下8个16进制数,也就是32位,虽然比第一部分的块多了一个16进制数,但一个十六进制数是4bits,所以转成小数公式应为 d = h e x 2 d e c ( d ) / 2 38 d = hex2dec(d)/2^{38} d=hex2dec(d)/238。
解密???
在加密图像过程中使用SHA-256算法修改了混沌系统的初始条件和控制参数,增强了加密过程和明文图像的相关性,提高了安全性。但是这就产生了一个问题,安全性太高了,搞得加密图像自己也难以解密了,因为无法根据加密后的图像得知修改后的混沌系统的初始值,原论文有问题???也许是加密图像传输过程中密钥也一起传输,这样不是更不安全吗???
答:通过长时间思考以及询问,密钥应该是在传输过程中随密文一起传输的,至于怎么传输就不在本研究范围内了。😜