随机变量
- 定义:随机变量(random variable)表示随机现象(在一定条件下,并不总是出现相同结果的现象称为随机现象)中各种结果的实质函数(一切可能的样本点)。例如某一时间内公共汽车站等车的人数,电话交换台在一定时间内收到的呼叫次数。
- 详细解析:随机变量就是一个随机的数,它是对任何的“随机的东西”做的量化。下面我们对随机和量化做解释:
- 随机的对象可以是任何东西:明天的天气是晴、阴、雨,扔硬币的结果可以是正面或者反面,这些结果并未用数字刻画。
- 我们借助概率论来研究它们,因此我们要使用数学语言,于是我们可以把晴、阴、雨贴上标签,叫做0、1、2;然后把明天的天气状况用一个字母X来表示,于是“明天下雨”就变成了“X=2”。这样,这个原本没有数学描述的随机结果就变成了一个可能的取值为0、1、2的随机数,我们称之为随机变量。
- 总之,你把随机现象的种种可能性都用数字表达出来,并用一套数学语言描述,这就是随机变量。
随机过程
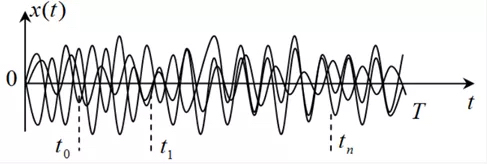
- 定义:随机过程是一组时间函数的集合,随机过程的每个样本函数(一个随机信号)是一个确定的时间函数x(t)(t = 0~T)。
- 详细解析: 从信号分析的角度看,一个随机过程就是针对一个实验测量无数个样本,每一个样本就是一个随机信号(且所有样本测量的时间都是0-T),以 X(t) 表示;然后我们把这些样本摆放如下:
我们从两个角度描述这个图像:
- 从纵向看,一个random process是你针对某个任务进行测量的所有样本信号的集合。
- 从横向的角度,任意切一刀,你会看到所有你测量的样本信号在这个时刻的幅度值都不一样,它们是随机的(我们从中随机挑选一个),为了表征这些幅度值的统计特性,我们用random variable来表征,0-T中间有无数个random variable(相当于你切了无数刀),这些无数个随机变量的集合就是随机过程。
- 个人理解为:若对0-T天的天气进行预测
- 将0-T天所有可能结果以向量结果存储(这时每个向量的结果都是已知的),并同时摆放即相当于从纵向看。
- 将每一天的预测结果视作一个随机变量,将这些随机变量依次放到一个集合即相当于从横向看。