数据结构与算法引入
我们都知道数据结构与算法很重要,甚至会将其称为程序员的“内功”,但是我们花了很多时间学的算法和数据结构,好像就只是为了应对算法面试,对日常的开发工作没有什么帮助。
这点对于我们数据工程师来说,体感更甚——平时工作看起来主要是写SQL(甚至会被戏称SQL boy),算法就像是只存在于那些开箱即用的数据处理工具中而已,和我们的日常开发完全没什么关系。
但实际上,这只是因为时代浪花下,大数据领域还在成长期的自然现象。业务快速迭代时期,对于成本和效率看的不是很重,全靠平台架构的能力兜底,对于数据工程师来说,做好业务需求实现就行。
随着大数据领域的成熟,企业也都减缓了快速扩张的脚步,因此最近几年我们听的最多的一个词就是——降本增效。
现在对于数据工程师来说,不但要完成业务需求,还需要能够保质保量,高效产出。
这就需要掌握大数据基础知识,学好数据结构和算法,并且在生产实践中选择最合适的方案去落地。这也是很多早期进入大数据行业的小伙伴,逐步被淘汰的根本原因。
由于数据结构与算法经典书籍与教程太多了,我这里推荐《剑指Offer(专项突破版):数据
结构与算法名企面试题精讲》和《数据结构与算法图解》(杰伊·温格罗)两本书。
数据结构与算法面试专题,则是针对数据开发面试与工作中所必备的数据结构与算法知识进行讲解。
归并排序基础
- 题目1:归并排序递归版
- 题目2:归并排序递归非递归版
介绍
归并排序(Merge Sort)是建立在归并操作上的一种有效的排序算法。
该算法是采用分治法(Divide and Conquer)的一个非常典型的应用,需要额外空间作为代价。
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。二路归并排序就是两两排序,然后两个区域一起排序,以此类推。
归并排序是稳定的。因为在使用额外空间的时候,靠前区域的元素只要小于等于靠后区域的元素就能被放进额外空间。
其实现原理如下:
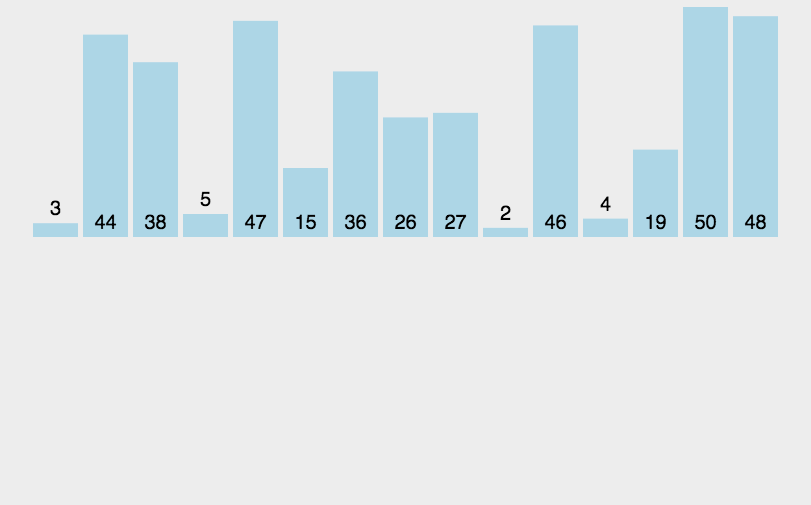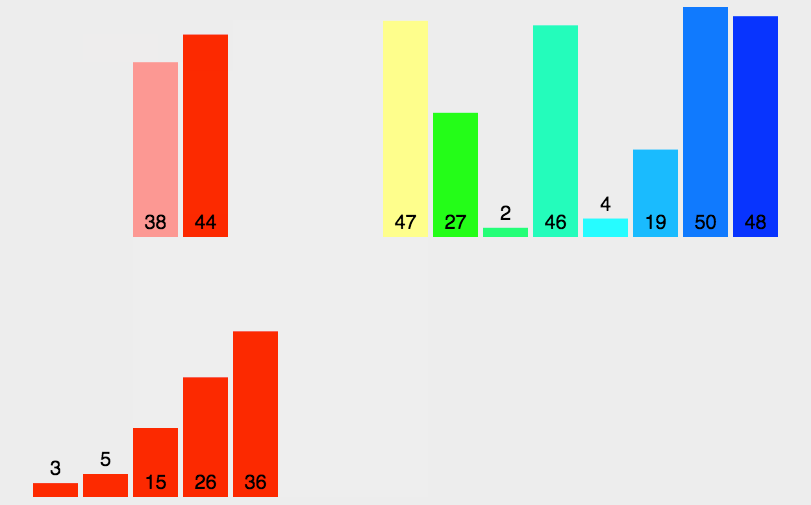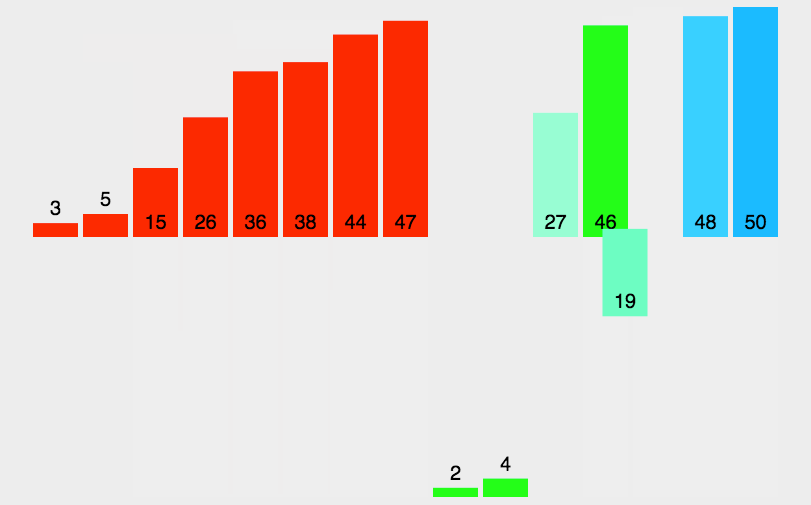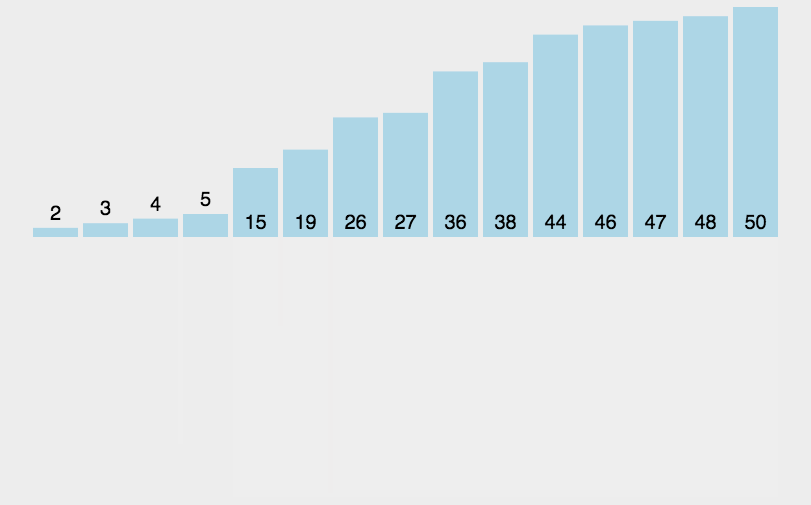
- 首先,将待排序的数组不断地分成两半,直到每个子数组只有一个元素(一个元素本身就是有序的)。
- 然后,对划分后的子数组进行合并。合并的过程是比较两个已排序子数组的元素,将较小的元素依次放入一个新的辅助数组中,直到其中一个子数组的元素全部放入辅助数组,再将另一个子数组剩余的元素直接复制到辅助数组的后面。
- 最后,将辅助数组中的已排序元素复制回原数组对应的位置。
- 通过不断地对子数组进行分割和合并操作,最终整个数组就会被排序。
归并排序的平均时间复杂度、最坏时间复杂度和最好时间复杂度均为 O (nlogn),空间复杂度为 O (n)。它是一种稳定的排序算法,即相同元素的相对顺序在排序前后保持不变。
题目1:归并排序递归版
整体是通过递归实现:左边排好序+右边排好序+merge让整体有序(借助外部数组实现)
// 归并排序(递归版)
public void mergeSort(int[] arr) {
// 临界值判断
if (arr == null || arr.length < 2) {
// 企业开发最好抛出异常,避免异常数据流向下游,无法及时监控
// throw new IllegalArgumentException("数组为空");
return;
}
mergeSort(arr, 0, arr.length - 1);
}
private void mergeSort(int[] arr, int l, int r) {
if (l >= r) {
return;
}
// 防止出现越界
int m = l + ((r - l) >> 1);
// 通过递归,直线左边和右边都有序
mergeSort(arr, l, m);
mergeSort(arr, m + 1, r);
// 归并处理
mergeSort(arr, l, m, r);
}
private void mergeSort(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];
int i = 0;
// 设置左右两个指针
int p1 = l;
int p2 = m + 1;
while (p1 <= m && p2 <= r) {
help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
}
// 要么p1越界,要么p2越界
while (p1 <= m) {
help[i++] = arr[p1++];
}
while (p2 <= r) {
help[i++] = arr[p2++];
}
for (int j = 0; j < help.length; j++) {
arr[l + j] = help[j];
}
}题目2:归并排序非递归版
非递归的实现核心,在于折腾“步长”这个概念,
- 从步长 = 1 开始,步长的变化一定是2的某次方
- 最后一步,如果凑不齐左组就不管了, 右组有多少算多少
- 步长一旦超过总长度,就说明搞完了
// 归并排序(非递归版)
public void mergeSort(int[] arr) {
// 临界值判断
if (arr == null || arr.length < 2) {
return;
}
// 步长
int batch = 1;
int size = arr.length;
while (batch < size) {
int l = 0;
while (l < size) {
int m = 0;
if (size - l >= batch) {
m = l + batch - 1;
} else {
break;
}
int r = Math.min(size - 1, m + batch);
mergeSort(arr, l, m, r);
if (r == size - 1) {
break;
} else {
l = r + 1;
}
}
if (batch > size / 2) {
break;
}
batch <<= 1;
}
}
private void mergeSort(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];
int i = 0;
// 设置左右两个指针
int p1 = l;
int p2 = m + 1;
while (p1 <= m && p2 <= r) {
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
// 要么p1越界,要么p2越界
while (p1 <= m) {
help[i++] = arr[p1++];
}
while (p2 <= r) {
help[i++] = arr[p2++];
}
for (int j = 0; j < help.length; j++) {
arr[l + j] = help[j];
}
}归并排序拓展
仅仅掌握归并排序的基础实现是不够的,还需要掌握如何利用它的思路去解决新的类似的问题,本文以几个拓展题为例子,带大家拓展一下。
- 题目1:求数组小和
- 题目2:求数组中的逆序对数量
- 题目3:求数组中的大两倍数对数量
- 题目4:区间和达标的子数组数量
题目1:求数组小和
题目介绍
在一个数组中,一个数左边比它小的数的总和,叫数的小和,所有数的小和累加起来,叫数组小和。求数组小和。
例子:
[1,3,4,2,5]1左边比1小的数:没有
3左边比3小的数:1
4左边比4小的数:1、3
2左边比2小的数:1
5左边比5小的数:1、3、4、 2
所以数组的小和为1+1+3+1+1+3+4+2=16
实现代码
利用归并排序的特点,在归并排序过程中,不断去找每个数右边有多少个数比它大,那对应数在小和里就应该有多少个。
public int smallSum(int[] arr) {
if (arr == null || arr.length < 1) {
return 0;
}
return smallSum(arr, 0, arr.length - 1);
}
private int smallSum(int[] arr, int l, int r) {
if (l == r) {
return 0;
}
int m = l + ((r - l) >> 1);
return smallSum(arr, l, m) + smallSum(arr, l, m) + smallSum(arr, l, m, r);
}
private int smallSum(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];
int i = 0;
int p1 = l;
int p2 = m + 1;
int res = 0;
while (p1 <= m && p2 <= r) {
if (arr[p1] < arr[p2]) {
res += (r - p2 + 1) * arr[p1];
help[i++] = arr[p1++];
} else {
help[i++] = arr[p2++];
}
}
while (p1 <= m) {
help[i++] = arr[p1++];
}
while (p2 <= r) {
help[i++] = arr[p2++];
}
for (int j = 0; j < help.length; j++) {
arr[l + j] = help[j];
}
return res;
}题目2:求数组中的逆序对数量
题目介绍
在一个数组中,任何一个前面的数a,和任何一个后面的数b,如果(a,b)是降序的,就称为逆序对, 返回数组中所有的逆序对。
实现代码
和上一题思路类似,不过是逆序。需要从右往左Merge,相等的时候先拷贝右边的。
public int reversePairSum(int[] arr) {
if (arr == null || arr.length < 1) {
return 0;
}
return reversePairSum(arr, 0, arr.length - 1);
}
private int reversePairSum(int[] arr, int l, int r) {
if (l == r) {
return 0;
}
int m = l + ((r - l) >> 1);
return reversePairSum(arr, l, m) + reversePairSum(arr, l, m) + reversePairSum(arr, l, m, r);
}
private int reversePairSum(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];
int i = 0;
// 逆序处理
int p1 = m;
int p2 = r;
int res = 0;
while (p1 >= l && p2 > m) {
if (arr[p1] > arr[p2]) {
res += p2 - m;
help[i--] = arr[p1--];
} else {
help[i--] = arr[p2--];
}
}
while (p1 >= l) {
help[i--] = arr[p1--];
}
while (p2 <= r) {
help[i--] = arr[p2--];
}
for (int j = 0; j < help.length; j++) {
arr[l + j] = help[j];
}
return res;
}题目3:求数组中的大两倍数对数量
题目介绍
在一个数组中,对于每个数num,求有多少个后面的数 * 2 依然<num,求总个数
比如:[3,1,7,0,2]
3的后面有:1,0
1的后面有:0
7的后面有:0,2
0的后面没有
2的后面没有
所以总共有5个
实现代码
也是类似的思想,因为merge的时候,划分出来的[l,m] 和 [m+1,r]块中是能保证有序的,就可以拿左边的依次去和右边比较来实现。
public int biggerTwice(int[] arr) {
if (arr == null || arr.length < 1) {
return 0;
}
return biggerTwice(arr, 0, arr.length - 1);
}
private int biggerTwice(int[] arr, int l, int r) {
if (l == r) {
return 0;
}
int m = l + ((r - l) >> 1);
return biggerTwice(arr, l, m) + biggerTwice(arr, l, m) + biggerTwice(arr, l, m, r);
}
private int biggerTwice(int[] arr, int l, int m, int r) {
// [l,m] [m+1,r]
int res = 0;
// 目前囊括进来的数,是从[m+1, windowR)
int windowR = m + 1;
for (int i = l; i <= m; i++) {
while (windowR <= r && arr[i] > (arr[windowR] * 2)) {
windowR++;
}
res += windowR - m - 1;
}
int[] help = new int[r - l + 1];
int i = 0;
int p1 = l;
int p2 = m + 1;
while (p1 <= m && p2 <= r) {
help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= m) {
help[i++] = arr[p1++];
}
while (p2 <= r) {
help[i++] = arr[p2++];
}
for (int j = 0; j < help.length; j++) {
arr[l + j] = help[j];
}
return res;
}题目4:区间和达标的子数组数量
题目介绍
给定一个数组arr,和两个整数a和b(a<=b),求arr中有多少个子数组,累加和在[a,b]这个范围上,返回达标的子数组数量
实现代码
这个在归并的基础上,还需要借助前缀和数组来实现。
public int countRangeSum(int[] arr,int lower,int upper){
if (arr==null || arr.length<1){
return 0;
}
long[] preSum = getPreSum(arr);
return countRangeSum(preSum,0,arr.length-1,lower,upper);
}
// 获取前缀和数组
// 为了避免累加后越界,改用long存储
private long[] getPreSum(int[] arr){
long[] res = new long[arr.length];
res[0]= arr[0];
for (int i = 1; i < res.length; i++) {
res[i]=arr[i]+res[i-1];
}
return res;
}
private int countRangeSum(long[] preSum, int l, int r, int lower, int upper) {
// 临界情况判断处理
if (l==r){
return preSum[l]>=lower && preSum[l]<=upper ? 1:0;
}
int m = l +((r-l)>>1);
return countRangeSum(preSum,l,m,lower,upper) + countRangeSum(preSum,m+1,r,lower,upper)
+countRangeSum(preSum,l,m,r,lower,upper);
}
private int countRangeSum(long[] preSum, int l, int m, int r, int lower, int upper) {
int res =0;
// 通过左右两个窗口去获取以当前数结尾,有多少子数组是满足需求的
int windowL=l;
int windowR=l;
// [windowL,windowR)
for (int i = m+1; i <=r ; i++) {
// 获取以当前数结尾,所需要的前面子数组和应该在什么范围才能满足需求
long min = preSum[i]-upper;
long max = preSum[i]-lower;
while (windowR<=m && preSum[windowR]<=max){
windowR++;
}
while (windowL<=m && preSum[windowL]<min){
windowL++;
}
res += windowR-windowL;
}
long[] help = new long[r - l + 1];
int i = 0;
int p1 = l;
int p2 = m + 1;
while (p1 <= m && p2 <= r) {
help[i++] = preSum[p1] <= preSum[p2] ? preSum[p1++] : preSum[p2++];
}
while (p1 <= m) {
help[i++] = preSum[p1++];
}
while (p2 <= r) {
help[i++] = preSum[p2++];
}
for (int j = 0; j < help.length; j++) {
preSum[l + j] = help[j];
}
return res;
}