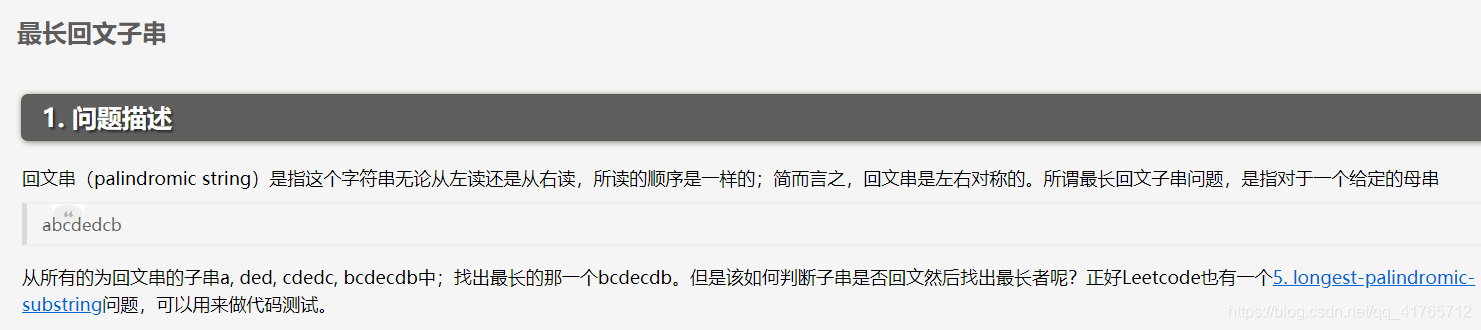
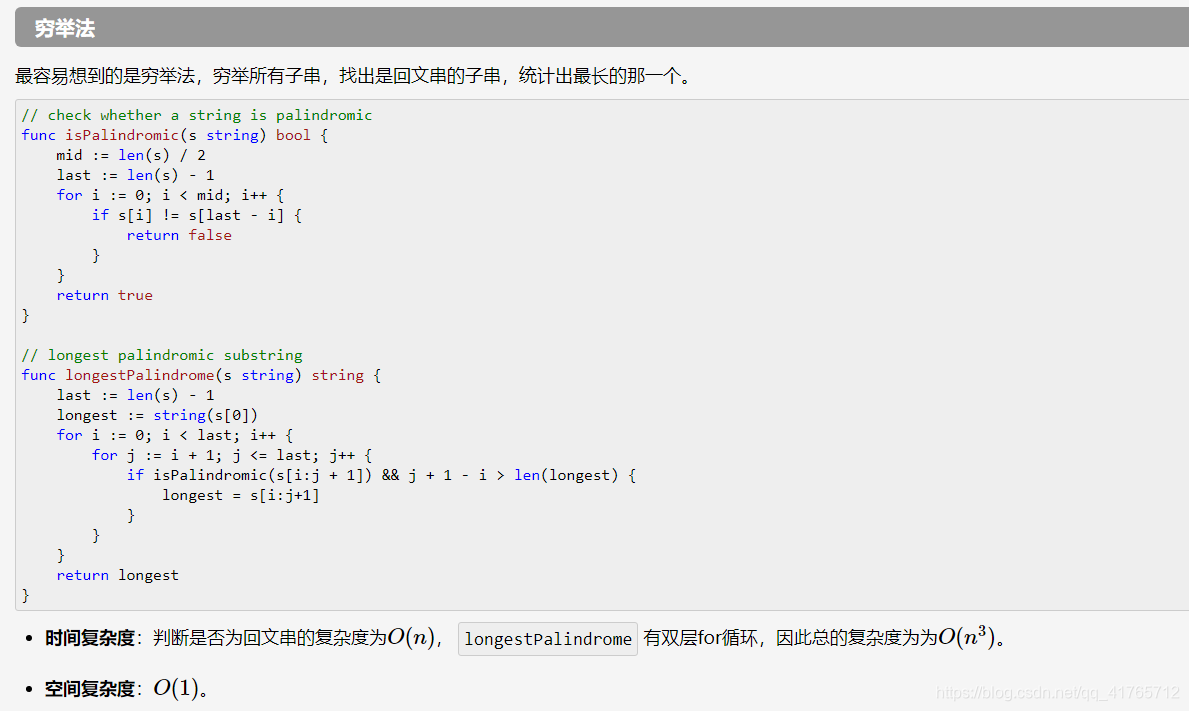
2.动态规划

dp[i][j]表示“以s[i]开始s[j]结尾的回文串的长度。如果这个字符串不是回文串，让dp[i][j]=0”。显然，j>=i，只需往dp填j>=i的部分即可。

dp[i][j]的递推公式可以这么表述：

（1）首先对dp的对角线元素初始化为1，也就是当i==j时，dp[i][j]=1。

这很显然，每个单独的字符其实就是个长度为1的回文串。

（2）当j-i==1：

若s[i]==s[j]，则dp[i][j]=2；否则dp[i][j]=0。

解释：当j-i==1时，若s[i]==s[j]，则s[i]和s[j]可以组成一个长度为2的回文串。若s[i]！=s[j]，显然他们不可能组成回文串，dp[i][j]=0。

（3）当j-i>=2：

若s[i]==s[j]：若dp[i+1][j-1]>0，则dp[i][j]= dp[i + 1][j - 1] + 2;否则dp[i][j]= 0;

若s[i]！=s[j]：dp[i][j]=0。

解释：如果s[i]==s[j]，表明这个子串有可能是回文串。当去头去尾后它是回文串时，就可以在去头去尾的那个回文串长度基础上+2，得到它的长度。如果去头去尾后不是回文串，那这个子串一定不是回文串，回文串长度只能是0。

若s[i]！=s[j]，显然他们不可能组成回文串，dp[i][j]=0。

只需找到dp[i][j]的最大元素和它对应的i和j就可以得到结果“s中最长回文子串”。

public class Main {
    public static void main(String[] args) {
        String s = "";
        String l = longestPalindrome(s);
        System.out.println(l);
    }

    public static String longestPalindrome(String s) {
        int len = s.length();
        int[][] dp = new int[len+10][len+10];//值代表最长回文
        char[] str = s.toCharArray();
        int max = 1, start = 0;
        if(s.isEmpty()){
            return "";
        }
        //一个字符初始化
        for (int i = 0; i < len; i++) {
            dp[i][i] = 1;
        }
        //相邻元素
        for (int i = 0; i < len-1; i++) {
            if (str[i] == str[i + 1]) {
                dp[i][i + 1] = 2;
                max=2;
                start=i;
            } else {
                dp[i][i + 1] = 0;
            }
        }
        //相隔一个至少元素
        //动态规划需要注意如何从低向上遍历，及i,j之间的关系-------参考矩阵连乘
        for (int k = 2; k < len; k++) {//子串长度
            for (int i = 0; i + k < len; i++) //子串开始位置
            {
                int j = i + k;//子串结束位置
                if (str[i] == str[j]&&dp[i + 1][j - 1]>=1) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                }else{
                    dp[i][j]=0;

                }
                if(max<dp[i][j]){
                    max=dp[i][j];
                    start=i;
                }
            }
        }
        System.out.println(max);
        System.out.println(start);
        return s.substring(start,start+max);
    }
}

分治