首先明确：

1. KMP模式匹配算法的目的是：快速在主串中匹配到子串；
2. KMP算法达到的效果是消除了主串指针的回溯，提高了字符串的匹配效率。

一、BF匹配算法存在的问题

既然KMP算法是一种优化算法，那肯定原算法有不足之处。
BF算法是最基础的匹配算法，它的思想是：对于主串的每一个字符，当做子串的开头字符进行一次匹配，直到完全匹配成功。

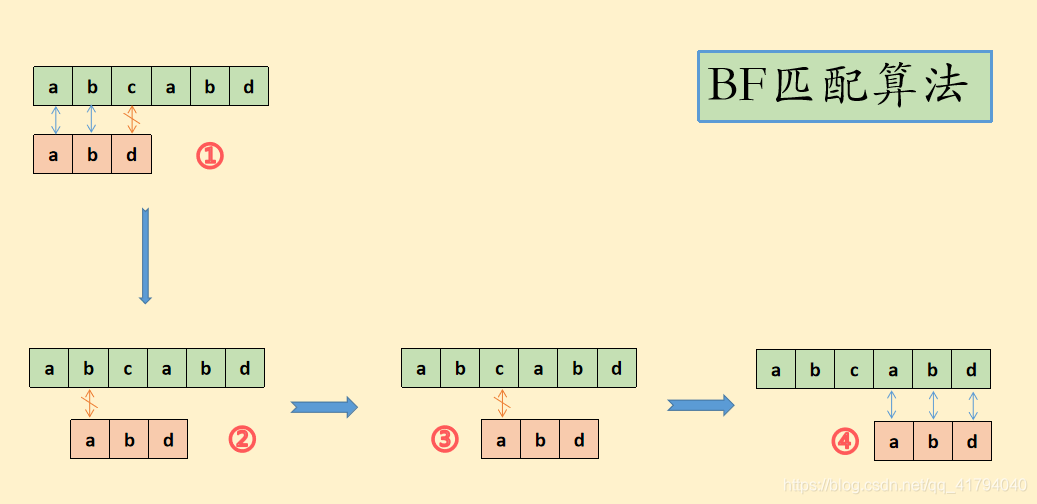
它的不足之处在于，当不完全匹配发生，再次进行匹配时可能出现主串指针回溯的现象，可以看下图的例子：

规定主串为S[n]，子串为T[n]，则有：

• 在①中，S[0]=T[0]，S[1]=T[1]，S[2]≠T[2]，匹配不完全，此时主串匹配指针位于S[2]处。
• 在②中，由于要从主串的第二个字符开始重新检验匹配，故主串匹配指针回溯至S[1]，仍不匹配。
• …
• 到④时，S[3]=T[0]，S[4]=T[1]，S[5]=T[2]，完全匹配。

二、KMP匹配算法

KMP算法能够消除主串指针的回溯，只通过移动子串来进行多次匹配。
KMP算法能够高效的发挥作用有两个前提条件：

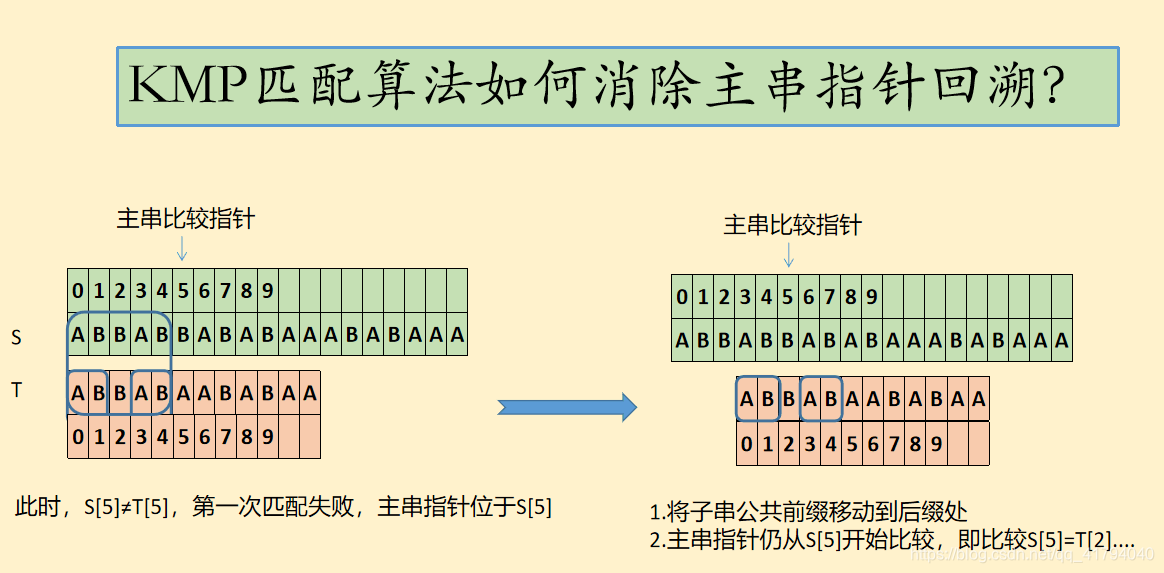
在满足以上条件时，KMP算法可以在遇到不完全匹配的情况下，高效地避免主串指针回溯带来的效率损失，可以看以下例子：

其实简单说原理，就是：
1.假设在某处主串与子串的字符不同，但之前部分完全匹配。
2.子串中存在公共的前后缀（则由1知主串中也存在），因此移动子串的实质是将子串的公共前缀，与主串的公共后缀对齐，从而避免了子串从主串S[1]、S[2]处重新判断，消除了指针的回溯.
3.那为什么可以直接将子串移动，让子串T[0]从主串S[3]开始比较？会不会遗漏掉从S[1]、S[2]处完全匹配的情况？不会。因为我们移动前选的是主串、子串公共部分的最长公共前后缀。

因此，当主串和子串间在存在较多“部分匹配”的前提下，KMP算法具有提高效率的作用；而当它们之间共同部分较少时，则跟BF算法的效率差异不大。

个人理解是目前这样，欢迎讨论~